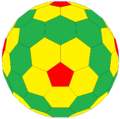
е…ӯи§’еҢ–дә”и§’еҢ–еҖ’и§’еҚҒдәҢйқўй«”
еңЁе№ҫдҪ•еӯёдёӯпјҢе…ӯи§’еҢ–дә”и§’еҢ–еҖ’и§’еҚҒдәҢйқўй«”жҳҜдёҖзЁ®еҮёеӨҡйқўй«”пјҢдё”еұ¬ж–јдёүи§’йқўеӨҡйқўй«”пјҢд№ҚзңӢд№ӢдёӢеғҸжҳҜз”ұжӯЈдёүи§’еҪўзө„жҲҗпјҢдҪҶеҜҰйҡӣдёҠе®ғжҳҜз”ұеӨҡзЁ®дёҚеҗҢзҡ„дёҚзӯүйӮҠдёүи§’еҪўжүҖзө„жҲҗгҖӮ жҖ§иіӘе…ӯи§’еҢ–дә”и§’еҢ–еҖ’и§’еҚҒдәҢйқўй«”еҸҜд»Ҙз”ұжҲӘи§’иҸұеҪўдёүеҚҒйқўй«”еңЁжҜҸеҖӢйқўеҠ дёҠйҢҗй«”пјҲKleetopeпјүпјҢжҺҘйҢҗй«”зҡ„й«ҳзӮәйқўеҲ°еӨ–жҺҘзҗғзҡ„жңҖй•·и·қйӣўжүҖзө„жҲҗзҡ„еӨҡйқўй«”пјҢеӣ жӯӨпјҢе…ӯи§’еҢ–дә”и§’еҢ–еҖ’и§’еҚҒдәҢйқўй«”дәҰеұ¬ж–јеә·еЁҒеӨҡйқўй«”гҖӮ е…ӯи§’еҢ–дә”и§’еҢ–еҖ’и§’еҚҒдәҢйқўй«”е…ұжңү240еҖӢйқўгҖҒ360еҖӢйӮҠгҖҒе’Ң122еҖӢй Ӯй»һпјҢз”ұж–је…¶зӮәеҮёеӨҡйқўй«”пјҢдё”жІ’жңүз ҙжҙһпјҢеӣ жӯӨжӯҗжӢүзӨәжҖ§ж•ёдёҖжЁЈжҳҜ2гҖӮ жӯ·еҸІе…ӯи§’еҢ–дә”и§’еҢ–еҖ’и§’еҚҒдәҢйқўй«”зӮәеҜҢеӢ’жҸҗеҮәзҡ„з¶Іж јзҗғй Ӯд№ӢдёҖпјҢдё”ж–ј1954е№ҙ6жңҲз”іи«Ӣе°ҲеҲ©зҚІеҮҶ[1][2]пјҢиҖҢеҫһзҚІеҮҶеҫҢе°ҲеҲ©з”ҹж•Ҳзҡ„17е№ҙе…§е»әйҖ зҡ„д»»дҪ•дёҖзЁ®з¶Іж јзҗғй ӮжҲ–е…ӯи§’еҢ–дә”и§’еҢ–еҖ’и§’еҚҒдәҢйқўй«”еҪўзӢҖжҲ–зөҗж§Ӣзҡ„е»әзҜүзү©йғҪиҰҒж”Ҝд»ҳеҜҢеӢ’е°ҲеҲ©ж¬ҠзЁ…[2]пјҢдҪҶеҜҰйҡӣдёҠпјҢи©Із¶Іж јзҡ„иЁӯиЁҲиҲҮBauersfeldзҡ„зӣёеҗҢгҖӮ[3] жӯӨеӨ–пјҢеҜҢеӢ’жҸҗеҲ°пјҢиҰҒж§ӢйҖ йҖҷеҖӢеӨҡйқўй«”иҰҒеҫһжӯЈдәҢеҚҒйқўй«”й–Ӣе§ӢпјҢе°ҮжҜҸеҖӢйқўеҲҶеҖӢжҲҗиӢҘе№ІеҖӢе…Ёзӯүзҡ„жӯЈдёүи§’еҪўпјҢеҶҚе°ҮйҖҷдәӣй Ӯй»һжҠ•еҪұеңЁдёҖеҖӢзҗғйқўдёҠпјҢеҶҚе°Үж–°зҡ„й Ӯй»һж§ӢйҖ жҲҗдёҖеҖӢеӨҡйқўй«”е°ұжңғи®ҠжҲҗйҖҷдёҖеҖӢеӨҡйқўй«”пјҢ當然пјҢдёүи§’еҪўдёҚеҶҚжҳҜзӯүйӮҠзҡ„гҖӮиӢҘеҶҚе°Үй Ӯй»һжҲӘеҺ»пјҢе°ұи®ҠжҲҗдәҶжҲӘи§’е…ӯи§’еҢ–дә”и§’еҢ–еҖ’и§’еҚҒдәҢйқўй«”пјҢжӯӨжҷӮпјҢе…¶зөҗж§Ӣе°ұжӣҙжҺҘиҝ‘зҗғй«”пјҢжҖ§иіӘд№ҹжӣҙзӮәжҺҘиҝ‘зҗғзҡ„зү№жҖ§дәҶгҖӮ[4] 1960е№ҙпјҢеҜҢеӢ’жҸҸиҝ°дәҶиӢҘиҰҒе»әз«ӢдёҖеҖӢе·ЁеһӢе…ӯи§’еҢ–дә”и§’еҢ–еҖ’и§’еҚҒдәҢйқўй«”й«”е»әзҜүзү©зҡ„еҸҜиЎҢжҖ§пјҢд»–жҸҗеҲ°пјҡз”ұ16еҸ°еӨ§еһӢеЎһиҖғж–ҜеҹәзӣҙеҚҮж©ҹзө„жҲҗзҡ„йЈӣиЎҢйҡҠеҸҜеңЁдёүеҖӢжңҲе…§е®ҢжҲҗ1.6е…¬йҮҢй«ҳгҖҒ3е…¬йҮҢеҜ¬зҡ„еҚҠзҗғпјҢиҠұиІ»жҳҜе…©е„„зҫҺе…ғпјҢдёҰиғҪж¶өи“Ӣ50еҖӢиЎ—еҚҖпјҢйҳІжӯўйӣӘиҗҪеңЁеұӢеӯҗдёҠпјҢдёҰжҺ§еҲ¶ж—Ҙе…үзҡ„еҪұйҹҝе’Ңз©әж°Је“ҒиіӘгҖӮ[2] ең–еғҸ
еҸғе»әеҸғиҖғж–ҮзҚ»
|
||||||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia