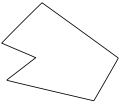
ه‡¹ه‡¸و€§ (ه¹¾ن½•)هœ¨ه‡ ن½•ه¦ن¸ï¼Œن¸€ن¸ھه¹¾ن½•هœ–ه½¢هڈ¯هˆ†ن¸؛ه‡¸وˆ–ه‡¹çڑ„م€‚ن¾‹ه¦‚ه¤ڑé‚ٹه½¢ه’Œه¤ڑé¢é«”م€‚ه…¶ن¸ï¼Œه‡¸çڑ„ه¤ڑé‚ٹه½¢ç¨±ç‚؛ه‡¸ه¤ڑé‚ٹه½¢م€په‡¹çڑ„ه¤ڑé‚ٹه½¢ه‰‡هڈ¯ç¨±ç‚؛ه‡¹ه¤ڑé‚ٹه½¢وˆ–éه‡¸ه¤ڑé‚ٹه½¢ï¼Œه¤ڑé¢é«”與ه¤ڑèƒé«”ن؛¦ç„¶م€‚然而هœ¨ن¸‰ç¶وˆ–و›´é«کç¶ه؛¦çڑ„ç©؛é–“ن¸ï¼Œن¸چوک¯ه‡¸çڑ„ه¹¾ن½•هœ–ه½¢ن¸چن¸€ه®ڑوœƒوک¯ه‡¹ه¹¾ن½•هœ–ه½¢ï¼Œن؛¦هڈ¯èƒ½وک¯وکںه½¢ه¹¾ن½•هœ–ه½¢ï¼Œه› و¤هœ¨ن¸‰ç¶وˆ–و›´é«کç¶ه؛¦çڑ„ç©؛é–“ن¸è¼ƒه¸¸هˆ†ç‚؛ه‡¸èˆ‡éه‡¸م€‚ ه‡¸ه¹¾ن½•هœ–ه½¢ه‡¸ه¹¾ن½•هœ–ه½¢وک¯وŒ‡ه†…部ن¸؛ه‡¸é›†çڑ„ه¹¾ن½•هœ–ه½¢[1],ن؛Œç¶ç©؛é–“ن¸çڑ„ه‡¸ه¹¾ن½•هœ–ه½¢ç¨±ç‚؛ه‡¸ه¤ڑé‚ٹه½¢م€پن¸‰ç¶ç©؛é–“ه‰‡ç¨±ه‡¸ه¤ڑé¢é«”م€‚è‹¥ن¸€ه¤ڑèƒه½¢çڑ„ه†…部ن¸؛ه‡¸é›†ï¼Œه‰‡ç¨±ه‡¸ه¤ڑèƒه½¢م€‚ ن؛Œç¶ç©؛é–“ن¸çڑ„ه‡¸ه¹¾ن½•هœ–ه½¢ç¨±ç‚؛ه‡¸ه¤ڑé‚ٹه½¢ï¼Œç®€هچ•ه¤ڑè¾¹ه½¢çڑ„ن¸‹هˆ—و€§è´¨ن¸ژه…¶ه‡¸و€§ç‰ن»·ï¼ڑ ه‡¸ه¹¾ن½•هœ–ه½¢çڑ„ه‡¸هŒ…與ه…¶é‚ٹ界相هگŒم€‚
ه‡¹ه¹¾ن½•هœ–ه½¢ه‡¹ه¹¾ن½•هœ–ه½¢وک¯وŒ‡ه†…部ن¸چوک¯ه‡¸é›†çڑ„ه¹¾ن½•هœ–ه½¢ï¼Œهœ¨ن؛Œç¶ç©؛é–“ن¸ï¼Œن¸چوک¯ه‡¸é›†çڑ„ç°،ه–®ه¤ڑé‚ٹه½¢ï¼Œç¨±ç‚؛ه‡¹ه¤ڑè¾¹ه½¢ï¼ˆConcave polygon)[2]وˆ–ه‡¹è§’[3]م€‚ ه‡¹ه¤ڑé‚ٹه½¢è‡³ه°‘هکهœ¨ن¸€ه€‹ه…§è§’ه¤§و–¼180ه؛¦م€‚ هœ¨ن¸‰ç¶ç©؛é–“ن¸ï¼Œن¸چوک¯ه‡¸çڑ„ه¹¾ن½•هœ–ه½¢ن¸چن¸€ه®ڑوœƒوک¯ه‡¹ه¹¾ن½•هœ–ه½¢ï¼Œن؛¦هڈ¯èƒ½وک¯وکںه½¢ه¤ڑé¢é«”,ه› و¤هœ¨ن¸‰ç¶ç©؛é–“ن¸è¼ƒه¸¸هˆ†ç‚؛ه‡¸èˆ‡éه‡¸م€‚
هڑ´و ¼ه‡¸èˆ‡éهڑ´و ¼ه‡¸ ه¦‚وœن¸€ن¸ھ简هچ•ه¤ڑè¾¹ه½¢çڑ„و¯ڈن¸ھه†…角ن¸¥و ¼ه°ڈن؛ژ180ه؛¦ï¼Œوک¯ن¸¥و ¼ه‡¸çڑ„ï¼›ه¦‚وœو¯ڈن¸ھé相邻é،¶ç‚¹é—´çڑ„ç؛؟و®µé™¤ç«¯ç‚¹ه¤–ن¸¥و ¼ن½چن؛ژه¤ڑè¾¹ه½¢çڑ„ه†…部,ن¹ںوک¯ن¸¥و ¼ه‡¸çڑ„م€‚ و‰€وœ‰é退هŒ–ن¸‰è§’ه½¢éƒ½وک¯ن¸¥و ¼ه‡¸çڑ„م€‚ وکںه½¢ه¹¾ن½•هœ–ه½¢وکںه½¢ه¹¾ن½•هœ–ه½¢وک¯éه‡¸ه¹¾ن½•هœ–ه½¢çڑ„ن¸€ه€‹ç‰¹ن¾‹ï¼Œه…¶ن¸¦وœھوœ‰ن¸€ه€‹وکژç¢؛çڑ„ه®ڑ義م€‚هœ¨ن؛Œç¶ç©؛é–“ن¸ï¼Œç¨±ç‚؛وکںه½¢ه¤ڑé‚ٹه½¢ï¼Œو•¸ه¸ه®¶Branko Grأ¼nbaumوŒ‡ه‡؛ن؛†ه…©ç¨®ç”±ه…‹و™®ه‹’وڈگه‡؛çڑ„ه®ڑ義ï¼ڑن¸€ç¨®وک¯ه…·وœ‰è‡ھ相ن؛¤ç¨œçڑ„و£وکںه½¢ه¤ڑé‚ٹه½¢ï¼Œن¸”è‡ھ相ن؛¤çڑ„稜ن¸چ產ç”ںو–°çڑ„é ‚é»ï¼Œهڈ¦ن¸€ç¨®وک¯é‚ٹهڈ¯éپçڑ„ç°،ه–®ه‡¹ه¤ڑé‚ٹه½¢[4]م€‚
هڈƒè¦‹هڈ‚考و–‡çŒ®
ه¤–部链وژ¥ |
Portal di Ensiklopedia Dunia