拉塞福散射

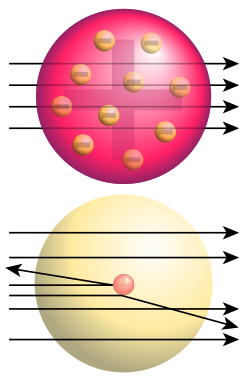
在原子物理學裏，拉塞福散射（英語：Rutherford scattering）指的是帶電粒子因為庫侖相對作用而進行的一種彈性散射（英语：elastic scattering）。這種散射實驗是由歐尼斯特·拉塞福領隊設計與研究，成功地於 1909 年證實在原子的中心有個原子核^[1]，也導致拉塞福模型的創立，及後來波耳模型的提出。應用拉塞福散射的技術與理論，拉塞福背散射（Rutherford backscattering）是一種專門分析材料的技術。拉塞福散射有時也被稱為庫侖散射，因為它涉及的位勢乃庫侖位勢。深度非弹性散射（deep inelastic scattering）也是一種類似的散射，在 60 年代，常用來探測原子核的內部。

α粒子散射的實驗完成于1909年。在那時代，原子被認為類比於梅子布丁（物理學家約瑟夫·湯姆森提出的，又稱葡萄乾布丁模型），負電荷（梅子）分散於正電荷的圓球（布丁）。假若這梅子布丁模型是正確的，由於正電荷完全散開，而不是集中於一個原子核，庫侖位勢的變化不會很大，通過這位勢的阿爾法粒子，其移動方向應該只會有小角度偏差。^[2][3]:51-53

在拉塞福的指導下，漢斯·蓋革和欧内斯特·马斯登發射α粒子射束來轟擊只有幾個原子厚度的薄金箔紙。^{[註 1]}然而，他們得到的實驗結果非常詭異，大約每8000個阿爾法粒子，就有一個粒子的移動方向會有很大角度的偏差（甚至超過 90°）；而其它粒子都直直地通過白金箔紙，偏差幾乎在2°到3°以內，甚至幾乎沒有偏差。從這結果，拉塞福斷定，大多數的質量和正電荷，都集中於一個很小的區域（這個區域後來被稱作“原子核”）；電子則包圍在區域的外面。當一個（正價）α粒子移動到非常接近原子核，它會被很強烈的排斥，以大角度反彈。原子核的小尺寸解釋了為什麼只有極少數的α粒子被這樣排斥。^[4][3]:51-53

拉塞福對這奇異的結果感到非常驚異。他後來常說：「這是我一生中最難以置信的事件…如同你用15吋巨砲朝著一張衛生紙射擊，而炮彈卻被反彈回來而打到你自己一般地難以置信。」^[2][3]:51-53

拉塞福計算出原子核的尺寸應該小於 ${\displaystyle 10^{-14}m\,\!}$ 。至於其具體的數值，拉塞福無法從這實驗決定出來。關於這一部份，請參閱後面的“原子核最大尺寸”一節。^[2]

拉塞福計算出來的微分截面是

${\displaystyle {\frac {d\sigma }{d\Omega }}=\left({\frac {qQ}{16\pi \epsilon _{0}E\sin ^{2}(\theta /2)}}\right)^{2}\,\!}$ ；

其中，${\displaystyle \sigma \,\!}$ 是截面，${\displaystyle \Omega \,\!}$ 是立體角，${\displaystyle q\,\!}$ 是阿爾法粒子的電荷量，${\displaystyle Q\,\!}$ 是散射體的電荷量，${\displaystyle \epsilon _{0}\,\!}$ 是真空電容率，${\displaystyle E\,\!}$ 是能量，${\displaystyle \theta \,\!}$ 是散射角度。這就是著名的盧瑟福公式^[5]。

假設阿爾法粒子正面碰撞於原子核。阿爾法粒子所有的動能（${\displaystyle mv_{0}^{2}/2\,\!}$），在碰撞點，都被轉換為位能。在那一剎那，阿爾法粒子暫時是停止的。從阿爾法粒子到原子核中心的距離 ${\displaystyle b\,\!}$ 是原子核最大尺寸。應用庫侖定律，

${\displaystyle {\frac {1}{2}}mv_{0}^{2}={\frac {qQ}{4\pi \epsilon _{0}b}}\,\!}$ ；

其中，${\displaystyle m\,\!}$ 是質量，${\displaystyle v_{0}\,\!}$ 是初始速度。

重新編排，

${\displaystyle b={\frac {2qQ}{4\pi \epsilon _{0}mv_{0}^{2}}}\,\!}$ 。

阿爾法粒子的質量是 ${\displaystyle m=6.7\times 10^{-27}\ kg\,\!}$ ，電荷量是 ${\displaystyle q=2\times (1.6\times 10^{-19})\ C\,\!}$ ，初始速度是 ${\displaystyle v_{0}=2\times 10^{7}\ m/s\,\!}$ ，金的電荷量是 ${\displaystyle Q=79\times (1.6\times 10^{-19})\ C\,\!}$ 。將這些數值代入方程式，可以得到撞擊參數 ${\displaystyle b=2.7\times 10^{-14}\ m\,\!}$ （真實半徑是 ${\displaystyle 7.3\times 10^{-15}\ m\,\!}$ ）。這些實驗無法得到真實半徑，因為阿爾法粒子沒有足夠的能量撞入 ${\displaystyle 27\ fm\,\!}$ 半徑內。拉塞福知道這問題。他也知道，假若阿爾法粒子眞能撞至 ${\displaystyle 7.3\ fm\,\!}$ 半徑，直接地擊中金原子核，那麼，在高撞擊角度（最小撞擊參數 ${\displaystyle b\,\!}$ ），由於位勢不再是庫侖位勢，實驗得到的散射曲線的樣子會從雙曲線改變為別種曲線。拉塞福沒有觀察到別種曲線，顯示出金原子核並沒有被擊中。所以，拉塞福只能確定金原子核的半徑小於 ${\displaystyle 27\ fm\,\!}$ 。

1919 年，在拉塞福實驗室進行的另一個非常類似的實驗，物理學家發射阿爾法粒子於氫原子核，觀察到散射曲線顯著地偏離雙曲線，意示位勢不再是庫侖位勢。從實驗數據，物理學家得到撞擊參數或最近離距（closest approach）大約為 ${\displaystyle 3.5\ fm\,\!}$ 。更進一步的研究，在拉塞福實驗室，發射阿爾法粒子於氮原子核和氧原子核，得到的結果，使得詹姆斯·查德威克和工作同仁確信，原子核內的作用力不同於庫侖斥力^[6]。

現今，應用這些年累積的散射原理與技術，拉塞福背散射譜學能夠偵側半導體內的重金屬雜質。實際上，這技術也是第一個在月球使用的實地分析技術。在勘察者任務（surveyor mission）降落於月球表面後，拉塞福背散射譜學實驗被用來收集地質資料。

• 湯姆森散射
• 散射理論