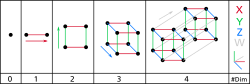µŁŻĶĮ┤ÕĮóÕ£©ÕćĀõĮĢÕŁ”õĖŁ’╝īµŁŻĶĮ┤ÕĮó’╝īµł¢ń¦░õ║żÕÅēÕĮó[1]ŃĆüµŁŻõ║żÕĮó[2]ŃĆüĶČģµŁŻÕģ½ķØóõĮōŃĆüõĮÖµ¢╣ÕĮó’╝īµś»õĖĆõĖ¬µŁŻńÜäŃĆüÕćĖńÜäŃĆüÕŁśÕ£©õ║Äõ╗╗µäÅń╗┤Õ║”ńÜäÕżÜĶā×ÕĮóŃĆ鵣ŻĶĮ┤ÕĮóńÜäķĪČńé╣ÕØɵĀćķāĮµś»(┬▒1, 0, 0, ŌĆ”, 0)ńÜäÕģ©µÄÆÕłŚ’╝īµŁŻĶĮ┤ÕĮ󵜻Ķ┐Öõ║øķĪČńé╣ńÜäÕćĖÕīģŃĆéÕ«āńÜä(n-1)ń╗┤ĶĪ©ķØ󵜻(n-1)ń╗┤ńÜ䵣ŻÕŹĢń║»ÕĮó’╝īĶĆīµŁŻĶĮ┤ÕĮóńÜäķĪČńé╣ÕøŠµś»ÕēŹõĖĆń╗┤ńÜäÕÅ”õĖƵŁŻĶĮ┤ÕĮóŃĆé nń╗┤µŁŻĶĮ┤ÕĮóõ╣¤ÕÅ»õ╗źńö©Õ£©RnõĖŁŌäō1-ĶĄŗĶīāõĖŗńÜäÕŹĢõĮŹńÉā’╝łµł¢ĶĆģ’╝īÕ»╣õ║ĵ¤Éõ║øÕŁ”ĶĆģ’╝īÕŹĢõĮŹńÉāķØó’╝ēµØźÕ«Üõ╣ē’╝ø Õ£©õĖĆń╗┤’╝īµŁŻĶĮ┤ÕĮóÕ░▒µś»ń║┐µ«Ą [ŌłÆ1, +1]’╝īÕ£©õ║īń╗┤Õ«āµś»µŁŻµ¢╣ÕĮó’╝łµł¢ÕŽÕüܵŁŻĶÅ▒ÕĮó’╝ē’╝īµ£ēķĪČńé╣{(┬▒1, 0), (0, ┬▒1)ŃĆéÕ£©õĖēń╗┤Õ«āµś»µŁŻÕģ½ķØóõĮōŌĆöõ║öõĖ¬µŁŻÕżÜķØóõĮō’╝īÕŹ│µ¤ÅµŗēÕøŠń½ŗõĮōõ╣ŗõĖĆŃĆéµø┤ķ½śń╗┤ńÜ䵣ŻĶĮ┤ÕĮóµĆ╗ń╗ōÕ”éõĖŗ’╝Ü
µŁŻĶĮ┤ÕĮ󵜻ĶČģµ¢╣ÕĮóńÜäÕ»╣ÕüČÕżÜĶā×ÕĮóŃĆénń╗┤µŁŻĶĮ┤ÕĮóńÜäõĖĆķśČķ¬©µ×ȵś»Tur├ĪnÕøŠT(2n,n)ŃĆé Õøøń╗┤Õøøń╗┤µŁŻĶĮ┤ÕĮóõ╣¤Ķó½ÕŽÕüܵŁŻÕŹüÕģŁĶā×õĮōŃĆéÕ«āµś»6õĖ¬Õøøń╗┤ÕćĖµŁŻÕżÜĶā×õĮōõ╣ŗõĖĆŃĆéĶ┐Öõ║øÕżÜĶā×õĮōµ£ĆÕģłĶó½ńæ×ÕŻ½µĢ░ÕŁ”Õ«ČĶĘ»ÕŠĘń╗┤ÕĖī┬ʵ¢ĮĶÄ▒Õż½Õł®Õ£©19õĖ¢ń║¬õĖŁµ£¤µÅÅĶ┐░Ķ┐ćŃĆé µø┤ķ½śń╗┤µŁŻĶĮ┤ÕĮóÕ«ČµŚÅµś»õĖēõĖ¬Õ╗Čõ╝ĖĶć│µŁŻµŚĀń®Ęń╗┤ńÜ䵣ŻÕżÜĶā×ÕĮóÕ«ČµŚÅõ╣ŗõĖĆ’╝īĶĆāÕģŗµ¢»ńē╣Õ░åÕģȵĀćĶ«░õĖ║╬▓n’╝īÕÅ”Õż¢õĖżõĖ¬µś»ĶČģµ¢╣ÕĮóÕ«ČµŚÅ’╝īĶ«░õĖ║╬│n’╝īõ╗źÕÅŖÕŹĢń║»ÕĮóÕ«ČµŚÅ’╝īĶ«░õĖ║╬▒nń¼¼ÕøøõĖ¬ķØ×ÕćĖÕżÜĶā×ÕĮóńÜäÕ«ČµŚÅ’╝īĶČģµ¢╣ÕĮóÕ»åķō║Õ«ČµŚÅ’╝īõ╗¢Õ░åÕģȵĀćĶ«░õĖ║╬┤nŃĆé nń╗┤µŁŻĶĮ┤ÕĮóµ£ē2nõĖ¬ķĪČńé╣’╝īÕÅŖ2nõĖ¬Õģ©ķāĮµś»(nŌłÆ1)-ÕŹĢń║»õĮōńÜäń╗┤ķØó’╝łnŌłÆ1 ń╗┤ń╗䵳ÉÕģāń┤Ā’╝ēŃĆéÕ«āńÜäķĪČńé╣ÕøŠ ķāĮµś»n ŌłÆ 1ń╗┤ńÜ䵣ŻĶĮ┤ÕĮóŃĆ鵣ŻĶĮ┤ÕĮóńÜäµ¢ĮĶÄ▒Õż½Õł®ń¼”ÕÅʵś»{3,3,ŌĆ”,3,4}ŃĆén-ń╗┤µŁŻĶĮ┤ÕĮóńÜäõ║īķØóĶ¦Æµś»
n-ń╗┤µŁŻĶĮ┤ÕĮóńÜäk-ń╗┤ń╗䵳ÉÕģāń┤Ā’╝łķĪČńé╣ŃĆüµŻ▒ŃĆüķØóŃĆüŌĆ”ŃĆüń╗┤ķØó’╝ēńÜäõĖ¬µĢ░ńö▒õ╗źõĖŗÕģ¼Õ╝Åń╗ÖÕć║’╝łĶ¦üõ║īķĪ╣Õ╝Åń│╗µĢ░’╝ē’╝Ü n-ń╗┤µŁŻĶĮ┤ÕĮóńÜäĶČģõĮōń¦»õĖ║’╝Ü Ķ┐Öķćīµ£ēĶ«ĖÕżÜĶāĮÕż¤õ╗źõ║īń╗┤ÕøŠÕāÅÕ▒Ģńż║µŁŻĶĮ┤ÕĮóńÜ䵣Żõ║żµŖĢÕĮ▒’╝īńÜ«ńē╣ķćīÕżÜĶŠ╣ÕĮóµŖĢÕĮ▒µś»ÕĖĖńö©ńÜäõĖĆń¦ŹµŖĢÕĮ▒’╝īÕ░åÕģČķĪČńé╣’╝īµŖĢÕĮ▒Õł░õĖĆõĖ¬2nĶŠ╣ÕĮóµł¢µø┤õĮÄķśČńÜ䵣ŻÕżÜĶŠ╣ÕĮóõĖŖŃĆéń¼¼õ║īµ¼ĪńÜäµŖĢÕĮ▒ÕåŹµŖĢÕĮ▒õ║ĵø┤õĮÄń╗┤õĖŁńÜä2(n-1)ĶŠ╣ńÜ«ńē╣ķćīÕżÜĶŠ╣ÕĮó’╝īõŠŗÕ”éÕÅīĶ¦Æķöź’╝īµłæõ╗¼ÕÅ»Õ░åÕģȵ▓┐õĖ╗ĶĮ┤µŖĢÕĮ▒’╝īõĖżõĖ¬ķĪČńé╣Ķó½µŖĢÕĮ▒Õł░õ║åµŖĢÕĮ▒ńÜäõĖŁÕ┐āŃĆé
ńŁēĶĮ┤µŁŻĶĮ┤ÕĮóńÜäķĪČńé╣Õ£©µø╝ÕōłķĪ┐ĶĘØń”╗õĖŗ’╝īõ╗╗µäÅõĖżńé╣õ╣ŗķŚ┤ńÜäĶĘØń”╗ķāĮµś»ńøĖńŁēńÜä’╝łL1ĶĄŗĶ¦ä’╝ēŃĆéÕ║ōµ¢»ń║│ńī£µā│ÕŹ│µś»Ķ»┤Ķ┐ÖõĖ¬ńö▒2d õĖ¬ńé╣ń╗䵳ÉńÜäķøåÕÉłµś»Õ£©Ķ┐ÖĶĘØń”╗õĖŗµ£ĆÕż¦ńÜäńŁēĶĘØķøåŃĆé[3] ÕÅ”Ķ¦ü
µ│©ķćŖ
ÕÅéĶĆā
Õż¢ķā©ķōŠµÄźń╗┤Õ¤║Õģ▒õ║½ĶĄäµ║ÉõĖŖńÜäńøĖÕģ│ÕżÜÕ¬ÆõĮōĶĄäµ║É’╝ܵŁŻĶĮ┤ÕĮó
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia