ķ╗ÅÕ║”
ķ╗ÅÕ║”[1]’╝łĶŗ▒Ķ¬×’╝Üviscosity’╝ēÕŹ│ŌĆ£µĄüõĮōķ╗Åń©ĀńÜäń©ŗÕ║”ŌĆØ’╝īµś»Õ║”ķćŵĄüõĮōķ╗ŵ╗×µĆ¦Õż¦Õ░ÅńÜäńē®ńÉåķćÅŃĆéÕĮōµČ▓õĮōŃĆüµŗ¤µČ▓õĮōµł¢µŗ¤Õø║õĮōńē®Ķ┤©ÕÅŚÕł░Õż¢ķā©Õē¬ÕłćÕŖøõĮ£ńö©µŚČ’╝īÕÅæńö¤ÕĮóÕÅśõĖĵĄüÕŖ©’╝īÕłåÕŁÉķŚ┤õ╝Üõ║¦ńö¤Õåģµæ®µō”µł¢µĄüÕŖ©Õåģķś╗ÕŖø’╝īĶĪ©ÕŠüµŁżńøĖÕ║öńÜäµŖŚÕĮóÕÅśŃĆüµŖŚµĄüÕŖ©ńē╣µĆ¦ńÜäńē®ńÉåķćÅ’╝īÕ░▒µś»ķ╗ÅÕ║”ŃĆéķ╗ÅÕ║”ńÜäń¦æÕŁ”Õ«Üõ╣ēµś»ÕŖøõ╣śõ╗źµŚČķŚ┤ķÖżõ╗źķØóń¦»ŃĆéÕøĀµŁż’╝īÕģČÕøĮķÖģÕŹĢõĮŹÕłČõĖ║ńēøķĪ┐ń¦Æµ»ÅÕ╣│µ¢╣ń▒│’╝īµł¢ÕĖĢµ¢»ÕŹĪń¦ÆŃĆé[2] ķ╗ÅÕ║”õ╣¤ń¦░ÕŖ©ÕŖøķ╗ÅÕ║”ŃĆüķ╗Å’╝łµ╗×’╝ēµĆ¦ń│╗µĢ░ŃĆüÕåģµæ®µō”ń│╗µĢ░ŃĆéõĖŹÕÉīńē®Ķ┤©ńÜäķ╗ÅÕ║”õĖŹÕÉī’╝īõŠŗÕ”éÕ£©Õ«żµĖ®’╝ł25Ōäā’╝ēÕÅŖÕĖĖÕÄŗ’╝ł1ÕĘ┤’╝ēõĖŗ’╝īń®║µ░öńÜäķ╗ÅÕ║”õĖ║18.5 ╬╝Pa┬Ęs’╝īÕż¦ń┤䵜»Õ£©ńøĖÕÉīµĖ®Õ║”õĖŗńÜäµ░┤ķ╗ÅÕ║”ńÜä1/50ŃĆéÕ£©ÕĖĖµĖ®’╝ł20Ōäā’╝ēÕĖĖÕÄŗõĖŗ’╝īµ▒Įµ▓╣ńÜäķ╗ÅÕ║”õĖ║0.65 mPa┬Ęs’╝īµ░┤õĖ║1 mPa┬Ęs’╝īĶĪƵČ▓’╝ł37Ōäā’╝ēõĖ║4’Į×15 mPa┬Ęs’╝īµ®äµ”äµ▓╣õĖ║102 mPa┬Ęs’╝īĶō¢ķ║╗µ▓╣õĖ║103 mPa┬Ęs’╝īĶ£éĶ££õĖ║104 mPa┬Ęs’╝īń䔵▓╣õĖ║106 mPa┬Ęs’╝īµ▓źķØÆõĖ║108 mPa┬ĘsńŁēńŁēŃĆé[3]  ķ╗ŵ╗»ÕŖøµś»µĄüķ½öÕÅŚÕł░Õē¬µćēÕŖøĶ«ŖÕĮóµł¢µŗēõ╝ĖµćēÕŖøµÖéµēĆńöóńö¤ńÜäķś╗ÕŖøŃĆéÕ£©µŚźÕĖĖńö¤µ┤╗µ¢╣ķØó’╝īķ╗ŵ╗»Õāŵś»ŃĆīķ╗Åń©ĀÕ║”ŃĆŹµł¢ŃĆīµĄüķ½öÕģ¦ńÜäµæ®µō”ÕŖøŃĆŹŃĆéÕøĀµŁż’╝īµ░┤µś»ŃĆīń©ĆĶ¢äŃĆŹńÜä’╝īÕģʵ£ēĶ╝āõĮÄńÜäķ╗ŵ╗»ÕŖø’╝īĶĆīĶ£éĶ££µś»ŃĆīµ┐āń©ĀŃĆŹńÜä’╝īÕģʵ£ēĶ╝āķ½śńÜäķ╗ŵ╗»ÕŖøŃĆéń░ĪÕ¢«Õ£░Ķ¬¬’╝īķ╗ŵ╗»ÕŖøĶČŖõĮÄ’╝łķ╗ŵ╗»õ┐éµĢĖõĮÄ’╝ēńÜ䵥üķ½ö’╝īµĄüÕŗĢµĆ¦ĶČŖõĮ│ŃĆé ķ╗ŵ╗»ÕŖøµś»ķ╗ÅµĆ¦µČ▓ķ½öÕģ¦ķā©ńÜäõĖĆń©«µĄüÕŗĢķś╗ÕŖø’╝īõĖ”ÕÅ»ĶāĮĶó½Ķ¬Źńé║µś»µĄüķ½öĶć¬Ķ║½ńÜäµæ®µō”ŃĆéķ╗ŵ╗»ÕŖøõĖ╗Ķ”üõŠåĶć¬ÕłåÕŁÉķ¢ōńøĖõ║ÆńÜäÕÉĖÕ╝ĢÕŖøŃĆéõŠŗÕ”é’╝īķ½śķ╗ÅÕ║”ķģĖµĆ¦ńåöÕ▓®ńöóńö¤ńÜäńü½Õ▒▒ķĆÜÕĖĖńé║ķ½śĶĆīķÖĪÕ│ŁńÜäķīÉńŗĆńü½Õ▒▒’╝īÕøĀńé║ÕģČńåöÕ▓®µ┐āń©Ā’╝īÕ£©ÕģČÕåĘÕŹ╗õ╣ŗÕēŹńäĪµ│ĢµĄüĶć│ķüĀĶĘØķøóÕøĀĶĆīõĖŹµ¢ĘÕÉæõĖŖń┤»ÕŖĀ’╝øĶĆīķ╗ŵ╗»ÕŖøõĮÄńÜäķÄéķÉĄĶ│¬ńåöÕ▓®Õ░ćÕ╗║ń½ŗõĖĆÕĆŗÕż¦Ķ”ŵ©ĪŃĆüµĘ║ÕéŠńÜäńøŠńŗĆńü½Õ▒▒ŃĆéµēƵ£ēń£¤µŁŻńÜ䵥üķ½ö’╝łķÖżĶČģµĄüķ½ö’╝ēµ£ēõĖĆÕ«ÜńÜäµŖŚÕŻōÕŖø’╝īÕøĀµŁżµ£ēķ╗ÅµĆ¦ŃĆéµ▓Ƶ£ēķś╗ÕŖøÕ░ŹµŖŚÕē¬ÕłćµćēÕŖøńÜ䵥üķ½öĶó½ń©▒ńé║ńÉåµā│µĄüķ½öµł¢ńäĪķ╗ŵĄüķ½öŃĆé ķøČķ╗ÅÕ║”’╝łÕ»╣Õē¬ÕłćÕ║öÕŖøµ▓Īµ£ēµŖĄµŖŚÕŖø’╝ēõ╗ģÕ£©ĶČģµĄüõĮōńÜäµ×üõĮĵĖ®Õ║”õĖŗĶ¦éÕ»¤Õł░’╝øÕÉ”ÕłÖ’╝īńāŁÕŖøÕŁ”ń¼¼õ║īÕ«ÜÕŠŗĶ”üµ▒éµēƵ£ēµĄüõĮōķāĮÕģʵ£ēµŁŻķ╗ÅÕ║”ŃĆéÕģʵ£ēķøČķ╗ÅÕ║”’╝łķØ×ķ╗ÅµĆ¦’╝ēńÜ䵥üõĮōń¦░õĖ║ńÉåµā│µĄüõĮōµł¢µŚĀķ╗ÅµĆ¦µĄüõĮōŃĆé ķ╗ÅÕ║”Õ«ÜńŠ®ńé║µĄüķ½öµē┐ÕÅŚÕē¬µćēÕŖøµÖé’╝īÕē¬µćēÕŖøĶłćµĄüõĮōÕŹĢõĮŹķƤÕ║”ÕĘ«ńÜäµ»öÕĆ╝’╝īµĢ░ÕŁ”ĶĪ©Ķ┐░õĖ║’╝Ü Õ╝ÅõĖŁ’╝ÜõĖ║Õē¬Õ║öÕŖø’╝īõĖ║ķƤÕ║”Õ£║Õ£©µ¢╣ÕÉæńÜäÕłåķćÅ’╝īõĖ║õĖÄÕ×éńø┤ńÜäµ¢╣ÕÉæÕØɵĀćŃĆé Ķ»Źµ║ÉŌĆ£ķ╗ÅµĆ¦’╝łviscosity’╝ēŌĆص║ÉĶć¬ÕÅżµ│ĢĶ»Łviscositeµł¢ńø┤µÄźµ║ÉĶć¬õĖŁõĖ¢ń║¬µŗēõĖüĶ»Ł vicositatem’╝łõĖ╗µĀ╝ vicositas’╝ē’╝īµ║ÉĶ欵Öܵ£¤µŗēõĖüĶ»Łviscosus’╝īńø┤µÄźµ║Éõ║ĵŗēõĖüĶ»Łviscum’╝īµī浦▓Õ»äńö¤’╝īńö©µ¦▓Õ»äńö¤ŃĆüµ¦▓Õ»äńö¤ÕłČµłÉńÜäķĖ¤ń▓¬ńŁēķ╗ÅµĆ¦ńÜäõĖ£Ķź┐’╝īõ╣¤µīćõ╗ĵ¦▓Õ»äńö¤µĄåµ×£õĖŁµÅÉÕÅ¢ńÜäķ╗Åń©ĀĶāȵ░┤’╝ī[5]ÕÅ»ĶāĮµ║Éõ║ÄĶ»ŹµĀ╣*weis-’╝īńö©õ║ĵÅÅĶ┐░µüČĶ棵ł¢µ£ēÕ╝éÕæ│ńÜäµČ▓õĮōŃĆé[6] õ║¦ńö¤µĄüõĮōńÜäķ╗ÅÕ║”µś»ńö▒õ║ÄńøĖķé╗Õ▒éķŚ┤õ╗źõĖŹÕÉīńÜäķƤÕ║”Ķ┐ÉÕŖ©µŚČõ║¦ńö¤ńÜäµæ®µō”ķĆĀµłÉńÜäŃĆéÕĮōķ╗ÅµĆ¦µĄüõĮōÕÅŚĶ┐½ķĆÜĶ┐ćń«ĪķüōµŚČ’╝īÕ«āÕ£©ń«ĪķüōõĖŁÕ┐āń║┐ķÖäĶ┐æńÜ䵥üÕŖ©ķƤÕ║”µ»öÕ£©ń«ĪķüōÕŻüķÖäĶ┐æńÜ䵥üÕŖ©ķƤÕ║”µø┤Õ┐½ŃĆé[7]ÕøĀõĖ║ķ£ĆĶ”üÕŖøµØźÕģŗµ£ŹńøĖÕ»╣Ķ┐ÉÕŖ©ńÜ䵥üõĮōÕ▒éõ╣ŗķŚ┤ńÜäµæ®µō”’╝īµēĆõ╗źķ£ĆĶ”üõĖĆÕ«ÜńÜäÕ║öÕŖø’╝łõŠŗÕ”éń«ĪķüōõĖżń½»õ╣ŗķŚ┤ńÜäÕÄŗÕŖøÕĘ«’╝ēµØźń╗┤µīüµĄüÕŖ©ŃĆéÕ»╣õ║ĵĄüķƤµüÆÕ«ÜńÜäń«Īķüō’╝īĶĪźÕü┐ÕŖøńÜäÕ╝║Õ║”õĖĵĄüõĮōńÜäķ╗ÅÕ║”µłÉµŁŻµ»öŃĆéń«ĪõĖŁÕ┐āÕżäķś╗ÕŖøµ£ĆÕ░Å’╝īµČ▓Õ▒鵥üÕŖ©ķƤÕ║”µ£ĆÕż¦’╝øń«ĪÕŻüķÖäĶ┐æµČ▓Õ▒éÕÉīµŚČÕÅŚÕł░µČ▓õĮōķ╗ÅµĆ¦ķś╗ÕŖøÕÆīń«ĪÕŻüµæ®µō”ÕŖøõĮ£ńö©’╝īķƤÕ║”µ£ĆÕ░Å’╝īÕ£©ń«ĪÕŻüõĖŖµČ▓Õ▒éńÜäń¦╗ÕŖ©ķƤÕ║”õĖ║ķøČ’╝łÕüćÕ«ÜÕ£©õĖŹõ║¦ńö¤µ╗æń¦╗µŚČ’╝ēŃĆé ķ╗ÅÕ║”ķćÅÕī¢õ║åńøĖÕ»╣Ķ┐ÉÕŖ©ńÜäńøĖķé╗µĄüõĮōÕ▒éõ╣ŗķŚ┤ńÜäÕåģķā©µæ®µō”ÕŖøŃĆé[2]µ£ĆµÖ«ķĆÜńÜäµČ▓õĮōķ╗ÅÕ║”Õż¦Ķć┤Õ£©1~1000 mPa┬Ęs’╝īµ░öõĮōńÜäķ╗ÅÕ║”Õż¦Ķć┤Õ£©1~10 ╬╝Pa┬ĘsŃĆéõĖĆõ║øÕāÅķ╗äµ▓╣µł¢õ║║ķĆĀķ╗äµ▓╣ńÜäĶäéĶé¬ÕŠłķ╗Å’╝īµø┤ÕāÅĶĮ»ńÜäÕø║õĮō’╝īĶĆīõĖŹµś»µĄüÕŖ©µČ▓õĮōŃĆéķ╗ÅÕ║”Ķ╝āķ½śńÜäńē®Ķ│¬’╝īµ»öĶ╝āõĖŹÕ«╣µśōµĄüÕŗĢ’╝øĶĆīķ╗ÅÕ║”Ķ╝āõĮÄńÜäńē®Ķ│¬’╝īµ»öĶ╝āÕ«╣µśōµĄüÕŗĢŃĆéõŠŗÕ”éµ▓╣ńÜäķ╗ÅÕ║”Ķ╝āķ½ś’╝īÕøĀµŁżõĖŹÕ«╣µśōµĄüÕŗĢ’╝øĶĆīµ░┤ķ╗ÅÕ║”Ķ╝āõĮÄ’╝īõĖŹõĮåÕ«╣µśōµĄüÕŗĢ’╝īÕĆƵ░┤µÖéķéäµ£āÕć║ńÅŠµ░┤ĶŖ▒’╝īÕĆƵ▓╣µÖéÕ░▒õĖŹµ£āÕć║ńÅŠķĪ×õ╝╝ńÜäńÅŠĶ▒ĪŃĆé Õłåń▒╗Õ«×ķÖģõĖŖ’╝īµ£ēõĖżõĖ¬ķćÅĶó½ń¦░õĖ║ķ╗ÅÕ║”ŃĆéõĖĆń¦ŹĶó½ń¦░õĖ║ÕŖ©µĆüķ╗ÅÕ║”ŃĆüń╗ØÕ»╣ķ╗ÅÕ║”µł¢ń«ĆÕŹĢķ╗ÅÕ║”’╝łµØźÕī║Õł½ÕģČõ╗¢ńÜäķćÅ’╝ē’╝īõĮåķĆÜÕĖĖõ╣¤ń¦░õĖ║ķ╗ÅÕ║”ŃĆéÕÅ”Õż¢õĖĆń¦ŹķćÅń¦░õĖ║Ķ┐ÉÕŖ©ķ╗ÅÕ║”’╝łńö©ń¼”ÕÅĘ╬ĮĶĪ©ńż║’╝ē’╝īÕ«āµś»µĄüõĮōńÜäķ╗ÅÕ║”õĖÄÕ»åÕ║”ńÜäµ»öÕĆ╝ŃĆé ÕŖĀÕĘźĶ┐ćń©ŗõĖŁ’╝īĶüÜÕÉłńē®ńÜ䵥üÕÅśµĆ¦Ķ┤©õĖ╗Ķ”üĶĪ©ńÄ░õĖ║ķ╗ÅÕ║”ńÜäÕÅśÕī¢’╝īµĀ╣µŹ«µĄüÕŖ©Ķ┐ćń©ŗõĖŁĶüÜÕÉłńē®ķ╗ÅÕ║”õĖÄÕ║öÕŖøµł¢Õ║öÕÅśķƤńÄćńÜäÕģ│ń│╗’╝īÕ░åĶüÜÕÉłńē®ńÜ䵥üÕŖ©ĶĪīõĖ║ÕłåõĖ║’╝ÜńēøķĪ┐µĄüõĮōŌĆöŌĆöķ╗ÅÕ║”╬╝õĖ║ÕĖĖµĢ░’╝øķØ×ńēøķĪ┐µĄüõĮōŌĆöŌĆöĶĪ©Ķ¦éķ╗ÅÕ║”╬╝õĖŹõĖ║ÕĖĖµĢ░ŃĆé õĖĆĶł¼µØźĶ»┤’╝īķ╗ÅÕ║”ÕÅ¢Õå│õ║ĵĄüõĮōńÜäńŖȵĆü’╝īõŠŗÕ”éÕģȵĖ®Õ║”ŃĆüÕÄŗÕŖøÕÆīÕÅśÕĮóńÄćŃĆéńäČĶĆī’╝īÕ£©µ¤Éõ║øµāģÕåĄõĖŗ’╝īÕ»╣ÕģČõĖŁõĖĆõ║øÕ▒׵ƦńÜäõŠØĶĄ¢µĆ¦ÕÅ»õ╗źÕ┐ĮńĢźõĖŹĶ«ĪŃĆéõŠŗÕ”éńēøķĪ┐µĄüõĮōńÜäķ╗ÅÕ║”Õ░▒õĖŹõ╝ÜķÜÅÕÅśÕĮóńÄćÕÅæńö¤µśŠńØĆÕÅśÕī¢ŃĆéÕ»╣õ║ÄķØ×ńēøķĪ┐µĄüõĮōńÜäķ╗ÅÕ║”’╝īÕŁśÕ£©õĖĵŚČķŚ┤µŚĀÕģ│ńÜäÕüćÕĪæµĆ¦µĄüÕŖ©ŃĆüÕĪæµĆ¦µĄüÕŖ©ÕÆīĶå©ĶāƵƦµĄüÕŖ©’╝īõ╗źÕÅŖõĖĵŚČķŚ┤ńøĖÕģ│ńÜäĶ¦”ÕÅśµĆ¦µĄüÕŖ©ÕÆīµĄüÕÅśµĆ¦µĄüÕŖ©ŃĆé Õ«Üõ╣ēÕē¬Õłćķ╗ÅÕ║” µØɵ¢Öń¦æÕŁ”õĖÄÕĘźń©ŗõĖŁ’╝īõ║║õ╗¼ķĆÜÕĖĖÕ»╣õ║åĶ¦ŻµØɵ¢ÖÕÅśÕĮóµēƵČēÕÅŖńÜäÕŖøµł¢Õ║öÕŖøµä¤Õģ┤ĶČŻŃĆéÕ”éµ×£µØɵ¢Öµś»õĖĆõĖ¬ń«ĆÕŹĢńÜäÕ╝╣ń░¦’╝īķéŻÕ░åńö©ĶĪ©µśÄÕ╝╣ń░¦µēĆÕÅŚńÜäÕŖøõĖÄÕüÅń”╗Õ╣│ĶĪĪõĮŹńĮ«ńÜäĶĘØń”╗µłÉµŁŻµ»öńÜäĶāĪÕģŗÕ«ÜÕŠŗĶ«Īń«ŚŃĆéÕÅ»ÕĮÆÕøĀõ║ĵØɵ¢Öõ╗ĵ¤ÉõĖĆķØÖµŁóńŖȵĆüÕÅśÕĮóńÜäÕ║öÕŖøń¦░õĖ║Õ╝╣µĆ¦Õ║öÕŖøŃĆéÕ£©ÕģČõ╗¢µØɵ¢ÖõĖŁ’╝īÕŁśÕ£©ńÜäÕ║öÕŖøÕÅ»ÕĮÆÕøĀõ║ÄķÜŵŚČķŚ┤ÕÅśÕī¢ńÜäÕÅśÕĮóńÄć’╝īń¦░õĖ║ķ╗ÅµĆ¦Õ║öÕŖøŃĆéõŠŗÕ”é’╝īÕ£©µ░┤ńŁēµĄüõĮōõĖŁ’╝īńö▒Õē¬ÕłćµĄüõĮōõ║¦ńö¤ńÜäÕ║öÕŖøõĖŹÕÅ¢Õå│õ║ĵĄüõĮōĶó½Õē¬ÕłćńÜäĶĘØń”╗ĶĆīÕÅ¢Õå│õ║ÄÕē¬ÕłćńÜäķƤÕ║”ŃĆé ķ╗ÅÕ║”µś»õĖĆń¦ŹµØɵ¢Öńē╣µĆ¦’╝īÕ«āÕ░åµØɵ¢ÖõĖŁńÜäķ╗ÅµĆ¦Õ║öÕŖøõĖÄÕÅśÕĮóńÜäÕÅśÕī¢ńÄć’╝łÕ║öÕÅśńÄć’╝ēĶüöń│╗ĶĄĘµØź’╝īķĆéńö©õ║ÄõĖĆĶł¼ńÜ䵥üÕŖ©’╝īÕ£©ń«ĆÕŹĢńÜäÕē¬ÕłćµĄü’╝łõŠŗÕ”éµŗ¢µø│µĄüÕŖ©’╝ēõĖŁÕŠłÕ«╣µśōÕĮóĶ▒ĪÕī¢ÕÆīÕ«Üõ╣ēŃĆé ĶĆīµĄüõĮōÕÆīń¦╗ÕŖ©ĶŠ╣ńĢīõ╣ŗķŚ┤ńÜäµæ®µō”Õ»╝Ķć┤õ║åµĄüõĮōÕē¬Õłć’╝īµÅÅĶ┐░Ķ┐Öń¦ŹĶĪīõĖ║Õ╝║Õ║”ńÜ䵜»µĄüõĮōńÜäķ╗ÅÕ║”ŃĆéÕ£©õĖĆĶł¼ńÜäÕ╣│ĶĪīµĄüÕŖ©õĖŁ’╝łÕ”éÕÅ»ĶāĮÕÅæńö¤Õ£©õĖĆõĖ¬ńø┤ń«ĪõĖŁ’╝ē’╝īÕē¬ÕłćÕ║öÕŖøµŁŻµ»öõ║ÄķƤÕ║”µó»Õ║”ŃĆéńøĖõ║ÆÕ╣│ĶĪīńÜäńøĖķé╗Õ▒éõ╣ŗķŚ┤ńÜäń¦╗ÕŖ©ķƤÕ║”õĖŹÕÉī’╝īõ║¦ńö¤Õē¬ÕłćŃĆéĶĆīµĄüõĮōńÜäÕē¬Õłćķ╗ÅÕ║”µś»µÅÅĶ┐░Õ»╣Õē¬ÕłćµĄüÕŖ©ńÜäµŖĄµŖŚĶāĮÕŖøŃĆéńÉåµā│µāģÕåĄķ╗ÅÕ║”ÕŻիÜõ╣ēõĖ║µŗ¢µø│µĄüÕŖ©ŌĆöŌĆöĶó½Õø░Õ£©µ░┤Õ╣│µØ┐’╝łõĖĆõŠ¦Õø║Õ«Ü’╝īõĖĆõŠ¦õ╗źµüÆÕ«ÜķƤÕ║”µ░┤Õ╣│Ķ┐ÉÕŖ©’╝ēķŚ┤ńÜäõĖĆÕ▒鵥üõĮō’╝łķĆÜÕĖĖĶ«żõĖ║µØ┐ÕØŚķØ×ÕĖĖÕż¦’╝īõĖŹķ£ĆĶ”üĶĆāĶÖæĶŠ╣ń╝śķÖäĶ┐æńÜäµāģÕåĄ’╝ēŃĆéÕ£©µŗ¢µø│µĄüÕŖ©õĖŁ’╝īµĄüõĮōĶó½Õø░Õ£©õĖżõĖ¬µŚĀķÖÉÕż¦ńÜäÕ╣│µØ┐õ╣ŗķŚ┤’╝īõĖĆõĖ¬Õ╣│µØ┐Õø║Õ«Ü’╝īÕÅ”õĖĆõĖ¬Õ╣│µØ┐õ╗źµüÆÕ«ÜķƤÕ║”Õ╣│ĶĪīĶ┐ÉÕŖ©’╝łÕÅ│ÕøŠ’╝ēŃĆéÕ”éµ×£ķĪȵØ┐ńÜäķƤÕ║”ĶČ│Õż¤õĮÄ’╝łõ╗źķü┐ÕģŹµ╣ŹµĄü’╝ē’╝īķéŻõ╣łÕ£©ń©│Õ«ÜńŖȵĆüõĖŗ’╝īµĄüõĮōń▓ÆÕŁÉõ╝ÜÕ╣│ĶĪīõ║ÄķĪȵØ┐ń¦╗ÕŖ©’╝īÕģČķƤÕ║”õ╝ÜÕÅśÕī¢Õ£©Õ║Ģķā©ķĪČķā©ŃĆé[8]µ»ÅõĖĆÕ▒鵥üõĮōńÜäĶ┐ÉÕŖ©ķƤÕ║”ķāĮµ»öÕģČõĖŗµ¢╣ńÜäõĖĆÕ▒éÕ┐½’╝īÕ«āõ╗¼õ╣ŗķŚ┤ńÜäµæ®µō”ÕŖøõ╝Üõ║¦ńö¤ķś╗ńóŹÕ«āõ╗¼ńøĖÕ»╣Ķ┐ÉÕŖ©ńÜäÕŖøŃĆéÕģĘõĮōµØźĶ»┤’╝īµĄüõĮōÕ»╣ķĪȵØ┐µ¢ĮÕŖĀõĖĆõĖ¬õĖÄÕģČĶ┐ÉÕŖ©µ¢╣ÕÉæńøĖÕÅŹńÜäÕŖø’╝īÕ»╣Õ║ĢµØ┐µ¢ĮÕŖĀõĖĆõĖ¬ńøĖńŁēõĮåµ¢╣ÕÉæńøĖÕÅŹńÜäÕŖøŃĆéÕøĀµŁż’╝īķ£ĆĶ”üÕż¢ÕŖøµØźõ┐صīüķĪȵØ┐õ╗źµüÆÕ«ÜķƤÕ║”ń¦╗ÕŖ©ŃĆé  Õ”éµ×£ķĪȵØ┐ńÜäķƤÕ║”ĶČ│Õż¤Õ░Å’╝īµĄüõĮōń▓ÆÕŁÉÕ░åÕ╣│ĶĪīõ║ÄÕ«āµĄüÕŖ©’╝īÕ╣ČõĖöÕ«āõ╗¼ńÜäķƤÕ║”õ╗ÄÕ║Ģķā©ńÜä0Õł░ķĪČķā©ńÜäÕæłń║┐µĆ¦ÕÅśÕī¢ŃĆ鵥üõĮōńÜäµ»ÅõĖĆÕ▒鵥üÕŖ©ķƤÕ║”Õ┐½õ║ÄÕ«āńÜäõĖŗõĖĆÕ▒é’╝īÕ«āõ╗¼õ╣ŗķŚ┤õ╝Üõ║¦ńö¤õĖĆõĖ¬µŖĄµŖŚÕ«āõ╗¼ńøĖÕ»╣Ķ┐ÉÕŖ©ńÜäµæ®µō”ÕŖøŃĆéńē╣Õł½µś»’╝īµĄüõĮōÕ░åÕ£©ķĪȵØ┐Ķ┐ÉÕŖ©ńÜäÕÅŹµ¢╣ÕÉæµ¢ĮÕŖĀõĖĆõĖ¬ÕŖø’╝īÕ£©Õ║ĢµØ┐õ╣¤õ╝Üõ║¦ńö¤õĖĆõĖ¬ńŁēÕż¦ÕÅŹÕÉæńÜäÕŖøŃĆéÕøĀµŁżķ£ĆĶ”üõĖĆõĖ¬Õż¢ÕŖøµØźń╗┤µīüķĪȵØ┐õ╗źµüÆÕ«ÜńÜäķƤÕ║”Ķ┐ÉÕŖ©ŃĆéÕŖøńÜäÕż¦Õ░ŵŁŻµ»öõ║ĵ»ÅÕØŚµØ┐ńÜäĶ┐ÉÕŖ©ķƤÕ║”ÕÆīķØóń¦»’╝īĶĆīÕÅŹµ»öõ║ÄõĖżµØ┐õ╣ŗķŚ┤ńÜäĶĘØń”╗’╝īÕŠŚÕł░’╝ÜŃĆĆ Õ£©Ķ┐ÖõĖ¬Õģ¼Õ╝ÅõĖŁ’╝īµ»öõŠŗń│╗µĢ░µś»µĄüõĮōńÜäķ╗ÅÕ║”’╝łńē╣Õł½µś»ÕŖ©µĆüķ╗ÅÕ║”’╝ēÕŖ©µĆüķ╗ÅÕ║”ńÜäķćÅń║▓õĖ║’╝ÜĶ┤©ķćÅ/ĶĘØń”╗/µŚČķŚ┤’╝īÕøĀµŁżÕŻՊŚÕøĮķÖģÕŹĢõĮŹÕÆīµ┤Šńö¤ÕŹĢõĮŹ’╝Ü
ń¦░õĖ║Õē¬ÕłćÕÅśÕĮóµł¢Õē¬ÕłćķƤÕ║”’╝īµś»Õ×éńø┤õ║ĵØ┐ńÜäķƤÕ║”õĖŖµĄüõĮōķƤÕ║”ńÜäÕ»╝µĢ░’╝łÕÅ│ÕøŠ’╝ēŃĆéÕ”éµ×£õĖżĶĆģõĖŹµś»ń║┐µĆ¦ńøĖÕģ│’╝īÕłÖÕÅ»ńö©ÕŠ«Õłåµ¢╣ń©ŗĶĪ©ĶŠŠÕē¬ÕłćÕ║öÕŖø’╝Ü
Ķ┐ÖõĖ¬Õģ¼Õ╝ÅÕüćĶ«ŠµĄüÕŖ©µś»µ▓┐ńØĆÕ╣│ĶĪīń║┐ńÜä’╝īÕ╣ČõĖöÕ×éńø┤õ║ĵĄüÕŖ©µ¢╣ÕÉæńÜäyĶĮ┤µīćÕÉæµ£ĆÕż¦Õē¬ÕłćķƤÕ║”ŃĆéĶ┐ÖõĖ¬µ¢╣ń©ŗÕÅ»õ╗źńö©õ║ÄķƤÕ║”ķØ×ń║┐µĆ¦ÕÅśÕī¢ńÜäµāģÕåĄ’╝īµ»öÕ”éÕ£©µĄüõĮōµĄüń╗Åń«ĪķüōõĖŁµŚČńÜäµāģÕåĄŃĆéÕģČõĖŁ’╝īµś»Õ▒Ćķā©Õē¬ÕłćķƤÕ║”ŃĆéĶ┐ÖõĖ¬ĶĪ©ĶŠŠÕ╝ÅĶó½ń¦░õĖ║ńēøķĪ┐ķ╗ÅµĆ¦Õ«ÜÕŠŗŃĆéÕ£©Õģʵ£ēÕ╣│ķØóÕ»╣ń¦░µĆ¦ńÜäÕē¬ÕłćµĄüõĖŁ’╝īÕģ¼Õ╝ÅÕ«Üõ╣ēõ║å’╝īµś»ķ╗ÅÕ║”õĖĆĶł¼Õ«Üõ╣ēõĖŁńÜäńē╣õŠŗ’╝īÕÅ»ńö©µŚĀÕØɵĀćÕĮóÕ╝ÅĶĪ©ńż║ŃĆé µ£║µó░ÕÆīÕī¢ÕŁ”ÕĘźń©ŗÕĖłŃĆüµĢ░ÕŁ”Õ«Čõ╗źÕÅŖńē®ńÉåÕŁ”Õ«Čõ╗¼ÕĖĖõĮ┐ńö©ÕĖīĶģŖÕŁŚµ»ŹµØźĶĪ©ńż║ÕŖ©µĆüÕÄŗÕŖøķ╗ÅÕ║”’╝ī[9][10][11]ńäČĶĆīÕī¢ÕŁ”Õ«ČŃĆüńē®ńÉåÕŁ”Õ«ČŃĆüIUPACõ╣¤õĮ┐ńö©ÕĖīĶģŖÕŁŚµ»ŹĶĪ©ńż║ŃĆé[12]ķ╗ÅÕ║”µ£ēµŚČõ╣¤ń¦░õĖ║Õē¬Õłćķ╗ÅÕ║”ŃĆéńäČĶĆī’╝īµ£ēõĮ£ĶĆģõĖŹķ╝ōÕŖ▒õĮ┐ńö©Ķ┐ÖõĖ¬µ£»Ķ»Ł’╝īõ╗¢µīćÕć║ķÖżÕē¬ÕłćµĄüÕż¢’╝īĶ┐śÕÅ»Õć║ńÄ░Õ£©ķØ×Õē¬ÕłćµĄüõĖŁŃĆé[13] Ķ┐ÉÕŖ©ķ╗ÅÕ║”µĄüõĮōÕŖ©ÕŖøÕŁ”õĖŁ’╝īµ£ēµŚČńö©Ķ┐ÉÕŖ©ķ╗ÅÕ║”’╝łµ£ēµŚČõ╣¤ń¦░õĖ║ÕŖ©ķćŵē®µĢŻńÄć’╝ēµØźĶĪ©ńż║’╝īĶ┐ÉÕŖ©ķ╗ÅÕ║”Õ«Üõ╣ēõĖ║Õē¬Õłćķ╗ÅÕ║”╬╝ķÖżõ╗źµČ▓õĮōÕ»åÕ║”Žü’╝īķĆÜÕĖĖńö©ÕĖīĶģŖÕŁŚµ»Ź╬ĮĶĪ©ńż║ŃĆé
ķćÅń║▓õĖ║’╝Ü(ķĢ┐Õ║”)2/µŚČķŚ┤’╝īÕŠŚÕł░SIÕŹĢõĮŹÕÅŖµ┤Šńö¤ÕŹĢõĮŹ’╝ī µ»öĶāĮõ╣śõ╗źµŚČķŚ┤µł¢ÕŹĢõĮŹĶ┤©ķćÅńÜäĶāĮķćÅõ╣śõ╗źµŚČķŚ┤’╝Ü
Ķ┐ÉÕŖ©ķ╗ÅÕ║”ÕÅ»ńö©µØźńĀöń®ČķøĘĶ»║µĢ░ŃĆé
õĖĆĶł¼Õ«Üõ╣ēõĖĆĶł¼ĶĆīĶ©Ć’╝īµĄüõĮōõĖŁńÜäķ╗ÅµĆ¦Õ║öÕŖøÕ«Üõ╣ēõĖ║ńö▒õĖŹÕÉīµĄüõĮōń▓ÆÕŁÉńÜäńøĖÕ»╣ķƤÕ║”Õ╝ĢĶĄĘńÜäÕ║öÕŖøŃĆéÕøĀµŁż’╝īķ╗ÅµĆ¦Õ║öÕŖøÕ┐ģķĪ╗ÕÅ¢Õå│õ║ĵĄüķƤńÜäń®║ķŚ┤µó»Õ║”ŃĆéÕ”éµ×£ķƤÕ║”µó»Õ║”ÕŠłÕ░Å’╝īÕłÖķ╗ÅµĆ¦Õ║öÕŖøÕ£©õĖĆķśČĶ┐æõ╝╝õĖŗõ╗ģÕÅ¢Õå│õ║ÄķƤÕ║”ńÜäõĖĆķśČÕ»╝µĢ░’╝īÕ»╣õ║ÄńēøķĪ┐µĄüõĮō’╝īÕłÖõĖ║ń║┐µĆ¦õŠØĶĄ¢Õģ│ń│╗ŃĆéÕ£©ń¼øÕŹĪÕ░öÕØɵĀćń│╗õĖŁ’╝īõĖĆĶł¼Õģ│ń│╗ÕÅ»õ╗źÕåÖµłÉ’╝Ü
ÕģČõĖŁµś»ķƤÕ║”µó»Õ║”Õ╝ĀķćŵśĀÕ░äÕł░ķ╗ÅµĆ¦Õ║öÕŖøÕ╝ĀķćÅńÜäķ╗ÅÕ║”Õ╝ĀķćÅŃĆé[14]ńö▒õ║ÄĶ»źĶĪ©ĶŠŠÕ╝ÅõĖŁńÜäµīćµĢ░ÕÅ»õ╗źÕ£©1~3ķŚ┤ÕÅśÕī¢’╝īÕøĀµŁżµĆ╗Õģ▒µ£ē81õĖ¬ŌĆ£ķ╗ÅÕ║”ń│╗µĢ░ŌĆØŃĆéńäČĶĆī’╝īÕüćĶ«Šķ╗ÅÕ║”ń¦®õĖ║2ńÜäÕ╝Āķćŵś»ÕÉäÕÉæÕÉīµĆ¦ńÜä’╝īÕłÖÕ░åĶ┐Ö81õĖ¬ń│╗µĢ░ń«ĆÕī¢õĖ║õĖēõĖ¬ńŗ¼ń½ŗÕÅéµĢ░’╝ī’╝ī’╝Ü
ÕüćĶ«ŠµĄüõĮōÕ£©Ķ┐øĶĪīń«ĆÕŹĢńÜäÕłÜõĮōµŚŗĶĮ¼µŚČõĖŹõ╝Üõ║¦ńö¤ķ╗ÅµĆ¦ÕŖø’╝īÕøĀµŁż’╝īÕŬÕē®õĖŗõĖżõĖ¬ńŗ¼ń½ŗÕÅéµĢ░ŃĆéµ£ĆÕĖĖĶ¦üńÜäÕłåĶ¦Żµ¢╣µ│Ģµś»õĮ┐µĀćÕćå’╝łµĀćķćÅ’╝ēķ╗ÅÕ║”ÕÆīõĮōń¦»ķ╗ÅÕ║” Õģ│ń│╗õĖ║õ╗źÕÅŖ’╝īµ£Ćń╗łÕ£©ń¤óķćÅń¼”ÕÅĘõĖŁÕŠŚÕł░’╝Ü
ÕģČõĖŁµś»ÕŹĢõĮŹÕ╝ĀķćÅŃĆé[13]Ķ┐ÖõĖ¬µ¢╣ń©ŗÕÅ»ń£ŗõĮ£ńēøķĪ┐ķ╗ÅµĆ¦Õ«ÜÕŠŗńÜäÕ╣┐õ╣ēÕĮóÕ╝ÅŃĆé õĖĆõĖ¬ÕÅ»ÕÄŗń╝®µĄüõĮōĶó½ÕØćÕīĆÕÄŗń╝®µł¢µē®Õ▒ĢµŚČ’╝īµ▓Īµ£ēÕē¬Õłć’╝īõĮåÕ«āõ╗ŹńäČõ╗źÕåģķā©µæ®µō”ńÜäÕĮóÕ╝ÅĶĪ©ńÄ░µØźµŖĄÕłČÕ«āńÜ䵥üÕŖ©ŃĆéĶ┐Öõ║øÕŖøńÜäõĖĆõĖ¬õĖÄÕÄŗń╝®µł¢Ķå©ĶāĆńÄćµ£ēÕģ│ńÜäÕøĀń┤ĀŽā’╝īń¦░õĖ║õĮōń¦»ķ╗ÅÕ║”’╝īµł¢ń¼¼õ║īķ╗ÅÕ║”ŃĆéÕŬµ£ēÕĮōµĄüõĮōĶó½Ķ┐ģķƤÕÄŗń╝®µł¢µē®Õ▒ĢµŚČ’╝īÕ”éÕŻ░ķ¤│ÕÆīÕå▓Õć╗µ│ó’╝īõĮōń¦»ķ╗ÅÕ║”µśŠÕŠŚÕŠłķćŹĶ”üŃĆéõĮōń¦»ķ╗ÅÕ║”Ķ¦ŻķćŖõ║åĶ┐Öõ║øµ│óńÜäĶāĮķćŵŹ¤Õż▒’╝īµŁŻÕ”éµ¢»µēśÕģŗµ¢»ńÜäÕŻ░ĶĪ░ÕćÅĶ¦äÕŠŗµēƵÅÅĶ┐░ńÜäŃĆéõĮōń¦»ķ╗ÅÕ║”ĶĪ©ńż║õĖĆń¦ŹµŖĄµŖŚµĄüõĮōµŚĀÕē¬ÕłćÕÄŗń╝®µł¢Ķå©ĶāĆńÜäÕåģķā©µæ®µō”ŃĆéÕ£©µĄüõĮōÕŖ©ÕŖøÕŁ”ķŚ«ķóśõĖŁķĆÜÕĖĖõĖŹµś»Õ┐ģķ£ĆńÜäŃĆéõŠŗÕ”é’╝īõĖŹÕÅ»ÕÄŗń╝®µĄüõĮōµ╗ĪĶČ│ÕøĀµŁżõĖŹÕɽŃĆ鵣żÕż¢’╝īÕ»╣õ║ĵ░öõĮōµØźĶ»┤ķĆÜÕĖĖĶ«żõĖ║ÕÅ»Õ┐ĮńĢź’╝īÕøĀõĖ║Õ£©ÕŹĢÕÄ¤ÕŁÉńÉåµā│µ░öõĮōõĖŁµś»ŃĆé[13]ÕŬµ£ēÕĮōµĄüõĮōĶ┐ģķƤÕÄŗń╝®µł¢µē®Õ▒Ģ’╝īńö©µ¢»µēśÕģŗµ¢»ÕŻ░ķ¤│ĶĪ░ÕćÅÕ«ÜÕŠŗµØźµÅÅĶ┐░ÕŻ░ķ¤│ÕÆīÕå▓Õć╗µ│óµŚČ’╝īõĮōń¦»ķ╗ÅÕ║”µēŹµśŠÕŠŚÕŠłķćŹĶ”üŃĆé ķ╗ÅÕ║”ńÜäÕ«Üõ╣ēµ¢╣ń©ŗõĖŹµś»Ķć¬ńäČńĢīńÜäÕ¤║µ£¼Õ«ÜÕŠŗ’╝īÕøĀµŁżÕ«āõ╗¼ńÜäÕ«×ńö©µĆ¦õ╗źÕÅŖµĄŗķćŵł¢Ķ«Īń«Śķ╗ÅÕ║”ńÜäµ¢╣µ│ĢÕ┐ģķĪ╗õĮ┐ńö©ÕŹĢńŗ¼ńÜäµ¢╣µ│ĢµØźÕ╗║ń½ŗŃĆéõĖĆõĖ¬µĮ£Õ£©ńÜäķŚ«ķ󜵜»’╝īķ╗ÅÕ║”ÕÄ¤ÕłÖõĖŖÕÅ¢Õå│õ║ĵĄüõĮōńÜäÕ«īµĢ┤ÕŠ«Ķ¦éńŖȵĆü’╝īÕģČõĖŁÕīģµŗ¼ń│╗ń╗¤õĖŁµ»ÅõĖ¬ń▓ÆÕŁÉńÜäõĮŹńĮ«ÕÆīÕŖ©ķćÅŃĆé[15]Ķ┐Öń¦Źķ½śÕ║”Ķ»”ń╗åńÜäõ┐Īµü»ķĆÜÕĖĖõĖŹńÄ░Õ«×ŃĆéńäČĶĆī’╝īĶ┐Öõ║øõ┐Īµü»õĖŁńÜäÕż¦ķā©Õłåµ¤Éõ║øµØĪõ╗ČõĖŗÕÅ»õ╗źÕ┐ĮńĢźõĖŹĶ«ĪŃĆéńē╣Õł½µś»’╝īÕ»╣õ║ĵğĶ┐æÕ╣│ĶĪĪńŖȵĆüõĖöĶ┐£ń”╗ĶŠ╣ńĢī’╝łµ£¼õĮōńŖȵĆü’╝ēńÜäńēøķĪ┐µĄüõĮō’╝īķ╗ÅÕ║”õ╗ģÕÅ¢Õå│õ║ÄÕ«Üõ╣ēÕ▒Ćķā©Õ╣│ĶĪĪńÜäń®║ķŚ┤ÕÆīµŚČķŚ┤ńøĖÕģ│ńÜäÕ«ÅĶ¦éÕ£║’╝łÕ”éµĖ®Õ║”ÕÆīÕ»åÕ║”’╝ēŃĆé[15][16] Õ░Įń«ĪÕ”éµŁż’╝īķ╗ÅÕ║”õ╗ŹÕÅ»ĶāĮÕ»╣ÕżÜń¦Źń│╗ń╗¤ńē╣µĆ¦Õģʵ£ēõĖŹÕÅ»Õ┐ĮńĢźńÜäõŠØĶĄ¢µĆ¦’╝īõŠŗÕ”éµĖ®Õ║”ŃĆüÕÄŗÕŖøõ╗źÕÅŖõ╗╗õĮĢÕż¢ķā©Õ╝║Ķ┐½ńÜäÕ╣ģÕ║”ÕÆīķóæńÄćŃĆéÕøĀµŁż’╝īķ╗ÅÕ║”ńÜäń▓ŠńĪ«µĄŗķćÅõ╗ģķÆłÕ»╣ńē╣Õ«ÜńÜ䵥üõĮōńŖȵĆüĶ┐øĶĪīÕ«Üõ╣ēŃĆéõĖ║õ║åµĀćÕćåÕī¢Õ«×ķ¬īÕÆīńÉåĶ«║µ©ĪÕ×ŗõ╣ŗķŚ┤ńÜäµ»öĶŠā’╝īķ╗ÅÕ║”µĢ░µŹ«µ£ēµŚČõ╝ÜÕż¢µÄ©Õł░ńÉåµā│ńÜäµ×üķÖɵāģÕåĄ’╝īõŠŗÕ”éķøČÕē¬Õłćµ×üķÖɵł¢’╝łÕ»╣õ║ĵ░öõĮō’╝ēķøČÕ»åÕ║”µ×üķÖÉŃĆé ķ╗ÅÕ║”Õ╝ĀķćÅÕ£©õĖĆĶł¼µāģÕåĄõĖŗ’╝īµĄüÕŖ©õĖŁńÜäÕ║öÕŖøÕÅ»ķā©ÕłåÕĮÆÕøĀõ║Äõ╗Äõ╝æµü»ńŖȵĆüńÜäµØɵ¢ÖńÜäÕÅśÕĮó’╝łÕ╝╣µĆ¦Õ║öÕŖø’╝ē’╝īķā©ÕłåÕĮÆÕøĀõ║ÄÕÅśÕĮóķÜŵŚČķŚ┤ńÜäÕÅśÕī¢ńÄć’╝łķ╗ÅµĆ¦Õ║öÕŖø’╝ēŃĆéÕ£©µĄüõĮōõĖŁ’╝īµĀ╣µŹ«Õ«Üõ╣ē’╝īÕ╝╣µĆ¦Õ║öÕŖøõ╗ģÕīģµŗ¼ķØÖµ░┤ÕÄŗÕŖøŃĆéÕ£©õĖĆĶł¼ńÜäµ£»Ķ»ŁõĖŁ’╝īµĄüõĮōńÜäķ╗ÅÕ║”µś»Õ║öÕÅśńÄćÕÆīķ╗ÅµĆ¦Õ║öÕŖøõ╣ŗķŚ┤ńÜäÕģ│ń│╗ŃĆéÕ£©ńēøķĪ┐µĄüõĮōµ©ĪÕ×ŗ’╝īÕģ│ń│╗µś»ķĆÜĶ┐ćÕ«Üõ╣ēõĖĆõĖ¬ń║┐µĆ¦µśĀÕ░ä’╝īńö▒ķ╗ÅÕ║”Õ╝ĀķćŵÅÅĶ┐░’╝īõ╣śõ╗źÕ║öÕÅśńÄćÕ╝ĀķćÅ’╝łĶ┐Öµś»µĄüÕŖ©ńÜäķƤÕ║”µó»Õ║”’╝ē’╝īń╗ÖÕć║õ║åķ╗ÅµĆ¦Õ║öÕŖøÕ╝ĀķćÅŃĆéõĖĆĶł¼’╝īķ╗ÅÕ║”Õ╝ĀķćÅÕģʵ£ēõ╣ØõĖ¬ńŗ¼ń½ŗńÜäĶć¬ńö▒Õ║”ŃĆéÕÉäÕÉæÕÉīµĆ¦ńÜäńēøķĪ┐µĄüõĮō’╝īĶ┐ÖÕÅ»õ╗źÕćÅÕ░æÕł░õĖżõĖ¬ńŗ¼ń½ŗńÜäÕÅéµĢ░ŃĆéµ£ĆÕĖĖĶ¦üńÜ䵜»’╝īÕ║öÕŖøķ╗ÅÕ║”ÕÆīµ£¼õĮōķ╗ÅÕ║”ŃĆé ÕŖ©ķćÅĶŠōĶ┐ÉĶŠōĶ┐ÉńÉåĶ«║õ╗ÄÕŖ©ķćÅĶŠōĶ┐ÉńÜäĶ¦ÆÕ║”Õ»╣ķ╗ÅÕ║”Ķ┐øĶĪīõ║åÕÅ”õĖĆń¦ŹĶ¦ŻķćŖ’╝Üķ╗ÅÕ║”µś»ĶĪ©ÕŠüµĄüõĮōÕåģÕŖ©ķćÅõ╝ĀĶŠōńÜäµØɵ¢Öńē╣µĆ¦’╝īÕ░▒ÕāÅńāŁÕ»╝ńÄćĶĪ©ÕŠüńāŁĶŠōĶ┐É’╝ī’╝łĶ┤©ķćÅ’╝ēµē®µĢŻńÄćĶĪ©ÕŠüĶ┤©ķćÅĶŠōĶ┐ÉõĖƵĀĘŃĆé[13]Ķ┐Öń¦ŹĶ¦éńé╣ķÜÉÕɽգ©ńēøķĪ┐ķ╗ÅÕ║”Õ«ÜÕŠŗõĖŁ’╝ī’╝īÕøĀõĖ║Õē¬Õ║öÕŖøÕģČÕŹĢõĮŹńøĖÕĮōõ║ÄÕŖ©ķćÅķĆÜķćÅ’╝īÕŹ│ÕŹĢõĮŹµŚČķŚ┤ÕåģÕŹĢõĮŹķØóń¦»õĖŖńÜäÕŖ©ķćÅŃĆéÕøĀµŁż’╝īÕÅ»õ╗źĶ¦ŻķćŖõĖ║µīćÕ«ÜÕŖ©ķćŵĄüÕŖ©õ╗ÄõĖĆõĖ¬µĄüõĮōÕ▒éÕł░ÕÅ”õĖĆõĖ¬µĄüõĮōÕ▒éńÜäµ¢╣ÕÉæŃĆéµĀ╣µŹ«ńēøķĪ┐ķ╗ÅÕ║”Õ«ÜÕŠŗ’╝īĶ┐Öń¦ŹÕŖ©ķćŵĄüÕÅæńö¤Õ£©ķƤÕ║”µó»Õ║”õĖŖ’╝īńøĖÕ║öÕŖ©ķćÅķĆÜķćÅńÜäÕ╣ģÕ║”ńö▒ķ╗ÅÕ║”Õå│Õ«ÜŃĆé ÕÅ»õ╗źµśÄńĪ«Õ£░ń▒╗µ»öńāŁķćÅÕÆīĶ┤©ķćÅõ╝ĀķĆÆŃĆ鵣ŻÕ”éńāŁķćÅõ╗Äķ½śµĖ®µĄüÕÉæõĮĵĖ®ŃĆüĶ┤©ķćÅõ╗Äķ½śÕ»åÕ║”µĄüÕÉæõĮÄÕ»åÕ║”õĖƵĀĘ’╝īÕŖ©ķćÅõ╣¤õ╗Äķ½śķƤµĄüÕÉæõĮÄķƤŃĆéĶ┐Öõ║øĶĪīõĖ║ķāĮńö▒ń┤¦ÕćæńÜäĶĪ©ĶŠŠÕ╝ŵÅÅĶ┐░’╝īń¦░õĖ║µ£¼µ×äÕģ│ń│╗’╝īÕģČõĖĆń╗┤ÕĮóÕ╝ÅÕ”éõĖŗ’╝Ü ÕģČõĖŁµś»ķ╗ÅÕ║”’╝īÕÆīµś»Ķ┤©ķćÅÕÆīńāŁķĆÜķćÅ’╝īÕÆīµś»Ķ┤©ķćŵē®µĢŻńÄćÕÆīńāŁÕ»╝ńÄćŃĆé[17]Ķ┤©ķćÅŃĆüÕŖ©ķćÅÕÆīĶāĮķćÅ’╝łńāŁķćÅ’╝ēõ╝ĀĶŠōµś»Ķ┐×ń╗ŁÕŖøÕŁ”õĖŁµ£ĆńøĖÕģ│ńÜäĶ┐ćń©ŗ’╝īĶ┐ÖõĖĆõ║ŗÕ«×Õ╣ČķØ×ÕʦÕÉł’╝ÜĶ┐Öõ║øµś»ń▓ÆÕŁÉķŚ┤ńó░µÆ×õĖŁÕ£©ÕŠ«Ķ¦éÕ▒éķØóõĖŖÕ«łµüÆńÜäÕ░æµĢ░ńē®ńÉåķćÅŃĆéÕøĀµŁż’╝īÕ«āõ╗¼ńÜäÕŖ©µĆüõĖŹµś»ńö▒Õ┐½ķƤĶĆīÕżŹµØéńÜäÕŠ«Ķ¦éńøĖõ║ÆõĮ£ńö©µŚČķŚ┤Õ░║Õ║”Õå│Õ«ÜńÜä’╝īĶĆīµś»ÕÅæńö¤Õ£©Õ«ÅĶ¦éµŚČķŚ┤Õ░║Õ║”õĖŖ’╝īµŁŻÕ”éĶŠōĶ┐ÉńÉåĶ«║ÕÆīµĄüõĮōÕŖ©ÕŖøÕŁ”ńÜäÕÉäń¦Źµ¢╣ń©ŗµēƵÅÅĶ┐░ķ鯵ĀĘŃĆé ńēøķĪ┐µĄüõĮōõĖÄķØ×ńēøķĪ┐µĄüõĮōńēøķĪ┐µĄüõĮō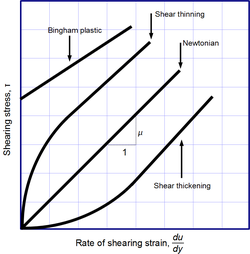 ńēøķĪ┐µĄüõĮōµś»ĶĪ©Ķ¦éķ╗ÅÕ║”õĖÄÕē¬ÕłćķƤńÄ浌ĀÕģ│ńÜ䵥üÕŖ©ńē╣µĆ¦ńÜ䵥üõĮō’╝łÕŹ│µ£Źõ╗ÄńēøķĪ┐ķ╗ÅµĆ¦Õ«ÜÕŠŗńÜ䵥üõĮō’╝ēŃĆéķ╗ÅµĆ¦Õ«ÜÕŠŗµś»õĖĆõĖ¬µ£¼µ×äµ¢╣ń©ŗ’╝īĶĆīõĖŹµś»õĖĆõĖ¬Ķć¬ńäȵ│ĢÕłÖŃĆéõĖĆń¦ŹµĄüõĮōńÜäĶĪīõĖ║ń¼”ÕÉłńēøķĪ┐Õ«ÜÕŠŗ’╝īķ╗ÅÕ║”ńŗ¼ń½ŗõ║ÄÕ║öÕŖøńÜäń¦░õĖ║ńēøķĪ┐µĄüõĮōŃĆéµ░öõĮō’╝īµ░┤ÕÆīĶ«ĖÕżÜÕĖĖĶ¦üńÜäµČ▓õĮōÕÅ»õ╗źÕ£©µÖ«ķĆÜńÜäµØĪõ╗ČÕÆīńÄ»ÕóāĶĆāĶÖæõĖ║ńēøķĪ┐µĄüõĮōŃĆé ńēøķĪ┐µĄüõĮōńÜ䵥üÕŖ©µø▓ń║┐’╝łÕē¬ÕłćÕ║öÕŖøõĖÄÕē¬ÕłćķƤńÄćńÜäÕģ│ń│╗µø▓ń║┐ń¦░õĖ║µĄüÕŖ©µø▓ń║┐’╝ē’╝īµś»õĖƵØĪķĆÜĶ┐ćÕĤńé╣ńÜäµ¢£ńø┤ń║┐’╝īĶ®▓µóص¢£ńø┤ń║┐ńÜäµ¢£ńÄćÕŹ│µś»Ķ®▓ńēøķĪ┐µĄüõĮōńÜäķ╗ÅÕ║”’╝īµ¢£ńÄćõĖŹÕÉī’╝īķ╗ÅÕ║”õĖŹÕÉīŃĆéÕ»╣õ║ÄÕÉīõĖƵĄüõĮō’╝īÕ£©õ╗╗õĮĢÕē¬ÕłćķƤńÄćõĖŗ’╝īķ╗ÅÕ║”ńøĖÕÉī’╝īõĖÄÕē¬ÕłćķƤńÄ浌ĀÕģ│ŃĆé ńē╣ķ▓üķĪ┐µ»öńÄ浜»µŗēõ╝Ėķ╗ÅÕ║”õĖÄÕē¬Õłćķ╗ÅÕ║”õ╣ŗµ»öŃĆéÕ»╣õ║ÄńēøķĪ┐µĄüõĮō’╝īńē╣ķ▓üķĪ┐µ»öńÄćõĖ║3ŃĆé[18][19] ķØ×ńēøķĪ┐µĄüõĮōķØ×ńēøķĪ┐µĄüõĮōµś»µśÄµśŠÕüÅń”╗ńēøķĪ┐Õ«ÜÕŠŗńÜ䵥üõĮō’╝īµ»öÕ”é’╝Ü
Õē¬Õłćń©ĆÕī¢µČ▓õĮōķĆÜÕĖĖĶó½µÅÅĶ┐░õĖ║Ķ¦”ÕÅśµĆ¦µČ▓õĮō’╝īõĮåĶ┐Öń¦ŹµÅÅĶ┐░Õ«╣µśōÕ╝ĢĶĄĘĶ»»Ķ¦ŻŃĆé[20] ÕŹ│õĮ┐µś»ńēøķĪ┐µĄüõĮō’╝īķ╗ÅÕ║”ķĆÜÕĖĖÕÅ¢Õå│õ║ÄÕģČń╗䵳ÉÕÆīµĖ®Õ║”ŃĆéµ░öõĮōńŁēÕÅ»ÕŻōńĖ«µĄü’╝īĶ┐ÖÕÅ¢Õå│õ║ĵĖ®Õ║”’╝īĶĆīķÜÅÕÄŗÕŖøÕÅśÕī¢ÕŠłµģóŃĆéõĖĆõ║øµĄüõĮōńÜäķ╗ÅÕ║”ÕÅ»ĶāĮÕÅ¢Õå│õ║ÄÕģČõ╗¢ÕøĀń┤ĀŃĆéõŠŗÕ”éńŻüµĄüÕÅśµĄüõĮō’╝īµĄüõĮōÕ£©ÕŖĀńŻüÕ£║ÕÉÄÕÅśÕÄÜ’╝īÕÅ»ĶāĮõ╝ÜĶĪ©ńÄ░ÕŠŚÕāÅÕø║õĮōńé╣ŃĆé µ║ȵČ▓ķ╗ÅÕ║”Õ»╣õ║ĵ║ȵČ▓’╝łÕ░żÕģȵś»ķ½śÕłåÕŁÉµ║ȵČ▓’╝ē’╝īÕĖĖńö©Õł░õ╗źõĖŗÕćĀń¦Źķ╗ÅÕ║”ŃĆé ńøĖÕ»╣ķ╗ÅÕ║”’╝łÕÅłń¦░ķ╗ÅÕ║”µ»ö’╝ēµś»µ║ȵČ▓’╝łµł¢ÕłåµĢŻńøĖ’╝ēńÜäķ╗ÅÕ║”╬ĘõĖĵ║ČÕēé’╝łµł¢Ķ┐×ń╗ŁńøĖ’╝ēńÜäķ╗ÅÕ║”╬Ę0õ╣ŗµ»ö’╝īÕŹ│’╝Ü Õó×µ»öķ╗ÅÕ║”’╝łÕÅłń¦░µ»öķ╗ÅÕ║”’╝ēµś»µ║ȵČ▓’╝łµł¢ÕłåµĢŻńøĖ’╝ēńÜäķ╗ÅÕ║”╬ĘõĖĵ║ČÕēé’╝łµł¢Ķ┐×ń╗ŁńøĖ’╝ēńÜäķ╗ÅÕ║”╬Ę0õ╣ŗÕĘ«Ķó½µ║ČÕēé’╝łµł¢Ķ┐×ń╗ŁńøĖ’╝ēķ╗ÅÕ║”ńÜä╬Ę0ķÖżÕŠŚõ╣ŗÕĢå’╝īÕŹ│’╝Ü µ»öµĄōķ╗ÅÕ║”’╝łÕÅłń¦░µŹóń«Śķ╗ÅÕ║”µł¢ķ╗ÅÕ║”µĢ░’╝ēµś»ÕŹĢõĮŹµĄōÕ║”ńÜäµ║ȵČ▓’╝łµł¢ÕłåµĢŻńøĖ’╝ēńÜäÕó×µ»öµĄōÕ║”’╝īÕŹ│’╝Ü µ»öµĄōÕ»╣µĢ░ķ╗ÅÕ║”’╝łÕÅłń¦░Õ»╣µĢ░ķ╗ÅÕ║”’╝ēµś»ńøĖÕ»╣ķ╗ÅÕ║”ńÜäĶć¬ńäČÕ»╣µĢ░Ķó½µ║ȵČ▓’╝łµł¢ÕłåµĢŻńøĖ’╝ēńÜ䵥ōÕ║”ķÖżÕŠŚõ╣ŗÕĢå’╝īÕŹ│’╝Ü ńē╣µĆ¦ķ╗ÅÕ║”’╝łÕÅłń¦░µ×üķÖÉķ╗ÅÕ║”’╝ēµś»µĄōÕ║”ĶČŗõ║ÄķøȵŚČµ»öµĄōķ╗ÅÕ║”ńÜäµ×üķÖÉÕĆ╝’╝īÕŹ│’╝Ü Õø║õĮōķ╗ÅÕ║”
 Õ£©µĄüõĮōµĄüÕŖ©õĖŁµēĆõ║¦ńö¤ńÜäķ╗ÅµĆ¦ÕŖøõĖŹĶāĮõĖÄÕ£©Õø║õĮōõĖŁÕ»╣Õē¬ÕłćŃĆüÕÄŗń╝®µł¢µŗēõ╝Ėõ║¦ńö¤ńÜäÕø×ÕżŹÕ╝╣µĆ¦ÕŖøńøĖµĘʵĘåŃĆéÕÉÄĶĆģńÜäÕ║öÕŖøµś»õĖÄÕĮóÕÅśķćŵłÉµ»öõŠŗńÜä’╝īĶĆīÕ£©µĄüõĮōõĖŁõĖÄÕĮóÕÅśķÜŵŚČķŚ┤ńÜäÕÅśÕī¢ńÄ浳ɵ»öõŠŗŃĆéńäČĶĆī’╝īĶ«ĖÕżÜµČ▓õĮō’╝łÕīģµŗ¼µ░┤’╝ēÕ£©ÕÅŚÕł░ń¬üńäČńÜäÕÄŗÕŖøÕÉÄ’╝īÕÅŹÕ║öÕāÅÕ╝╣µĆ¦Õø║õĮōŃĆéńøĖÕÅŹ’╝īńöÜĶć│Õ£©õ╗╗µäÅÕ║öÕŖøĶŠāÕ░Å’╝īĶ«ĖÕżÜŌĆ£Õø║õĮōŌĆØ’╝łÕŹ│õĮ┐ĶŖ▒Õ▓ŚÕ▓®’╝ēÕ░åÕāŵČ▓õĮōõĖƵĀʵĄüÕŖ©’╝īĶÖĮńäČÕŠłµģóŃĆéĶ┐ÖµĀĘńÜäµØɵ¢Ö’╝īÕģʵ£ēÕ╝╣µĆ¦’╝łÕÅŹÕ║öÕÅśÕĮó’╝ēÕÆīķ╗ÅÕ║”’╝łõ╗źÕÅśÕĮóńÄćńÜäÕÅŹÕ║ö’╝ē’╝īÕŹ│ķ╗ÅÕ╝╣µĆ¦ŃĆéķ╗ÅÕ╝╣µĆ¦Õø║õĮōÕÅ»ĶāĮĶĪ©ńÄ░Õć║ÕÄŗÕŖøķ╗ÅµĆ¦ÕÆīõĮōń¦»ķ╗ÅµĆ¦ŃĆéµŗēõ╝Ėķ╗ÅÕ║”ńÜäÕē¬ÕłćÕÆīõĮōń¦»ķ╗ÅÕ║”’╝īµÅÅĶ┐░õ║åõĖĆõĖ¬Õø║õĮōÕ╝╣µĆ¦µØɵ¢ÖńÜäõ╝ĖķĢ┐ńÄćńÜäÕÅŹÕ║öńÜäõĖĆõĖ¬ń║┐µĆ¦ń╗äÕÉł’╝īÕ«āÕ╣┐µ│øńö©õ║ÄĶĪ©ÕŠüĶüÜÕÉłńē®ŃĆéÕ£©Õ£░Ķ┤©ÕŁ”õĖŁ’╝īÕģʵ£ēķ╗ÅµĆ¦ÕÅśÕĮóĶć│Õ░æõĖēÕĆŹõ║ÄÕ╝╣µĆ¦ÕÅśÕĮóńÜäń©ĆÕ£¤µØɵ¢Öµ£ēµŚČĶó½ń¦░õĖ║µĄüÕÅśõĮōŃĆé ÕŹĢõĮŹÕŖ©ÕŖøķ╗ÅÕ║”ķ╗ÅÕ║”ńÜäÕøĮķÖģÕŹĢõĮŹÕłČµś»ÕĖĢµ¢»ÕŹĪ┬Ęń¦Æ[Pa┬Ęs]’╝īµ£ēµÖéõ╣¤õĮ┐ńö©õ╗źµ│ĢÕøĮńö¤ńÉåÕŁ”Õ«ČÕÉēµü®┬ĘĶĘ»µśōµ¢»┬ʵ│ŖĶéāÕÅČÕæĮÕÉŹńÜäµ│Ŗ[P]ŃĆéÕŹüõĖ¬µ│ŖńŁēõ║ÄõĖĆõĖ¬ÕĖĢµ¢»ÕŹĪ┬Ęń¦ÆŃĆé
Õ«×ķÖģõĖŖ’╝īµ£ēõĖżõĖ¬ķćÅĶó½ń¦░õĖ║ķ╗ÅÕ║”ŃĆéõĖŖķØóµēĆÕ«Üõ╣ēńÜäķćŵ£ēµŚČĶó½ń¦░õĖ║ÕŖ©µĆüķ╗ÅÕ║”ŃĆüń╗ØÕ»╣ķ╗ÅÕ║”µł¢ń«ĆÕŹĢķ╗ÅÕ║”’╝łµØźÕī║Õł½ÕģČõ╗¢ńÜäķćÅ’╝ē’╝īõĮåķĆÜÕĖĖõ╣¤ń¦░õĖ║ķ╗ÅÕ║”’╝īÕĖĖńö©ń¼”ÕÅĘõĖ║╬╝µł¢╬ĘŃĆéÕÅ”Õż¢õĖĆń¦ŹķćÅń¦░õĖ║Ķ┐ÉÕŖ©ķ╗ÅÕ║”’╝łńö©ń¼”ÕÅĘ╬ĮĶĪ©ńż║’╝ē’╝īÕ«āµś»µĄüõĮōńÜäķ╗ÅÕ║”õĖÄÕ»åÕ║”ńÜäµ»öÕĆ╝’╝Ü Ķ┐ÉÕŖ©ķ╗ÅÕ║”Ķ┐ÉÕŖ©ķ╗ÅÕ║”µś»Õ£©ķćŹÕŖøÕĮ▒ÕōŹõĖŗ’╝īĶĪĪķćŵŖĄÕłČµČ▓õĮōµĄüÕŖ©ńÜäķćÅŃĆéÕ«āńÜ䵥ŗķćÅĶŻģńĮ«ķĆÜÕĖĖĶó½ń¦░õĖ║µ»øń╗åń«Īķ╗ÅÕ║”Ķ«ĪŌĆöŌĆöÕ¤║µ£¼õĖŖµś»Õ║Ģķā©µ£ēõĖĆõĖ¬ńŗŁń¬äń«ĪńÜäµ£ēÕł╗Õ║”ńÜäńŁÆŃĆéÕĮōõĖżń¦ŹõĮōń¦»ńøĖÕÉīńÜäµČ▓õĮōµöŠńĮ«Õ£©ńøĖÕÉīńÜäµ»øń╗åń«ĪõĖŁ’╝īÕ╣ČõĖöÕÅ»õ╗źÕ£©ķćŹÕŖøńÜäÕĮ▒ÕōŹõĖŗµĄüÕŖ©’╝īķéŻõ╣łÕ£©µĄüĶ┐ćń«ĪķüōµŚČ’╝īķ╗ÅµĆ¦µĄüõĮōĶŖ▒Ķ┤╣ńÜ䵌ČķŚ┤µ»öÕ░æķ╗ÅµĆ¦µĄüõĮōĶŖ▒Ķ┤╣ńÜ䵌ČķŚ┤Ķ”üķĢ┐ŃĆéĶ┐ÉÕŖ©ķ╗ÅÕ║”ńÜäSIÕŹĢõĮŹµś»Õ╣│µ¢╣ń▒│/ń¦Æ’╝īµ▓Īµ£ēńē╣Õł½ńÜäÕÉŹÕŁŚŃĆéńö▒õ║ÄĶ┐ÖõĖ¬ÕŹĢõĮŹÕż¬Õż¦’╝īÕŠłÕ░æõĮ┐ńö©ŃĆéõĖĆõĖ¬µø┤ÕĖĖĶ¦üńÜäĶ┐ÉÕŖ©ķ╗ÅÕ║”ÕŹĢõĮŹµś»Õ╣│µ¢╣ÕÄśń▒│/ń¦Æ’╝īĶ┐Öµś»ĶĆāĶÖæÕł░õ╗źńł▒Õ░öÕģ░ńÜäµĢ░ÕŁ”Õ«ČÕÆīÕŖ©ńē®ÕŁ”Õ«Čõ╣öµ▓╗┬ĘÕŖĀÕĖāķćīÕ¤āÕ░ö┬ʵ¢»µēśÕģŗµ¢»’╝ł1819’Į×1903’╝ēĶĆīÕæĮÕÉŹńÜäµ¢»µēśÕģŗµ¢»’╝łSt’╝ēŃĆéĶ┐ÖõĖ¬ÕŹĢõĮŹõ╣¤µ£ēńé╣Õż¦’╝īµēĆõ╗źµ£ĆÕĖĖĶ¦üńÜäÕŹĢõĮŹÕÅ»ĶāĮµś»Õ╣│µ¢╣µ»½ń▒│/ń¦Æ’╝īµł¢ÕÄśÕÅĖŃĆé
ķ╗ÅÕ║”õĖĵĖ®Õ║”ńÜäÕģ│ń│╗õ╗ĵŚźÕĖĖń╗Åķ¬īõĖŁ’╝īÕÅ»õ╗źń¤źķüō’╝īķ╗ÅÕ║”ķÜÅńØƵĖ®Õ║”ńÜäÕÅśÕī¢ĶĆīÕÅśÕī¢ŃĆéÕ”é’╝īĶ£éĶ££ÕÆīń│¢µĄåÕ£©ÕŖĀńāŁµŚČµø┤Õ«╣µśōµĄüÕŖ©’╝øÕ£©Õå¼ÕŁŻÕż®µ░öÕÅśÕåʵŚČ’╝īÕÅæÕŖ©µ£║µČ”µ╗æµ▓╣ÕÆīµČ▓ÕÄŗµČ▓µśÄµśŠķ╗ÅµĆ¦Ķ«Ŗķ½ś’╝īõĖźķćŹÕĮ▒ÕōŹµ▒ĮĶĮ”ÕÅŖÕģČõ╗¢µ£║µó░ńÜäµĆ¦ĶāĮŃĆéõĖĆĶł¼µØźĶ»┤’╝īõĖĆń¦Źń«ĆÕŹĢµČ▓õĮōńÜäķ╗ÅÕ║”ķÜŵĖ®Õ║”ńÜäÕŹćķ½śĶĆīõĖŗķÖŹ’╝łÕÅŹõ╣ŗõ║”ńäČ’╝ē’╝īķÜÅńØƵĖ®Õ║”ńÜäÕŹćķ½ś’╝īµČ▓õĮōõĖŁÕłåÕŁÉõĖŁĶ┐ÉÕŖ©ńÜäÕ╣│ÕØćķƤÕ║”Õó×Õż¦’╝īõĖÄõĖ┤Ķ┐æÕłåÕŁÉńÜäµÄźĶ¦”µŚČķŚ┤ÕÅśń¤ŁŃĆéńĪ«ÕłćÕ£░Ķ»┤’╝īõĖżõĖ¬ÕÅśķćÅńÜäÕÅśÕī¢µś»ķØ×ń║┐µĆ¦ńÜä’╝īÕĮōµ£ēńøĖÕÅśÕÅæńö¤µŚČ’╝īÕÅśķćÅÕÅæńö¤ń¬üÕÅśŃĆé ÕŖĀńāŁµŚČ’╝īµČ▓õĮōµø┤µśōµĄüÕŖ©’╝īµ░öõĮōÕÅśń©ĀŃĆéµ░öõĮōńÜäķ╗ÅÕ║”ķÜŵĖ®Õ║”ńÜäÕŹćķ½śĶĆīÕó×Õż¦’╝īõĖöķ╗ÅÕ║”µŁŻµ»öõ║ĵĖ®Õ║”ńÜäÕ╣│µ¢╣µĀ╣ŃĆéĶ┐Öµś»ńö▒õ║ÄÕ£©µø┤ķ½śńÜäµĖ®Õ║”õĖŗ’╝īÕó×Õż¦õ║åÕłåÕŁÉķŚ┤ńó░µÆ×ńÜäķóæńÄćŃĆéÕøĀõĖ║µ░öõĮōõĖŁńÜäÕłåÕŁÉÕż¦ķā©ÕłåµŚČķŚ┤µś»Õ£©ń®║ķŚ┤Ķć¬ńö▒Ķ┐ÉÕŖ©’╝īõ╗╗õĮĢÕó×ÕŖĀõĖĆõĖ¬ÕłåÕŁÉõĖÄÕÅ”õĖĆõĖ¬ÕłåÕŁÉµÄźĶ¦”µŚČķŚ┤ńÜäÕøĀń┤Ā’╝īķāĮõ╝ÜķÖŹõĮÄÕłåÕŁÉõĮ£õĖ║õĖĆõĖ¬µĢ┤õĮōÕÅéõĖÄÕŹÅĶ░āĶ┐ÉÕŖ©ńÜäĶāĮÕŖøŃĆéĶ┐Öń▒╗ÕłåÕŁÉÕĮ╝µŁżÕÅæńö¤ńó░µÆ×’╝īĶ┐ÉÕŖ©ÕÅśÕŠŚµø┤ÕŖĀńÜäµØéõ╣▒µŚĀń½Ā’╝īÕģģÕłåĶ¦ŻķćŖõ║åµ░öõĮōķ╗ÅÕ║”Õ»╣µĖ®Õ║”ńÜäõŠØĶĄ¢µĆ¦ŃĆé ķ╗ÅÕ║”õĖĵĖ®Õ║”ńÜäÕģ│ń│╗ķØ×ÕĖĖÕ»åÕłć’╝īÕ£©ÕĖĖµĖ®ÕĖĖÕÄŗõĖŗ’╝īÕĮōµĖ®Õ║”ÕÅśÕī¢1ŌäāµŚČ’╝īµČ▓õĮōńÜäķ╗ÅÕ║”ÕÅśÕī¢ĶŠŠńÖŠÕłåõ╣ŗÕćĀĶć│ÕŹüÕćĀ’╝īµ░öõĮōń║”õĖ║ÕŹāÕłåõ╣ŗÕćĀ’╝īõŠŗÕ”éÕ£©’╝ł20┬▒1’╝ēŌäāµŚČµ£ē
ķ╗ÅÕ║”õĖĵĖ®Õ║”Õ╣ČõĖŹµłÉń║┐µĆ¦Õģ│ń│╗’╝īÕ«āõĖĵĖ®Õ║”ĶīāÕø┤µ£ēÕģ│’╝īµĖ®Õ║”ĶČŖõĮÄ’╝īķ╗ŵĖ®Õģ│ń│╗ĶČŖÕ»åÕłćŃĆéÕÅłÕ”é’╝īÕ£©0Ōäā’╝ī20ŌäāÕÅŖ100ŌäāõĖŗ’╝īÕĮō╬öT=┬▒1ŌäāµŚČ’╝īµ░┤ńÜäķ╗ÅÕ║”ÕÅśÕī¢’╝īÕłåÕł½ń║”õĖ║3.4%’╝ī2.5%ÕÅŖ1.1%[21]ŃĆ鵣żÕż¢’╝īµ░öõĮōõĖĵČ▓õĮōńÜäķ╗ÅÕ║”µĖ®Õ║”ÕÅśÕī¢ńÜäĶ¦äÕŠŗÕ«īÕģ©ńøĖÕÅŹ’╝īµ░öõĮōńÜäķ╗ÅÕ║”ķÜŵĖ®Õ║”ÕŹćķ½śĶĆīÕó×Õż¦’╝īÕøĀõĖ║µ░öõĮōńÜäķ╗ÅµĆ¦µś»ńö▒õ║ÄÕŖ©ķćÅõ╝ĀķĆƵēĆĶć┤’╝īÕĮōµĖ®Õ║”ÕŹćķ½śµŚČ’╝īÕłåÕŁÉńÜäńāŁĶ┐ÉÕŖ©ÕŖĀÕē¦’╝īÕŖ©ķćÅÕó×Õż¦’╝īµĄüÕ▒éķŚ┤ńÜäÕåģµæ®µō”ÕŖĀÕē¦’╝īµēĆõ╗źķ╗ÅÕ║”Õó×Õż¦ŃĆéĶĆīµČ▓õĮōńÜäķ╗ÅµĆ¦µØźĶć¬ÕłåÕŁÉÕ╝ĢÕŖø’╝īµĖ®Õ║”ÕŹćķ½ś’╝īÕłåÕŁÉķŚ┤ńÜäĶĘØń”╗ÕŖĀÕż¦’╝īÕłåÕŁÉÕ╝ĢÕŖøÕćÅÕ░Å’╝īÕåģµæ®µō”ÕćÅÕ╝▒’╝īµēĆõ╗źķ╗ÅÕ║”ÕćÅÕ░ÅŃĆé ķ╗ÅÕ║”ķÜŵĖ®Õ║”ÕÅśÕī¢ńÜäń©ŗÕ║”Ķ┐śõĖÄĶ«ĖÕżÜÕøĀń┤Āµ£ēÕģ│’╝īõŠŗÕ”éńē®Ķ┤©ńÜäÕī¢ÕŁ”ń╗䵳ÉŃĆüķ╗ŵĄüµ┤╗Õī¢ĶāĮŃĆüķ╗ÅÕ║”Õż¦Õ░ÅńŁē’╝īõŠŗÕ”éķĆÜÕĖĖµČ▓õĮōńÜäķ╗ÅÕ║”ĶČŖÕż¦’╝īµČ▓õĮōńÜäķ╗ÅÕ║”ķÜŵĖ®Õ║”ńÜäÕÅśÕī¢ĶČŖÕż¦ŃĆé ÕøĀõĖ║ķ╗ÅÕ║”µś»Õ”鵣żÕ£░õŠØĶĄ¢õ║ĵĖ®Õ║”’╝īµēĆõ╗źÕ£©µÅÅĶ┐░ķ╗ÅÕ║”µŚČń”╗õĖŹÕ╝ƵĖ®Õ║”ŃĆé ķ╗ÅÕ║”õĖÄÕÄŗÕŖøńÜäÕģ│ń│╗µ░öõĮōķ╗ÅÕ║”õĖÄÕÄŗÕ╝║ńÜäÕģ│ń│╗µ░öõĮōńÜäķ╗ÅÕ║”ķÜÅÕÄŗÕ╝║ńÜäÕó×Õż¦ĶĆīÕó×Õż¦’╝īķ╗ÅÕ║”õĖÄÕÄŗÕ╝║ńÜäÕģ│ń│╗ÕÅ»ńö▒Õģ¼Õ╝Å’╝ł’╝ēµ▒éÕŠŚ[22]ŃĆé µČ▓õĮōķ╗ÅÕ║”õĖÄÕÄŗÕŖøńÜäÕģ│ń│╗µČ▓õĮōķ╗ÅÕ║”ķÜÅÕÄŗÕŖøńÜäÕó×ÕŖĀĶĆīÕó×Õż¦’╝īõĮåĶ┐£õĖŹÕ”éµ░öõĮōńÜäķ╗ÅÕ║”õĖÄÕÄŗÕŖøńÜäÕģ│ń│╗õ╣ŗÕ»åÕłćŃĆéÕ£©500MPa’╝łÕŹ│5000Õż¦µ░öÕÄŗ’╝ēõĖŗ’╝īµČ▓õĮōķ╗ÅÕ║”õĖÄÕÄŗÕŖøńÜäÕģ│ń│╗ńö©Õģ¼Õ╝Å’╝ł’╝ēĶĪ©ńż║[22]ŃĆéµÖ«ķĆܵČ▓õĮōÕ£©0.1MPaķÖäĶ┐æ’╝īµ»ÅÕó×ÕŖĀ0.1MPaÕÄŗÕŖøµŚČ’╝īķ╗ÅÕ║”Õó×ÕŖĀń║”0.1%’Į×0.3%ŃĆéÕ»╣õ║Äķ╗ÅÕ║”╬Ę>1.2mPa┬ĘsńÜäµČ▓ńāā’╝īÕÅ»ńö©Õ║ōµ│ĮÕ░öÕ╝ÅµØźĶ«Īń«Śķ½śÕÄŗõĖŗńÜäķ╗ÅÕ║”ÕĆ╝ŃĆé ķ╗ÅÕ║”ńÜ䵥ŗķćŵĄŗķćÅķ╗ÅÕ║”ńÜäµ£ēÕÉäń¦Źķ╗ÅÕ║”Ķ«ĪÕÆīµĄüÕÅśõ╗¬ŃĆ鵥üÕÅśõ╗¬ńö©õ║ĵĄüõĮōńÜäķ╗ÅÕ║”õĖŹĶāĮńö©ÕŹĢõĖ¬ķ╗ÅÕ║”ÕĆ╝Õ«Üõ╣ēńÜäµāģÕåĄ ’╝īÕøĀµŁżĶ”üµ»öķ╗ÅÕ║”Ķ«Īķ£ĆĶ”üµø┤ÕżÜńÜäÕÅéµĢ░Ķ«ŠÕ«ÜÕÆīµĄŗķćÅŃĆéÕ░üķŚŁńÜ䵥üõĮōµĖ®Õ║”µÄ¦ÕłČµś»ÕćåńĪ«µĄŗķćŵēĆÕ┐ģÕżćńÜä’╝īńē╣Õł½µś»ÕāÅµČ”µ╗æµ▓╣ńÜäķ╗ÅÕ║”’╝īõ╗ģÕÅśÕī¢5ŌäāÕÅ»ń┐╗ÕĆŹŃĆéõĖĆõ║øµĄüõĮō’╝īÕ£©ĶŠāÕ«ĮńÜäÕē¬ÕłćķƤńÄćĶīāÕø┤Õåģ’╝īķ╗ÅÕ║”µś»µüÆÕ«ÜńÜä’╝łńēøķĪ┐µĄüõĮō’╝ēŃĆéµ▓Īµ£ēµüÆÕ«Üķ╗ÅÕ║”ńÜ䵥üõĮō’╝łķØ×ķ╗ÅÕ║”µĄüõĮō’╝ēõĖŹĶāĮńö▒ÕŹĢõĖĆńÜäµĢ░ÕŁŚµØźµÅÅĶ┐░ŃĆéķØ×ńēøķĪ┐µĄüõĮōĶĪ©ńÄ░Õć║Õē¬ÕłćÕ║öÕŖøÕÆīÕē¬ÕłćķƤńÄćõ╣ŗķŚ┤ÕÉäń¦ŹõĖŹÕÉīńÜäńøĖÕģ│µĆ¦ŃĆéńø«ÕēŹńö©ÕŠŚµ£ĆÕ╣┐µ│øńÜäõĖ╗Ķ”üµ£ēµ»øń╗åń«Īķ╗ÅÕ║”Ķ«Ī’╝īµŚŗĶĮ¼ķ╗ÅÕ║”Ķ«Ī’╝īĶÉĮńÉāķ╗ÅÕ║”Ķ«ĪÕÆīķöźµØ┐ķ╗ÅÕ║”Ķ«ĪńŁēÕćĀń¦Ź’╝īĶ┐Öõ║øõ╗¬ÕÖ©ÕÅ»õ╗źµĄŗķćÅ10-2’Į×1012µ│ŖńÜäķ╗ÅÕ║”ŃĆéÕÉäń¦Źķ╗ÅÕ║”Ķ«ĪµēĆķĆéÕ║öńÜäÕē¬ÕłćķƤńÄćĶīāÕø┤õĖŹÕÉīŃĆéµīżÕć║Õ╝ŵ»øń╗åń«Īķ╗ÅÕ║”Ķ«ĪķĆÜÕĖĖÕŻգ©10-1’Į×106õĖÄÕ«×ķÖģÕŖĀÕĘźµØĪõ╗ČķØ×ÕĖĖµÄźĶ┐æńÜäÕē¬ÕłćķƤńÄćĶīāÕø┤õĮ┐ńö©’╝øĶĮ¼ÕŖ©Õ╝Åķ╗ÅÕ║”Ķ«ĪÕÅ»ńö©õ║ÄÕē¬ÕłćķƤńÄćÕ£©10-3’Į×10ńÜäĶīāÕø┤’╝īĶĆīńÉāÕ╝Åķ╗ÅÕ║”Ķ«ĪÕŬĶāĮÕ£©ÕŠłõĮÄńÜäÕē¬ÕłćķƤńÄćĶīāÕø┤ÕåģõĮ┐ńö©ŃĆé µ¤Éõ║øńē╣Õ«Üńē®Ķ┤©ńÜäķ╗ÅÕ║”ń®║µ░ö ń®║µ░öńÜäķ╗ÅÕ║”õĖ╗Ķ”üÕÅ¢Õå│õ║ĵĖ®Õ║”ŃĆéÕ£©15 ┬░CµŚČ’╝īń®║µ░öńÜäķ╗ÅÕ║”µś»1.81├Ś10ŌłÆ5 kg/(m┬Ęs), 18.1 ╬╝Pa.s µł¢1.81├Ś10ŌłÆ5 Pa.sŃĆéÕ£©15 ┬░CµŚČń®║µ░öńÜäĶ┐ÉÕŖ©ķ╗ÅÕ║”µś»1.48├Ś10ŌłÆ5 m^2/sµł¢14.8 cStŃĆéÕ£©25 ┬░CµŚČ’╝īķ╗ÅÕ║”µś»18.6 ╬╝Pa.sÕÆīĶ┐ÉÕŖ©ķ╗ÅÕ║”µś»15.7 cStŃĆéõ║║õ╗¼ĶāĮõ╗ĵ░öõĮōķ╗ÅÕ║”Ķ«Īń«ŚÕÖ©õĖŖÕŠŚÕł░µ░öõĮōķ╗ÅÕ║”õĖĵĖ®Õ║”ńÜäÕćĮµĢ░ŃĆé µ░┤
ÕģČõĖŁA=2.414 ├Ś 10ŌłÆ5 Pa┬Ęs ; B = 247.8 K ; and C = 140 KŃĆé
µ│źµĄåĶ┐ÖõĖƵ£»Ķ»Łµé¼µĄ«µČ▓µÅÅĶ┐░ńÜ䵜»õ┐صīüńØƵĄüÕŖ©µĆ¦ńÜäµČ▓õĮōÕÆīÕø║õĮōķóŚń▓ÆńÜäµĘĘÕÉłńē®ŃĆéµĄåµ¢ÖńÜäķ╗ÅÕ║”ÕÅ»õ╗źĶó½µÅÅĶ┐░õĖ║ńøĖÕ»╣ńÜäµČ▓ńøĖķ╗ÅÕ║”’╝Ü Õ£©õ╗źõĖŖÕģ¼Õ╝ÅõĖŁ’╝ī╬╝sÕÆī╬╝lÕłåÕł½µś»µ│źµĄåÕÆīµČ▓õĮōńÜäÕŖ©ÕŖøķ╗ÅÕ║”’╝łPA┬ĘS’╝ē’╝ī╬╝rµś»ńøĖÕ»╣ķ╗ÅÕ║”’╝łµŚĀķćÅń║▓’╝ē µĀ╣µŹ«õĖŹÕÉīńÜäÕø║õĮōķóŚń▓ÆńÜäÕż¦Õ░ÅÕÆīµĄōÕ║”’╝īÕŁśÕ£©ÕćĀõĖ¬µ©ĪÕ×ŗ’╝īÕģȵÅÅĶ┐░ńøĖÕ»╣ķ╗ÅÕ║”ńÜäÕø║õĮōķóŚń▓ÆńÜäÕ╣ČÕģʵ£ēõĮōń¦»ÕłåµĢ░╔ĖÕŖ¤ĶāĮŃĆé Õ£©µ×üõĮĵĄōÕ║”ńÜäń╗åķóŚń▓ÆńÜäµāģÕåĄõĖŗ’╝īÕÅ»õ╗źõĮ┐ńö©ńł▒ÕøĀµ¢»ÕØ”µ¢╣ń©ŗ[23]’╝Ü Õ£©ķ½śµĄōÕ║”ńÜäµāģÕåĄõĖŗ’╝īńö▒Guth and SimhaµÅÉÕć║õ┐«µö╣ÕÉÄńÜäµ¢╣ń©ŗ[24]’╝īÕģČĶĆāĶÖæÕø║õĮōķóŚń▓Æõ╣ŗķŚ┤ńÜäńøĖõ║ÆõĮ£ńö©’╝īĶ┐ÖõĖ¬µ¢╣ń©ŗńÜäĶ┐øõĖƵŁźµö╣Ķ┐øńö▒µēśķ®¼µ¢»õ╗ÄÕ«×Ķ»üµĢ░µŹ«ńÜäµŗ¤ÕÉłõĖŁµÅÉÕć║ŃĆé ÕģČõĖŁA = 0.00273 and B = 16.6 Õ£©ķØ×ÕĖĖķ½śńÜ䵥ōÕ║”õĖŗ’╝īÕÅ”õĖĆõĖ¬ń╗Åķ¬īµ¢╣ń©ŗķĆÜĶ┐ćKitano ńŁēõ║║µÅÉÕć║ŃĆé:[25] ÕģČõĖŁÕ»╣õ║ÄÕģēµ╗æńÜäńÉāÕĮóķóŚń▓ÆA = 0.68ŃĆé ķØ×µÖȵĆüµØɵ¢Ö Õ£©ķØ×µÖȵØɵ¢ÖńÜäķ╗ÅµĆ¦µĄüÕŖ©’╝łÕ”éńÄ╗ńÆāÕÆīńåöõĮō’╝ēµś»õĖĆõĖ¬ńāŁµ┐Ƶ┤╗Ķ┐ćń©ŗ’╝Ü ÕģČõĖŁQµś»µ┤╗Õī¢ĶāĮ, Tµś»µĖ®Õ║”, RõĖ║µæ®Õ░öµ░öõĮōÕĖĖµĢ░ÕÆīAĶ┐æõ╝╝õĖ║õĖĆÕĖĖŃĆé Õ£©ķØ×µÖȵØɵ¢ÖńÜäķ╗ÅµĆ¦µĄüÕŖ©ńÜäńē╣ńé╣õĖÄķś┐õ╝”Õ░╝õ╣īµ¢»Õ╝ÅĶĪīõĖ║µ£ēÕüÅÕĘ«’╝ÜÕ£©ķ½śµĖ®õĖŗ’╝łÕ£©µČ▓õĮōńŖȵĆü’╝ē’╝īQÕÅśÕī¢õ╗ÄõĖĆõĖ¬Õ£©ĶŠāõĮĵĖ®Õ║”õĖŗ’╝łÕ£©ńÄ╗ńÆāµĆü’╝ēńÜäĶŠāķ½śÕĆ╝QHÕł░õĖĆõĖ¬ĶŠāķ½śµĖ®Õ║”õĖŗńÜäĶŠāõĮÄÕĆ╝QLŃĆéµĀ╣µŹ«Ķ┐ÖõĖĆÕÅśÕī¢’╝īµØźÕłÆÕłåķØ×µÖȵØɵ¢ÖŃĆé
ķØ×µÖȵØɵ¢ÖńÜäĶäåµĆ¦µś»µĢ░ÕĆ╝ńē╣ÕŠüńÜäÕżÜķøĘń▒│ńÜäĶäåÕ╝▒µĆ¦µ»ö’╝Ü ÕģČõĖŁ’╝īÕ╝║ńĪ¼ńÜäµØɵ¢ÖńÜäRD < 2ĶĆīĶäåµĆ¦µØɵ¢ÖńÜäRD Ōēź 2ŃĆé  ķØ×µÖȵØɵ¢ÖńÜäķ╗ÅÕ║”ńö▒ńö▒õĖĆõĖ¬õ║īµīćµĢ░µ¢╣ń©ŗńøĖÕĮōń▓ŠńĪ«Õ£░µÅÅĶ┐░’╝Ü ÕģČõĖŁÕīģµŗ¼ńÜäÕĖĖķćÅA1, A2, B, CÕÆīDõĖÄķØ×µÖȵØɵ¢ÖńÜäń╗ōÕÉłķö«ńÜäńāŁÕŖøÕŁ”ÕÅéµĢ░ńøĖÕģ│ŃĆé Õ”éµ×£µĖ®Õ║”Õ£©ńÄ╗ńÆāÕī¢ĶĮ¼ÕÅśµĖ®Õ║”ķÖäĶ┐æ’╝īTg,Ķ┐ÖõĖ¬µ¢╣ń©ŗÕÅ»õ╗źķĆÜĶ┐ćVogel-Fulcher-Tammann’╝łVFT’╝ēequationĶ┐æõ╝╝µ¢╣ń©ŗ’╝łVFT’╝ēĶĪ©ńż║ŃĆé Õ”éµ×£µĖ®Õ║”õĮÄõ║ÄńÄ╗ńÆāÕī¢ĶĮ¼ÕÅśµĖ®Õ║”’╝īT Ōē¬ Tg,ńäČÕÉÄõĖżõĖ¬µīćµĢ░µ¢╣ń©ŗń«ĆÕī¢õĖ║õĖĆõĖ¬ķś┐õ╝”Õ░╝õ╣īµ¢»Õ×ŗµ¢╣ń©ŗ’╝Ü Õ╣ČõĖö’╝Ü ÕģČõĖŁHdµś»µ¢Łķö«ńÜäÕĮóµłÉńäō’╝łń¦░õĖ║configuron S’╝ēÕÆīHm µś»ÕģČĶ┐ÉÕŖ©ńäōŃĆé ÕĮōµĖ®Õ║”õĮÄõ║ÄńÄ╗ńÆāÕī¢ĶĮ¼ÕÅśµĖ®Õ║”’╝īT < Tg’╝īÕģČķ╗ÅÕ║”ńÜäµ┤╗Õī¢ĶāĮķ½śÕøĀõĖ║ķØ×µÖȵØɵ¢ÖÕ£©ńÄ╗ńÆāµĆüÕÆīÕż¦ķā©Õłåń╗ōÕÉłķö«µś»Õ«īµĢ┤ńÜäŃĆé Õ”éµ×£µĖ®Õ║”µś»ķ½śÕ║”õ╗źõĖŖńÜäńÄ╗ńÆāÕī¢ĶĮ¼ÕÅśµĖ®Õ║”’╝īT Ōē½ Tg’╝īõĖżõĖ¬µīćµĢ░µ¢╣ń©ŗõ╣¤ń«ĆÕī¢õ║åõĖĆõĖ¬ķś┐õ╝”Õ░╝õ╣īµ¢»Õ×ŗµ¢╣ń©ŗ’╝Ü ĶĆīõĖö’╝Ü ÕĮōµĖ®Õ║”ķ½śõ║ÄńÄ╗ńÆāÕī¢ĶĮ¼ÕÅśµĖ®Õ║”’╝īT > Tg’╝īķ╗ÅÕ║”ńÜäµ┤╗Õī¢ĶāĮõĮÄ’╝īÕøĀõĖ║ķØ×µÖȵØɵ¢ÖĶó½ńåöÕī¢ÕÅŖÕģČÕż¦ķā©Õłåń╗ōÕÉłķö«µ¢ŁĶŻé’╝īĶ┐Öµ£ēÕł®õ║ĵĄüÕŖ©ŃĆé ÕģČõ╗¢ńē®Ķ┤©õĖŗĶĪ©ÕłŚÕć║õ║åõĖĆõ║øńēøķĪ┐µĄüõĮōńÜäĶ┐ÉÕŖ©ķ╗ÅÕ║”’╝Ü
*Ķ┐Öõ║øµØɵ¢Öµś»ķ½śµ┐āÕ║”ķØ×ńēøķĪ┐Õ×ŗńÜäŃĆé µ│©’╝Üķ½śµĄōÕ║”µäÅÕæ│ńØƵø┤ÕÄÜńÜäńē®Ķ┤©ŃĆé ÕÅéĶ¦üÕÅéĶĆāµ¢ćńī«
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia










![{\displaystyle [\mu ]={\frac {\rm {kg}}{\rm {m{\cdot }s}}}={\frac {\rm {N}}{\rm {m^{2}}}}{\cdot }{\rm {s}}={\rm {Pa{\cdot }s}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d184f591cc75d1b18bbfc0133e147646e360374a)





![{\displaystyle [\nu ]=\mathrm {\frac {m^{2}}{s}} =\mathrm {{\frac {N{\cdot }m}{kg}}{\cdot }s} =\mathrm {{\frac {J}{kg}}{\cdot }s} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3514532acd41448f56065fd8a7dad64cfafa63e2)














![{\displaystyle {\boldsymbol {\tau }}=\mu \left[\nabla \mathbf {v} +(\nabla \mathbf {v} )^{\mathrm {T} }\right]-\left({\frac {2}{3}}\mu -\kappa \right)(\nabla \cdot \mathbf {v} )\mathbf {\delta } }](https://wikimedia.org/api/rest_v1/media/math/render/svg/07beb6df9c134f304d74822aa6e3f1de320dd3fd)
















![{\displaystyle \left[\eta \right]=\lim _{c\to 0}{\frac {\eta _{sp}}{c}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40af9842071ed558a136f41c70515274a0abfbbb)



























