Pentellated 8-simplexes

8-simplex	Pentellated 8-simplex	Bipentitruncated 8-simplex
Orthogonal projections in A8 Coxeter plane

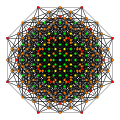
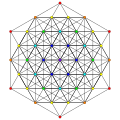
In eight-dimensional geometry, a pentellated 8-simplex is a convex uniform 8-polytope with 5th order truncations of the regular 8-simplex.

There are two unique pentellations of the 8-simplex. Including truncations, cantellations, runcinations, and sterications, there are 32 more pentellations. These polytopes are a part of a family 135 uniform 8-polytopes with A₈ symmetry. A₈, [3⁷] has order 9 factorial symmetry, or 362880. The bipentalled form is symmetrically ringed, doubling the symmetry order to 725760, and is represented the double-bracketed group [[3⁷]]. The A₈ Coxeter plane projection shows order [9] symmetry for the pentellated 8-simplex, while the bipentellated 8-simple is doubled to [18] symmetry.

Pentellated 8-simplex
Type	uniform 8-polytope
Schläfli symbol	t0,5{3,3,3,3,3,3,3}
Coxeter-Dynkin diagrams
7-faces
6-faces
5-faces
4-faces
Cells
Faces
Edges	5040
Vertices	504
Vertex figure
Coxeter group	A8, [37], order 362880
Properties	convex

Acronym: sotane (Jonathan Bowers)^[1]

The Cartesian coordinates of the vertices of the pentellated 8-simplex can be most simply positioned in 9-space as permutations of (0,0,0,0,1,1,1,1,2). This construction is based on facets of the pentellated 9-orthoplex.

orthographic projections

Ak Coxeter plane	A8	A7	A6	A5
Graph
Dihedral symmetry	[9]	[8]	[7]	[6]
Ak Coxeter plane	A4	A3	A2
Graph
Dihedral symmetry	[5]	[4]	[3]

Bipentellated 8-simplex
Type	uniform 8-polytope
Schläfli symbol	t1,6{3,3,3,3,3,3,3}
Coxeter-Dynkin diagrams
7-faces	t0,5{3,3,3,3,3,3}
6-faces
5-faces
4-faces
Cells
Faces
Edges	7560
Vertices	756
Vertex figure
Coxeter group	A8×2, [[37]], order 725760
Properties	convex, facet-transitive

• Small biterated bienneazetton
• Bipentellated enneazetton (Acronym: sobteb) (Jonathan Bowers)^[2]

The Cartesian coordinates of the vertices of the bipentellated 8-simplex can be most simply positioned in 9-space as permutations of (0,0,1,1,1,1,1,2,2). This construction is based on facets of the bipentellated 9-orthoplex.

orthographic projections

Ak Coxeter plane	A8	A7	A6	A5
Graph
Dihedral symmetry	[[9]] = [18]	[8]	[[7]] = [14]	[6]
Ak Coxeter plane	A4	A3	A2
Graph
Dihedral symmetry	[[5]] = [10]	[4]	[[3]] = [6]

Pentellated 8-simplex and dipentellated 8-simplex are two polytopes selected from 135 uniform 8-polytopes with A₈ symmetry.

A8 polytopes
t0	t1	t2	t3	t01	t02	t12	t03	t13	t23	t04	t14	t24	t34	t05
t15	t25	t06	t16	t07	t012	t013	t023	t123	t014	t024	t124	t034	t134	t234
t015	t025	t125	t035	t135	t235	t045	t145	t016	t026	t126	t036	t136	t046	t056
t017	t027	t037	t0123	t0124	t0134	t0234	t1234	t0125	t0135	t0235	t1235	t0145	t0245	t1245
t0345	t1345	t2345	t0126	t0136	t0236	t1236	t0146	t0246	t1246	t0346	t1346	t0156	t0256	t1256
t0356	t0456	t0127	t0137	t0237	t0147	t0247	t0347	t0157	t0257	t0167	t01234	t01235	t01245	t01345
t02345	t12345	t01236	t01246	t01346	t02346	t12346	t01256	t01356	t02356	t12356	t01456	t02456	t03456	t01237
t01247	t01347	t02347	t01257	t01357	t02357	t01457	t01267	t01367	t012345	t012346	t012356	t012456	t013456	t023456
t123456	t012347	t012357	t012457	t013457	t023457	t012367	t012467	t013467	t012567	t0123456	t0123457	t0123467	t0123567	t01234567

• H.S.M. Coxeter:
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, wiley.com, ISBN 978-0-471-01003-6
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
• Klitzing, Richard. "8D uniform polytopes (polyzetta) with acronyms". x3o3o3o3o3x3o3o – sotane, o3x3o3o3o3o3x3o – sobteb

• Polytopes of Various Dimensions
• Multi-dimensional Glossary