гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°
ж•°еӯҰгҒ«гҒҠгҒ„гҒҰгҖҒгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•° (гӮҜгғӘгғ•гӮ©гғјгғүгҒ гҒ„гҒҷгҒҶгҖҒиӢұ: Clifford algebra) гҒҜзөҗеҗҲеӨҡе…ғз’°гҒ®дёҖзЁ®гҒ§гҒӮгӮӢгҖӮK-д»Јж•°гҒЁгҒ—гҒҰгҖҒгҒқгӮҢгӮүгҒҜе®ҹж•°гҖҒиӨҮзҙ ж•°гҖҒеӣӣе…ғж•°гҖҒгҒқгҒ—гҒҰгҒ„гҒҸгҒӨгҒӢгҒ®д»–гҒ®и¶…иӨҮзҙ ж•°зі»гӮ’дёҖиҲ¬еҢ–гҒҷгӮӢ[1][2]гҖӮгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®зҗҶи«–гҒҜдәҢж¬ЎеҪўејҸгҒЁзӣҙдәӨеӨүжҸӣгҒ®зҗҶи«–гҒЁеҜҶжҺҘгҒӘй–ўдҝӮгҒҢгҒӮгӮӢгҖӮгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒҜе№ҫдҪ•еӯҰгҖҒзҗҶи«–зү©зҗҶеӯҰгҖҒгғҮгӮёгӮҝгғ«з”»еғҸеҮҰзҗҶгӮ’еҗ«гӮҖзЁ®гҖ…гҒ®еҲҶйҮҺгҒ«гҒҠгҒ„гҒҰйҮҚиҰҒгҒӘеҝңз”ЁгӮ’жҢҒгҒӨгҖӮгӮӨгӮ®гғӘгӮ№дәәе№ҫдҪ•еӯҰиҖ…гӮҰгӮЈгғӘгӮўгғ гғ»гӮӯгғігӮ°гғүгғігғ»гӮҜгғӘгғ•гӮ©гғјгғүгҒ«гҒЎгҒӘгӮ“гҒ еҗҚз§°гҒ§гҒӮгӮӢгҖӮ жңҖгӮӮгӮҲгҒҸзҹҘгӮүгӮҢгҒҹгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҖҒгҒӮгӮӢгҒ„гҒҜзӣҙдәӨгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•° (гҒЎгӮҮгҒЈгҒ“гҒҶгӮҜгғӘгғ•гӮ©гғјгғүгҒ гҒ„гҒҷгҒҶгҖҒиӢұ: orthogonal Clifford algebra) гҒҜгҖҒгғӘгғјгғһгғігӮҜгғӘгғ•гӮ©гғјгғүд»Јж•° (гғӘгғјгғһгғігӮҜгғӘгғ•гӮ©гғјгғүгҒ гҒ„гҒҷгҒҶгҖҒиӢұ: Riemannian Clifford algebra) гҒЁгӮӮе‘јгҒ°гӮҢгӮӢ[3]:83гҖӮ е°Һе…ҘгҒЁеҹәжң¬зҡ„жҖ§иіӘгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒҜдәҢж¬ЎеҪўејҸ Q гӮ’дјҙгҒЈгҒҹдҪ“ K дёҠгҒ®гғҷгӮҜгғҲгғ«з©әй–“ V гӮ’еҗ«гҒҝпјҢгҒқгӮҢгҒ«гӮҲгҒЈгҒҰз”ҹжҲҗгҒ•гӮҢгӮӢеҚҳдҪҚзҡ„зөҗеҗҲеӨҡе…ғз’°гҒ§гҒӮгӮӢгҖӮгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•° Cв„“(V, Q) гҒҜж¬ЎгҒ®жқЎд»¶гӮ’жәҖгҒҹгҒҷ V гҒӢгӮүз”ҹжҲҗгҒ•гӮҢгӮӢгҖҢжңҖгӮӮиҮӘз”ұгҒӘгҖҚд»Јж•°гҒ§гҒӮгӮӢ[жіЁйҮҲ 1]пјҡ гҒҹгҒ гҒ—е·ҰиҫәгҒ®з©ҚгҒҜгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒЁгҒ—гҒҰгҒ®з©ҚгҒ§гҒӮгӮҠгҖҒ1 гҒҜд№—жі•еҚҳдҪҚе…ғгҒ§гҒӮгӮӢгҖӮ гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®е®ҡзҫ©гҒҜгҖҢиЈёгҒ®гҖҚ(bare) K-д»Јж•°гӮҲгӮҠгӮӮеӨҡгҒҸгҒ®ж§ӢйҖ гӮ’гҒқгӮҢгҒ«дёҺгҒҲгӮӢпјҡ зү№гҒ«гҒқгӮҢгҒҜ V гҒ«еҗҢеһӢгҒӘзү№е®ҡгҒ®гҖҒгҒӮгӮӢгҒ„гҒҜзү№еҲҘгҒ«йҒёгҒ°гӮҢгҒҹйғЁеҲҶз©әй–“гӮ’жҢҒгҒӨгҖӮгҒқгҒ®гӮҲгҒҶгҒӘйғЁеҲҶз©әй–“гҒҜгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ«еҗҢеһӢгҒӘ K-д»Јж•°гҒ®гҒҝгҒҢдёҺгҒҲгӮүгӮҢгҒҰгӮӮдёҖиҲ¬гҒ«гҒҜдёҖж„ҸгҒ«гҒҜжұәгҒҫгӮүгҒӘгҒ„гҖӮ еҹәзӨҺдҪ“ K гҒ®жЁҷж•°гҒҢ 2 гҒ§гҒӘгҒ‘гӮҢгҒ°гҖҒгҒ“гҒ®еҹәжң¬й–ўдҝӮејҸгӮ’ж¬ЎгҒ®еҪўгҒ«жӣёгҒҚзӣҙгҒҷгҒ“гҒЁгҒҢгҒ§гҒҚгӮӢпјҡ гҒҹгҒ гҒ— гҒҜжҘөеҢ–жҒ’зӯүејҸ(polarization identity)гҒ«гӮҲгҒЈгҒҰ Q гҒЁзөҗгҒігҒӨгҒ„гҒҹеҜҫз§°еҸҢз·ҡеһӢеҪўејҸгҒ§гҒӮгӮӢгҖӮгҒ“гҒ®й–ўдҝӮејҸгӮ’жәҖгҒҹгҒҷгҖҢжңҖгӮӮиҮӘз”ұгҒӘгҖҚ (freest) гҒӮгӮӢгҒ„гҒҜгҖҢжңҖгӮӮдёҖиҲ¬гҖҚ (most general) гҒӘд»Јж•°гҒ§гҒӮгӮӢгҒ“гҒЁгҒ®гӮўгӮӨгғҮгӮўгҒҜжҷ®йҒҚжҖ§гҒ®жҰӮеҝөгӮ’йҖҡгҒҳгҒҰдёӢиЁҳгҒ§гҒ•гӮҢгӮӢгӮҲгҒҶгҒ«жӯЈејҸгҒ«иЎЁзҸҫгҒ§гҒҚгӮӢгҖӮ жЁҷж•° 2 гҒ®е ҙеҗҲгҒ®дәҢж¬ЎеҪўејҸгҒЁгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒҜдҫӢеӨ–зҡ„гҒӘе ҙеҗҲгҒ«гҒӘгӮӢгҖӮзү№гҒ«гҖҒchar(K) = 2 гҒ§гҒӮгӮҢгҒ°гҖҒдәҢж¬ЎеҪўејҸгҒҢеҜҫз§°еҸҢз·ҡеһӢеҪўејҸгӮ’жұәе®ҡгҒҷгӮӢгҒ“гҒЁгҖҒгҒӮгӮӢгҒ„гҒҜгҒҷгҒ№гҒҰгҒ®дәҢж¬ЎеҪўејҸгҒҢзӣҙдәӨеҹәеә•гӮ’жҢҒгҒӨгҒЁгҒ„гҒҶгҒ“гҒЁгҒҜжӯЈгҒ—гҒҸгҒӘгҒ„гҖӮгҒ“гҒ®иЁҳдәӢгҒ®гӮ№гғҶгғјгғҲгғЎгғігғҲгҒ®еӨҡгҒҸгҒҜжЁҷж•°гҒҢ 2 гҒ§гҒӘгҒ„гҒЁгҒ„гҒҶжқЎд»¶гӮ’еҗ«гҒҝгҖҒжқЎд»¶гҒҢйҷӨгҒӢгӮҢгӮӢгҒЁиӘӨгӮҠгҒ§гҒӮгӮӢгҖӮ еӨ–з©Қд»Јж•°гҒ®йҮҸеӯҗеҢ–гҒЁгҒ—гҒҰгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒҜеӨ–з©Қд»Јж•°гҒЁиҝ‘гҒ„й–ўдҝӮгҒ«гҒӮгӮӢгҖӮе®ҹгҒҜгҖҒQ = 0 гҒ§гҒӮгӮҢгҒ°гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•° Cв„“(V, Q) гҒҜгҒЎгӮҮгҒҶгҒ©еӨ–з©Қд»Јж•° вӢҖ(V) гҒ«гҒӘгӮӢгҖӮйӣ¶гҒ§гҒҜгҒӘгҒ„ Q гҒ«еҜҫгҒ—гҒҰеҹәзӨҺдҪ“ K гҒ®жЁҷж•°гҒҢ 2 гҒ§гҒӘгҒ„гҒЁгҒҚгҒ«гҒҜгҒ„гҒӨгҒ§гӮӮ вӢҖ(V) гҒЁ Cв„“(V, Q) гҒ®й–“гҒ®иҮӘ然гҒӘгҖҢз·ҡеһӢгҖҚеҗҢеһӢгҒҢеӯҳеңЁгҒҷгӮӢгҖӮгҒӨгҒҫгӮҠгҖҒгҒқгӮҢгӮүгҒҜгғҷгӮҜгғҲгғ«з©әй–“гҒЁгҒ—гҒҰиҮӘ然гҒ«еҗҢеһӢгҒ§гҒӮгӮӢгҒҢгҖҒз•°гҒӘгӮӢд№—жі•гӮ’дёҺгҒҲгӮӢпјҲжЁҷж•° 2 гҒ®е ҙеҗҲгҒ«гҒҜгҒқгӮҢгӮүгҒҜгҒӘгҒҠгғҷгӮҜгғҲгғ«з©әй–“гҒЁгҒ—гҒҰеҗҢеһӢгҒ§гҒӮгӮӢгҒҢгҖҒиҮӘ然гҒ«гҒ§гҒҜгҒӘгҒ„пјүгҖӮжҢҮе®ҡгҒ•гӮҢгҒҹйғЁеҲҶз©әй–“гҒЁгӮҜгғӘгғ•гӮ©гғјгғүд№—жі•гӮ’еҗҲгӮҸгҒӣгҒҹгӮӮгҒ®гҒҜгҒқгҒ®еҶ…е®№гҒҢеӨ–з©Қд»Јж•°гҒ«гҒҸгӮүгҒ№гӮӢгҒҰзңҹгҒ«гӮҲгӮҠиұҠгҒӢгҒ§гҒӮгӮӢгҖҒгҒӘгҒңгҒӘгӮүгҒ° Q гҒҢгӮӮгҒҹгӮүгҒҷиҝҪеҠ гҒ®жғ…е ұгӮ’дҪҝгҒҶгҒӢгӮүгҒ§гҒӮгӮӢгҖӮ гӮҲгӮҠжӯЈзўәгҒ«гҒҜгҖҒгғҜгӮӨгғ«д»Јж•°гҒҢеҜҫз§°д»Јж•°гҒ®йҮҸеӯҗеҢ–гҒ§гҒӮгӮӢгҒ®гҒЁеҗҢгҒҳж–№жі•гҒ§гҖҒгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒҜеӨ–з©Қд»Јж•°гҒ®йҮҸеӯҗеҢ–пјҲcf. йҮҸеӯҗзҫӨпјүгҒ§гҒӮгӮӢгҒЁиҖғгҒҲгӮӢгҒ“гҒЁгҒҢгҒ§гҒҚгӮӢгҖӮ гғҜгӮӨгғ«д»Јж•°гҒЁгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ§гҒҜгҒ•гӮүгҒ« *-з’°гҒЁгҒ„гҒҶж§ӢйҖ гӮ’жҢҒгҒЎгҖҒCCR and CAR algebras гҒ«гҒҠгҒ„гҒҰиӯ°и«–гҒ•гӮҢгҒҰгҒ„гӮӢгӮҲгҒҶгҒ«гҖҒи¶…д»Јж•°гҒ®еҒ¶й …гҒЁеҘҮй …гҒЁгҒ—гҒҰзөұдёҖгҒ§гҒҚгӮӢгҖӮ жҷ®йҒҚзҡ„гҒӘжҖ§иіӘгҒЁж§ӢжҲҗV гӮ’дҪ“ K дёҠгҒ®гғҷгӮҜгғҲгғ«з©әй–“гҒЁгҒ—гҖҒQ: V вҶ’ K гӮ’ V дёҠгҒ®дәҢж¬ЎеҪўејҸгҒЁгҒҷгӮӢгҖӮиҲҲе‘ігҒ®гҒӮгӮӢгҒҹгҒ„гҒҰгҒ„гҒ®гӮұгғјгӮ№гҒ§гҒҜдҪ“ K гҒҜе®ҹж•°дҪ“ R гҒӢиӨҮзҙ ж•°дҪ“ C гҒӢжңүйҷҗдҪ“гҒ§гҒӮгӮӢгҖӮ гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•° Cв„“(V, Q) гҒҜж¬ЎгҒ®жҷ®йҒҚжҖ§гҒ«гӮҲгҒЈгҒҰе®ҡзҫ©гҒ•гӮҢгӮӢгҒҷгҒ№гҒҰгҒ® v вҲҲ V гҒ«еҜҫгҒ—гҒҰ i(v)2 = Q(v)1 гӮ’жәҖгҒҹгҒҷз·ҡеһӢеҶҷеғҸ i : V вҶ’ Cв„“(V, Q) гӮ’дјҙгҒЈгҒҹ K дёҠгҒ®еҚҳдҪҚзҡ„зөҗеҗҲеӨҡе…ғз’°гҒ§гҒӮгӮӢпјҡ K дёҠгҒ®д»»ж„ҸгҒ®зөҗеҗҲд»Јж•° A гҒЁ
пјҲгҒҹгҒ гҒ— 1A гҒҜ A гҒ®д№—жі•еҚҳдҪҚе…ғгӮ’иЎЁгҒҷпјүгҒӘгӮӢд»»ж„ҸгҒ®з·ҡеһӢеҶҷеғҸ j : V вҶ’ A гҒҢдёҺгҒҲгӮүгӮҢгӮӢгҒЁгҖҒж¬ЎгҒ®еӣіејҸгҒҢдәӨжҸӣгҒҷгӮӢдёҖж„Ҹзҡ„гҒӘеӨҡе…ғз’°жә–еҗҢеһӢ f : Cв„“(V, Q) вҶ’ A пјҲгҒҷгҒӘгӮҸгҒЎ f вҲҳ i = jпјүгҒҢеӯҳеңЁгҒҷгӮӢпјҡ 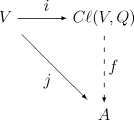 пјҲжЁҷж•°вү 2 гҒ«гҒҠгҒ„гҒҰпјүQ гҒ®д»ЈгӮҸгӮҠгҒ«еҜҫз§°еҸҢз·ҡеһӢеҪўејҸ вҹЁВ·,В·вҹ© гҒ§иҖғгҒҲгӮӢгҒЁгҖҒj гҒ«еҜҫгҒҷгӮӢиҰҒжұӮгҒҜж¬ЎгҒ®гӮҲгҒҶгҒ«гҒӘгӮӢгҖӮ дёҠгҒ§иЁҳиҝ°гҒ•гӮҢгҒҹжҖ§иіӘгӮ’гӮӮгҒӨгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒҜгҒӨгҒӯгҒ«еӯҳеңЁгҒ—гҒҰж¬ЎгҒ®гӮҲгҒҶгҒ«ж§ӢжҲҗгҒ§гҒҚгӮӢпјҡ V гӮ’еҗ«гӮҖжңҖгӮӮдёҖиҲ¬зҡ„гҒӘд»Јж•°гҖҒгҒҷгҒӘгӮҸгҒЎгғҶгғігӮҪгғ«д»Јж•° T(V) гҒ§е§ӢгӮҒгҖҒгҒқгӮҢгҒӢгӮүйҒ©еҲҮгҒӘе•ҶгӮ’еҸ–гӮӢгҒ“гҒЁгҒ«гӮҲгҒЈгҒҰеҹәжң¬й–ўдҝӮејҸгҒҢжҲҗгӮҠз«ӢгҒӨгӮҲгҒҶгҒ«гҒҷгӮӢгҖӮгҒ“гҒ®е ҙеҗҲ гҒ®еҪўгҒ®гҒҷгҒ№гҒҰгҒ®е…ғгҒ«гӮҲгҒЈгҒҰз”ҹжҲҗгҒ•гӮҢгҒҹ T(V) гҒ®дёЎеҒҙгӮӨгғҮгӮўгғ« IQ гӮ’еҸ–гӮҠйҷӨгҒҸгҒҹгӮҒгҒ«гҖҒCв„“(V, Q) гӮ’е•Ҷд»Јж•°
гҒЁгҒ—гҒҰе®ҡзҫ©гҒҷгӮӢгҖӮгҒ“гҒ®е•ҶгҒ«гӮҲгҒЈгҒҰз¶ҷжүҝгҒ•гӮҢгӮӢз’°гҒ®з©ҚгҒҜгҒЁгҒҚгҒ©гҒҚгӮҜгғӘгғ•гӮ©гғјгғүз©Қ (Clifford product) гҒЁе‘јгҒ°гӮҢ[4] еӨ–з©ҚгӮ„гӮ№гӮ«гғ©гғјз©ҚгҒӘгҒ©гҒЁгҒҜеҲҘгҒ®гӮӮгҒ®гҒЁгҒ—гҒҰеҢәеҲҘгҒ•гӮҢгӮӢгҖӮ гҒҷгӮӢгҒЁ Cв„“(V, Q) гҒҜ V гӮ’еҗ«гҒҝгҒӢгҒӨдёҠгҒ®жҷ®йҒҚжҖ§иіӘгӮ’жәҖгҒҹгҒҷгҒ“гҒЁгҒҢзӣҙгҒЎгҒ«зӨәгҒӣгҒҰгҒқгҒ®гҒ“гҒЁгҒӢгӮү Cв„“ гҒҜеҗҢеһӢгӮ’йҷӨгҒ„гҒҰдёҖж„ҸгҒ«жұәгҒҫгӮӢпјӣ гӮҸгӮҢгӮҸгӮҢгҒҢ "the" Clifford algebra Cв„“(V, Q) гҒЁгҒ„гҒҶгҒЁгҒҚгҒҜгҒқгҒ®гӮҲгҒҶгҒӘж„Ҹе‘ігҒ§гҒӮгӮӢгҖӮгҒ“гҒ®ж§ӢжҲҗгҒӢгӮү i гҒҢеҚҳе°„гҒ§гҒӮгӮӢгҒ“гҒЁгӮӮеҫ“гҒҶгҖӮйҖҡеёёгҒҜ V гӮ’ Cв„“(V, Q) гҒ®йғЁеҲҶз·ҡеһӢз©әй–“гҒ§гҒӮгӮӢгӮҲгҒҶгҒ«иҖғгҒҲгҒҰ i гӮ’жӣёгҒӢгҒҡгҒ«зңҒгҒҸгҖӮ дёҠиЁҳгҒ®гӮҲгҒҶгҒӘгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®жҷ®йҒҚзҡ„гҒӘзү№еҫҙгҒҘгҒ‘гҒҜ Cв„“(V, Q) гҒ®ж§ӢжҲҗгҒҢдәӢе®ҹдёҠй–ўжүӢзҡ„гҒ§гҒӮгӮӢгҒ“гҒЁгӮ’зӨәгҒ—гҒҰгҒ„гӮӢгҖӮгҒҷгҒӘгӮҸгҒЎгҖҒCв„“ гҒҜдәҢж¬ЎеҪўејҸгӮ’жҢҒгҒЈгҒҹгғҷгӮҜгғҲгғ«з©әй–“гҒ®еңҸпјҲе°„гҒҜдәҢж¬ЎеҪўејҸгӮ’дҝқгҒӨз·ҡеһӢеҶҷеғҸпјүгҒӢгӮүзөҗеҗҲд»Јж•°гҒёгҒ®й–ўжүӢгҒЁиҖғгҒҲгӮӢгҒ“гҒЁгҒҢгҒ§гҒҚгӮӢгҖӮжҷ®йҒҚжҖ§гҒҜпјҲдәҢж¬ЎеҪўејҸгӮ’дҝқгҒӨпјүгғҷгӮҜгғҲгғ«з©әй–“гҒ®й–“гҒ®з·ҡеһӢеҶҷеғҸгӮ’зөҗеҗҲгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®й–“гҒ®д»Јж•°жә–еҗҢеһӢгҒЁгҒ—гҒҰдёҖж„ҸгҒ«жӢЎејөгҒ§гҒҚгӮӢгҒ“гҒЁгӮ’дҝқиЁјгҒҷгӮӢгҖӮ еҹәеә•гҒЁж¬Ўе…ғгғҷгӮҜгғҲгғ«з©әй–“V гҒ®дҪ“ K дёҠгҒ®ж¬Ўе…ғгҒҢ n гҒ§гҒӮгӮҠ {e1, вҖҰ, en} гҒҢ (V, Q) гҒ®зӣҙдәӨеҹәеә•гҒ§гҒӮгӮҢгҒ°гҖҒ гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•° Cв„“(V, Q) гҒҜ K дёҠиҮӘз”ұгҒ§гҒқгҒ®еҹәеә•пјҲгҒ® 1 гҒӨпјүгҒҜд»ҘдёӢгҒ§дёҺгҒҲгӮүгӮҢгӮӢгҖӮ
з©әз©Қ (k = 0) гҒҜд»Јж•°гҒ®д№—жі•гҒ®еҚҳдҪҚе…ғгҒЁгҒ—гҒҰе®ҡзҫ©гҒ•гӮҢгӮӢгҖӮk гҒ®еҗ„еҖӨгҒ«еҜҫгҒ—гҒҰ еҖӢгҒ®еҹәеә•е…ғгҒҢеӯҳеңЁгҒҷгӮӢгҖҒгҒ—гҒҹгҒҢгҒЈгҒҰгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®з·Ҹж¬Ўе…ғгҒҜ V гҒҜдәҢж¬ЎеҪўејҸгӮ’дјҙгҒЈгҒҰгҒ„гӮӢгҒ®гҒ§гҖҒV гҒ® зү№еҲҘгҒӘеҹәеә•гҒЁгҒ—гҒҰзӣҙдәӨеҹәеә•гӮ’йҒёгҒ№гӮӢгҖӮзӣҙдәӨеҹәеә• гҒҜ
гҒ§гҒӮгӮӢгӮҲгҒҶгҒӘеҹәеә•гҒ§гҒӮгӮӢгҖӮгҒҹгҒ гҒ— вҹЁ-, -вҹ© гҒҜ Q гҒ«дјҙгҒҶеҜҫз§°еҸҢз·ҡеһӢеҪўејҸгҒ§гҒӮгӮӢгҖӮеҹәжң¬гӮҜгғӘгғ•гӮ©гғјгғүй–ўдҝӮејҸгҒЁгҒҜгҒ“гҒ®зӣҙдәӨеҹәеә•гҒ«еҜҫгҒҷгӮӢз©ҚгҒҢ гҒ§гҒӮгӮӢгҒ“гҒЁгӮ’ж„Ҹе‘ігҒ—гҒҰгҒ„гӮӢгҖӮгҒ“гҒ®гҒ“гҒЁгҒ«гӮҲгӮҠзӣҙдәӨеҹәеә•гғҷгӮҜгғҲгғ«гҒ®жүұгҒ„гҒҜжҘөгӮҒгҒҰз°ЎеҚҳгҒ«гҒӘгӮӢгҖӮV гҒ®зӣёз•°гҒӘгӮӢзӣҙдәӨеҹәеә•гғҷгӮҜгғҲгғ«гҒ®з©Қ гҒҢдёҺгҒҲгӮүгӮҢгҒҹгҒЁгҒҚгҖҒгҒқгӮҢгӮ’еҹәеә•гҒ®ж·»еӯ—гҒҢжЁҷжә–гҒ®й ҶеәҸгҒ«гҒӘгӮӢгӮҲгҒҶгҒ«дёҰгҒ№жӣҝгҒҲгӮӢгҒ“гҒЁгҒҜгҖҒгҒқгӮҢгҒ«еҝ…иҰҒгҒӘдәҢе…ғгҒ”гҒЁгҒ®е…ҘгӮҢжӣҝгҒҲгҒ®еӣһж•°гҒ«гӮҲгӮҠжұәгҒҫгӮӢз¬ҰеҸ·пјҲгҒҷгҒӘгӮҸгҒЎж•ҙеҲ—гҒ•гҒӣгӮӢгҒҹгӮҒгҒ®зҪ®жҸӣгҒ®з¬ҰеҸ·пјүгӮ’д»ҳгҒ‘гӮҢгҒ°гҒ§гҒҚгӮӢгҖӮ дҫӢпјҡ е®ҹгҒҠгӮҲгҒіиӨҮзҙ гҒ®гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°жңҖгӮӮйҮҚиҰҒгҒӘгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒҜйқһйҖҖеҢ–2ж¬ЎеҪўејҸгӮ’еӮҷгҒҲгҒҹе®ҹгҒҠгӮҲгҒіиӨҮзҙ гғҷгӮҜгғҲгғ«з©әй–“дёҠгҒ®гӮӮгҒ®гҒ§гҒӮгӮӢгҖӮ д»Јж•° Cв„“p,q(R) гҒЁ Cв„“n(C) гҒ®еҗ„гҖ…гҒҜ A гҒӮгӮӢгҒ„гҒҜ A вҠ• A гҒ«еҗҢеһӢгҒ§гҒӮгӮӢгҖҒгҒҹгҒ гҒ— A гҒҜжҲҗеҲҶгҒҢ R, C гҒӮгӮӢгҒ„гҒҜ H гҒӢгӮүжқҘгӮӢе…ЁиЎҢеҲ—з’°гҖҒгҒЁгҒ„гҒҶгҒ“гҒЁгҒҢжҳҺгӮүгҒӢгҒ«гҒӘгӮӢгҖӮгҒ“гӮҢгӮүгҒ®д»Јж•°гҒ®е®Ңе…ЁгҒӘеҲҶйЎһгҒҜгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®еҲҶйЎһгӮ’иҰӢгӮҲгҖӮ е®ҹдҝӮж•°гҒ®е ҙеҗҲвҶ’и©ізҙ°гҒҜгҖҢе№ҫдҪ•д»Јж•°гҖҚгӮ’еҸӮз…§
е®ҹгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®е№ҫдҪ•еӯҰзҡ„гҒӘи§ЈйҮҲгҒҜе№ҫдҪ•д»Јж•°гҒЁгҒ—гҒҰзҹҘгӮүгӮҢгҒҰгҒ„гӮӢгҖӮ жңүйҷҗж¬Ўе…ғе®ҹгғҷгӮҜгғҲгғ«з©әй–“дёҠгҒ®гҒҷгҒ№гҒҰгҒ®йқһйҖҖеҢ–2ж¬ЎеҪўејҸгҒҜжЁҷжә–еҜҫи§’еҪўејҸ гҒ«еҗҢеҖӨгҒ§гҒӮгӮӢгҖҒгҒҹгҒ гҒ— n = p + q гҒҜгғҷгӮҜгғҲгғ«з©әй–“гҒ®ж¬Ўе…ғгҒ§гҒӮгӮӢгҖӮж•ҙж•°гҒ®зө„ (p, q) гҒҜдәҢж¬ЎеҪўејҸгҒ®з¬ҰеҸ·ж•°гҒЁе‘јгҒ°гӮҢгӮӢгҖӮгҒ“гҒ®дәҢж¬ЎеҪўејҸгӮ’жҢҒгҒЈгҒҹе®ҹгғҷгӮҜгғҲгғ«з©әй–“гҒҜгҒ—гҒ°гҒ—гҒ° Rp,q гҒЁиЎЁиЁҳгҒ•гӮҢгӮӢгҖӮRp,q дёҠгҒ®гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒҜ Cв„“p,q(R) гҒЁиЎЁиЁҳгҒ•гӮҢгӮӢгҖӮиЁҳеҸ· Cв„“n(R) гҒҜи‘—иҖ…гҒҢжӯЈе®ҡеҖӨгҒЁдёҚе®ҡеҖӨгҒ®з©әй–“гҒ©гҒЎгӮүгӮ’еҘҪгӮҖгҒӢгҒ«гӮҲгҒЈгҒҰ Cв„“n,0(R) гҒӮгӮӢгҒ„гҒҜ Cв„“0,n(R) гӮ’ж„Ҹе‘ігҒҷгӮӢгҖӮ Rp,q гҒ®жЁҷжә–жӯЈиҰҸзӣҙдәӨеҹәеә• (ei) гҒҜдә’гҒ„гҒ«зӣҙдәӨгҒҷгӮӢ n = p + q еҖӢгҒ®гғҷгӮҜгғҲгғ«гҒӢгӮүгҒӘгӮҠгҖҒгҒқгҒ®гҒҶгҒЎ p еҖӢгҒҜгғҺгғ«гғ +1 гӮ’жҢҒгҒЎгҖҒq еҖӢгҒҜгғҺгғ«гғ вҲ’1 гӮ’жҢҒгҒӨгҖӮд»Јж•° Cв„“p,q(R) гҒҜеҫ“гҒЈгҒҰе№іж–№гҒ—гҒҰ +1 гҒ«гҒӘгӮӢ p еҖӢгҒ®гғҷгӮҜгғҲгғ«гҒЁе№іж–№гҒ—гҒҰ вҲ’1 гҒ«гҒӘгӮӢ q еҖӢгҒ®гғҷгӮҜгғҲгғ«гӮ’жҢҒгҒӨгҖӮ Cв„“0,0(R) гҒҜиҮӘ然гҒ« R гҒ«еҗҢеһӢгҒ§гҒӮгӮӢгҒ“гҒЁгҒ«жіЁж„ҸгҒҷгӮӢгҖӮ0 гҒ§гҒӘгҒ„гғҷгӮҜгғҲгғ«гҒҜгҒӘгҒ„гҒӢгӮүгҒ§гҒӮгӮӢгҖӮCв„“0,1(R) гҒҜе№іж–№гҒ—гҒҰ вҲ’1 гҒ«гҒӘгӮӢгҒҹгҒ 1 гҒӨгҒ®гғҷгӮҜгғҲгғ« e1 гҒ«гӮҲгҒЈгҒҰз”ҹжҲҗгҒ•гӮҢгӮӢ 2 ж¬Ўе…ғгҒ®д»Јж•°гҒӘгҒ®гҒ§иӨҮзҙ ж•°дҪ“ C гҒ«еҗҢеһӢгҒ§гҒӮгӮӢгҖӮд»Јж•° Cв„“0,2(R) гҒҜ {1, e1, e2, e1e2} гҒ«гӮҲгҒЈгҒҰејөгӮүгӮҢгӮӢ 4 ж¬Ўе…ғгҒ®д»Јж•°гҒ§гҒӮгӮӢгҖӮеҫҢгӮҚ 3 гҒӨгҒ®е…ғгҒҜе№іж–№гҒ—гҒҰ вҲ’1 гҒ«гҒӘгӮҠгҒҷгҒ№гҒҰеҸҚдәӨжҸӣгҒҷгӮӢгҒ®гҒ§гҖҒд»Јж•°гҒҜеӣӣе…ғж•°дҪ“ H гҒ«еҗҢеһӢгҒ§гҒӮгӮӢгҖӮCв„“0,3(R) гҒҜ еҲҶи§ЈеһӢеҸҢеӣӣе…ғж•°гҒЁе‘јгҒ°гӮҢгӮӢзӣҙе’Ң H вҠ• H гҒ«еҗҢеһӢгҒӘ 8 ж¬Ўе…ғгҒ®д»Јж•°гҒ§гҒӮгӮӢгҖӮ иӨҮзҙ дҝӮж•°гҒ®е ҙеҗҲиӨҮзҙ гғҷгӮҜгғҲгғ«з©әй–“дёҠгҒ§гӮӮгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гӮ’иҖғгҒҲгӮӢгҒ“гҒЁгҒҢгҒ§гҒҚгӮӢгҖӮиӨҮзҙ гғҷгӮҜгғҲгғ«з©әй–“дёҠгҒ®гҒҷгҒ№гҒҰгҒ®йқһйҖҖеҢ–дәҢж¬ЎеҪўејҸгҒҜжЁҷжә–еҜҫи§’еҪўејҸ гҒҹгҒ гҒ— n = dim VгҖҒгҒ«еҗҢеһӢгӮ’йҷӨгҒ„гҒҰеҗҢеҖӨгҒ§гҒӮгӮҠгҖҒгҒ—гҒҹгҒҢгҒЈгҒҰеҗ„ж¬Ўе…ғ n гҒ«еҜҫгҒ—гҒҰгҒҹгҒ 1гҒӨгҒ®йқһйҖҖеҢ–гҒӘгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒҢеӯҳеңЁгҒҷгӮӢгҖӮжЁҷжә–дәҢж¬ЎеҪўејҸгӮ’жҢҒгҒЈгҒҹ Cn дёҠгҒ®гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гӮ’ Cв„“n(C) гҒЁиЎЁиЁҳгҒ—гӮҲгҒҶгҖӮ жңҖеҲқгҒ®гҒ„гҒҸгҒӨгҒӢгҒ®е ҙеҗҲгҒ®иЁҲз®—гҒҜйӣЈгҒ—гҒҸгҒҜгҒӘгҒҸгҒҰ
гҒ§гҒӮгӮӢгҒ“гҒЁгҒҢгӮҸгҒӢгӮӢгҖҒгҒҹгҒ гҒ— M(n, C) гҒҜ C дёҠ nГ—n иЎҢеҲ—гҒ®д»Јж•°гӮ’иЎЁгҒҷгҖӮ дҫӢпјҡеӣӣе…ғж•°гҒЁеҸҢеҜҫеӣӣе…ғж•°гҒ®ж§ӢжҲҗеӣӣе…ғж•°гҒ“гҒ®гӮ»гӮҜгӮ·гғ§гғігҒ«гҒҠгҒ„гҒҰгҖҒгғҸгғҹгғ«гғҲгғігҒ®еӣӣе…ғж•°гҒҢгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•° Cв„“0,3(R) гҒ®еҒ¶йғЁеҲҶд»Јж•°гҒЁгҒ—гҒҰж§ӢжҲҗгҒ•гӮҢгӮӢгҖӮ гғҷгӮҜгғҲгғ«з©әй–“ V гӮ’е®ҹ 3 ж¬Ўе…ғз©әй–“ R3 гҒЁгҒ—гҖҒдәҢж¬ЎеҪўејҸ Q гӮ’йҖҡеёёгҒ®гғҰгғјгӮҜгғӘгғғгғүиЁҲйҮҸгҒӢгӮүе…ҘгӮҢгӮӢгҖӮгҒҷгӮӢгҒЁгҖҒдәҢж¬ЎеҪўејҸгҒӮгӮӢгҒ„гҒҜгӮ№гӮ«гғ©гғјз©ҚгҒҜ v, w вҲҲ R3 гҒ«еҜҫгҒ—гҒҰ гҒЁгҒӘгӮӢгҖӮгҒ„гҒҫж¬ЎејҸгҒ§дёҺгҒҲгӮүгӮҢгӮӢгғҷгӮҜгғҲгғ« v гҒЁ w гҒ®гӮҜгғӘгғ•гӮ©гғјгғүз©ҚгӮ’е°Һе…ҘгҒҷгӮӢ гҒ“гҒ®е®ҡејҸеҢ–гҒҜиІ гҒ®з¬ҰеҸ·гӮ’з”ЁгҒ„гӮӢгҒ“гҒЁгҒ§еӣӣе…ғж•°гҒЁгҒ®еҜҫеҝңгӮ’зӨәгҒҷгҒ“гҒЁгӮ’е®№жҳ“гҒ«гҒ—гҒҰгҒ„гӮӢгҖӮ R3 гҒ®зӣҙдәӨеҚҳдҪҚгғҷгӮҜгғҲгғ«гҒ®йӣҶеҗҲгӮ’ e1, e2, e3 гҒЁгҒ—гҒҰиЎЁиЁҳгҒҷгӮӢгҒЁгҖҒгӮҜгғӘгғ•гӮ©гғјгғүз©ҚгҒҜй–ўдҝӮ гҒҠгӮҲгҒі гӮ’з”ҹгҒҝеҮәгҒҷгҖӮгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•° Cв„“0,3(R) гҒ®дёҖиҲ¬гҒ®е…ғгҒҜ гҒ«гӮҲгҒЈгҒҰдёҺгҒҲгӮүгӮҢгӮӢгҖӮ Cв„“0,3(R) гҒ®еҒ¶ж¬Ўж•°е…ғгҒ®з·ҡеһӢзөҗеҗҲгҒҜдёҖиҲ¬е…ғ гҒЁгҒЁгӮӮгҒ« Cв„“ 0 гҒЁгҒ—гҒҰеҗҢдёҖиҰ–гҒҷгӮӢгҒ“гҒЁгҒҢгҒ§гҒҚгҖҒгҒ“гӮҢгҒҜеҒ¶йғЁеҲҶд»Јж•° Cв„“ 0 гҒ“гӮҢгӮ’иҰӢгӮӢгҒ«гҒҜгҖҒ гҒЁ гӮ’иЁҲз®—гҒҷгӮӢгҖӮжңҖеҫҢгҒ«гҖҒ еҸҢеҜҫеӣӣе…ғж•°гҒ“гҒ®гӮ»гӮҜгӮ·гғ§гғігҒ«гҒҠгҒ„гҒҰгҖҒеҸҢеҜҫеӣӣе…ғж•°гҒҢйҖҖеҢ–дәҢж¬ЎеҪўејҸгӮ’жҢҒгҒЈгҒҹе®ҹеӣӣж¬Ўе…ғз©әй–“гҒ®еҒ¶гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒЁгҒ—гҒҰж§ӢжҲҗгҒ•гӮҢгӮӢ[5][6]гҖӮ гғҷгӮҜгғҲгғ«з©әй–“ V гӮ’е®ҹеӣӣж¬Ўе…ғз©әй–“ R4 гҒЁгҒ—гҖҒдәҢж¬ЎеҪўејҸ Q гӮ’ R3 дёҠгҒ®гғҰгғјгӮҜгғӘгғғгғүи·қйӣўгҒӢгӮүе…ҘгӮӢйҖҖеҢ–еҪўејҸгҒЁгҒҷгӮӢгҖӮv, w вҲҲ R4 гҒ«еҜҫгҒ—гҒҰгҖҒйҖҖеҢ–еҸҢз·ҡеһӢеҪўејҸ гӮ’е°Һе…ҘгҒҷгӮӢгҖӮгҒ“гҒ®йҖҖеҢ–гӮ№гӮ«гғ©гғјз©ҚгҒҜ R4 гҒ«гҒҠгҒ‘гӮӢи·қйӣўжё¬е®ҡгӮ’ R3 гҒ®и¶…е№ійқўгҒ«е…Ёе°„гҒ§е°„еҪұгҒҷгӮӢгҖӮ гғҷгӮҜгғҲгғ« v гҒЁ w гҒ®гӮҜгғӘгғ•гӮ©гғјгғүз©ҚгҒҜ гҒ«гӮҲгҒЈгҒҰдёҺгҒҲгӮүгӮҢгӮӢгҖӮиІ еҸ·гҒҜеӣӣе…ғж•°гҒЁгҒ®еҜҫеҝңгӮ’з°ЎеҚҳгҒ«гҒҷгӮӢгҒҹгӮҒгҒ«е°Һе…ҘгҒ—гҒҰгҒ„гӮӢгҒ“гҒЁгҒ«жіЁж„ҸгҒ—гӮҲгҒҶгҖӮ R4 гҒ®зӣҙдәӨеҚҳдҪҚгғҷгӮҜгғҲгғ«гҒ®йӣҶеҗҲгӮ’ e1, e2, e3, e4 гҒЁгҒ—гҒҰиЎЁиЁҳгҒҷгӮӢгҒЁгҖҒгӮҜгғӘгғ•гӮ©гғјгғүз©ҚгҒҜй–ўдҝӮ гҒЁ гӮ’з”ҹгҒҝеҮәгҒҷгҖӮ гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•° Cв„“(R4,d) гҒ®дёҖиҲ¬е…ғгҒҜ 16 еҖӢгҒ®жҲҗеҲҶгӮ’жҢҒгҒӨгҖӮеҒ¶ж¬Ўж•°д»ҳгҒ‘гӮүгӮҢгҒҹе…ғгҒ®з·ҡеһӢзөҗеҗҲгҒҜж¬ЎгҒ®еҪўгҒ®дёҖиҲ¬е…ғгӮ’жҢҒгҒЈгҒҹеҒ¶йғЁеҲҶд»Јж•° Cв„“0(R4,d) гӮ’е®ҡзҫ©гҒҷгӮӢ еҹәеә•е…ғгҒҜеӣӣе…ғж•°еҹәеә•е…ғ i, j, k гҒЁеҸҢеҜҫеҚҳдҪҚ Оө гҒЁ гҒЁгҒ—гҒҰеҗҢдёҖиҰ–гҒ§гҒҚгӮӢгҖӮгҒ“гӮҢгҒҜ Cв„“ 0 гҒ“гӮҢгӮ’иҰӢгӮӢгҒ«гҒҜгҖҒж¬ЎејҸгӮ’иЁҲз®—гҒҷгӮӢ гҒЁ e1 гҒЁ e4 гҒ®дәӨжҸӣгҒҜеҒ¶ж•°еӣһз¬ҰеҸ·гӮ’дәӨд»ЈгҒ—гҖҒеҸҢеҜҫеҚҳдҪҚ Оө гҒҢеӣӣе…ғж•°еҹәеә•е…ғ i, j, k гҒЁдәӨжҸӣгҒҷгӮӢгҒ“гҒЁгӮ’зӨәгҒҷгҖӮ жҖ§иіӘеӨ–з©Қд»Јж•°гҒЁгҒ®й–ўдҝӮгғҷгӮҜгғҲгғ«з©әй–“ V гҒҢдёҺгҒҲгӮүгӮҢгӮӢгҒЁеӨ–з©Қд»Јж•° вӢҖ(V) гӮ’ж§ӢжҲҗгҒ§гҒҚгҖҒгҒқгҒ®ж¬Ўе…ғгҒҜ V дёҠгҒ®гҒ©гӮ“гҒӘдәҢж¬ЎеҪўејҸгҒӢгӮүгӮӮзӢ¬з«ӢгҒ§гҒӮгӮӢгҖӮK гҒҢжЁҷж•° 2 гҒ§гҒӘгҒ‘гӮҢгҒ° вӢҖ(V) гҒЁ Cв„“(V, Q) гҒ®й–“гҒ«гғҷгӮҜгғҲгғ«з©әй–“гҒЁгҒ—гҒҰиҖғгҒҲгҒҰиҮӘ然гҒӘеҗҢеһӢгҒҢеӯҳеңЁгҒҷгӮӢпјҲгҒқгҒ—гҒҰжЁҷж•°гҒҢ 2 гҒ§гҒӘгҒ„е ҙеҗҲгҒ«гҒҜиҮӘ然гҒ§гҒӘгҒ„гҒӢгӮӮгҒ—гӮҢгҒӘгҒ„еҗҢеһӢгҒҢеӯҳеңЁгҒҷгӮӢпјүгҒЁгҒ„гҒҶгҒ“гҒЁгҒҢеҲӨжҳҺгҒҷгӮӢгҖӮгҒ“гӮҢгҒҢд»Јж•°еҗҢеһӢгҒ§гҒӮгӮӢгҒ“гҒЁгҒЁ Q = 0 гҒҜеҗҢеҖӨгҒ§гҒӮгӮӢгҖӮгҒ—гҒҹгҒҢгҒЈгҒҰгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•° Cв„“(V, Q) гӮ’ Q гҒ«дҫқеӯҳгҒ—гҒҹз©ҚгҒ§ V дёҠгҒ®еӨ–з©Қд»Јж•°гӮ’иұҠгҒӢгҒ«гҒ—гҒҹгӮӮгҒ®пјҲгҒӮгӮӢгҒ„гҒҜгӮҲгӮҠжӯЈзўәгҒ«гҒҜгҖҒйҮҸеӯҗеҢ–гҖҒ cf. е°Һе…ҘпјүгҒЁиҖғгҒҲгӮӢгҒ“гҒЁгҒҢгҒ§гҒҚгӮӢпјҲеӨ–з©ҚгҒҜгҒӘгҒҠ Q гҒЁгҒҜзӢ¬з«ӢгҒ«е®ҡзҫ©гҒ§гҒҚгӮӢпјүгҖӮ еҗҢеһӢгӮ’зўәз«ӢгҒҷгӮӢжңҖгӮӮжҳ“гҒ—гҒ„ж–№жі•гҒҜ V гҒ®зӣҙдәӨеҹәеә• {ei} гӮ’гҒЁгӮҠгҒқгӮҢгӮ’дёҠгҒ§иҝ°гҒ№гӮүгӮҢгҒҹгӮҲгҒҶгҒ« Cв„“(V, Q) гҒ®еҹәеә•гҒ«жӢЎејөгҒҷгӮӢгҒ“гҒЁгҒ§гҒӮгӮӢгҖӮеҶҷеғҸ Cв„“(V, Q) вҶ’ вӢҖ(V) гҒҜ гҒ«гӮҲгҒЈгҒҰжұәе®ҡгҒ•гӮҢгӮӢгҖӮгҒ“гӮҢгҒҜеҹәеә• {ei} гҒҢзӣҙдәӨгҒ—гҒҰгҒ„гӮӢгҒЁгҒҚгҒ«гҒ®гҒҝгҒҶгҒҫгҒҸгҒ„гҒҸгҒ“гҒЁгҒ«жіЁж„ҸгҒ—гӮҲгҒҶгҖӮгҒ“гҒ®еҶҷеғҸгҒҜзӣҙдәӨеҹәеә•гҒ®йҒёжҠһгҒЁгҒҜзӢ¬з«ӢгҒ§гҒӮгӮҠеҫ“гҒЈгҒҰиҮӘ然еҗҢеһӢгӮ’дёҺгҒҲгӮӢгҒ“гҒЁгӮ’зӨәгҒҷгҒ“гҒЁгҒҢгҒ§гҒҚгӮӢгҖӮ K гҒ®жЁҷж•°гҒҢ 0 гҒ§гҒӮгӮҢгҒ°гҖҒеҸҚеҜҫз§°еҢ–гҒ«гӮҲгҒЈгҒҰгӮӮеҗҢеһӢгӮ’зўәз«ӢгҒ§гҒҚгӮӢгҖӮй–ўж•° fk: V Г— вӢҜ Г— V вҶ’ Cв„“(V, Q) гӮ’ гҒ«гӮҲгҒЈгҒҰе®ҡзҫ©гҒҷгӮӢгҖҒгҒҹгҒ гҒ—е’ҢгҒҜ k еҖӢгҒ®е…ғгҒ®дёҠгҒ®зҪ®жҸӣзҫӨгӮ’жёЎгҒЈгҒҰеҸ–гӮүгӮҢгӮӢгҖӮfk гҒҜдәӨд»ЈеҪўејҸгҒӘгҒ®гҒ§гҒқгӮҢгҒҜдёҖж„Ҹзҡ„гҒӘз·ҡеһӢеҶҷеғҸ вӢҖk(V) вҶ’ Cв„“(V, Q) гӮ’иӘҳе°ҺгҒҷгӮӢгҖӮгҒ“гӮҢгӮүгҒ®еҶҷеғҸгҒ®зӣҙе’ҢгҒҜ вӢҖ(V) гҒЁ Cв„“(V, Q) гҒ®й–“гҒ®з·ҡеһӢеҶҷеғҸгӮ’дёҺгҒҲгӮӢгҖӮгҒ“гҒ®еҶҷеғҸгҒҜз·ҡеһӢеҗҢеһӢгҒ§гҒӮгӮӢгҒ“гҒЁгӮ’зӨәгҒҷгҒ“гҒЁгҒҢгҒ§гҒҚгҖҒгҒқгӮҢгҒҜиҮӘ然гҒ§гҒӮгӮӢгҖӮ й–ўдҝӮгӮ’иҰӢгӮӢгӮҲгӮҠжҙ—з·ҙгҒ•гӮҢгҒҹж–№жі•гҒҜ Cв„“(V, Q) дёҠгғ•гӮЈгғ«гғҲгғ¬гғјгӮ·гғ§гғігӮ’ж§ӢжҲҗгҒҷгӮӢгҒ“гҒЁгҒ§гҒӮгӮӢгҖӮгғҶгғігӮҪгғ«д»Јж•° T(V) гҒҜиҮӘ然гҒӘгғ•гӮЈгғ«гғҲгғ¬гғјгӮ·гғ§гғігӮ’жҢҒгҒӨгҒ“гҒЁгӮ’жҖқгҒ„еҮәгҒқгҒҶпјҡ F0 вҠӮ F1 вҠӮ F2 вҠӮ вӢҜгҖҒгҒҹгҒ гҒ— Fk гҒҜ k-йҡҺд»ҘдёӢгҒ®гғҶгғігӮҪгғ«гҒ®е’ҢгӮ’еҗ«гӮҖгҖӮгҒ“гӮҢгӮ’гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ«е°„еҪұгҒҷгӮӢгҒ“гҒЁгҒ§ Cв„“(V, Q) дёҠгҒ®гғ•гӮЈгғ«гғҲгғ¬гғјгӮ·гғ§гғігҒҢеҫ—гӮүгӮҢгӮӢгҖӮдјҙгҒҶж¬Ўж•°д»Јж•° гҒҜиҮӘ然гҒ«еӨ–з©Қд»Јж•° вӢҖ(V) гҒ«еҗҢеһӢгҒ§гҒӮгӮӢгҖӮгғ•гӮЈгғ«гӮҝгғјд»Јж•°гҒ®дјҙгҒҶж¬Ўж•°д»Јж•°гҒҜпјҲгҒҷгҒ№гҒҰгҒ® k гҒ«еҜҫгҒ—гҒҰFk гҒ®гӮігғігғқгғјгғҚгғігғҲгӮ’ Fk+1 гҒ®дёӯгҒ«йҒёгҒ¶гҒ“гҒЁгҒ«гӮҲгҒЈгҒҰпјүгҒӨгҒӯгҒ«гғ•гӮЈгғ«гӮҝгғјгғҷгӮҜгғҲгғ«з©әй–“гҒЁгҒ—гҒҰгғ•гӮЈгғ«гӮҝгғјд»Јж•°гҒ«еҗҢеһӢгҒ§гҒӮгӮӢгҒӢгӮүгҖҒгҒ“гӮҢгҒҜд»»ж„ҸгҒ®жЁҷж•°гҒ«гҒҠгҒ„гҒҰгҖҒ2 гҒ§гҒ•гҒҲгӮӮгҖҒпјҲиҮӘ然гҒӘгӮӮгҒ®гҒ§гҒҜгҒӘгҒ„гҒҢпјүеҗҢеһӢгӮ’жҸҗдҫӣгҒҷгӮӢгҖӮ ж¬Ўж•°д»ҳгҒ‘д»ҘйҷҚгҒ§гҒҜжЁҷж•°гҒҜ 2 гҒ§гҒӘгҒ„гҒЁгҒҷгӮӢ[жіЁйҮҲ 2]гҖӮ гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒҜ Z2-ж¬Ўж•°д»Јж•°пјҲи¶…д»Јж•°гҒЁгҒ—гҒҰгӮӮзҹҘгӮүгӮҢгҒҰгҒ„гӮӢпјүгҒ§гҒӮгӮӢгҖӮе®ҹйҡӣгҖҒv вҶҰ вҲ’v гҒ«гӮҲгҒЈгҒҰе®ҡзҫ©гҒ•гӮҢгӮӢ V дёҠгҒ®з·ҡеһӢеҶҷеғҸпјҲеҺҹзӮ№гӮ’йҖҡгӮӢеҸҚе°„пјүгҒҜдәҢж¬ЎеҪўејҸ Q гӮ’дҝқеӯҳгҒ—гҒ—гҒҹгҒҢгҒЈгҒҰгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®жҷ®йҒҚжҖ§гҒ«гӮҲгҒЈгҒҰд»Јж•°иҮӘе·ұеҗҢеһӢ
гҒ«жӢЎејөгҒҷгӮӢгҖӮОұ гҒҜеҜҫеҗҲпјҲгҒҷгҒӘгӮҸгҒЎиҮӘд№—гҒҷгӮӢгҒЁжҒ’зӯүй–ўж•°гҒ«гҒӘгӮӢпјүгҒ§гҒӮгӮӢгҒӢгӮүгҖҒCв„“(V, Q) гӮ’ Оұ гҒ®жӯЈгҒЁиІ гҒ®еӣәжңүз©әй–“гҒ«еҲҶи§ЈгҒ§гҒҚгӮӢ гҒҹгҒ гҒ— Cв„“i(V, Q) вү” {x вҲҲ Cв„“(V, Q) вҒҹ|вҒҹ Оұ(x) = (вҲ’1)ix}гҖӮОұ гҒҜиҮӘе·ұеҗҢеһӢгҒ§гҒӮгӮӢгҒӢгӮү гҒҢеҫ“гҒҶгҖҒгҒҹгҒ гҒ—еҸідёҠгҒ®ж·»гҒҲеӯ—гҒҜ modulo 2 гҒ§иӘӯгҒҫгӮҢгӮӢгҖӮгҒ“гӮҢгҒҜ Cв„“(V, Q) гҒ« Z2-ж¬Ўж•°д»Јж•°гҒ®ж§ӢйҖ гӮ’дёҺгҒҲгӮӢгҖӮйғЁеҲҶз©әй–“ Cв„“0(V, Q) гҒҜ Cв„“(V, Q) гҒ®йғЁеҲҶд»Јж•°гӮ’гҒӘгҒ—гҖҒеҒ¶йғЁеҲҶд»Јж•° (even subalgebra) гҒЁе‘јгҒ°гӮҢгӮӢгҖӮйғЁеҲҶз©әй–“ Cв„“1(V, Q) гҒҜ Cв„“(V, Q) гҒ®еҘҮжҲҗеҲҶ (odd part) гҒЁе‘јгҒ°гӮҢгӮӢпјҲйғЁеҲҶд»Јж•°гҒ§гҒҜгҒӘгҒ„пјүгҖӮгҒ“гҒ® Z2-ж¬Ўж•°д»ҳгҒ‘гҒҜгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®и§ЈжһҗгҒЁеҝңз”ЁгҒ«гҒҠгҒ„гҒҰйҮҚиҰҒгҒӘеҪ№еүІгӮ’жһңгҒҹгҒҷгҖӮиҮӘе·ұеҗҢеһӢ Оұ гҒҜдё»еҜҫеҗҲ (main involution) гҒӮгӮӢгҒ„гҒҜж¬Ўж•°д»ҳгҒҚеҜҫеҗҲ (grade involution) гҒЁе‘јгҒ°гӮҢгӮӢгҖӮгҒ“гҒ® Z2-ж¬Ўж•°д»ҳгҒ‘гҒ«гҒҠгҒ„гҒҰ pure гҒӘе…ғгҒҜеҚҳгҒ« even гҒӮгӮӢгҒ„гҒҜ odd гҒЁе‘јгҒ°гӮҢгӮӢгҖӮ
гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®еҒ¶йғЁеҲҶд»Јж•° Cв„“0(V, Q) гҒҜгҒқгӮҢгҒӮгӮӢиҮӘиә«гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ«еҗҢеһӢгҒ§гҒӮгӮӢ[жіЁйҮҲ 4][жіЁйҮҲ 5]V гҒҢгғҺгғ«гғ Q(a) гҒ®йғЁеҲҶз©әй–“ U гҒ®гғҷгӮҜгғҲгғ« a гҒ®зӣҙдәӨзӣҙе’ҢгҒ§гҒӮгӮҢгҒ°гҖҒCв„“0(V, Q) гҒҜ Cв„“(U, вҲ’Q(a)Q) гҒ«еҗҢеһӢгҒ§гҒӮгӮӢгҖҒгҒҹгҒ гҒ— вҲ’Q(a)Q гҒҜ U гҒ«еҲ¶йҷҗгҒ•гӮҢ вҲ’Q(a) гӮ’жҺӣгҒ‘гҒҹеҪўејҸ Q гҒ§гҒӮгӮӢгҖӮзү№гҒ«е®ҹж•°дҪ“дёҠгҒ“гӮҢгҒҜж¬ЎгӮ’ж„Ҹе‘ігҒҷгӮӢ иІ е®ҡеҖӨгҒ®е ҙеҗҲгҒ«гҒҜгҒ“гӮҢгҒҜеҢ…еҗ« Cв„“0,nвҲ’1(R) вҠӮ Cв„“0,n(R) гӮ’дёҺгҒҲгҖҒеҲ—гӮ’жӢЎејөгҒҷгӮӢ
еҗҢж§ҳгҒ«гҖҒиӨҮзҙ гҒ®е ҙеҗҲгҒ«гҒҜгҖҒCв„“n(C) гҒ®еҒ¶йғЁеҲҶд»Јж•°гҒҜ Cв„“nвҲ’1(C) гҒ«еҗҢеһӢгҒ§гҒӮгӮӢгҒ“гҒЁгӮ’зӨәгҒӣгӮӢгҖӮ еҸҚиҮӘе·ұеҗҢеһӢеҶҷеғҸиҮӘе·ұеҗҢеһӢ Оұ гҒ«еҠ гҒҲгҒҰгҖҒгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®и§ЈжһҗгҒ«гҒҠгҒ„гҒҰйҮҚиҰҒгҒӘеҪ№еүІгӮ’жһңгҒҹгҒҷ 2 гҒӨгҒ®еҸҚиҮӘе·ұеҗҢеһӢгҒҢеӯҳеңЁгҒҷгӮӢгҖӮгғҶгғігӮҪгғ«д»Јж•° T(V) гҒҜгҒҷгҒ№гҒҰгҒ®з©ҚгҒ®й ҶеәҸгӮ’йҖҶгҒ«гҒҷгӮӢеҸҚиҮӘе·ұеҗҢеһӢгҒЁгҒЁгӮӮгҒ«жқҘгӮӢгҒ“гҒЁгӮ’жҖқгҒ„еҮәгҒқгҒҶпјҡ гӮӨгғҮгӮўгғ« IQ гҒҜгҒ“гҒ®еҸҚи»ўгҒ®дёӢгҒ§дёҚеӨүгҒӘгҒ®гҒ§гҖҒгҒ“гҒ®жј”з®—гҒҜ Cв„“(V, Q) гҒ®еҸҚиҮӘе·ұеҗҢеһӢгҒ«йҷҚгӮҠгҖҒи»ўзҪ® (transpose) гҒӮгӮӢгҒ„гҒҜеҸҚи»ў (reversal) жј”з®—гҒЁе‘јгҒ°гӮҢгҖҒtx гҒ«гӮҲгҒЈгҒҰиЎЁиЁҳгҒ•гӮҢгӮӢгҖӮгҒ“гҒ®еҸҚи»ўгҒҜеҸҚиҮӘе·ұеҗҢеһӢгҒ§гҒӮгӮӢпјҡ t(xy) = ty txгҖӮи»ўзҪ®жј”з®—гҒҜ Z2-ж¬Ўж•°д»ҳгҒ‘гӮ’е…ЁгҒҸдҪҝгӮҸгҒӘгҒ„гҒ®гҒ§2гҒӨзӣ®гҒ®еҸҚиҮӘе·ұеҗҢеһӢгӮ’ Оұ гҒЁи»ўзҪ®гӮ’еҗҲжҲҗгҒҷгӮӢгҒ“гҒЁгҒ«гӮҲгҒЈгҒҰе®ҡзҫ©гҒҷгӮӢгҖӮгҒ“гҒ®жј”з®—гӮ’гӮҜгғӘгғ•гӮ©гғјгғүе…ұеҪ№ (Clifford conjugation) гҒЁе‘јгҒі x гҒЁиЎЁиЁҳгҒҷгӮӢ 2 гҒӨгҒ®еҸҚиҮӘе·ұеҗҢеһӢгҒ®гҒҶгҒЎи»ўзҪ®гҒҜгӮҲгӮҠеҹәжң¬зҡ„гҒ§гҒӮгӮӢ[жіЁйҮҲ 6]гҖӮ гҒ“гӮҢгӮүгҒ®жј”з®—гҒҜе…ЁгҒҰеҜҫеҗҲгҒ§гҒӮгӮӢгҒ“гҒЁгҒ«жіЁж„ҸгҒ—гӮҲгҒҶгҖӮгҒқгӮҢгӮүгҒҜ Z-ж¬Ўж•°д»ҳгҒ‘гҒ«гҒҠгҒ„гҒҰ pure гҒӘе…ғдёҠ Вұ1 гҒЁгҒ—гҒҰдҪңз”ЁгҒҷгӮӢгҒ“гҒЁгӮ’зӨәгҒҷгҒ“гҒЁгҒҢгҒ§гҒҚгӮӢгҖӮе®ҹйҡӣгҖҒгҒҷгҒ№гҒҰгҒ® 3 гҒӨгҒ®жј”з®—гҒҜж¬Ўж•° modulo 4 гҒ«гҒ—гҒӢдҫқгӮүгҒӘгҒ„гҖӮгҒӨгҒҫгӮҠгҖҒx гҒҢ pure гҒ§ж¬Ўж•° k гҒ§гҒӮгӮҢгҒ°гҖҒ гҒҹгҒ гҒ—з¬ҰеҸ·гҒҜд»ҘдёӢгҒ®иЎЁгҒ«гӮҲгҒЈгҒҰдёҺгҒҲгӮүгӮҢгӮӢпјҡ
гӮҜгғӘгғ•гӮ©гғјгғүгӮ№гӮ«гғ©гғјз©ҚжЁҷж•°гҒҢ 2 гҒ§гҒӘгҒ„гҒЁгҒҚгҖҒV дёҠгҒ®дәҢж¬ЎеҪўејҸ Q гҒҜ Cв„“(V, Q) гҒ®гҒҷгҒ№гҒҰгҒ®дёҠгҒ®дәҢж¬ЎеҪўејҸгҒ«жӢЎејөгҒҷгӮӢгҒ“гҒЁгҒҢгҒ§гҒҚгӮӢпјҲгҒ“гӮҢгӮӮ Q гҒ«гӮҲгҒЈгҒҰиЎЁиЁҳгҒҷгӮӢпјүгҖӮ1 гҒӨгҒ®гҒқгҒ®гӮҲгҒҶгҒӘжӢЎејөгҒ®еҹәеә•гҒ«дҫқеӯҳгҒ—гҒӘгҒ„е®ҡзҫ©гҒҜ гҒҹгҒ гҒ— гҒҜ a гҒ®гӮ№гӮ«гғ©гғјйғЁеҲҶпјҲZ-ж¬Ўж•°д»ҳгҒ‘гҒ«гҒҠгҒ„гҒҰж¬Ўж•° 0 гҒ®йғЁеҲҶпјүгӮ’иЎЁиЁҳгҒҷгӮӢгҖӮ гӮ’зӨәгҒҷгҒ“гҒЁгҒҢгҒ§гҒҚгӮӢгҖҒгҒҹгҒ гҒ— vi гҒҜ V гҒ®е…ғгҒ§гҒӮгӮӢ вҖ“ гҒ“гҒ®жҒ’зӯүејҸгҒҜ Cв„“(V, Q) гҒ®д»»ж„ҸгҒ®е…ғгҒ«еҜҫгҒ—гҒҰгҒҜжӯЈгҒ—гҒҸгҖҢгҒӘгҒ„гҖҚгҖӮ Cв„“(V, Q) дёҠгҒ®дјҙгҒҶеҜҫз§°еҸҢз·ҡеһӢеҪўејҸгҒҜ гҒ«гӮҲгҒЈгҒҰдёҺгҒҲгӮүгӮҢгӮӢгҖӮгҒ“гӮҢгҒҜ V гҒ«еҲ¶йҷҗгҒ•гӮҢгҒҹгҒЁгҒҚгҒ«гӮӮгҒЁгҒ®еҸҢз·ҡеһӢеҪўејҸгҒ«жҲ»гӮӢгҒ“гҒЁгӮ’зўәиӘҚгҒ§гҒҚгӮӢгҖӮ Cв„“(V, Q) гҒ®гҒҷгҒ№гҒҰгҒ®дёҠгҒ®еҸҢз·ҡеһӢеҪўејҸгҒҢйқһйҖҖеҢ–гҒ§гҒӮгӮӢгҒ“гҒЁгҒЁгҒқгӮҢгҒҢ V дёҠйқһйҖҖеҢ–гҒ§гҒӮгӮӢгҒ“гҒЁгҒҜеҗҢеҖӨгҒ§гҒӮгӮӢгҖӮ и»ўзҪ®гҒҜгҒ“гҒ®еҶ…з©ҚгҒ«й–ўгҒ—гҒҰе·Ұ/еҸігӮҜгғӘгғ•гӮ©гғјгғүд№—жі•гҒ®йҡҸдјҙгҒ§гҒӮгӮӢгҒ“гҒЁгӮ’иЁјжҳҺгҒҷгӮӢгҒ®гҒҜйӣЈгҒ—гҒҸгҒӘгҒ„гҖӮгҒӨгҒҫгӮҠгҖҒ гҒҠгӮҲгҒі гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®ж§ӢйҖгҒ“гҒ®зҜҖгҒ§гҒҜгғҷгӮҜгғҲгғ«з©әй–“ V гҒ®ж¬Ўе…ғгҒҜжңүйҷҗгҒ§гҒӮгӮҠ Q гҒ®еҸҢз·ҡеһӢеҪўејҸгҒҜйқһзү№з•°гҒ§гҒӮгӮӢгҒЁд»®е®ҡгҒҷгӮӢгҖӮK дёҠгҒ®дёӯеҝғеҚҳзҙ”д»Јж•°гҒҜдёӯеҝғгҒҢ K гҒ®пјҲжңүйҷҗж¬Ўе…ғпјүеҸҜйҷӨд»Јж•°дёҠгҒ®иЎҢеҲ—д»Јж•°гҒ§гҒӮгӮӢгҖӮдҫӢгҒҲгҒ°гҖҒе®ҹж•°дҪ“дёҠгҒ®дёӯеҝғеҚҳзҙ”д»Јж•°гҒҜе®ҹж•°дҪ“гҒӮгӮӢгҒ„гҒҜеӣӣе…ғж•°дҪ“дёҠгҒ®иЎҢеҲ—д»Јж•°гҒ§гҒӮгӮӢгҖӮ
д»ҘдёӢгҒ®зөҗжһңгӮ’з”ЁгҒ„гӮӢгҒЁгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®ж§ӢйҖ гҒҜжҳҺзӨәзҡ„гҒ«и§ЈжҳҺгҒ•гӮҢгӮӢгҖӮU гҒ®ж¬Ўе…ғгҒҜеҒ¶ж•°гҒ§еҲӨеҲҘејҸ d гҒ®йқһзү№з•°еҸҢз·ҡеһӢеҪўејҸгӮ’жҢҒгҒЈгҒҰгҒ„гӮӢгҒЁгҒ—гҖҒV гҒҜдәҢж¬ЎеҪўејҸгӮ’жҢҒгҒӨеҲҘгҒ®з©әй–“гҒЁгҒҷгӮӢгҖӮU + V гҒ®гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒҜ U гҒЁ (вҲ’1)dim(U)/2dV гҒ®гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®гғҶгғігӮҪгғ«з©ҚгҒ«еҗҢеһӢгҒ§гҒӮгӮҠгҖҒеҫҢиҖ…гҒҜгҒқгҒ®дәҢж¬ЎеҪўејҸгҒ« (вҲ’1)dim(U)/2d гӮ’жҺӣгҒ‘гҒҹз©әй–“ V гҒ§гҒӮгӮӢгҖӮгҒ“гӮҢгҒҜе®ҹж•°дҪ“дёҠгҒ§гҒҜзү№гҒ«ж¬ЎгҒ®гҒ“гҒЁгӮ’ж„Ҹе‘ігҒҷгӮӢ гҒ“гӮҢгӮүгҒ®е…¬ејҸгӮ’з”ЁгҒ„гӮӢгҒ“гҒЁгҒ§е®ҹгҒЁиӨҮзҙ гҒ®гҒҷгҒ№гҒҰгҒ®гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®ж§ӢйҖ гҒҢе°ҺгҒӢгӮҢгӮӢгҖӮгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®еҲҶйЎһгӮ’иҰӢгӮҲгҖӮ гҒЁгӮҠгӮҸгҒ‘гҖҒгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®жЈ®з”°еҗҢеҖӨйЎһпјҲгҒқгҒ®иЎЁзҸҫи«–пјҡ гҒқгӮҢдёҠгҒ®еҠ зҫӨгҒ®еңҸгҒ®еҗҢеҖӨйЎһпјүгҒҜз¬ҰеҸ· (p вҲ’ q) mod 8 гҒ®гҒҝгҒ«дҫқгҒЈгҒҰгҒ„гӮӢгҖӮгҒ“гӮҢгҒҜгғңгғғгғҲгҒ®е‘ЁжңҹжҖ§гҒ®д»Јж•°зҡ„гҒӘеҪўгҒ§гҒӮгӮӢгҖӮ гӮҜгғӘгғ•гӮ©гғјгғүзҫӨгӮҜгғӘгғ•гӮ©гғјгғүзҫӨгҒ®гӮҜгғ©гӮ№гҒҜгғ«гғүгғ«гғ•гғ»гғӘгғ—гӮ·гғғгғ„ (Rudolf Lipschitz) гҒ«гӮҲгҒЈгҒҰзҷәиҰӢгҒ•гӮҢгҒҹ[7]гҖӮ гҒ“гҒ®гӮ»гӮҜгӮ·гғ§гғігҒ«гҒҠгҒ„гҒҰ V гҒҜжңүйҷҗж¬Ўе…ғгҒ§дәҢж¬ЎеҪўејҸ Q гҒҜйқһйҖҖеҢ–гҒ§гҒӮгӮӢгҒЁд»®е®ҡгҒҷгӮӢгҖӮ гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®е…ғгҒёгҒ®гҒқгҒ®еҸҜйҖҶе…ғгҒ®зҫӨгҒ«гӮҲгӮӢдҪңз”ЁгҒҜгҒІгҒӯгӮүгӮҢгҒҹе…ұи»ӣ (twisted conjugation) гҒ®иЁҖи‘үгҒ«гӮҲгҒЈгҒҰе®ҡзҫ©гҒ§гҒҚгӮӢгҖӮx гҒҜ y вҶҰ xyОұ(x)вҲ’1 гҒЁеҶҷгҒҷгҖҒгҒҹгҒ гҒ— Оұ гҒҜдёҠгҒ§е®ҡзҫ©гҒ•гӮҢгҒҹ main involutionгҖҒгҒ«гӮҲгӮӢ twisted conjugationгҖӮ гӮҜгғӘгғ•гӮ©гғјгғүзҫӨ О“ гҒҜгҒ“гҒ®дҪңз”ЁгҒ®дёӢгҒ§гғҷгӮҜгғҲгғ«гӮ’е®үе®ҡеҢ–гҒҷгӮӢ (stabilize vectors) еҸҜйҖҶе…ғ x гҒ®йӣҶеҗҲгҒЁгҒ—гҒҰе®ҡзҫ©гҒ•гӮҢгӮӢгҖӮгҒ“гӮҢгҒҢж„Ҹе‘ігҒҷгӮӢгҒ®гҒҜ V гҒ®гҒҷгҒ№гҒҰгҒ® v гҒ«еҜҫгҒ—гҒҰпјҡ гҒ“гҒ®е…¬ејҸгҒҜгҒҫгҒҹгғҺгғ«гғ Q гӮ’дҝқгҒӨгғҷгӮҜгғҲгғ«з©әй–“ V дёҠгҒ®гӮҜгғӘгғ•гӮ©гғјгғүзҫӨгҒ®дҪңз”ЁгӮ’е®ҡзҫ©гҒ—гҖҒеҫ“гҒЈгҒҰгӮҜгғӘгғ•гӮ©гғјгғүзҫӨгҒӢгӮүзӣҙдәӨзҫӨгҒёгҒ®жә–еҗҢеһӢгӮ’дёҺгҒҲгӮӢгҖӮгӮҜгғӘгғ•гӮ©гғјгғүзҫӨгҒҜгғҺгғ«гғ гҒҢ 0 гҒ§гҒӘгҒ„ V гҒ®гҒҷгҒ№гҒҰгҒ®е…ғ r гӮ’еҗ«гҒҝгҖҒгҒ“гӮҢгӮүгҒҜ v гӮ’ v вҲ’ 2вҹЁv,rвҹ©r/Q(r) гҒ«жҢҒгҒЈгҒҰгҒ„гҒҸеҜҫеҝңгҒҷгӮӢйҸЎжҳ гҒ«гӮҲгҒЈгҒҰ V дёҠдҪңз”ЁгҒҷгӮӢгҖӮпјҲжЁҷж•° 2 гҒ«гҒҠгҒ„гҒҰгҒ“гӮҢгӮүгҒҜйҸЎжҳ гҒ§гҒҜгҒӘгҒҸгҖҢзӣҙдәӨ移жҸӣгҖҚ(orthogonal transvection) гҒЁе‘јгҒ°гӮҢгӮӢгҖӮпјү гӮҜгғӘгғ•гӮ©гғјгғүзҫӨ О“ гҒҜ2 гҒӨгҒ®йғЁеҲҶйӣҶеҗҲ О“0 гҒЁ О“1 гҒ®йқһдәӨе’ҢгҒ§гҒӮгӮӢгҖҒгҒҹгҒ гҒ— О“i гҒҜж¬Ўж•° i гҒ®е…ғгҒ®йғЁеҲҶйӣҶеҗҲгҒ§гҒӮгӮӢгҖӮйғЁеҲҶйӣҶеҗҲ О“0 гҒҜ О“ гҒ«гҒҠгҒ„гҒҰжҢҮж•° 2 гҒ®йғЁеҲҶзҫӨгҒ§гҒӮгӮӢгҖӮ V гҒҢжӯЈе®ҡеҖӨпјҲгҒӮгӮӢгҒ„гҒҜиІ е®ҡеҖӨпјүдәҢж¬ЎеҪўејҸгӮ’жҢҒгҒЈгҒҹжңүйҷҗж¬Ўе…ғе®ҹгғҷгӮҜгғҲгғ«з©әй–“гҒ§гҒӮгӮҢгҒ°гӮҜгғӘгғ•гӮ©гғјгғүзҫӨгҒҜпјҲгӮ«гғ«гӮҝгғігғ»гғҮгғҘгғүгғҚгҒ®е®ҡзҗҶгҒ«гӮҲгҒЈгҒҰпјүгҒқгҒ®еҪўејҸгҒ«й–ўгҒ—гҒҰ V гҒ®зӣҙдәӨзҫӨгҒ«е…Ёе°„гҒ—ж ёгҒҜдҪ“ K гҒ® 0 гҒ§гҒӘгҒ„е…ғгҒӢгӮүгҒӘгӮӢгҖӮгҒ“гӮҢгҒҜж¬ЎгҒ®е®Ңе…ЁеҲ—гӮ’е°ҺгҒҸ д»–гҒ®дҪ“дёҠгҒӮгӮӢгҒ„гҒҜдёҚе®ҡеҖӨеҪўејҸгҒ§гҒҜгҖҒеҶҷеғҸгҒҜдёҖиҲ¬гҒ«гҒҜе…Ёе°„гҒ§гҒҜгҒӘгҒҸгҖҒеӨұж•—гҒҜгӮ№гғ”гғҺгғ«гғҺгғ«гғ гҒ«гӮҲгҒЈгҒҰгҒЁгӮүгҒҲгӮүгӮҢгӮӢгҖӮ гӮ№гғ”гғҺгғ«гғҺгғ«гғвҶ’и©ізҙ°гҒҜгҖҢen:Spinor_norm В§ Galois_cohomology_and_orthogonal_groupsгҖҚгӮ’еҸӮз…§
д»»ж„ҸгҒ®жЁҷж•°гҒ«гҒҠгҒ„гҒҰгҖҒгӮ№гғ”гғҺгғ«гғҺгғ«гғ Q гҒҜгӮҜгғӘгғ•гӮ©гғјгғүзҫӨдёҠ гҒ«гӮҲгҒЈгҒҰе®ҡзҫ©гҒ•гӮҢгӮӢгҖӮгҒқгӮҢгҒҜгӮҜгғӘгғ•гӮ©гғјгғүзҫӨгҒӢгӮү K гҒ®йқһйӣ¶е…ғгҒ®зҫӨ K* гҒёгҒ®жә–еҗҢеһӢгҒ§гҒӮгӮӢгҖӮгҒқгӮҢгҒҜ V гӮ’гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®йғЁеҲҶз©әй–“гҒЁеҗҢдёҖиҰ–гҒ—гҒҹгҒЁгҒҚгҒ« V гҒ®дәҢж¬ЎеҪўејҸ Q гҒЁдёҖиҮҙгҒҷгӮӢгҖӮи‘—иҖ…гҒ«гӮҲгҒЈгҒҰгҒҜгӮ№гғ”гғҺгғ«гғҺгғ«гғ гҒ®е®ҡзҫ©гҒҢеғ…гҒӢгҒ«з•°гҒӘгӮҠгҖҒгҒ“гҒ“гҒ§гҒ®гӮӮгҒ®гҒЁгҒҜ О“1 дёҠ вҲ’1, 2, гҒӮгӮӢгҒ„гҒҜ вҲ’2 гҒ®еӣ еӯҗгҒ«гӮҲгҒЈгҒҰз•°гҒӘгӮӢгҖӮйҒ•гҒ„гҒҜжЁҷж•°гҒҢ 2 гҒ§гҒӘгҒ‘гӮҢгҒ°гҒқгӮҢгҒ»гҒ©йҮҚиҰҒгҒ§гҒҜгҒӘгҒ„гҖӮ K гҒ® 0 гҒ§гҒӘгҒ„е…ғгҒҜдҪ“ K гҒ®йқһйӣ¶е…ғгҒ®е№іж–№гҒ®зҫӨ K*2 гҒ«гӮ№гғ”гғҺгғ«гғҺгғ«гғ гӮ’жҢҒгҒӨгҖӮгҒӘгҒ®гҒ§ V гҒҢжңүйҷҗж¬Ўе…ғгҒ§йқһзү№з•°гҒӘгҒЁгҒҚ V гҒ®зӣҙдәӨзҫӨгҒӢгӮүзҫӨ K*/K*2 гҒёгҒ®иӘҳе°ҺеҶҷеғҸгӮ’еҫ—гҖҒгҒ“гӮҢгӮӮгҒҫгҒҹгӮ№гғ”гғҺгғ«гғҺгғ«гғ гҒЁе‘јгҒ°гӮҢгӮӢгҖӮгғҷгӮҜгғҲгғ« r гҒ®йҸЎжҳ гҒ®гӮ№гғ”гғҺгғ«гғҺгғ«гғ гҒҜ K*/K*2 гҒ«гҒҠгҒ„гҒҰеғҸ Q(r) гӮ’жҢҒгҒЎгҖҒгҒ“гҒ®жҖ§иіӘгҒҜзӣҙдәӨзҫӨдёҠгҒқгӮҢгӮ’дёҖж„Ҹзҡ„гҒ«е®ҡзҫ©гҒҷгӮӢгҖӮгҒ“гӮҢгҒҜж¬ЎгҒ®е®Ңе…ЁеҲ—гӮ’дёҺгҒҲгӮӢпјҡ жЁҷж•° 2 гҒ«гҒҠгҒ„гҒҰгҒҜзҫӨ {Вұ1} гҒҜгҒҹгҒ 1 гҒӨгҒ®е…ғгӮ’жҢҒгҒӨгҒ“гҒЁгҒ«жіЁж„ҸгҒӣгӮҲгҖӮ д»Јж•°зҫӨгҒ®гӮ¬гғӯгғҜгӮігғӣгғўгғӯгӮёгғјгҒ®иҰ–зӮ№гҒӢгӮүгҖҒгӮ№гғ”гғҺгғ«гғҺгғ«гғ гҒҜгӮігғӣгғўгғӯгӮёгғјгҒ®йҖЈзөҗжә–еҗҢеһӢгҒ§гҒӮгӮӢгҖӮ1 гҒ®е№іж–№ж №гҒ®д»Јж•°зҫӨпјҲжЁҷж•°гҒҢ 2 гҒ§гҒӘгҒ„дҪ“дёҠгҒқгӮҢгҒҜеӨ§йӣ‘жҠҠгҒ«гҒҜиҮӘжҳҺгҒӘгӮ¬гғӯгғҜдҪңз”ЁгӮ’жҢҒгҒЈгҒҹ 2 е…ғзҫӨгҒЁеҗҢгҒҳгҒ§гҒӮгӮӢпјүгӮ’ Ој2 гҒЁжӣёгҒҸгҒЁгҖҒзҹӯе®Ңе…ЁеҲ— гҒҜгӮігғӣгғўгғӯгӮёгғјгҒ®й•·е®Ңе…ЁеҲ—гӮ’з”ҹгҒҝеҮәгҒ—гҖҒгҒқгӮҢгҒҜ гҒ§е§ӢгҒҫгӮӢгҖӮK гҒ«дҝӮж•°гӮ’жҢҒгҒӨд»Јж•°зҫӨгҒ® 0 ж¬ЎгӮ¬гғӯгғҜгӮігғӣгғўгғӯгӮёгғјзҫӨгҒҜеҚҳгҒ« K-еҖӨзӮ№гҒ®зҫӨгҒ§гҒӮгӮӢпјҡ H0(G; K) = G(K)гҖҒгҒҠгӮҲгҒі H1(Ој2; K) вү… K*/K*2, гӮҲгҒЈгҒҰеүҚгҒ®еҲ—гӮ’еҫ©е…ғгҒҷгӮӢпјҡ гҒҹгҒ гҒ—гӮ№гғ”гғҺгғ«гғҺгғ«гғ гҒҜйҖЈзөҗжә–еҗҢеһӢ H0(OV; K) вҶ’ H1(Ој2; K) гҒ§гҒӮгӮӢгҖӮ гӮ№гғ”гғізҫӨгҒЁгғ”гғізҫӨжң¬зҜҖгҒ«гҒҠгҒ„гҒҰ V гҒҜжңүйҷҗж¬Ўе…ғгҒ§гҒӮгӮҠгҒқгҒ®еҸҢз·ҡеһӢеҪўејҸгҒҜйқһзү№з•°гҒ§гҒӮгӮӢгҒЁд»®е®ҡгҒҷгӮӢгҖӮпјҲK гҒҢжЁҷж•° 2 гҒ§гҒӮгӮҢгҒ°гҒ“гӮҢгҒҜ V гҒ®ж¬Ўе…ғгҒҢеҒ¶ж•°гҒ§гҒӮгӮӢгҒ“гҒЁгӮ’еҗ«гӮҖгҖӮпјү гғ”гғізҫӨ PinV(K) гҒҜгӮ№гғ”гғҺгғ«гғҺгғ«гғ Вұ1 гҒ®е…ғгҒ®гӮҜгғӘгғ•гӮ©гғјгғүзҫӨ О“ гҒ®йғЁеҲҶзҫӨгҒ§гҒӮгӮҠгҖҒеҗҢж§ҳгҒ«гӮ№гғ”гғізҫӨ SpinV(K) гҒҜ PinV(K) гҒ«гҒҠгҒ„гҒҰгғҮгӮЈгӮҜгӮҪгғідёҚеӨүйҮҸ 0 гҒ®е…ғгҒ®йғЁеҲҶзҫӨгҒ§гҒӮгӮӢгҖӮжЁҷж•°гҒҢ 2 гҒ§гҒӘгҒ„гҒЁгҒҚгҖҒгҒ“гӮҢгӮүгҒҜиЎҢеҲ—ејҸ 1 гҒ®е…ғгҒ§гҒӮгӮӢгҖӮгӮ№гғ”гғізҫӨгҒҜйҖҡеёёгғ”гғізҫӨгҒ«гҒҠгҒ„гҒҰжҢҮж•° 2 гӮ’жҢҒгҒӨгҖӮ гӮҜгғӘгғ•гӮ©гғјгғүзҫӨгҒӢгӮүзӣҙдәӨзҫӨгҒёгҒ®е…Ёе°„жә–еҗҢеһӢгҒҢеӯҳеңЁгҒҷгӮӢгҒ“гҒЁгӮ’зӣҙеүҚгҒ®гӮ»гӮҜгӮ·гғ§гғігҒӢгӮүжҖқгҒ„еҮәгҒқгҒҶгҖӮзү№ж®ҠзӣҙдәӨзҫӨгӮ’ О“0 гҒ®еғҸгҒЁгҒ—гҒҰе®ҡзҫ©гҒҷгӮӢгҖӮK гҒ®жЁҷж•°гҒҢ 2 гҒ§гҒӘгҒ‘гӮҢгҒ°гҒ“гӮҢгҒҜеҚҳгҒ«зӣҙдәӨзҫӨгҒ®иЎҢеҲ—ејҸ 1 гҒ®е…ғгҒ®зҫӨгҒ§гҒӮгӮӢгҖӮK гҒ®жЁҷж•°гҒҢ 2 гҒ§гҒӮгӮҢгҒ°гҖҒзӣҙдәӨзҫӨгҒ®гҒҷгҒ№гҒҰгҒ®е…ғгҒҜиЎҢеҲ—ејҸ 1 гӮ’гӮӮгҒЎгҖҒзү№ж®ҠзӣҙдәӨзҫӨгҒҜгғҮгӮЈгӮҜгӮҪгғідёҚеӨүйҮҸ 0 гҒ®е…ғгҒ®йӣҶеҗҲгҒ§гҒӮгӮӢгҖӮ гғ”гғізҫӨгҒӢгӮүзӣҙдәӨзҫӨгҒёгҒ®жә–еҗҢеһӢгҒҢеӯҳеңЁгҒҷгӮӢгҖӮеғҸгҒҜгӮ№гғ”гғҺгғ«гғҺгғ«гғ 1 вҲҲ K*/K*2 гҒ®е…ғгҒӢгӮүгҒӘгӮӢгҖӮж ёгҒҜе…ғ +1 гҒЁ вҲ’1 гҒӢгӮүгҒӘгӮҠгҖҒK гҒ®жЁҷж•°гҒҢ 2 гҒ§гҒӘгҒ‘гӮҢгҒ°дҪҚж•° 2 гӮ’гӮӮгҒӨгҖӮеҗҢж§ҳгҒ«гӮ№гғ”гғізҫӨгҒӢгӮү V гҒ®зү№ж®ҠзӣҙдәӨзҫӨгҒёгҒ®жә–еҗҢеһӢгҒҢеӯҳеңЁгҒҷгӮӢгҖӮ V гҒҢе®ҹж•°дёҠжӯЈгҒӮгӮӢгҒ„гҒҜиІ е®ҡеҖӨз©әй–“гҒ§гҒӮгӮӢе…ұйҖҡгҒ®е ҙеҗҲгҒ«гҒҠгҒ„гҒҰгҖҒгӮ№гғ”гғізҫӨгҒҜзү№ж®ҠзӣҙдәӨзҫӨгҒ®дёҠгҒёгҒЁеҶҷгӮҠ V гҒ®ж¬Ўе…ғгҒҢе°‘гҒӘгҒҸгҒЁгӮӮ 3 гҒ§гҒӮгӮҢгҒ°еҚҳйҖЈзөҗгҒ§гҒӮгӮӢгҖӮгҒ•гӮүгҒ«гҒ“гҒ®жә–еҗҢеһӢгҒ®ж ёгҒҜ 1 гҒЁ вҲ’1 гҒӢгӮүгҒӘгӮӢгҖӮгҒӘгҒ®гҒ§гҒ“гҒ®е ҙеҗҲгӮ№гғ”гғізҫӨ Spin(n) гҒҜ SO(n) гҒ®дәҢйҮҚиў«иҰҶгҒ§гҒӮгӮӢгҖӮгҒ—гҒӢгҒ—гҒӘгҒҢгӮүгҖҒгӮ№гғ”гғізҫӨгҒ®еҚҳйҖЈзөҗжҖ§гҒҜдёҖиҲ¬гҒ«гҒҜжӯЈгҒ—гҒҸгҒӘгҒ„гҒ“гҒЁгҒ«жіЁж„ҸгҒ—гҒҰгҒҸгҒ гҒ•гҒ„пјҡ V гҒҢгҒЁгӮӮгҒ« 2 д»ҘдёҠгҒ® p, q гҒ«еҜҫгҒ—гҒҰ Rp,q гҒ§гҒӮгӮҢгҒ°гӮ№гғ”гғізҫӨгҒҜеҚҳйҖЈзөҗгҒ§гҒҜгҒӘгҒ„гҖӮгҒ“гҒ®е ҙеҗҲд»Јж•°зҫӨ Spinp,q гҒҜд»Јж•°зҫӨгҒЁгҒ—гҒҰеҚҳйҖЈзөҗгҒ§гҒӮгӮӢгҖӮгҒқгҒ®е®ҹж•°еҖӨзӮ№гҒ®зҫӨ Spinp,q(R) гҒҜеҚҳйҖЈзөҗгҒ§гҒӘгҒ„гҒ«гӮӮгҒӢгҒӢгӮҸгӮүгҒҡгҖӮгҒ“гӮҢгҒҜгҒӢгҒӘгӮҠеҫ®еҰҷгҒӘзӮ№гҒ§гҒӮгӮҠгҖҒе°‘гҒӘгҒҸгҒЁгӮӮ 1 еҶҠгҒ®гӮ№гғ”гғізҫӨгҒ«гҒӨгҒ„гҒҰгҒ®жЁҷжә–зҡ„гҒӘжң¬гҒ®и‘—иҖ…гӮ’гҒҷгҒЈгҒӢгӮҠж··д№ұгҒ•гҒӣгҒҹгҖӮ гӮ№гғ”гғҺгғ«гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•° Cв„“p,q(C) гҒ§ p + q = 2n гҒЁеҒ¶ж•°гҒ«гҒӘгӮӢгӮӮгҒ®гҒҜ 2n ж¬Ўе…ғгҒ®иӨҮзҙ иЎЁзҸҫгӮ’жҢҒгҒӨиЎҢеҲ—д»Јж•°гҒ§гҒӮгӮӢгҖӮзҫӨ Pinp,q(R) гҒ«еҲ¶йҷҗгҒҷгӮӢгҒ“гҒЁгҒ«гӮҲгӮҠеҗҢгҒҳж¬Ўе…ғгҒ® Pin зҫӨгҒ®иӨҮзҙ иЎЁзҸҫгӮ’еҫ—гҖҒгҒ“гӮҢгҒҜгӮ№гғ”гғіиЎЁзҸҫгҒЁе‘јгҒ°гӮҢгӮӢгҖӮгҒ“гӮҢгӮ’гӮ№гғ”гғізҫӨ Spinp,q(R) гҒ«еҲ¶йҷҗгҒҷгӮҢгҒ°ж¬Ўе…ғ 2nвҲ’1 гҒ® 2 гҒӨгҒ®еҚҠгӮ№гғ”гғіиЎЁзҸҫпјҲгҒӮгӮӢгҒ„гҒҜгғҜгӮӨгғ«иЎЁзҸҫпјүгҒ®е’ҢгҒЁгҒ—гҒҰеҲҶи§ЈгҒҷгӮӢгҖӮ p + q = 2n + 1 гҒЁеҘҮж•°гҒ«гҒӘгӮҢгҒ°гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•° Cв„“p,q(C) гҒҜгҒқгӮҢгҒһгӮҢгҒҢ 2n ж¬Ўе…ғгҒ®иЎЁзҸҫгӮ’жҢҒгҒЈгҒҰгҒ„гӮӢгӮҲгҒҶгҒӘ 2 гҒӨгҒ®иЎҢеҲ—д»Јж•°гҒ®е’ҢгҒ§гҒӮгӮҠгҖҒгҒ“гӮҢгӮүгӮӮгҒҫгҒҹдёЎж–№гҒЁгӮӮгғ”гғізҫӨ Pinp,q(R) гҒ®иЎЁзҸҫгҒ§гҒӮгӮӢгҖӮгӮ№гғ”гғізҫӨ Spinp,q(R) гҒёгҒ®еҲ¶йҷҗдёҠгҒ“гӮҢгӮүгҒҜеҗҢеһӢгҒ«гҒӘгӮҠгҖҒгҒ—гҒҹгҒҢгҒЈгҒҰгӮ№гғ”гғізҫӨгҒҜж¬Ўе…ғ 2n гҒ®иӨҮзҙ гӮ№гғ”гғҺгғ«иЎЁзҸҫгӮ’жҢҒгҒӨгҖӮ гӮҲгӮҠдёҖиҲ¬гҒ«гҖҒд»»ж„ҸгҒ®дҪ“дёҠгҒ®гӮ№гғ”гғҺгғ«зҫӨгҒЁгғ”гғізҫӨгҒҜжӯЈзўәгҒӘж§ӢйҖ гҒҢеҜҫеҝңгҒҷгӮӢгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®ж§ӢйҖ гҒ«дҫқеӯҳгҒҷгӮӢеҗҢж§ҳгҒ®иЎЁзҸҫгӮ’жҢҒгҒӨпјҡгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒҢгҒӮгӮӢеҸҜйҷӨд»Јж•°дёҠгҒ®иЎҢеҲ—д»Јж•°гҒ§гҒӮгӮӢеӣ еӯҗгӮ’жҢҒгҒӨгҒЁгҒҚгҒ«гҒҜгҒ„гҒӨгҒ§гӮӮгҒқгҒ®еҸҜйҷӨд»Јж•°дёҠгҒ®гғ”гғігҒЁгӮ№гғ”гғізҫӨгҒ®еҜҫеҝңгҒҷгӮӢиЎЁзҸҫгӮ’еҫ—гӮӢгҖӮдҫӢгҒҲгҒ°е®ҹж•°дҪ“дёҠгҒ®е ҙеҗҲгҒ«гҒӨгҒ„гҒҰгҒҜгӮ№гғ”гғҺгғјгғ«гҒ®иЁҳдәӢгӮ’иҰӢгӮҲгҖӮ е®ҹгӮ№гғ”гғҺгғ«вҶ’и©ізҙ°гҒҜгҖҢгӮ№гғ”гғҺгғјгғ«гҖҚгӮ’еҸӮз…§
е®ҹгӮ№гғ”гғіиЎЁзҸҫгӮ’иЁҳиҝ°гҒҷгӮӢгҒҹгӮҒгҒ«гҖҒгӮ№гғ”гғізҫӨгҒҢгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®дёӯгҒ«гҒ©гҒ®гӮҲгҒҶгҒ«гҒӮгӮӢгҒӢгӮ’зҹҘгӮүгҒӘгҒ‘гӮҢгҒ°гҒӘгӮүгҒӘгҒ„гҖӮгғ”гғізҫӨ Pinp,q гҒҜеҚҳдҪҚгғҷгӮҜгғҲгғ«гҒ®з©ҚгҒЁгҒ—гҒҰжӣёгҒ‘гӮӢ Cв„“p,q гҒ®еҸҜйҖҶе…ғгҒ®йӣҶеҗҲгҒ§гҒӮгӮӢпјҡ гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®дёҠгҒ®е…·дҪ“зҡ„гҒӘе®ҹзҸҫгҒЁжҜ”гҒ№гҒҰгҖҒгғ”гғізҫӨгҒҜд»»ж„ҸгҒ«гҒҹгҒҸгҒ•гӮ“гҒ®йҸЎжҳ гҒ®з©ҚгҒ«еҜҫеҝңгҒҷгӮӢпјҡ гҒқгӮҢгҒҜе…ЁзӣҙдәӨзҫӨ O(p, q) гҒ®иў«иҰҶгҒ§гҒӮгӮӢгҖӮгӮ№гғ”гғізҫӨгҒҜеҚҳдҪҚгғҷгӮҜгғҲгғ«гҒ®еҒ¶ж•°еҖӢгҒ®з©ҚгҒ§гҒӮгӮӢгӮҲгҒҶгҒӘ Pinp,q гҒ®е…ғгҒӢгӮүгҒӘгӮӢгҖӮгҒ—гҒҹгҒҢгҒЈгҒҰгӮ«гғ«гӮҝгғігғ»гғҮгғҘгғүгғҚгҒ®е®ҡзҗҶгҒ«гӮҲгҒЈгҒҰ Spin гҒҜеӣәжңүеӣһи»ўгҒ®зҫӨ SO(p, q) гҒ®иў«иҰҶгҒ§гҒӮгӮӢгҖӮ Оұ: Cв„“ вҶ’ Cв„“ гӮ’ pure гғҷгӮҜгғҲгғ«гҒ«дҪңз”ЁгҒҷгӮӢеҶҷеғҸ v вҶҰ вҲ’v гҒ«гӮҲгҒЈгҒҰдёҺгҒҲгӮүгӮҢгӮӢиҮӘе·ұеҗҢеһӢгҒЁгҒҷгӮӢгҖӮгҒҷгӮӢгҒЁзү№гҒ« Spinp,q гҒҜе…ғгҒҢ Оұ гҒ«гӮҲгҒЈгҒҰеӣәе®ҡгҒ•гӮҢгӮӢ Pinp,q гҒ®йғЁеҲҶзҫӨгҒ§гҒӮгӮӢгҖӮ гҒЁгҒҷгӮӢгҖӮпјҲгҒ“гӮҢгӮүгҒҜ Cв„“p,q гҒ«гҒҠгҒ„гҒҰгҒЎгӮҮгҒҶгҒ©еҒ¶ж•°ж¬ЎгҒ®е…ғгҒ§гҒӮгӮӢгҖӮпјүгҒҷгӮӢгҒЁгӮ№гғ”гғізҫӨгҒҜ Cв„“ 0 Cв„“p,q гҒ®ж—ўзҙ„иЎЁзҸҫгҒҜгғ”гғізҫӨгҒ®иЎЁзҸҫгӮ’дёҺгҒҲгӮӢгҒҹгӮҒгҒ«еҲ¶йҷҗгҒҷгӮӢгҖӮйҖҶгҒ«гҖҒгғ”гғізҫӨгҒҜеҚҳдҪҚгғҷгӮҜгғҲгғ«гҒ§з”ҹжҲҗгҒ•гӮҢгӮӢгҒӢгӮүгҖҒгҒқгҒ®ж—ўзҙ„иЎЁзҸҫгҒ®гҒҷгҒ№гҒҰгҒҜгҒ“гҒ®гӮҲгҒҶгҒ«гҒ—гҒҰиӘҳе°ҺгҒ•гӮҢгӮӢгҖӮгҒ—гҒҹгҒҢгҒЈгҒҰ 2 гҒӨгҒ®иЎЁзҸҫгҒҜдёҖиҮҙгҒҷгӮӢгҖӮеҗҢгҒҳзҗҶз”ұгҒ®гҒҹгӮҒгҖҒгӮ№гғ”гғігҒ®ж—ўзҙ„иЎЁзҸҫгҒҜ Cв„“ p,q гғ”гғіиЎЁзҸҫгӮ’еҲҶйЎһгҒҷгӮӢгҒҹгӮҒгҒ«гҒҜгҖҒгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®еҲҶйЎһгҒ«гӮўгғ”гғјгғ«гҒҷгӮӢгҒ гҒ‘гҒ§гӮҲгҒ„гҖӮпјҲеҒ¶йғЁеҲҶд»Јж•°гҒ®иЎЁзҸҫгҒ§гҒӮгӮӢпјүгӮ№гғ”гғіиЎЁзҸҫгӮ’иҰӢгҒӨгҒ‘гӮӢгҒҹгӮҒгҒ«гҒҜгҖҒгҒҫгҒҡж¬ЎгҒ®еҗҢеһӢгҒ®гҒ„гҒҡгӮҢгҒӢгӮ’еҲ©з”ЁгҒ§гҒҚгӮӢпјҲдёҠиЁҳеҸӮз…§пјү
гҒқгҒ—гҒҰз¬ҰеҸ· (p, q вҲ’ 1) гҒӮгӮӢгҒ„гҒҜ (q, p вҲ’ 1) гҒ«гҒҠгҒ‘гӮӢгғ”гғіиЎЁзҸҫгҒЁгҒ—гҒҰз¬ҰеҸ· (p, q) гҒ«гҒҠгҒ‘гӮӢгӮ№гғ”гғіиЎЁзҸҫгӮ’е®ҹзҸҫгҒ§гҒҚгӮӢгҖӮ еҝңз”Ёеҫ®еҲҶе№ҫдҪ•еӯҰеӨ–з©Қд»Јж•°гҒ®дё»иҰҒгҒӘеҝңз”ЁгҒ®дёҖгҒӨгҒҜеҫ®еҲҶе№ҫдҪ•еӯҰгҒ«гҒӮгӮҠгҒқгҒ“гҒ§гҒҜгҒқгӮҢгҒҢж»‘гӮүгҒӢгҒӘеӨҡж§ҳдҪ“дёҠгҒ®еҫ®еҲҶеҪўејҸгҒ®гғ•гӮЎгӮӨгғҗгғјжқҹгӮ’е®ҡзҫ©гҒҷгӮӢгҒҹгӮҒгҒ«дҪҝгӮҸгӮҢгӮӢгҖӮпјҲ擬пјүгғӘгғјгғһгғіеӨҡж§ҳдҪ“гҒ®е ҙеҗҲгҒ«гҒҜгҖҒжҺҘз©әй–“гҒҜиЁҲйҮҸгҒ«гӮҲгҒЈгҒҰиӘҳе°ҺгҒ•гӮҢгӮӢиҮӘ然гҒӘдәҢж¬ЎеҪўејҸгӮ’жҢҒгҒӨгҖӮгҒ—гҒҹгҒҢгҒЈгҒҰгҖҒеӨ–жқҹгҒЁгҒ®гӮўгғҠгғӯгӮёгғјгҒ§гӮҜгғӘгғ•гӮ©гғјгғүжқҹгӮ’е®ҡзҫ©гҒ§гҒҚгӮӢгҖӮгҒ“гӮҢгҒҜгғӘгғјгғһгғіе№ҫдҪ•еӯҰгҒ«гҒҠгҒ„гҒҰгҒҹгҒҸгҒ•гӮ“гҒ®йҮҚиҰҒгҒӘеҝңз”ЁгӮ’жҢҒгҒӨгҖӮгҒҠгҒқгӮүгҒҸгӮҲгӮҠйҮҚиҰҒгҒӘгҒ®гҒҜгӮ№гғ”гғіеӨҡж§ҳдҪ“гҖҒгҒқгҒ®д»ҳйҡҸгҒҷгӮӢгӮ№гғ”гғҺгғ«жқҹгҒқгҒ—гҒҰ spinc еӨҡж§ҳдҪ“гҒёгҒ®гҒӨгҒӘгҒҢгӮҠгҒ§гҒӮгӮҚгҒҶгҖӮ зү©зҗҶеӯҰгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒҜзү©зҗҶеӯҰгҒ«гҒҠгҒ„гҒҰгҒҹгҒҸгҒ•гӮ“гҒ®йҮҚиҰҒгҒӘеҝңз”ЁгӮ’жҢҒгҒӨгҖӮзү©зҗҶеӯҰиҖ…гҒҜйҖҡеёёгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гӮ’ж¬ЎгҒ®жҖ§иіӘгӮ’жҢҒгҒӨгғҮгӮЈгғ©гғғгӮҜиЎҢеҲ—гҒЁе‘јгҒ°гӮҢгӮӢиЎҢеҲ— Оі0, вҖҰ, Оі3 гҒ«гӮҲгҒЈгҒҰз”ҹжҲҗгҒ•гӮҢгҒҹеҹәеә•гӮ’жҢҒгҒӨд»Јж•°гҒЁиҖғгҒҲгӮӢгҖӮ гҒҹгҒ гҒ— О· гҒҜз¬ҰеҸ· (1, 3) гҒ®дәҢж¬ЎеҪўејҸгҒ®иЎҢеҲ—гҒ§гҒӮгӮӢгҖӮгҒ“гӮҢгӮүгҒҜгҒЎгӮҮгҒҶгҒ©пјҲйҮҚиҰҒгҒ§гҒӘгҒ„еӣ еӯҗ 2 гӮ’йҷӨгҒ„гҒҰпјүгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•° Cв„“1,3(R) гҒ®е®ҡзҫ©й–ўдҝӮејҸгҒ§гҒӮгӮҠгҖҒгҒқгҒ®иӨҮзҙ еҢ–гҒҜ Cв„“1,3(R)C гҒ§гҒӮгӮҠгҒ“гӮҢгҒҜгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®еҲҶйЎһгҒ«гӮҲгҒЈгҒҰиӨҮзҙ 4ж¬ЎиЎҢеҲ—гҒ®д»Јж•°гҒ«еҗҢеһӢгҒ§гҒӮгӮӢгҖӮ гғҮгӮЈгғ©гғғгӮҜиЎҢеҲ—гҒҜжңҖеҲқгғқгғјгғ«гғ»гғҮгӮЈгғ©гғғгӮҜгҒ«гӮҲгҒЈгҒҰгҖҒйӣ»еӯҗгҒ«еҜҫгҒҷгӮӢзӣёеҜҫи«–гҒ®дёҖйҡҺжіўеӢ•ж–№зЁӢејҸгӮ’жӣёгҒҚгҖҒгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒӢгӮүиӨҮзҙ иЎҢеҲ—гҒёгҒ®жҳҺзӨәзҡ„гҒӘеҗҢеһӢгӮ’дёҺгҒҲгӮҲгҒҶгҒЁгҒ—гҒҰгҒ„гҒҹжҷӮгҒ«гҖҒжӣёгҒҚдёӢгҒ•гӮҢгҒҹгҖӮзөҗжһңгҒҜгғҮгӮЈгғ©гғғгӮҜж–№зЁӢејҸгӮ’е®ҡзҫ©гҒ—гғҮгӮЈгғ©гғғгӮҜдҪңз”Ёзҙ гӮ’е°Һе…ҘгҒҷгӮӢгҒҹгӮҒгҒ«з”ЁгҒ„гӮүгӮҢгҒҹгҖӮгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°е…ЁдҪ“гҒҜгғҮгӮЈгғ©гғғгӮҜе ҙеҸҢз·ҡеһӢгҒ®еҪўејҸгҒ®е ҙгҒ®йҮҸеӯҗи«–гҒ«гҒҠгҒ„гҒҰзҸҫгӮҢгӮӢгҖӮ йҮҸеӯҗи«–гӮ’иЁҳиҝ°гҒҷгӮӢгҒҹгӮҒгҒ®гӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒ®дҪҝз”ЁгҒҜдёӯгҒ§гӮӮ Mario SchГ¶nberg[8]гҒ«гӮҲгҒЈгҒҰгҖҒgeometric calculus гҒ®иЁҖи‘үгҒ§гҒҜ David Hestenes гҒЁ Basil Hiley гҒЁ hierarchy of Clifford algebras гҒ®е…ұеҗҢз ”з©¶иҖ…гҒ«гӮҲгҒЈгҒҰгҖҒгҒқгҒ—гҒҰ Elio Conte et al.[9][10]гҒ«гӮҲгҒЈгҒҰйҖІгӮҒгӮүгӮҢгҒҰгҒҚгҒҹгҖӮ гӮігғігғ”гғҘгғјгӮҝгғ“гӮёгғ§гғіжңҖиҝ‘гҖҒгӮҜгғӘгғ•гӮ©гғјгғүд»Јж•°гҒҜгӮігғігғ”гғҘгғјгӮҝгғ“гӮёгғ§гғігҒ«гҒҠгҒ‘гӮӢ action recognition гҒЁеҲҶйЎһгҒ®е•ҸйЎҢгҒ«гҒҠгҒ„гҒҰеҝңз”ЁгҒ•гӮҢгҒҰгҒ„гӮӢгҖӮRodriguez et al.[11] гҒҜдјқзөұзҡ„гҒӘ MACH п¬Ғlters гӮ’ video (3D spatiotemporal volume) гҒЁгӮӘгғ—гғҶгӮЈгӮ«гғ«гғ•гғӯгғјгҒ®гӮҲгҒҶгҒӘгғҷгӮҜгғҲгғ«еҖӨгғҮгғјгӮҝгҒ«дёҖиҲ¬еҢ–гҒҷгӮӢгӮҜгғӘгғ•гӮ©гғјгғүеҹӢгӮҒиҫјгҒҝгӮ’жҸҗжЎҲгҒҷгӮӢгҖӮгғҷгӮҜгғҲгғ«еҖӨгғҮгғјгӮҝгҒҜ Clifford Fourier Transform гӮ’з”ЁгҒ„гҒҰи§ЈжһҗгҒ•гӮҢгӮӢгҖӮгҒ“гӮҢгӮүгҒ®гғҷгӮҜгғҲгғ«гҒ«еҹәгҒҘгҒ„гҒҰгӮўгӮҜгӮ·гғ§гғігғ•гӮЈгғ«гӮҝгғјгҒҜгӮҜгғӘгғ•гӮ©гғјгғүгғ•гғјгғӘгӮЁгғүгғЎгӮӨгғігҒ«гҒҠгҒ„гҒҰгӮ·гғігӮ»гӮөгӮӨгӮәгҒ•гӮҢгӮўгӮҜгӮ·гғ§гғігҒ®иӘҚиӯҳгҒҜ Clifford Correlation гӮ’з”ЁгҒ„гҒҰе®ҹиЎҢгҒ•гӮҢгӮӢгҖӮи‘—иҖ…гҒҜеҸӨе…ёзҡ„зү№еҫҙгғ•гӮЈгғ«гғ гҒЁгӮ№гғқгғјгғ„е ұйҒ“гғҶгғ¬гғ“гҒ«гҒҠгҒ„гҒҰе…ёеһӢзҡ„гҒ«е®ҹиЎҢгҒ•гӮҢгӮӢгӮўгӮҜгӮ·гғ§гғігӮ’иӘҚиӯҳгҒҷгӮӢгҒ“гҒЁгҒ«гӮҲгҒЈгҒҰгӮҜгғӘгғ•гӮ©гғјгғүеҹӢгӮҒиҫјгҒҝгҒ®жңүеҠ№жҖ§гӮ’иӘ¬жҳҺгҒҷгӮӢгҖӮ й–ўйҖЈй …зӣ®
и„ҡжіЁжіЁйҮҲ
еҮәе…ё
еҸӮиҖғж–ҮзҢ®
й–ўйҖЈж–ҮзҢ®
еӨ–йғЁгғӘгғігӮҜ
|
Portal di Ensiklopedia Dunia

















































































