シュタイナーの円鎖

幾何学において、シュタイナーの円鎖^[1]（シュタイナーのえんさ、英: Steiner chain）または シュタイナー環^[2]、シュタイナーの円環^[3]、シュタイナー円鎖^[4]^[5]^[6]は、 $n$ 個の円がある2つの交わらない円と円鎖の前後の円とに接しているとき、その $n$ 個の円の集合を指す用語である。ただし $n$ は有限の正整数であるとする。特に閉じた円鎖（closed chain）とは最初の円と最後（ $n$ 個目の）円が接する状態にあることを指す。逆に open chain とは、最初と最後の円が接していない場合を表す。

与円 $α, β$ （図1の赤と青の円）は交差しないこと以外の制約を受けない。つまり、必ずしも一方の円がもう一方の円の内部にあるとは限らない。シュタイナーの円鎖の円の中心の軌跡は、一方の円がもう一方の円の内部にあるならば楕円を、そうでないならば双曲線を成す。和算では、一方の円がもう一方の円を内包している図において、外側の円を外円、内側の円を内円と呼んでいる^[7]。

シュタイナーの円鎖はヤコブ・シュタイナーの名を冠している。シュタイナーの功績の一つに Steiner's porism と呼ばれる次の性質を持つ図形がある。

2つの円 $α, β$ に対して、 $n$ 個の円の閉じているシュタイナーの円鎖が一つでもあれば、 $n$ 個の円の閉じているシュタイナーの円鎖は無数に見つけることができる。そして $α, β$ に接する円はすべて、そのようなシュタイナーの円鎖の一つになり得る^{[注釈 1]}。

反転幾何学はシュタイナーの円鎖をうまく扱うのに有用である。反転は交点、角、円を一対一対応させる。 $n$ 個の円の成すシュタイナーの円鎖は反転によって別の $n$ 個の円に移る。特定の円による反転は円 $α, β$ を同心円に変換する。この際、シュタイナーの円鎖を構成する全ての円は同じ大きさとなり、玉軸受のようにアニュラス上を"転がる"ことができる。この構成がシュタイナーの円鎖の様々な性質をもたらしている。たとえば、シュタイナーの円鎖の円同士の接点は常に共円である。シュタイナーの円鎖の派生物には例えばソディの六球連鎖やパップス円鎖がある。

定義と接し方の種類

シュタイナーの円鎖の接し方の違い
7円のシュタイナーの円鎖 (黒)。赤い内部の円に外接し青い外部の円に内接している。
7円のシュタイナーの円鎖 (黒)。青と赤どちらの円にも外接している。
8円のシュタイナーの円鎖 (黒)。青と赤の円どちらにも内接している、あるいはどちらにも外接している。

2円 $α, β$ が交わっていなければ $α, β$ の配置は、小さい方の円が大きい方の円の内部にある場合と、外部にある場合のいずれかに限られる。通常、2円はアニュラスのように小さい円が大きい円の内部にある場合で表現される。この構成ではシュタイナーの円鎖は内側の円に外接し、外側の円に内接している。一方、小さい方の円が大きい円の外部にある場合も存在する。この場合も、シュタイナーの円鎖の条件を満たし、元の2円に外接のみ、または内接のみするようになる。

元の2円が接している場合は円鎖は無限となりアルベロスとともに議論されることが多い（パップス円鎖）。

円鎖の開閉

9つの円の円鎖が閉じている。
9つの円の円鎖が開いていて、一部が重なっている。
17つの円が二周することで多環を成している。

2つの円 $α, β$ は $n$ 個の円から成るシュタイナーの円鎖の円と接しているが、 $n$ 個の円の1つ $C k$ は $α, β$ と両隣の円の4つとしか接していない。通常は、シュタイナーの円鎖が閉じている場合を議論するが、そうでない場合、つまり $C 1, C n$ が接さない場合、 $C 1, C n$ は3円とだけ接することとなる。多環のシュタイナーの円鎖ではその円鎖が閉じる前にさらに何周かすることとなる。

シュタイナーの円鎖は双角錐のグラフにおける円充填定理の系である。

アニュラスと条件

アニュラスにおけるシュタイナーの円鎖
$n = 3$
$n = 6$
$n = 9$
$n = 12$
$n = 20$

最も単純なシュタイナーの円鎖は、2つの円 $α, β$ が同心円である場合に生成される。 $α, β$ の中心を $O$ とする。 $n$ 個の円から成るシュタイナーの円鎖について、2円 $α, β$ の大きい方の半径を $R$ 、小さい方の半径を $r$ 、隣り合うシュタイナーの円鎖の円の中心を $O i, O i + 1$ として対称性より、 $∠OiOOi + 1 = 2θ = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}360°/n$ である。また隣り合うシュタイナーの円鎖の円は接するので、円の中心の距離は円の半径 $ρ$ の2倍に等しい。図のように $∠ O i OO i +1 = 2 θ$ の角の二等分線は2つの直角三角形をつくるので $θ = 180° / n$ として、その正弦を求めることができる。

$\sin \theta ={\frac {\rho }{r+\rho }}$

よって $ρ$ について整理して次の式を得る。

$\rho ={\frac {r\sin \theta }{1-\sin \theta }}$

シュタイナーの円鎖のある円について、それぞれ $α, β$ との接点と、 $α, β$ の中心は明らかに共線であるから $R = r + 2 ρ$ が従う。

この等式によって、シュタイナーの円鎖の生成条件が与えられる。 $n$ 個の円から成るシュタイナーの円鎖ができる条件は、2円の半径 $R, r$ が次の式を満たすことである。

${\frac {R}{r}}=1+{\frac {2\sin \theta }{1-\sin \theta }}={\frac {1+\sin \theta }{1-\sin \theta }}=\left[\sec \theta +\tan \theta \right]^{2}$

次のように、半径の比は2円の反転距離によって、任意の円に拡張することができる。

$\delta =\ln {\frac {R}{r}}$

同心円の場合の解法を使って、一般の位置にある2円に対する $n$ 個の円から成るシュタイナーの円鎖ができる条件は以下のようにまとめられる^{[注釈 2]}。

$\delta =2\ln \left(\sec \theta +\tan \theta \right)=2\operatorname {gd} ^{-1}\theta$

$n$ 個の円から成るシュタイナーの円鎖が多環であるときは、アニュラスを $m$ 周するとして隣り合うシュタイナーの円鎖の円の中心の成す中心角が次の式を満たせばよい。

$\theta ={\frac {m}{n}}180^{\circ }$

換言すれば、シュタイナーの円鎖のできる条件は不変である。

反転下での性質

シュタイナーの円鎖の反転したものの性質
2円（桃と水）は元の円の両方に内接する。それらの円の中心は円の交点の成す中心角が $2 θ$ ならば、 $α, β$ の中心と共線である。
反転した図では、広義の円は広義の円へと移り、交点や角度を保つ。茶色の円は $α, β$ と直交している。
2つのシュタイナーの円鎖の隣り合う円の接点を通る円は最初の2円に直交する。
2つのシュタイナーの円鎖と与円の接点を通る円は元の2円に直交する。

円による反転は、シュタイナーの円鎖を同数の円を持つ他の図形に変換する。

円鎖の反転で、隣り合う円が接するという事実は変わらない。また、与円が同心円になるよう反転したとき、シュタイナーの円鎖の隣り合う円の接点は与円を反転したものの中間上にある。したがってシュタイナーの円鎖で、隣り合う円との接点は同一円周上にある。この方法はパップス円鎖にも適応できる。

反転された円鎖では、 $α, β$ の中心 $O$ からシュタイナー円鎖の円への接線は等角度で離れている。これは元の円鎖において反転の中心を通るシュタイナー円鎖の円の接線の成す角が常に等しいことを示している。

円鎖の反転で、元の円とシュタイナーの円鎖を成す円の接点と、その反対側の接点を結ぶ $n$ 本の直線はすべて一点 $O$ で交わる。同様に接点における接線も $O$ で交わる。反転の中心を通る直線は反転で自身に変換され、また接する・交わるといった状況などは不変であるので、上述した $2 n$ 本の直線に反転で対応する図形は一点で交わる。

無限個の族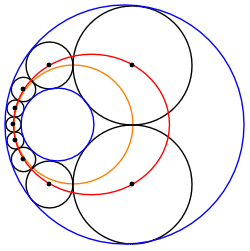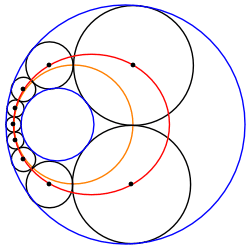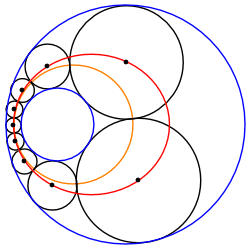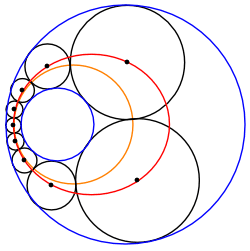

2つの円(青)について、1つでも閉じている円鎖が存在すれば、そのような円鎖は無限に存在する。

2つの交わらない円について、そのシュタイナーの円鎖を反転させたものをアニュラス上で"転がす"ことにより、別のシュタイナーの円鎖を作ることができる。ゆえに、2つの与円について、シュタイナーの円鎖が一つでも発見されれば、シュタイナーの円鎖は無限個ある。

中心の軌跡

シュタイナー円鎖を成す円の中心は常に円錐曲線上にある。例えば元の円の一方の円がもう一方の円の内部にある場合は楕円、外部にある場合は双曲線となる。これはアポロニウスの問題やパップス円鎖にも利用されている。3次元ではソディの六球連鎖に応用されている。

元の2円を $α, β$ 、その半径をそれぞれ $r α, r β$ 、中心をそれぞれ $A, B$ とする。ただし $α$ は $β$ の内部にあるとする。またシュタイナーの円鎖の $k$ 番目の円の円周、半径、直径、中心をそれぞれ $C k, r k, d β, P k$ とする。

${\overline {\mathbf {P} _{k}\mathbf {A} }}+{\overline {\mathbf {P} _{k}\mathbf {B} }}=(r_{\alpha }-r_{k})+\left(r_{\beta }+r_{k}\right)=r_{\alpha }+r_{\beta }$

$P k$ とそれぞれ $A, B$ の距離の和は常に $r α + r β$ となる。したがって、 $P k$ の軌跡は一定の楕円となる。特に、この楕円の焦点は $A, B$ となることが従う。

更にこの楕円の長軸 $a$ は次の式を満たす。

$2a=r_{\alpha }+r_{\beta }$

$p$ を $A, B$ の距離とすると、楕円の離心率 $e$ について次の式が成立する。

$e={\frac {p}{2a}}={\frac {p}{r_{\alpha }+r_{\beta }}}$

短軸を $b$ 、半直弦を $L$ とすれば次の式が成り立つ。

$b^{2}=a^{2}\left(1-e^{2}\right)=a^{2}-{\frac {p^{2}}{4}}$

$L={\frac {b^{2}}{a}}=a-{\frac {p^{2}}{4a}}$

したがって軌道の方程式は次のようになる。

$d={\frac {L}{1-e\cos \theta }}$

ここで $θ$ は軌跡を成す点が二つの焦点に対して成す角である。

円鎖の共役

n=4での円鎖の共役
赤と青の円に対する4円でのシュタイナーの円鎖
左図と同じではあるが最初の円を変えたもの
左図と同じではあるが最初の円を変えたもの

偶数個の円で構成されたシュタイナーの円鎖について、元の2円を円鎖の正反対の円としたとき、別の円鎖が構成されていると見なすことができる。元の円鎖が $n$ 個の円から成り $m$ 周期、与円を変えた後の円鎖が $p$ 個の円から成り $q$ 周期であるとすれば、次の式が成り立つ。

${\frac {m}{n}}+{\frac {p}{q}}={\frac {1}{2}}$

最も簡単なものは円鎖が4円で構成されていて周期が1の場合である。より一般的に、シュタイナーの円鎖を成す円はすべて4円と接して、与円2つは $n$ 個の円と接しているが、別の円を与円と見なしたとき、元の与円2つと円鎖を成す4円は、すべて4つの円と接している。したがって $m = q = 1, n = q = 4$ なので下の式のように式が成立していることが分かる。

${\frac {1}{4}}+{\frac {1}{4}}={\frac {1}{2}}$

一般化

シュタイナーの円鎖の自然な一般化として、与円が交わる場合を考える。一点で交わる、つまり接するときはパップス円鎖となる。パップス円鎖は無限個の円から成る。

ソディの六球連鎖は6円のシュタイナーの円鎖を3次元に一般化したものと考えられる。このとき六球の中心は同一円錐曲線、特に楕円上にある。六球の中心をある平面に固定したとき、六球連鎖の包絡線はデュパンのサイクライド（英語版）と呼ばれる図形となる。その反転はトーラスである。六球は与円にそれぞれ内接、外接するだけでなく他のある二球にも接している。

階層的な方法を用いて、更に別の一般化ができる。普通のシュタイナーの円鎖の2円が入れ子になっている、すなわち一方の円がもう一方の円に完全に内包される場合、シュタイナーの円鎖は大きい方の与円に内接している。階層的なシュタイナーの円鎖では、シュタイナーの円鎖のそれぞれの円はそれ自身が他のシュタイナーの円鎖の円に内接している。この過程を続けていくと、アポロニウスのギャスケットのようなフラクタルを作ることができる。

池田の定理

シュタイナーの円鎖に関連する結果に、池田の定理がある。池田貞一の名を冠する。

偶数個の円からなるシュタイナーの円鎖において、反対側に位置する2円の直径をそれぞれ $a, b$ としたとき $1 / a + 1 / b$ の値は一定である^[4]^[5]^[7]^[8]。

脚注

[脚注の使い方]

注釈

^ つまり新たに構成した任意のシュタイナーの円鎖の円は、元のシュタイナー鎖の円と同様に、他の2円に内接または外接するということ。
^ $\operatorname {gd} ^{-1}x$ は逆グーデルマン関数。

出典

^ 海野啓明「『美しい幾何学』書評：マオール，ヨスト共著，高木監訳，稲葉・河崎・田中・平澤・吉田訳」『形の科学会誌』第2巻第30号、形の科学会、2015年、115頁。
^ 森継, 修一「シュタイナー環におけるデカルトの円定理の拡張について」『数理解析研究所講究録』第1843号、2013年7月、155–162頁、CRID 1520009410039419392。
^ 石原諭. “シュタイナーの円環における半径の間の公式”. 2024年7月6日閲覧。
^ ^a ^b 平田, 浩一、四宮, 雅士「池田の定理の拡張について」『愛媛大学教育学部紀要』65巻、2019年4月、137-141頁。
^ ^a ^b 平田浩一「池田の定理の一般化と重心の役割について」『日本数学教育学会高専・大学部会論文誌』25巻、2014年9月。
^ 林雄一郎. “アルベロス図形と算額図形の数理”. izumi-math. 2024年7月6日閲覧。
^ ^a ^b 道脇, 義正、浜田, 敏男、大山, 誠「和算における一問題の解について」『科学史研究 12(108)』日本科学史学会、1972年、206頁。NDLJP:2380357。
^ 小曽根, 淳「Steiner chain と和算の環円問題再考」『RIMS Kôkyûroku Bessatsu』2018年、87-98頁。