„Éë„ÉÉ„Éó„Çπ„ÅÆÂÖ≠ËßíÂΩ¢ÂÆöÁêÜ  „Éë„ÉÉ„Éó„Çπ„ÅÆÂÆöÁêÜ„Åæ„Åü„ÅØ„Éë„ÉÉ„Éó„Çπ„ÅÆÂÖ≠ËßíÂΩ¢ÂÆöÁêÜÔºà„Éë„ÉÉ„Éó„Çπ„ÅÆ„Çç„Å£„Åã„Åè„Åë„ÅфŶ„ÅÑ„Çä„ÄÅËã±: Pappus's hexagon theoremÔºâ„Å®„ÅØ„Ç¢„ɨ„Ç≠„ǵ„É≥„Éâ„É™„Ç¢„ÅÆ„Éë„ÉÉ„Éó„Çπ„ÅÆÂêç„ÇíÂÜÝ„Åô„ÇãÂÆöÁêÜ„ÅƉ∏Ąŧ„Åß„ÅÇ„Çã[1]„ÄÇ
„Åì„ÅÆÂÆöÁêÜ„Å؉ªªÊÑè„ÅÆÂ∞ÑÂΩ±Âπ≥Èù¢‰∏ä„ÅßÊàêÁ´ã„Åô„Çã„Åå„ÄÅÈùûÂèØÊèõ‰Ωì‰∏ä„Åß„ÅØÊàêÁ´ã„Åó„Å™„ÅÑ[3]„ÄÇ„Éë„ÉÉ„Éó„Çπ„ÅÆÂÆöÁêÜ„ÅÆÊàê„ÇäÁ´ã„ŧÂ∞ÑÂΩ±Âπ≥Èù¢„ÅØ„Éë„ÉÉ„Éó„ÇπÂπ≥Èù¢Ôºàpappian planesÔºâ„Å®Â뺄Å∞„Çå„Çã„ÄÇ ÂÖàËø∞„ÅÆÂÖ≠ËßíÂΩ¢AbCaBc„Å´„ŧ„ÅфŶ„ÄÅAb ∥ aB, Bc ∥ bC„Å™„Çâ„Å∞Ôºà„Éë„ÉÉ„Éó„ÇπÁ∑öu„ÅØÁÑ°ÈôêÈÅÝÁõ¥Á∑ö„Å®„Å™„Å£„ŶԺâ2Áï™ÁõÆ„ÅÆÂõ≥„ÅÆÊßò„Å´„ÄÅ„Ç¢„Éï„Ç£„É≥Âπæ‰ΩïÂ≠¶„Å´„Åä„Åë„Çã„Éë„ÉÉ„Éó„Çπ„ÅÆÂÆöÁêÜ„ÇíÂæó„Çã„ÄÇ „Éë„ÉÉ„Éó„ÇπÁ∑öu„Å®Áõ¥Á∑ög, h„ÅåÂÖ±ÁÇπ„Å™„Çâ„Å∞„ÄÅlittle version of Pappus's theorem„ÇíÂæó„Çã[3][4]„ÄÇ ‰∫§ÁÇπÂÆöÁêÜ„Å´„Çà„Çå„Å∞„ÄÅÂÖ±ÁÇπ„Å™Áõ¥Á∑öA, B, C„Å®„ÄÅA, B, C„Å®„ÅØÁï∞„Å™„ÇãÁÇπ„ÅßÂÖ±ÁÇπ„Å™Áõ¥Á∑öa, b, c„Å´„Åä„ÅфŶ„ÄÅÁõ¥Á∑ö„ÅƉ∫§ÁÇπA ∩ b„Å®a ∩ B„ÇíÁµê„Å∂Áõ¥Á∑ö„ÇíX„ÄÅA ∩ c„Å®a ∩ C„ÇíÁµê„Å∂Áõ¥Á∑ö„Çíy„ÄÅB ∩ c„Å®b ∩ C„ÇíÁµê„Å∂Áõ¥Á∑ö„Çíz„Å®„Åô„Çå„Å∞„ÄÅx, y, z„ÅØÂÖ±ÁÇπ„Åß„ÅÇ„ÇãÔºà∩„Åß2Áõ¥Á∑ö„ÅƉ∫§ÁÇπ„ÇíÁ§∫„ÅôÔºâ„ÄÇ „Éë„ÉÉ„Éó„Çπ„ÅÆÂÆöÁêÜ„ÅØ„Éë„Çπ„Ç´„É´„ÅÆÂÆöÁêÜ„ÅÆÁâπÂà•„Å™ÂÝ¥Âêà„Åß„ÅÇ„Çã„ÄÇ„Éë„Çπ„Ç´„É´„ÅÆÂÆöÁêÜ„Å´Âá∫Áèæ„Åô„ÇãÂÜÜÈåêÊõ≤Á∑ö„Çí2Áõ¥Á∑ö„Å´ÈÄÄÂåñ„Åï„Åõ„Çå„Å∞„ÄÅ„Éë„ÉÉ„Éó„Çπ„ÅÆÂÆöÁêÜ„ÇíÂæó„Çã„ÄÇ„Éë„Çπ„Ç´„É´„ÅÆÂÆöÁêÜ„ÅØ„Åæ„Åü„ÄńDZ„ǧ„É™„ɺԺù„Éê„ÉÉ„Éè„É©„ÉÉ„Éè„ÅÆÂÆöÁêÜ„ÅÆÁâπÂà•„Å™ÂÝ¥Âêà„Åß„ÅÇ„Çã„ÄÇ „Éë„ÉÉ„Éó„ÇπÈÖçÁΩÆ„ÅØ„Éë„ÉÉ„Éó„Çπ„ÅÆÂÆöÁêÜ„Å´Âá∫Áèæ„Åô„Çã9„ŧ„ÅÆÁÇπ„Å®Áõ¥Á∑ö„ÅÆÈÖçÁΩÆ„Åß„ÅÇ„Çã„Älj∏ÄË਄Ŵ„ÅØ„ÄÅ„Éë„ÉÉ„Éó„ÇπÁ∑ö„ÅØÁõ¥Á∑öABC„Å®abc„ÅƉ∫§ÁÇπ„ÇíÈÄö„Çâ„Å™„ÅÑ[Ê≥®Èáà 1]„ÄÇ „Åì„ÅÆÈÖçÁΩÆ„ÅØËá™Â∑±ÂèåÂØæÊÄß„ÇíÊåńŧ„ÄÇ„Åó„Åü„Åå„Å£„ŶÁõ¥Á∑öBc, bC, XY„ÅØx, y, z„ÅÆ„Çà„ÅÜ„Å™ÂèåÂØæ„ÅÆÊÄßË≥™„ÇíÊåÅ„Å°„ÄÅX, Y, Z„ÅÆÂÖ±Á∑ö„ÅØBc, bC, XY„ÅÆÂÖ±ÁÇπ„Å®ÂØæÂøú„Åô„Çã„ÄÇ„Éë„ÉÉ„Éó„ÇπÈÖçÁΩÆ„ÅƄɨ„É¥„Ç£„Ç∞„É©„Éï„ÅØ„Éë„ÉÉ„Éó„Çπ„Ç∞„É©„Éï„Å®Â뺄Å∞„Çå„Çã„ÄÇ„Éë„ÉÉ„Éó„Çπ„Ç∞„É©„Éï„ÅØ18ÂÄã„ÅÆÈÝÇÁÇπ„Å®27ÂÄã„ÅÆËæ∫„ÇíÊåńŧ2ÈÉ®„ÅÆË∑ùÈõ¢Ê≠£Ââá„Å™„Ç∞„É©„Éï„Åß„ÅÇ„Çã„ÄÇ Ë®ºÊòé „Ç¢„Éï„Ç£„É≥ÂΩ¢Âºè„Åß„ÄÅ„ÅÇ„ÇãÂ∫ßÊ®ôË®≠ÂÆö„Åß„ÅÆ„Éë„ÉÉ„Éó„Çπ„ÅÆÂÆöÁêÜ„ÅåË®ºÊòé„Åï„Çå„Çå„Å∞„ÄÅ„Åù„Çå„ÇíÈÅ©ÂΩì„Å´Â∞ÑÂΩ±„Åô„Çã„Åì„Å®„Åß„Äʼn∏ÄË਄ÅÆ„Éë„ÉÉ„Éó„Çπ„ÅÆÂÆöÁêÜ„ÇíË®ºÊòé„Åß„Åç„Çã„ÄÇ „Ç¢„Éï„Ç£„É≥Âπ≥Èù¢„Åß„ÅØg ∦ h„Å®g ∥ h„ÇíÂå∫Âà•„Åô„ÇãÂøÖ˶ńÅå„ÅÇ„Çã„ÄÇ„Åæ„Åü„ÄÅÂçòÁ¥î„řˮºÊòé„ÅÆ„Åü„ÇÅ„Å´„ÅØ„ÄÅÂ∫ßÊ®ôË®≠ÂÆö„ÇíÂ∑ß„ÅèË°å„Çè„Å™„Åë„Çå„Å∞„Å™„Çâ„Å™„ÅÑ„ÄÇ ÂÝ¥Âêà1: g, h„ÅåÁÇπS = g ∩ h„Å߉∫§„Çè„ÇãÂÝ¥Âêà„ÄÇÂõ≥„ÅÆÊßò„Å´Â∫ßÊ®ô„ÇíË®≠ÂÆö„Åô„Çã„ÄÇ
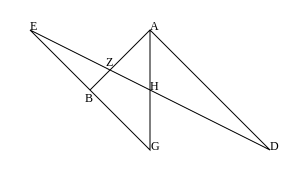
Bc ∥ Cb„Çà„Çäb = (δ/γ, 0)„Çí„ÄÅAb ∥ Ba„Çà„Çäa = (δ, 0)Âæó„Çã„ÄÇÊïÖ„Å´„ÄÅCa„ÅÆÂÇæ„Åç„ÅØ−1„Åß„ÅÇ„Çã„Åã„Çâ„ÄÅAc„Å®Âπ≥Ë°å„Åß„ÅÇ„Çã„ÄÇ ÂÝ¥Âêà2:g ∥ h„Åß„ÅÇ„ÇãÂÝ¥ÂêàÔºàÂ∞èÂÆöÁêÜÔºâ„ÄÇʨ°„ÅÆÊßò„Å´Â∫ßÊ®ô„ÇíË®≠ÂÆö„Åô„Çã„ÄÇ
Ab ∥ Ba, cB ∥ bC„Åã„Çâ„ÄÅC = (γ + 1, 1)„Å®a = (γ + 1, 0)„ÇíÂæó„Ŷ„ÄÅAc ∥ Ca„ÅåË®ºÊòé„Åï„Çå„Çã„ÄÇ Âêåʨ°Â∫ßÊ®ô„ÇíÁÅÑ„ÇãË®ºÊòéÂêåʨ°Â∫ßÊ®ôÁ≥ª„Åß„ÄÅÁÇπ„ÅÆÂ∫ßÊ®ô„Çíʨ°„ÅÆ„Çà„ÅÜ„Å´Ë®≠ÂÆö„Åô„Çã„ÄÇ
直線AC, Ac, AXの方程式をそれぞれx2 = x3, x1 = x3, x2 = x1とすれば、点B, Y, bはある数p, q, rを用いて
„Å®Êõ∏„Åë„Çã„ÄÇÁõ¥Á∑öXB, CY, cb„ÅÆÊñπÁ®ãºè„ÅØ„Åù„Çå„Åû„Çåx1 = x2p, x2 = x3q, x3 = x1r„Å®„Å™„Çã„ÄÇ„Åó„Åü„Åå„Å£„Ŷ„Åì„ÅÆ3Áõ¥Á∑ö„Åå‰∏ÄÁÇπa„Å߉∫§„Çè„Çã„Åì„Å®„ÅØrqp = 1„Å®ÂêåÂħ„Åß„ÅÇ„Çã„ÄÇ Áõ¥Á∑öCb, cB,XY„ÅÆÊñπÁ®ãºè„ÅØ„Åù„Çå„Åû„Çåx2 = x1q, x1 = x3p, x3 = x2r„Å®„Å™„Çä„Äʼn∏ÄÁÇπZ„Å߉∫§„Çè„ÇãÊù°‰ª∂„ÅØrqp = 1„Åß„ÅÇ„Çã„ÄÇÂèØÊèõ„Åß„ÅÇ„Çã„Åã„Çâpq = qp„ÄÇ„ÇÜ„Åà„Å´Cb, cB,XY„ÅÆÂÖ±ÁÇπ„ÅÆÊù°‰ª∂„Å؉ªñ„ÅÆ8Êú¨„ÅÆÁ∑ö„ÅåÂÖ±ÁÇπ„Åß„ÅÇ„Çã„Åì„Å®„Å®„Å™„Çã„ÄÇ„Åì„Çå„ÅØ„ÄÅX, Y, Z„ÅÆÂÖ±Á∑ö„Å®ÂêåÂħ„Åß„ÅÇ„Çã„ÄÇ „Åì„ÅÆË®ºÊòé„Å´„Çà„Å£„Ŷ„ÄÅ„Éë„ÉÉ„Éó„Çπ„ÅÆÂÆöÁêÜ„ÅÆÊàêÁ´ã„Å´„ÅØÂèØÊèõÊÄß„ÅåÂøÖ˶ńÅß„ÅÇ„Çã„Åì„Å®„ÅåÂàÜ„Åã„Çã[5]„ÄÇ„Éâ„ǧ„ÉÑ„ÅÆÊï∞Â≠¶ËÄÖ„ÄÅ„Ç≤„É´„Éè„É´„Éà„ɪ„Éò„ÉɄǪ„É≥„Éô„É´„ÇØ„ÅØ„Éá„Ç∂„É´„Ç∞„ÅÆÂÆöÁêÜ„ÇíÂê´„Çì„Åß„ÅÑ„Çã„Åì„Å®„ÇíÁ§∫„Åó„Åü[6][Ê≥®Èáà 2][5]„Älj∏ÄË਄Ŵ„ÄÅÂ∞ÑÂΩ±Âπ≥Èù¢„Å´„Åä„ÅфŶ„ÄÅ„Éë„ÉÉ„Éó„Çπ„ÅÆÂÆöÁêÜ„ÅÆÊàêÁ´ã„Å®ÂèØÊèõ‰Ωì„Åß„ÅÇ„Çã„Åì„Å®„ÅØÂêåÂħ„Åß„ÅÇ„Çã„ÄÇ„Éë„ÉÉ„Éó„Çπ„ÅÆÂÆöÁêÜ„ÇíÂê´„Åæ„Å™„ÅÑÂ∞ÑÂΩ±Âπ≥Èù¢„ÅØÈùûÂèØÊèõ„Å™„Éá„Ç∂„É´„Ç∞Â∞ÑÂΩ±Âπ≥Èù¢„Åß„ÄÅÈùû„Éá„Ç∂„É´„Ç∞Âπ≥Èù¢ „Åß„ÅÇ„Çã„ÄÇ Âêåʨ°Â∫ßÊ®ô„Å´„Çà„ÇãË®ºÊòé„ÅØC, c, X„ÅÆÂÖ±Á∑ö„ÅØ˵∑„Åì„Çâ„Å™„ÅÑ„Åì„Å®„ÇíÊù°‰ª∂„Å®„Åó„Ŷ„ÅÑ„Çã„ÄÇC, c, X„ÅåÂÖ±Á∑ö„Åß„ÅÇ„ÇãÂÝ¥Âêà„ÅØÂà•„ÅÆË®ºÊòé„ÇíÁÅÑ„ÇãÂøÖ˶ńÅå„ÅÇ„Çã„ÄÇ ÂèåÂØæÂ∞ÑÂΩ±Âπæ‰ΩïÂ≠¶„ÅÆÂèåÂØæÊÄß„Çà„Çä„Éë„ÉÉ„Éó„Çπ„ÅÆÂÆöÁêÜ„ÅÆÂèåÂØæ„ÇÇÊàê„ÇäÁ´ã„ŧ„ÄÇ 6Êú¨„ÅÆÁõ¥Á∑öA, b, C, a, B, c„ÅåG, H„Çí‰∏≠ÂøÉ„Å®„Åô„ÇãÊùü„ÇíÊàê„Åô„Çà„ÅÜ„Å´ÈÅ∏„Å∂„ÄÇ „ÅØÁÇπU„ÅßÂÖ±ÁÇπ„Åß„ÅÇ„Çã„ÄÇÂ∑¶„ÅÆÂõ≥„ÅØÂ∞ÑÂΩ±Âπæ‰ΩïÂ≠¶„ÄÅÂè≥„ÅÆÂõ≥„ÅØ„Ç¢„Éï„Ç£„É≥Âπæ‰ΩïÂ≠¶„Å´„Çà„ÇãË°®Áèæ„Åß„ÅÇ„Çã„ÄÇ„Ç¢„Éï„Ç£„É≥Âπæ‰ΩïÂ≠¶„ÅÆÊñπ„Åß„ÅØG, H„ÅØÁÑ°ÈôêÈÅÝÁÇπ„Åß„ÅÇ„Çã„ÄÇU„ÅåGH‰∏ä„Å´„ÅÇ„Çå„Å∞„ÄÅ„Éë„ÉÉ„Éó„Çπ„ÅÆÂÆöÁêÜ„ÅÆ"dual little theorem"„ÇíÂæó„Çã„ÄÇ „Ç¢„Éï„Ç£„É≥ÂΩ¢Âºè„ÅÆÂ∞èÂÆöÁêÜ„ÅßÂæó„ÇãÁÇπU„ÅåGH‰∏ä„Å´„ÅÇ„Çã„Äńŧ„Åæ„ÇäÁÑ°ÈôêÈÅÝÁÇπ„Åß„ÅÇ„ÇãÂÝ¥Âêà„ÄÅ„Éà„É݄Ǫ„É≥„ÅÆÂÆöÁêÜ„ÇíÂæó„Çã„ÄÇ„Éà„É݄Ǫ„É≥„ÅÆÂõ≥ÂΩ¢„ÅØÂ∞ÑÂΩ±Âπ≥Èù¢„ÅÆÂÖ¨ÁêÜ„ÅÆʱ∫ÂÆö„Ŵ§߄Åç„Å™ÂΩπÂâ≤„ÇíÊûú„Åü„Åô[7]„ÄÇ„Éà„É݄Ǫ„É≥„ÅÆÂõ≥ÂΩ¢„ÅÆÈñâÂΩ¢„ÅÆË®ºÊòé„ÅØ"little theorem"„ÅÆË®ºÊòé„Å´„Çà„ÇäË°å„Çè„Çå„Çã„ÄÇ„Åó„Åã„Åó„ÄÅʨ°„ÅÆ„Çà„ÅÜ„Å´„ÄÅ„Çà„ÇäÁ∞°Âçò„ÅßÁõ¥Êé•ÁöфřˮºÊòé„ÇÇÂ≠òÂú®„Åô„Çã„ÄÇ„Éà„É݄Ǫ„É≥„ÅÆÂÆöÁêÜ„ÅƉ∏ªÂºµ„Å´„ÅØÊé•Á∂ö„Äʼn∫§Â∑Æ„ÄÅÂπ≥Ë°å„ÅÆ„Åø„ÅåÁÅÑ„Çâ„Çå„Çã„Åü„ÇÅ„Å´„Ç¢„Éï„Ç£„É≥ÂÜôÂÉè„Å´„Çà„Å£„Ŷ‰∏ç§â„Åß„ÅÇ„Çã„Älj∏âËßíÂΩ¢„ÅÆÈÝÇÁÇπ„ÅÆÂ∫ßÊ®ô„ÇíP = (0, 0), Q = (1, 0), R = (0, 1)„Å®ÁΩÆ„Åè„ÄÇ„Åæ„ÅüÊúÄÂàù„ÅÆÁÇπ„Çí(0, λ)„Å®„Åô„Çã„ÄÇ6Âõû„ÅÆÊìç‰Ωú„ÇíÁµå„ŶÊúÄÂæå„ÅÆÁÇπ„Åå(0, λ)„Å´Ê઄Çã„Åì„Å®„ÇíË®ºÊòé„Åô„Çå„Å∞„Çà„ÅÑ„ÄÇ
パップスの定理の他の主張 パップスの定理とその双対の他の特徴づけに次の主張がある。
˵∑Ê∫ê„Åì„Çå„Çâ„ÅÆÊÄßË≥™„ÅÆÊúÄ„ÇÇÊó©„ÅÑÂΩ¢„ÅØ„Éë„ÉÉ„Éó„Çπ„ÅÆËëóÊõ∏„ÅÆVII„ÅÆÊÄßË≥™138,139,141,143„ÅßÁü•„Çâ„Çå„Ŷ„ÅÑ„Åü[Ê≥®Èáà 3]„ÄÇ„Åæ„Åü„ÄÅ„Åì„Çå„Çâ„ÅÆÊÄßË≥™„ÅØ„Ç®„Ƕ„Ç؄ɨ„ǧ„Éá„Çπ„ÅÆ Porisms „ÅÆÂ∑ªVII„ÅƉ∏ÄÈÉ®„Å´„ÅÇ„ÇãË£úÈ°åXII,XIII,XV,XVII„Åß„ÅÇ„Çã„ÄÇ „Ç®„Ƕ„Ç؄ɨ„ǧ„Éá„Çπ„ÅÆÊõ∏„Å´„ÅÇ„ÇãË£úÈ°å„Å؉ªäÊó•„Åß„ÅØ˧áÊØî„Å®„Åó„ŶÁü•„Çâ„Çå„ÇãʶÇÂøµ„ÇíÁÅфŶˮºÊòé„Åï„Çå„Ŷ„ÅÑ„Çã„ÄÇ„Åæ„Åü„ÄÅÂÖà„ÅÆ3„ŧ„ÅÆË£úÈ°å„ÇÇÂà©ÁÅï„Çå„Ŷ„ÅÑ„Çã„Älj∏ĄŧÁõÆ„ÅØË£úÈ°åIII„Åß„ÅÇ„Çã„ÄÇ („Éë„ÉÉ„Éó„Çπ„ÅÆË®òËø∞„Å®„ÅØ„ÄÅG„Å®Œì„ÄÅD„Å®Œî„ÄÅJ„Å®Œò„ÄÅL„Å®Œõ„ÅåÂØæÂøú„Åó„Ŷ„ÅÑ„Çã)„ÄÇ 3„ŧ„ÅÆÂÖ±ÁÇπÁ∑öAB, AG, AD„Åå„ÅÇ„Å£„Ŷ„ÄÅJB, JE„ÅåJ„Å߉∫§„Çè„Å£„Ŷ„ÅÑ„Çã„ÄÇ„Åæ„ÅüKL„ÅØAZ„Å®Âπ≥Ë°å„Åß„ÅÇ„Çã„ÄÇ„Åì„ÅÆ„Å®„Åç KJ : JL :: (KJ : AG & AG : JL) :: (JD : GD & BG : JB) „Åß„ÅÇ„Çã„ÄÇ„Åì„Çå„Çâ„Å؉ªäÊó•„ÄÅÁ≠âºè„Å®„Åó„Ŷʨ°„ÅÆÊßò„Å´Ë°®„Åï„Çå„Çã[Ê≥®Èáà 4]„ÄÇ KJ/JL = (KJ/AG)(AG/JL) = (JD/GD)(BG/JB) ÊúÄÂè≥Ëæ∫ (JD : GD „Å® BG : JB„ÅÆÁ©ç) „ÅØ„ÄÅÂÖ±Á∑öÁÇπJ, G, D, B„Å´ÂØæ„Åó„Ŷ˧áÊØî„Å®„Åó„ŶÁü•„Çâ„Çå„Çã„ÇÇ„ÅÆ„Åß„ÄÅ(J, G; D, B)„Å®„ÇÇÊõ∏„Åã„Çå„Çã„ÄDŽŧ„Åæ„ÇäA„Å߉∫§„Çè„Çã3Á∑ö„ÅÆ„ÅÜ„Å°„ÄÅJD„ÅÆÂèñ„ÇäÊñπ„ÅØ˧áÊØî„Å®ÁÑ°Èñ¢‰øÇ„Åß„ÅÇ„Çã„Åì„Å®„ÅåÁ§∫„Åï„Çå„Åü„ÄÇ (J, G; D, B) = (J, Z; H, E) Áõ¥Á∑öJE„ÅåA„ÇíÈÄö„Çã„Å©„ÅÆËæ∫ÔºàÁõ¥Á∑öÔºâ„Å´„ÅÇ„Åü„Çã„Åã„ÅØÈáç˶ńÅß„ÅØ„Å™„ÅÑ„ÄÇÁâπ„Å´Âõ≥„Çí§â„Åà„Çå„Å∞„Äʼnª•‰∏ã„ÅÆÊßò„Å´„Å™„Çã„Åì„Å®„ÇÇ„ÅÇ„ÇãÔºàË£úÈ°åXԺ⠄ÄÇ ÂÖàËø∞„ÅÆ„Çà„ÅÜ„Å´(J, G; D, B) = (J, Z; H, E)„Åß„ÅÇ„Çã„ÄÇ„Éë„ÉÉ„Éó„Çπ„ÅØ„Åì„Çå„ÇíË®ºÊòé„Åó„Å™„Åã„Å£„Åü„Åå„ÄŠˣúÈ°åX„ÅØ„Åì„ÅÆÊßãÂõ≥„ÅÆÈÄÜ„Äå2„ŧ„ÅÆ˧áÊØî„ÅåÁ≠â„Åó„ÅèÂõ≥„ÅÆÊßò„Å´BE, DH„ÅåA„Å߉∫§„Çè„Çã„Å®„Åô„Çå„Å∞„ÄÅÁÇπG, A, Z„ÅØÂÖ±Á∑ö„Åß„ÅÇ„Çã„Äç„ÇíË°®„Åó„Ŷ„ÅÑ„Çã„ÄÇ JK, AG„Åå‰∫§„Çè„Çâ„Å™„ÅÑÂÝ¥Âêà„ÅØ˧áÊØî„Çí (J, ‚àû; K, L) = (J, G; D, B)„ÅÆÊßò„Å´Êõ∏„Åè„Åì„Å®„Åå„Åß„Åç„Çã„ÄÇ„Éë„ÉÉ„Éó„Çπ„ÅØ„Åì„Çå„ÇíË£úÈ°åXI„ÅßÁ§∫„Åó„Ŷ„ÅÑ„Çã„ÄÇ ÂΩìÊôÇ„ÅÆË®òÊ≥ï„Åß„ÅØ DE.ZH : EZ.HD :: GB : BE„Å®„Å™„Çã„Åå„ÄÅ„Åì„Çå„ÅØ (D, Z; E, H) = (‚àû, B; E, G) „Å®„ÅÑ„ÅÜË°®Áèæ„Å´Á≠â„Åó„ÅÑ„ÄÇ Ê¨°„ÅÆÂõ≥„ÅØË£úÈ°åXII„Åß„ÅÇ„Çã„ÄÇ „Åì„ÅÆÂõ≥„ÅØË£úÈ°åXIII„Å®ÊÑèÂë≥„Åô„ÇãÊâÄ„ÅØÂêå„Åò„ÅÝ„ÅåBA, DG„ÅåËæ∫„Åƪ∂Èï∑„Å´„ÅÇ„ÇãÁÇπN„Å߉∫§„Çè„Å£„Ŷ„ÅÑ„Çã„ÄÇ„Å©„ÅÆ„Çà„ÅÜ„Å™ÂÝ¥Âêà„Åß„ÇÇ„ÄÅG„ÇíÈÄö„ÇãÁõ¥Á∑ö„ÅåA„ÇíÈÄö„ÇãÁõ¥Á∑ö„Å®‰∫§„Çè„Å£„Ŷ„ÅÑ„Çã„Å®„Åô„Çå„Å∞ („Åù„Åó„Ŷ˧áÊØî„ÅƉ∏ç§âÊÄß„ÇíÂà©ÁÅô„Çå„Å∞Ôºâ„ÄÅË£úÈ°åIII„Å®XI„Çíʨ°„ÅÆ„Çà„ÅÜ„Å´Âæó„Çã„ÄÇ (G, J; E, H) = (G, D; ‚àû, Z) D„ÇíÈÄö„ÇãÁõ¥Á∑ö„ÅåB„ÇíÈÄö„ÇãÁõ¥Á∑ö„Å®‰∫§„Çè„Å£„Ŷ„ÅÑ„Çã„Å®„Åô„Çå„Å∞„ÄÅ (L, D; E, K) = (G, D; ‚àû, Z) „ÇíÂæó„Çã„ÄÇ„Åó„Åü„Åå„Å£„Ŷ(E, H; J, G) = (E, K; D, L)„Åß„ÅÇ„Çã„ÄÇ„Åæ„ÅüË£úÈ°åX„Çà„Çä„ÄÅH, M, K„ÅØÂÖ±Á∑ö„Åß„ÅÇ„Çã„ÄÇ„Åì„Çå„ÅØ„ÄÅÂÖ≠ËßíÂΩ¢ADEGBZ„ÅƉ∏ªÂØæËßíÁ∑ö„ÅƉ∫§ÁÇπ„ÅÆÂÖ±Á∑ö„ÇíË°®„Åó„Ŷ„ÅÑ„Çã„ÄÇ Ë£úÈ°åXV„Å®XVII„ÅØ„ÄÅÁõ¥Á∑öHK, BG„ÅƉ∫§ÁÇπ„ÇíM„Å®„Åó„Ŷ„ÄÅA, M, G„ÅÆÂÖ±Á∑ö„ÇíÁ§∫„Åó„Ŷ„ÅÑ„Çã„ÄÇ„Åì„Çå„ÅØÂÖ≠ËßíÂΩ¢BEKHZG„ÅƉ∏ªÂØæËßíÁ∑ö„ÅƉ∫§ÁÇπ„ÅÆÂÖ±Á∑ö„ÇíÁ§∫„Åó„Ŷ„ÅÑ„Çã„ÄÇ ËÑöÊ≥®Ê≥®Èáà
出典
参考文献
Èñ¢ÈÄ£ÈÝÖÁõƧñÈÉ®„É™„É≥„ÇØ
|
Portal di Ensiklopedia Dunia