星型正多角形 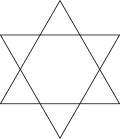 星型正多角形(ほしがたせいたかっけい、英: regular star polygon)とは、平面幾何学図形の一種で、星型多角形のうち正多角形の辺を延ばしたものでかつ、幾つかの正多角形に分解できないものを言う。 五芒星は星型正多角形であるが、六芒星は二つの正三角形に分解できるため、星型多角形ではあるが星型正多角形ではない(芒星図形に関しては星型多角形を参照)。 星型正多角形は正多角形の辺を延ばして作るほかに、正多角形の頂点を何個おきかに飛ばして結んで作ることもできる。 性質正 n 角形の内角は、「180(n - 2)/n」で求めることができる。これを星型正多角形に拡張すると、n の値は分数になり、星型五角形では、正 5/2 角形とすることができる。星型正多角形は辺の数を n、元の正多角形の頂点を結ぶときの飛び数を m として全て正 n/m 角形とすることができる(n にはもとの正多角形の角の数が入る)。また、m はこの星型正多角形が何周して元の位置に戻ったかをあらわしている。この m を星型正多角形の密度という。 1 回しか交わっていない星型偶数角形は、その偶数の半分の多角形 2 枚に分解できるため、正偶数角形から作った星型正多角形は、最低 2 回は交わっていることになる。 星型正多角形は「n と m は同じ数で割り切れない」「n > 2m」の場合のみ可能であるが、一様多面体の頂点形状をあらわすときには、ある面がほかの面と逆に交差するものはその面を n/(n - m) と表すことがある(たとえば二重三角十二・十二面体の星型五角形:[5, 5/3, 5, 5/3, 5, 5/3] など)。 関連項目外部リンク
|
Index:
pl ar de en es fr it arz nl ja pt ceb sv uk vi war zh ru af ast az bg zh-min-nan bn be ca cs cy da et el eo eu fa gl ko hi hr id he ka la lv lt hu mk ms min no nn ce uz kk ro simple sk sl sr sh fi ta tt th tg azb tr ur zh-yue hy my ace als am an hyw ban bjn map-bms ba be-tarask bcl bpy bar bs br cv nv eml hif fo fy ga gd gu hak ha hsb io ig ilo ia ie os is jv kn ht ku ckb ky mrj lb lij li lmo mai mg ml zh-classical mr xmf mzn cdo mn nap new ne frr oc mhr or as pa pnb ps pms nds crh qu sa sah sco sq scn si sd szl su sw tl shn te bug vec vo wa wuu yi yo diq bat-smg zu lad kbd ang smn ab roa-rup frp arc gn av ay bh bi bo bxr cbk-zam co za dag ary se pdc dv dsb myv ext fur gv gag inh ki glk gan guw xal haw rw kbp pam csb kw km kv koi kg gom ks gcr lo lbe ltg lez nia ln jbo lg mt mi tw mwl mdf mnw nqo fj nah na nds-nl nrm nov om pi pag pap pfl pcd krc kaa ksh rm rue sm sat sc trv stq nso sn cu so srn kab roa-tara tet tpi to chr tum tk tyv udm ug vep fiu-vro vls wo xh zea ty ak bm ch ny ee ff got iu ik kl mad cr pih ami pwn pnt dz rmy rn sg st tn ss ti din chy ts kcg ve
Portal di Ensiklopedia Dunia













