អាំងតេក្រាលកំនត់

members.dirtgame.net

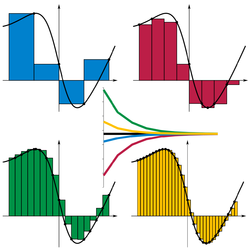
• គេមានអនុគមន៍ f(x) ដែលជាប់នៅចន្លោះ [a, b], គេចែកចន្លោះ[a, b] ជា n ផ្នែកស្មើៗគ្នាតាមលំដាប់ x₀(=a), x₁, x₂, ..., x_n(=b) និង តាង ${\displaystyle {\frac {b-a}{n}}=\bigtriangleup x}$ នោះគេបាន

• ប្រសិនបើ b=a នោះគេបាន

${\displaystyle \int _{a}^{a}f(x)\,dx\,\!=0}$

ប្រសិនបើ b < a នោះគេបាន

${\displaystyle \int _{a}^{b}f(x)\,dx\,\!=-\int _{b}^{a}f(x)\,dx}$

គេអោយអនុគមន៍ f(x) ជាអនុគមន៍កំនត់និងជាប់លើ [a, b] និង F(x) ជាព្រីមីទីវនៃអនុគមន៍ f(x)។ គេបាន ${\displaystyle \int _{a}^{b}f(x)\,dx\,\!=[F(x)]{_{a}^{b}}=F(b)-F(a)\!}$

1. គេអោយ u=u(x) និង v=v(x) ជាអនុគមន៍កំនត់និងជាប់លើចន្លោះ [a, b] នោះគេបាន ${\displaystyle \int _{a}^{b}u\,dv\,\!=[u.v]{_{a}^{b}}-\int _{a}^{b}v\,du}$

   ${\displaystyle \int _{a}^{b}f(x).g'(x)\,dx\,\!=[f(x).g(x)]{_{a}^{b}}-\int _{a}^{b}f'(x).g(x)\,dx}$

   ${\displaystyle \int _{a}^{b}f(x)\,dx\,\!=[x.f(x)]{_{a}^{b}}-\int _{a}^{b}x.f'(x)\,dx}$

ក) គណនាអាំងតេក្រាលដែលមានរាង ${\displaystyle \color {blue}I=\int _{a}^{b}{\frac {U(x)}{\ {U(x)+V(x)}}}\,dx}$

-វិធីសាស្រ្តដោះស្រាយ: គេតាង ${\displaystyle \color {Red}J=\int _{a}^{b}{\frac {V(x)}{\ {U(x)+V(x)}}}\,dx}$

គេបាន I + J = b - a និង I - J = ...? រួចគណនា I ដោយដោះស្រាយប្រព័ន្ធ ${\displaystyle {\begin{cases}I+J=b-a\\I-J=...?\end{cases}}}$

សំគាល់: គេប្រើវិធីសាស្រ្តនេះគណនាអាំងតេក្រាលដែលមានរាង

${\displaystyle \color {blue}I=\int _{a}^{b}{\frac {U(sinx)}{\ {U(sinx)+U(cosx)}}}\,dx}$    និង ${\displaystyle \color {blue}J=\int _{a}^{b}{\frac {U(cosx)}{\ {U(sinx)+U(cosx)}}}\,dx}$ ដែល ${\displaystyle a+b={\frac {\pi }{2}}}$

រឺ ${\displaystyle \color {blue}I=\int _{a}^{b}{\frac {U(tanx)}{\ {U(tanx)+U(cotx)}}}\,dx}$    និង ${\displaystyle \color {blue}J=\int _{a}^{b}{\frac {U(cotx)}{\ {U(tanx)+U(cotx)}}}\,dx}$ ដែល ${\displaystyle a+b={\frac {\pi }{2}}}$

-វិធីសាស្រ្តដោះស្រាយ: គេតាង ${\displaystyle t={\frac {\pi }{2}}-x}$ រួចគណនា I, J ដោយដោះស្រាយប្រព័ន្ធសមីការ ${\displaystyle {\begin{cases}I+J=b-a\\I=J\end{cases}}}$

ខ) គេអោយ f ជាអនុគមន៍កំនត់និងជាប់លើ [-a, a]។ គេតាង ${\displaystyle \color {Red}I=\int _{-a}^{a}f(x)\,dx}$

1. បង្ហាញថាបើ f ជាអនុគមន៍គូលើ [-a, a] នោះគេបាន ${\displaystyle I=2\int _{0}^{a}f(x)\,dx}$
2. បង្ហាញថាបើ f ជាអនុគមន៍សេសលើ [-a, a] នោះគេបាន I = 0

-វិធីសាស្រ្តដោះស្រាយ: គេមាន ${\displaystyle \color {blue}I=\int _{-a}^{0}f(x)\,dx+\int _{0}^{a}f(x)\,dx}$

ចំពោះ${\displaystyle \color {blue}\int _{-a}^{0}f(x)\,dx}$ គេតាង ${\displaystyle t=-x}$

គ) គេអោយ f ជាអនុគមន៍កំនត់និងជាប់លើ [a, b]។ គេបាន ${\displaystyle \color {blue}\int _{a}^{b}f(x)\,dx=\int _{a}^{b}f(a+b-x)\,dx}$

-វិធីសាស្រ្តដោះស្រាយ: គេតាង ${\displaystyle t=a+b-x}$

សំគាល់: គេច្រើនប្រើវិធីសាស្រ្តនេះដើម្បីគណនាអាំងតេក្រាលនៃអនុគមន៍ត្រីកោណមាត្រដែល:

${\displaystyle a+b=\pi }$ រឺ ${\displaystyle a+b={\frac {\pi }{2}}}$ រឺ ${\displaystyle a+b={\frac {\pi }{4}}}$

ឃ) គេអោយ f ជាអនុគមន៍ជាប់ និងជាអនុគមន៍ខួបមានខួប T។ បង្ហាញថា ${\displaystyle \color {blue}\int _{a}^{a+T}f(x)\,dx=\int _{a-T}^{a}f(x)\,dx}$

-វិធីសាស្រ្តដោះស្រាយ: គេតាង t = x - T

ង) គេអោយ f ជាអនុគមន៍កំនត់និងជាប់។ បង្ហាញថា: ${\displaystyle \color {blue}\int _{a}^{2a}f(x)\,dx=\int _{0}^{a}[f(x)+f(2a-x)]\,dx}$

-វិធីសាស្រ្តដោះស្រាយ: គេមាន ${\displaystyle \int _{a}^{2a}f(x)\,dx=\int _{0}^{a}f(x)\,dx+\int _{a}^{2a}f(x)\,dx}$

ចំពោះ ${\displaystyle \int _{a}^{2a}f(x)\,dx}$ គេតាង t = 2a - x

ច) គេអោយ f ជាអនុគមន៍កំនត់និងជាប់ហើយផ្ទៀងផ្ទាត់លក្ខខណ្ឌ f(a+b-x) = f(x)ដែល a, b ជាចំនួនគេស្គាល់ជាមុន។ បង្ហាញថា ${\displaystyle \int _{a}^{b}xf(x)\,dx={\frac {a+b}{2}}\int _{a}^{b}f(x)\,dx}$

-វិធីសាស្រ្តដោះស្រាយ: គេតាង t = a + b -x

ឆ) គេអោយ b ជាចំនួនពិតវិជ្ជមាន និង f ជាអនុគមន៍ជាប់និងជាអនុគមន៍គូលើ[-a, a]។ បង្ហាញថា ${\displaystyle \int _{-a}^{a}{\frac {f(x)}{b^{x}+1}}\,dx=\int _{0}^{a}f(x)\,dx}$

-វិធីសាស្រ្តដោះស្រាយ: គេមាន ${\displaystyle \int _{-a}^{a}{\frac {f(x)}{b^{x}+1}}\,dx=\int _{-a}^{0}{\frac {f(x)}{b^{x}+1}}\,dx+\int _{0}^{a}{\frac {f(x)}{b^{x}+1}}\,dx}$

ចំពោះ ${\displaystyle \int _{-a}^{0}{\frac {f(x)}{b^{x}+1}}\,dx}$ គេតាង t = -x

សំរាយបញ្ជាក់

1. តាង ${\displaystyle x={\frac {\pi }{2}}-t,\quad {\frac {dx}{dt}}=-1}$ នោះគេបាន ${\displaystyle t={\frac {\pi }{2}}}$ នៅពេល ${\displaystyle x=0\,}$ និង ${\displaystyle t=0\,}$ នៅពេល ${\displaystyle x={\frac {\pi }{2}}}$

${\displaystyle \therefore \int _{0}^{\frac {\pi }{2}}\sin ^{n}dx=\int _{\frac {\pi }{2}}^{0}\sin ^{n}({\frac {\pi }{2}}-t)(-1)dt=\int _{0}^{\frac {\pi }{2}}\sin ^{n}({\frac {\pi }{2}}-t)dt=\int _{0}^{\frac {\pi }{2}}\cos ^{n}tdt=\int _{0}^{\frac {\pi }{2}}\cos ^{n}xdx}$

2. តាង ${\displaystyle I_{n}=\int _{0}^{\frac {\pi }{2}}\sin ^{n}xdx\quad }$ ចំពោះ ${\displaystyle n\geq 2\quad }$ គេបាន

${\displaystyle {\begin{aligned}I_{n}&=\int _{0}^{\frac {\pi }{2}}\sin ^{n-1}x(-\cos x)'dx=[\sin ^{n-1}x(-\cos x)]_{0}^{\frac {\pi }{2}}+(n-1)\int _{0}^{\frac {\pi }{2}}\sin ^{n-2}x\cdot \cos ^{2}xdx\\&=(n-1)\int _{0}^{\frac {\pi }{2}}\sin ^{n-2}x(1-\sin ^{2}x)dx=(n-1)I_{n-2}-(n-1)I_{n}\end{aligned}}}$

${\displaystyle \therefore nI_{n}=(n-1)I_{n-2}\qquad \Rightarrow I_{n}={\frac {n-1}{n}}\cdot I_{n-2}\qquad \circledast }$

គេបាន ${\displaystyle I_{1}=\int _{0}^{\frac {\pi }{2}}\sin xdx=-[\cos x]_{0}^{\frac {\pi }{2}}=1,\quad I_{0}=\int _{0}^{\frac {\pi }{2}}dx={\frac {\pi }{2}}}$

ដូចនេះគេបាន${\displaystyle \circledast \qquad }$ កំនត់ដោយ

• ប្រសិនបើ n ជាចំនួនគូ គេបាន       ${\displaystyle I_{n}={\frac {n-1}{n}}\cdot {\frac {n-3}{n-2}}\cdots \cdots {\frac {3}{4}}\cdot {\frac {1}{2}}\cdot {\frac {\pi }{2}}}$
• ប្រសិនបើ n ជាចំនួនសេស គេបាន ${\displaystyle I_{n}={\frac {n-1}{n}}\cdot {\frac {n-3}{n-2}}\cdots \cdots {\frac {2}{3}}\cdot 1}$

ឧទាហរណ៍៖ ${\displaystyle \int _{0}^{\frac {\pi }{2}}\sin ^{5}xdx={\frac {4}{5}}\cdot {\frac {2}{3}}={\frac {8}{15}},\qquad \int _{0}^{\frac {\pi }{2}}\cos ^{4}xdx=\int _{0}^{\frac {\pi }{2}}\sin ^{4}xdx={\frac {3}{4}}\cdot {\frac {1}{2}}\cdot {\frac {\pi }{2}}={\frac {3}{16}}\pi }$

• អាំងតេក្រាលមិនកំនត់
• អាំងតេក្រាលឌុប
• អាំងតេក្រាលត្រីគុណ
• អាំងតេក្រាលខ្សែកោង
• អាំងតេក្រាលផ្ទៃ