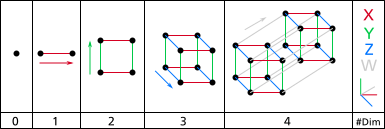정팔포체

이 문서는 다른 언어판 위키백과의 문서(en:Tesseract)를 번역 중이며, 한국어로 좀 더 다듬어져야 합니다. 번역에 이상이 있다면 직접 편집하시거나, 해당 글의 토론 문서에 의견을 남겨주세요.

정팔포체
슈레겔 다이어그램의 모습.
종류	4차원 볼록 정다포체
슐레플리 기호	{4, 3, 3} t0, 3{4, 3, 2} 또는 {4, 3}×{ } t0, 2{4, 2, 4} 또는 {4}×{4} t0, 2, 3{4, 2, 2} 또는 {4}×{ }×{ } t0, 1, 2, 3{2, 2, 2} 또는 { }×{ }×{ }×{ }
콕서터 다이어그램
포	8개 (4.4.4)
면	24개 {4}
모서리	32개
꼭짓점	16개
꼭짓점 그림	사면체
페트리 다각형	팔각형
쌍대	정십육포체
속성	볼록, 점추이, 변추이, 면추이
유니폼 색인	10

정팔포체 또는 4차원 초입방체(영어: Tesseract)는 8개의 정육면체로 이루어진 4차원의 정다포체이다.

정육면체 철사를 비눗물에 2번 담가서 비눗방울을 만들 때 일종의 정팔포체의 투영의 형태가 되는 것으로 알려져 있다. (단, 이때 면은 약간 비뚤어진다.)^[1]

기하학적으로 보았을 때 정팔포체는 정육면체의 4차원 아날로그라고 할 수 있다. 정육면체의 표면이 6개의 정사각형 모양의 면으로 구성되어 있는 것처럼 정팔포체의 초표면(hypersurface)은 8개의 정육면체 모양의 포로 구성되어 있는 것이다. 정팔포체는 6개의 4차원 볼록 정다포체 중 하나이다.

정팔포체의 영어 표기는 일반적으로 tesseract이며 그 외에도 8-cell, C₈, octachoron, octahedroid^[2], cubic prism, tetracube^{[주 1]}라고도 불린다. 이것은 4차원 초입방체(영어: four-dimensional hypercube) 또는 초입방체의 차원 계열의 일부인 4-정육면체(영어: 4-cube) 또는 "측정 폴리토프"이다.^[3]

옥스포드 영어사전(영어: Oxford English Dictionary)에 따르면 1888년 찰스 하워드 힌톤이 그의 저서 《생각의 새로운 시대》(영어: A New Era of Thought)에서 고대 그리스어의 τέσσερεις ακτίνες(téssereis aktines, 4개의 광선)에서 단어를 따와 최초로 tesseract라는 단어를 사용했다고 한다(정팔포체가 한 꼭짓점에서 다른 꼭짓점까지 총 4개의 변이 있다는 성질을 이용한 것이다).^[4] 그러나 이 간행물과 힌튼의 후기 저작물에서는 이 단어는 간혹 tessaract라고 쓰이기도 했다.

정팔포체는 여러 방법으로 만들 수 있다. 정팔포체는 모든 모서리 주위에 함께 접혀진 3개의 정육면체를 가진 정다포체로서 그것은 384개의 사면체 대칭을 가진 슐레플리 기호 {4, 3, 3}을 가지고 있다. 두 개의 평행 정육면체로 구성된 4D 하이프리즘으로 제작되었으며 대칭성 순서 96을 갖는 합성 슐레플리 기호인 {4, 3} × { }로 명명될 수 있다. 그리고 대칭성 순서 64를 갖는 4-4 듀오프리즘일 때 2개의 사각형이 곱집합되며 이것은 합성 슐레플리 기호인 {4}×{4}로 명명될 수 있다. 그리고 대칭성 순서 16을 갖는 하이퍼래탱글로써 그것은 합성 슐레플리 기호인 { } × { } × { } × { } 또는 { }⁴로 명명될 수 있다.

정팔포체의 각 꼭짓점은 4개의 모서리에 인접하므로 정팔포체의 정점도는 사면체이다. 정팔포체의 이중 폴리토프는 슐레플리 기호 {3,3,4}를 가지고 있는 정십육포체(영어: hexadecachoron 또는 16-cell)이다.

유클리드 4 공간의 표준인 정팔포체는 점(±1, ±1, ±1, ±1)의 볼록한 선체로 주어진다. 즉 아래와 같은 점으로 구성된다:

${\displaystyle \{(x_{1},x_{2},x_{3},x_{4})\in \mathbb {R} ^{4}\,:\,-1\leq x_{i}\leq 1\}}$

정팔포체는 8개의 초평면으로 제한된다(x_i = ±1). 비평행형 초평면의 각 쌍은 교차하여 정팔포체에서 정사각형 모양의 면 24개를 형성한다. 3개의 정육면체와 3개의 사각형이 각 모서리에서 교차한다. 모든 정점에서 4개의 정육면체, 6개의 정사각형 및 4개의 모서리가 있는 것이다. 모두 8개의 정육면체, 24개의 사각형, 32개의 모서리, 16개의 꼭짓점으로 구성되는 것이다.

초입방체의 구성은 아래와 같이 생각할 수 있다:

• 1차원 : 2개의 점 A와 점 B를 선으로 연결하여 선분 AB를 만든다.
• 2차원 : 2개의 평행한 선분 AB와 선분 CD를 연결하여 정사각형 ABCD를 만든다.
• 3차원 : 2개의 평행한 정사각형 ABCD와 정사각형 EFGH를 연결하여 정육면체 ABCDEFGH를 만든다.
• 4차원 : 2개의 평행한 정육면체 ABCDEFGH와 IJKLMNOP를 연결하여 초입방체 ABCDEFGHIJKLMNOP를 만든다.

정육면체를 2차원 투영할 수 있듯이 정팔포체도 2, 3차원 투영이 가능하다.

2D 평면상에 투영된 꼭짓점들의 위치를 재배치함으로써 더 유익해진다. 이러한 방식으로 더 이상 정팔포체 내의 공간 관계를 반영하지 않는, 아래 예재와 같이 꼭짓점의 연결 구조를 나타내는 그림을 얻어낼 수 있다:

정팔포체는 원칙적으로 2개의 정육면체를 결합하여 얻는다. 이 원칙은 2개의 정사각형으로 이루어진 구조의 정육면체와 비슷하며 하위 차원인 정육면체의 두 복사본을 병치하고 해당 꼭짓점을 연결한다는 것이다. 정팔포체의 각 모서리는 길이가 같다. 이것은 네트워크 토폴로지가 여러 프로세서를 병렬 컴퓨팅으로 연결하기 위한 기초로 정팔포체를 사용할 때 중요하다. 두 노드 사이의 거리는 최대 4이고 무게 균형을 허용하는 많은 경로가 있다.

정팔포체의 3차원 공간으로의 첫 번째 포의 평행 투영은 정육면체 모양의 엔벨로프를 갖는다. 가장 가까운 포와 가장 먼 포가 정육면체로 투영되고 나머지 6개의 포가 6개의 정사각형 모양의 면에 투영된다. 정팔포체의 3차원 공간으로의 첫 번째 면의 평행 투영은 직육면체 모양의 엔벨로프를 갖는다. 이 엔벨로프의 상반부와 하반부에 2쌍의 포가 돌출되어 있으며 나머지 4개의 포는 측면에 투사된다. 정팔포체의 3차원 공간으로의 첫 번째 모서리의 평행 투영은 육각기둥 모양의 엔벨로프를 갖는다. 6개의 포는 3차원 입방체의 면이 육각형 엔벨로프로 6개의 마름모에 투영되는 것과 유사한 방식으로 육각기둥에 배치된 마름모꼴 프리즘에 투영되고, 나머지 2개의 포는 각기둥의 밑면에 투영된다.

• 
• 
• 
• 
  정팔포체의 회전도
• 
• 
  왼쪽의 그림을 평행법으로 입체적으로 볼 수 있다.
• 

• 정십육포체
• 정이십사포체
• 정백이십포체
• 정육백포체

• (한국어) 네이버 캐스트 - 4차원 입체도형
• (일본어) 삼각 사각의 비눗방울?