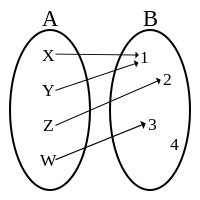
Сурјективна функција

Сурјекција. До секој елемент во кодоменот B има стрелка од (барем еден) елемент од доменот А

Во математиката, сурјективна функција е функција f : A → B ако секој елемент во B е слика на барем еден елемент од A, односно за секој елемент b од кодоменот B постои барем еден елемент a од доменот А таков што f(a)=b, т.е. кодоменот и сликата на f е истото множество.^[1][2]

Терминот сурјективност и сродните термини инјективност и бијективност беа воведени од страна на Никола Бурбаки (Nicholas Bourbaki)^[3] (и група други, главно француски, математичари од 20 век) кој, почнувајќи од 1935 година, напиша серија книги за презентирање на модерната напредна математика. Француската претставка сур значи над или одозгора и се однесува на фактот дека сликата на доменот на сурјективна функција целосно го покрива кодоменот на функцијата.

Не е сурјекција. Постои елемент во кодоменот В без стрелка од елемент во доменот А

Формално имаме:

${\displaystyle f:A\rightarrow B}$  е сурјективна функција ако  ${\displaystyle \forall b\in B\,\,\exists a\in A}$  таков што  ${\displaystyle f(a)=b\,.}$

Елементот ${\displaystyle b}$ се вика слика на елементот ${\displaystyle a}$.

• Формалната дефиниција значи: Секој елемент од кодоменот B е слика на барем еден елемент од доменот A.

Елементот ${\displaystyle a}$ се вика претслика на елементот ${\displaystyle b}$.

• Формалната дефиниција значи: Секој елемент од кодоменот B има барем една претслика во доменот A.

Претслика на сурјекција не мора да биде единствена. Во првата слика, и {X} и {Y} се претслики на елементот {1}. Baжно е да има барем една претслика. (Види и: Инјективна функција, Бијективна функција)

Нека f(x):ℝ→ℝ е реална функција y од реален аргумент x. (Значи влез и излез се броеви.)

• Графичко толкување: функцијата f е сурјективна ако секоја хоризонтала права го пресекува графиконот на f во (барем) една точка.
• Алгебарско толкување: функцијата f е сурјективна ако за кој било реален број y_o може да се најде (барем еден) реален број x_o таков што y_o=f(x_o).

Од сето ова следува дека формално докажување на сурјективност не е едноставно и тоа треба да се земе во обѕир во дискусиите подолу.

Пример: Линеарната функција на која било коса права е сурјективна, односно y=ax+b каде што a≠0 е сурјекција (и инјекција, така што е бијекција). (Види линеарна функција.)

Доказ: Заменувајќи кој било реален број y_o во функцијата и решавајќи за x, се добива x= (y_o-b)/_a така што x_o=(y_o-b)/_a. Со ова се докажа сурјективноста на функцијата y=ax+b каде што a≠0. (Бидејќи има точно едно решение за секој y_o, оваа функција е и инјективна.)

Практичен пример: y= –2x+4. Кој е претслика на y=2? Тука a=–2, т.е. a≠0 и прашањето е: за кој x e y=2? Заменувајќи y=2 во функцијата се добива x=1, т.е. y(1)=2.

Пример: Функцијата f(x)=x³–3x е сурјективна.

Дискусија: Кубна полиномна равенка x³-3x-y_o=0 има реални коефициенти (a₃=1, a₂=0, a₁=–3, a₀=–y_o), а секоја кубна полиномна равенка има барем еден реален корен.^[4] Бидејќи доменот на функцијата е ℝ, следува дека постои (барем еден) x_o таков што (x₀)³-3x₀-y_o=0 и функцијата е сурјективна. (Меѓутоа, оваа функција не е инјективна. На пример, y_o=2 има две претслики: x=–1 и x=2 , а всушност за секој y, –2≤y≤2 функцијата има повеќе од една претслика, т.е. повеќе од еден x таков што f(x)=y.)

Пример: Квадратната функција f(x) = x² не е сурјективна. Нема x таков што x² = −1. Сликата на x² e [0,+∞) , т.е. множеството на ненегативни броеви. (Оваа функција не е ниту инјективна.)

Забелешка: Се разбира дека за секоја несурјективна функција можеме да дефинираме нова сурјективна функција ограничувајќи го кодоменот на сликата. На пример „новата функција“ f_N(x):ℝ→[0,+∞) каде што f_N(x) = x² сега е сурјективна функција. (Ова не е исто со рестрикција на функција во која се ограничува доменот!)

Пример: Експоненцијалната функција f(x) = 10^x не е сурјективна. Сликата на 10^x е (0,+∞), a (0,+∞)≠ℝ. (Оваа функција е инјективна.)

Сурјекција. f(x):ℝ→ℝ (и инјекција)	Сурјекција. f(x):ℝ→ℝ (не е инјекција)	Не е сурјекција. f(x):ℝ→ℝ (не е инјекција)
Не е сурјекција. f(x):ℝ→ℝ (е инјекција)	Сурјекција. f(x):(0,+∞)→ℝ (и инјекција)	Сурјекција. z:ℝ²→ℝ, z=y. (Во сликата се показжува дека претсликата на z=2 е правата y=2.)

Пример: Инверзната функција на 10^x, односно логаритамската функција со основа 10 f(x):(0,+∞)→ℝ дефиниранa со f(x)=log(x) односно y=log(x) е сурјективна (и инјективна).

• Проекцијата на Декартов производ A × B на еден од неговите фактори е сурјективна функција.

Пример: Функцијата f((x,y)):ℝ²→ℝ дефинирана со z=y е сурјективна. Графиконот е рамнина во 3-димензионален простор, а претслика на z_o е правата y=z_o во x0y рамнината.

• Во 3-димензионални игри, вектори се проектираат на 2-димензионален екран со сурјективна функција.

• Функција
• Инјективна функција
• Бијективна функција

• „Injective, Surjective, Bijective“ (англиски). 2013. Посетено на 1 декември 2013. интерактивен квиз
• „Injectivity, Surjectivity“ (англиски). Wolfram Alpha. Архивирано од изворникот на 2013-11-25. Посетено на 1 декември 2013. интерактивно