–ò–Ω—ò–µ–∫—Ç–∏–≤–Ω–∞ —Ñ—É–Ω–∫—Ü–∏—ò–∞
–í–æ –º–∞—Ç–µ–º–∞—Ç–∏–∫–∞—Ç–∞, –∏–Ω—ò–µ–∫—Ç–∏–≤–Ω–∞ —Ñ—É–Ω–∫—Ü–∏—ò–∞ –µ —Ñ—É–Ω–∫—Ü–∏—ò–∞ f : A ‚Üí B –∞–∫–æ —Ä–∞–∑–ª–∏—á–Ω–∏ –µ–ª–µ–º–µ–Ω—Ç–∏ –æ–¥ A —Å–µ –ø—Ä–µ—Å–ª–∏–∫—É–≤–∞–∞—Ç –≤–æ —Ä–∞–∑–ª–∏—á–Ω–∏ –µ–ª–µ–º–µ–Ω—Ç–∏ –æ–¥ B, –æ–¥–Ω–æ—Å–Ω–æ –∑–∞ —Å–µ–∫–æ—ò –µ–ª–µ–º–µ–Ω—Ç b –æ–¥ –∫–æ–¥–æ–º–µ–Ω–æ—Ç B –ø–æ—Å—Ç–æ–∏ –Ω–∞—ò–º–Ω–æ–≥—É –µ–¥–µ–Ω –µ–ª–µ–º–µ–Ω—Ç a –æ–¥ –¥–æ–º–µ–Ω–æ—Ç –ê —Ç–∞–∫–æ–≤ —à—Ç–æ f(a)=b.[1][2] –¢–µ—Ä–º–∏–Ω–æ—Ç –∏–Ω—ò–µ–∫—Ç–∏–≤–Ω–æ—Å—Ç –∏ —Å—Ä–æ–¥–Ω–∏—Ç–µ —Ç–µ—Ä–º–∏–Ω–∏ —Å–∏—Ä—ò–µ–∫—Ç–∏–≤–Ω–æ—Å—Ç –∏ –±–∏—ò–µ–∫—Ç–∏–≤–Ω–æ—Å—Ç –±–µ–∞ –≤–æ–≤–µ–¥–µ–Ω–∏ –æ–¥ —Å—Ç—Ä–∞–Ω–∞ –Ω–∞ –ù–∏–∫–æ–ª–∞ –ë—É—Ä–±–∞–∫–∏ (Nicholas Bourbaki)[3] (–∏ –≥—Ä—É–ø–∞ –¥—Ä—É–≥–∏, –≥–ª–∞–≤–Ω–æ —Ñ—Ä–∞–Ω—Ü—É—Å–∫–∏ –º–∞—Ç–µ–º–∞—Ç–∏—á–∞—Ä–∏ –æ–¥ 20 –≤–µ–∫) –∫–æ—ò –ø–æ—á–Ω—É–≤–∞—ò—ú–∏ –æ–¥ 1935 –≥–æ–¥–∏–Ω–∞ –Ω–∞–ø–∏—à–∞ —Å–µ—Ä–∏—ò–∞ –∫–Ω–∏–≥–∏ –∑–∞ –ø—Ä–µ–∑–µ–Ω—Ç–∏—Ä–∞—ö–µ –Ω–∞ –º–æ–¥–µ—Ä–Ω–∞—Ç–∞ –Ω–∞–ø—Ä–µ–¥–Ω–∞ –º–∞—Ç–µ–º–∞—Ç–∏–∫–∞.
–û—Å–Ω–æ–≤–Ω–∏ —Å–≤–æ—ò—Å—Ç–≤–∞–§–æ—Ä–º–∞–ª–Ω–æ –∏–º–∞–º–µ:
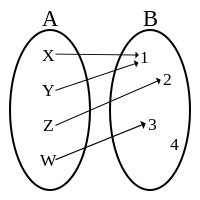
–ï–ª–µ–º–µ–Ω—Ç–æ—Ç —Å–µ –≤–∏–∫–∞ –ø—Ä–µ—Ç—Å–ª–∏–∫–∞ –Ω–∞ –µ–ª–µ–º–µ–Ω—Ç–æ—Ç . –ü—Ä–µ—Ç—Å–ª–∏–∫–∞ –Ω–∞ —Å–µ–∫–æ—ò –µ–ª–µ–º–µ–Ω—Ç –≤–æ –∫–æ–¥–æ–º–µ–Ω–æ—Ç –Ω–∞ –µ–¥–Ω–∞ –∏–Ω—ò–µ–∫—Ü–∏—ò–∞ –Ω–µ –º–æ—Ä–∞ –¥–∞ –ø–æ—Å—Ç–æ–∏. –í–æ –ø—Ä–≤–∞—Ç–∞ —Å–ª–∏–∫–∞, –µ–ª–µ–º–µ–Ω—Ç–æ—Ç {4} –Ω–µ–º–∞ –ø—Ä–µ—Ç—Å–ª–∏–∫–∞. Ba–∂–Ω–æ –µ –¥–∞ –∏–º–∞ –º–∞–∫—Å–∏–º—É–º –µ–¥–Ω–∞ –ø—Ä–µ—Ç—Å–ª–∏–∫–∞. (–í–∏–¥–∏ –∏: –°—É—Ä—ò–µ–∫—Ç–∏–≤–Ω–∞ —Ñ—É–Ω–∫—Ü–∏—ò–∞, –ë–∏—ò–µ–∫—Ç–∏–≤–Ω–∞ —Ñ—É–Ω–∫—Ü–∏—ò–∞)
–ö–∞—Ä–¥–∏–Ω–∞–ª–Ω–æ—Å—Ç–ö–∞—Ä–¥–∏–Ω–∞–ª–Ω–æ—Å—Ç–∞ –Ω–∞ –µ–¥–Ω–æ –º–Ω–æ–∂–µ—Å—Ç–≤–æ –µ –º–µ—Ä–∫–∞ –Ω–∞ –±—Ä–æ—ò–æ—Ç –Ω–∞ –µ–ª–µ–º–µ–Ω—Ç–∏—Ç–µ –≤–æ –º–Ω–æ–∂–µ—Å—Ç–≤–æ—Ç–æ. –ù–∞ –ø—Ä–∏–º–µ—Ä, –∞–∫–æ A={X,Y,Z,W}, —Ç–æ–≥–∞—à –∫–∞—Ä–¥–∏–Ω–∞–ª–Ω–æ—Å—Ç–∞ –Ω–∞ –ê –µ 4 –∏ –ø–∏—à—É–≤–∞–º–µ #A=4.[4]
–ü—Ä–∏–º–µ—Ä–∏–ï–ª–µ–º–µ–Ω—Ç–∞—Ä–Ω–∏ —Ñ—É–Ω–∫—Ü–∏–∏–ù–µ–∫–∞ f(x):‚Ñù‚Üí‚Ñù –µ —Ä–µ–∞–ª–Ω–∞ —Ñ—É–Ω–∫—Ü–∏—ò–∞ y –æ–¥ —Ä–µ–∞–ª–µ–Ω –∞—Ä–≥—É–º–µ–Ω—Ç x. (–ó–Ω–∞—á–∏ –≤–ª–µ–∑ –∏ –∏–∑–ª–µ–∑ —Å–µ –±—Ä–æ–µ–≤–∏.)
–ü—Ä–∏–º–µ—Ä: –õ–∏–Ω–µ–∞—Ä–Ω–∞—Ç–∞ —Ñ—É–Ω–∫—Ü–∏—ò–∞ –Ω–∞ –∫–æ—ò–∞ –±–∏–ª–æ –∫–æ—Å–∞ –ø—Ä–∞–≤–∞ –µ –∏–Ω—ò–µ–∫—Ç–∏–≤–Ω–∞, –æ–¥–Ω–æ—Å–Ω–æ y=ax+b –∫–∞–¥–µ —à—Ç–æ a‚âÝ0 –µ –∏–Ω—ò–µ–∫—Ü–∏—ò–∞ (–∏ —Å—É—Ä—ò–µ–∫—Ü–∏—ò–∞, —Ç–∞–∫–∞ —à—Ç–æ –µ –±–∏—ò–µ–∫—Ü–∏—ò–∞). (–í–∏–¥–∏ –ª–∏–Ω–µ–∞—Ä–Ω–∞ —Ñ—É–Ω–∫—Ü–∏—ò–∞.)
Пример: Кубната полиномна функција f(x)=x3 е инјективна. Меѓутоа, кубната полиномна функција f(x)=x3 –3x не е инјективна.
f(x)=x3 —Ç–æ—á–Ω–æ –µ–¥–Ω–∞—à. (–û–≤–∞–∞ —Ñ—É–Ω–∫—Ü–∏—ò–∞ –µ –∏ —Å—É—Ä—ò–µ–∫—Ç–∏–≤–Ω–∞.)
f(x)=x3 –3x има повеќе од една претслика, т.е. повеќе од еден x таков што f(x)=y.) Пример: Квадратната функција f(x) = x2 не е инјективна. Двата броеви x=2 и x=-2 се пресликуваат во {4} со што е докажано дека оваа функција не е инјективна. (Оваа функција не е ниту сурјективна.) Забелешка: Со ограничување на доменот, честопати можеме да дефинираме нова функција која е инјективна. На пример, со ограничување на доменот на квадратната функција имаме „нова“ функција, f/[0,+∞)(x):[0,+∞) → ℝ каде што f/[0,+∞)(x) = x2 која сега е инјективна функција. Оваа функција се вика рестрикцијата на f до [0,+∞). Пример: Експоненцијалната функција f(x) = 10x е инјективна. (Оваа функција не е сурјективна.) Дискусија: Која било хоризонтална права над х-оската го пресекува графиконот на 10x точно еднаш, а останатите хоризонтални прави не го сечат графиконот ниту еднаш. Забелешка: Инјективноста на експоненцијална функција може да се користи на следниот начин:
–î—Ä—É–≥–∏ –ø—Ä–∏–º–µ—Ä–∏ —Å–æ —Ä–µ–∞–ª–Ω–∏ —Ñ—É–Ω–∫—Ü–∏–∏–ü—Ä–∏–º–µ—Ä: –ò–Ω–≤–µ—Ä–∑–Ω–∞—Ç–∞ —Ñ—É–Ω–∫—Ü–∏—ò–∞ –Ω–∞ 10x, –æ–¥–Ω–æ—Å–Ω–æ –ª–æ–≥–∞—Ä–∏—Ç–∞–º—Å–∫–∞—Ç–∞ —Ñ—É–Ω–∫—Ü–∏—ò–∞ —Å–æ –æ—Å–Ω–æ–≤–∞ 10, f(x):(0,+‚àû)‚Üí‚Ñù –¥–µ—Ñ–∏–Ω–∏—Ä–∞–Ωa —Å–æ f(x)=log(x) –æ–¥–Ω–æ—Å–Ω–æ y=log(x) –µ –∏–Ω—ò–µ–∫—Ç–∏–≤–Ω–∞ (–∏ —Å—É—Ä—ò–µ–∫—Ç–∏–≤–Ω–∞).
–ù–∞–≤–æ–¥–∏
–ü–æ–≤—Ä–∑–∞–Ω–æ–ù–∞–¥–≤–æ—Ä–µ—à–Ω–∏ –≤—Ä—Å–∫–∏
|
Portal di Ensiklopedia Dunia