പോയിൻകാരെ കൺജെക്ചർ 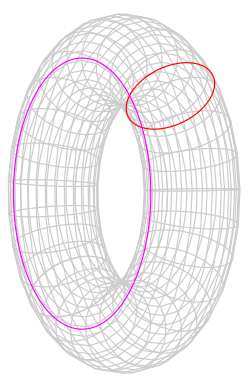 ഗണിതത്തിൽ പോയിൻകാരെ കൺജെക്ചർ (/ˌpwæ̃kɑːˈreɪ//ˌpwæ̃kɑːˈreɪ/; French: [pwɛ̃kaʁe]) 3-സ്ഫിയറുകളുടെ ആകൃതിയെ സംബന്ധിയ്ക്കുന്ന ഒരു പ്രമേയമാണ്. മൂന്ന് മാനങ്ങളുള്ള ഇടത്തിൽ ഒരു ത്രിമാന ഗോളത്തിന്റെ ഉപരിതലം ദ്വിമാനം ആണല്ലോ. ടോപ്പോളജിയിൽ ഇതിനെ 2-സ്ഫിയർ എന്ന് വിളിയ്ക്കുന്നു. അതുപോലെ നാലു മാനങ്ങളുള്ള ഒരു ഇടത്തിലെ നാലു മാനങ്ങളുള്ള ഒരു ഗോളത്തിന്റെ (ഹൈപ്പർസ്ഫിയർ) ഉപരിതലമാണ് 3-സ്ഫിയർ. ഈ കൺജെക്ചർ കൃത്യമായി താഴെ കൊടുത്തിരിയ്ക്കുന്നു:
പശ്ചാത്തലംഫ്രഞ്ച് ഗണിതശാസ്ത്രജ്ഞനായ ഹെൻറി പോയിൻകാരെ ആണ് ഈ കൺജെക്ചർ ആദ്യം പ്രസ്താവിച്ചത്. ഇത് സാധാരണ മൂന്ന് മാനങ്ങളുള്ള ഇടത്തിന് സമാനമായതും, കണ്ണെക്ടഡും, പരിമേയവും എന്നാൽ അതിരുകൾ ഇല്ലാത്തതുമായ ഒരു ഇടത്തിനെ (ക്ലോസ്ഡ് 3-മാനിഫോൾഡ്) ബാധിയ്ക്കുന്ന പ്രമേയമാണ്. അദ്ദേഹത്തിന്റെ കൺജെക്ചർ പ്രകാരം ഇത്തരം ഒരു ഇടത്തിന് അതിലെ ഏതൊരു വലയവും (loop) ഒരു ബിന്ദുവിലേയ്ക്ക് വലിച്ചു ചുരുക്കാം എന്നൊരു പ്രത്യേകകൂടി ഉണ്ടെങ്കിൽ അതെന്തായാലും ഒരു 3-സ്ഫിയറിന് തുല്യമാണ്. ടോപ്പോളജിയിൽ രണ്ടു ആകൃതികൾ തുല്യമാണ് എന്നതിന്റെ അർത്ഥം ഒരു ആകൃതിയെ മുറിയ്ക്കാതെ തന്നെ രൂപമാറ്റം വരുത്തി മറ്റേ ആകൃതി ആക്കി മാറ്റാം എന്നാണ്. ഉയർന്ന മാനങ്ങളിലുള്ള ഇടങ്ങളിൽ ഈ പ്രമേയം പണ്ടേ തെളിയിയ്ക്കപ്പെട്ടിട്ടുണ്ട്. ഏതാണ്ട് ഒരു ശതാബ്ദത്തോളം ഈ കൺജെക്ചർ തെളിയിയ്ക്കപ്പെടാതെ കിടന്നു. 2002-2003 വർഷങ്ങളിൽ ഗ്രിഗറി പെരിൽമാൻ എന്ന റഷ്യൻ ഗണിതശാസ്ത്രജ്ഞൻ ആർക്സിവ് വെബ്സൈറ്റിൽ ഇതിന്റ തെളിവ് ഉൾകൊള്ളുന്ന മൂന്ന് വ്യത്യസ്ത പ്രബന്ധങ്ങൾ പ്രസിദ്ധീകരിച്ചു. റിച്ചാർഡ്. എസ്. ഹാമിൽട്ടൺ തുടങ്ങി വെച്ച റിച്ചി ഫ്ലോ അടിസ്ഥാനമാക്കിയുള്ള തെളിവിനെ അടിസ്ഥാനമാക്കിയാണ് പെരിൽമാൻ തന്റെ തെളിവ് ഉണ്ടാക്കിയെടുത്തത്. അടിസ്ഥാന റിച്ചി ഫ്ലോ സങ്കേതത്തെ വ്യത്യാസപ്പെടുത്തി ഹാമിൽട്ടൺ തന്റെ ''സർജറി ഉൾക്കൊള്ളുന്ന റിച്ചി ഫ്ലോ'' എന്ന സങ്കേതം അവതരിപ്പിച്ചു. ഈ സങ്കേതത്തിൽ ഓരോ തവണയും ഒരു സിംഗുലാരിറ്റി കണ്ടെത്തുമ്പോൾ അതിനെ മുറിച്ചു മാറ്റുക എന്ന വിദ്യയാണ് അദ്ദേഹം പ്രയോഗിച്ചത്. എന്നാൽ മൂന്ന് മാനങ്ങളിൽ ഈ സങ്കേതം കോൺവെർജ് ചെയ്യും എന്ന് തെളിയിയ്ക്കാൻ അദ്ദേഹത്തിനായില്ല.[1] പേരെൽമാൻ ഈ ഭാഗമാണ് തെളിയിച്ചത്. പല ഗണിതശാസ്ത്രജ്ഞമാരും വെവ്വേറെയായി പെരെൽമാൻറെ തെളിവ് പരിശോധിച്ച് ശരിവെച്ചു. തെളിയിയ്ക്കപ്പെടുന്നതിന് മുൻപ് പോയിൻകാരെ കൺജെക്ചർ ടോപ്പോളജിയിലെ ഏറ്റവും പ്രധാനപ്പെട്ട സമസ്യകളിൽ ഒന്നായിരുന്നു. 2000-ത്തിൽ ഇത് സഹസ്രാബ്ദ പുരസ്കാര സമസ്യകളിൽ സ്ഥാനം പിടിച്ചു. ക്ലേ ഗണിതശാസ്ത്ര ഇൻസ്റ്റിറ്റ്യൂട്ട് ഇത് തെളിയിക്കുന്നവർക്ക് ഒരു ദശലക്ഷം അമേരിക്കൻ ഡോളർ സമ്മാനം പ്രഖ്യാപിച്ചിരുന്നു. 2006 ഓടെ വിശദമായ പരിശോധനകൾക്ക് ശേഷം ഗണിതശാസ്ത്രലോകം പെരെൽമാന്റെ തെളിവ് സ്വീകരിച്ചു. ഇതിനെത്തുടർന്ന് ഗണിതത്തിലെ പരമോന്നത ബഹുമതിയായ ഫീൽഡ്സ് മെഡൽ അദ്ദേഹത്തിന് നൽകാൻ തീരുമാനിച്ചെങ്കിലും[2] അദ്ദേഹം അത് നിരസിയ്ക്കുകയാണുണ്ടായത്. 2010 മാർച്ച് 18 ന് അദ്ദേഹത്തിന് സഹസ്രാബ്ദ പുരസ്കാര സമസ്യയുടെ പ്രതിഫലമായ ഒരു ദശലക്ഷം ഡോളർ നൽകാൻ ക്ലേ ഇൻസ്റ്റിറ്റ്യൂട്ട് തീരുമാനിച്ചു.[3] ജൂലൈ 1 നു അദ്ദേഹം അത് നിരസിച്ചു. റിച്ചാർഡ് ഹാമിൽട്ടൺ ഇതിനു വേണ്ടി ചെയ്ത സംഭാവനയെക്കാൾ കൂടുതലായി താനൊന്നും ചെയ്തിട്ടില്ല എന്നായിരുന്നു അദ്ദേഹം ഇതിനു കാരണമായി പറഞ്ഞത്.[4][5] 2018 വരെ സഹസ്രാബ്ദ പുരസ്കാര സമസ്യകളിലെ പോയിൻകാരെ കൺജെക്ചർ മാത്രമാണ് തെളിയിയ്ക്കപ്പെട്ടതായുള്ളത്. 2006 ഡിസംബർ 22 ന് സയൻസ് ജേർണൽ പെരെൽമാന്റെ തെളിവിനെ ''ബ്രേക്ക് ത്രൂ ഓഫ് ദി ഇയർ" എന്ന പദവി നൽകി ആദരിച്ചു. ഗണിതശാസ്ത്രവുമായി ബന്ധപ്പെട്ട ഒരു കണ്ടുപിടിത്തത്തിന് ഈ പദവി ലഭിച്ചത് ആദ്യമായാണ്.[6] അനൗപചാരിക വിവരണം[7]  ടോപ്പോളജിയിൽ രണ്ടു മാനങ്ങളുള്ള ഉപരിതലങ്ങളിൽ ഒരു ഗോളത്തിന്റെ (കൂടുതൽ കൃത്യമായി എഴുതിയാൽ 2-സ്ഫിയർ, ഒരു ഗോളത്തിന്റെ ഉപരിതലത്തിന് രണ്ടു മാനങ്ങൾ മാത്രമാണ് ഉള്ളത്, ഗോളം എന്നത് ത്രിമാന വസ്തു ആണെങ്കിലും അതിന്റെ ഉപരിതലം ദ്വിമാനമാണ്) ഉപരിതലം മാത്രമാണ് അടഞ്ഞതും (closed) എന്നാൽ ലഘുവായി സംബന്ധിതമായിട്ടുള്ളതും (simply connected). റ്റോപ്പോളോജിയിലെ ഗോളം എന്നത് ജ്യാമിതീയമായ ഗോളം തന്നെ ആകണമെന്നില്ല, മുറിയ്ക്കാതെ രൂപാന്തരം നടത്തി മാറ്റിയെടുക്കാവുന്ന ഏതൊരു ആകൃതിയും ഇതിൽ 'ഗോളം' ആണ്.[a] എന്നാൽ മൂന്നു മാനങ്ങളുള്ള ഉപരിതലങ്ങളിലും ഗോളം (3-സ്ഫിയർ, അഥവാ ഹൈപ്പർസ്ഫിയർ) തന്നെയാണോ ഈ പ്രത്യേകതകളുള്ള ഒരേ ഒരു പ്രതലം എന്നതാണ് പോയിൻകാരെ കൺജെക്ചർ.[b] നമ്മുടെ സാധാരണ ഗോളം പരിഗണിയ്ക്കുക (2-സ്ഫിയർ). ഇത്തരം ഒരു ഗോളത്തിനുമേൽ എങ്ങനെ കുരുക്കിട്ട് ആ കുരുക്ക് മുറുക്കാൻ ശ്രമിച്ചാലും അത് ഗോളത്തിനു പുറത്തുകൂടി ഊർന്ന് ഗോളവും കുരുക്കും വേർപെടും. അതായത് കുട്ടിക്കാലത്തെ കളികളിൽ നിന്നും ഒരു പന്തിന്റെ മുകളിലൂടെ ഒരു കുരുക്ക് ഇട്ട് ഊർന്നുപോകാതെ മുറുക്കാൻ സാധ്യമല്ല എന്ന കാര്യം വ്യക്തമാണല്ലോ. എന്നാൽ ഒരു ഉഴുന്നുവടയിൽ ഇങ്ങനെ ഊർന്നു പോകാതെ ഒരു കുരുക്കിടാൻ പറ്റും. ഉഴുന്നുവട രണ്ടായി മുറിച്ചാൽ മാത്രമേ ഈ കുരുക്ക് അഴിയ്ക്കാതെ പുറത്തെടുക്കാൻ കഴിയൂ. മുകളിലെ ചിത്രത്തിലെ ടോറസിൽ (ഉഴുന്നുവടയുടെ ആകൃതിയുടെ ഗണിതശാസ്ത്രനാമം) കൊടുത്തിരിയ്ക്കുന്ന രണ്ടു കുരുക്കുകളും ശ്രദ്ധിയ്ക്കുക. ഇവയെ വലിച്ചു ചുരുക്കി പുറത്തേയ്ക്ക് ഊർന്ന് എടുക്കാൻ പറ്റില്ല. പുറത്തെടുക്കണമെങ്കിൽ ഇവയെ മുറിച്ച് എടുക്കണം. കഴുത്തിൽ കുരുക്ക് ഇട്ടു നിറുത്തിയിരിക്കുന്ന ഒരു പശുവിനെ സങ്കൽപ്പിയ്ക്കുക. പശുവിന് ജ്യാമിതീയമായി ഗോളാകൃതി അല്ലെങ്കിലും ടോപ്പോളജി പ്രകാരം ഇത് ഗോളത്തിന് തുല്യമാണ്.[9] അതായത് പശുവിനെ രൂപാന്തരം നടത്തി ഒരു ഗോളമാക്കി മാറ്റാൻ സാധിയ്ക്കും. അതിനാൽ പശുവിന്റെ കുരുക്ക് ഊർന്ന് എടുക്കാൻ കഴിയാത്തതാണെന്ന് ഒറ്റനോട്ടത്തിൽ തോന്നുമെങ്കിലും പശുവിനെ മുറിയ്ക്കാതെ തന്നെ രൂപമാറ്റം നടത്തി കുരുക്ക് ഊർന്ന് എടുക്കാൻ സാധിയ്ക്കും. ഇതിനെ കുറച്ചുകൂടെ ശക്തമായ ഒരു പ്രസ്താവന ആക്കി ഇങ്ങനെ പറയാം. ത്രിമാന ഇടത്തിൽ ഇപ്രകാരം മുറിയ്ക്കാതെ തന്നെ കുരുക്കുകൾ മുറുക്കി ഊർന്ന് എടുക്കാവുന്ന എല്ലാ ദ്വിമാന പ്രതലങ്ങളും ഗോളങ്ങൾക്ക് തുല്യമാണ്. എന്നാൽ ചതുർമാന ഇടത്തിൽ ഇങ്ങനെ കുരുക്കുകൾ മുറിയ്ക്കാതെ ഊർന്ന് എടുക്കാവുന്ന എല്ലാ ത്രിമാന പ്രതലങ്ങളും 3-സ്ഫിയർ അഥവാ ഹൈപ്പർ സ്ഫിയറിനു തുല്യമാണോ? ഈ ചോദ്യമാണ് പോയിൻകാരെ കൺജെക്ചർ. ഗ്രിഗോറി പെരെൽമാൻ ഇതിന്റെ ഉത്തരം അതേ എന്നാണെന്ന് തെളിയിച്ചു. ഇതിനേക്കാൾ ഉയർന്ന മാനങ്ങളിലുള്ള ഉപരിതലങ്ങളുടെ കാര്യത്തിൽ ഈ ചോദ്യത്തിന്റെ ഉത്തരം 'അതെ' എന്നാണെന്ന് മുൻപേ തെളിയിച്ചിട്ടുണ്ട്.[10][11][12][13][14] കുറിപ്പുകൾ
അവലംബങ്ങൾ
കൂടുതൽ വായനയ്ക്ക്
പുറംകണ്ണികൾ
|
Portal di Ensiklopedia Dunia













