Ó©śÓ©¤Ó©ŠÓ©ģ 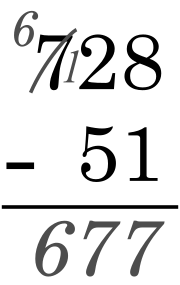 Ó©śÓ©¤Ó©ŠÓ©ģ Ó©ćÓ®▒Ó©Ģ Ó©ģÓ®░Ó©ĢÓ©ŚÓ©ŻÓ©┐Ó©żÓ©┐Ó©Ģ Ó©ĢÓ©┐Ó©░Ó©┐Ó©å Ó©╣Ó®ł Ó©£Ó©┐Ó©╣Ó®£Ó®Ć Ó©ĢÓ©┐Ó©ĖÓ®ć Ó©¢Ó©╝Ó©ŠÓ©Ė Ó©ĢÓ©┐Ó©ĖÓ©« Ó©”Ó®ć Ó©ĖÓ©«Ó®éÓ©╣ Ó©£Ó©ŠÓ©é Ó©ŁÓ®░Ó©ĪÓ©ŠÓ©░ Ó©ĄÓ©┐Ó®▒Ó©ÜÓ®ŗÓ©é Ó©ÜÓ®ĆÓ©£Ó©╝Ó©ŠÓ©é Ó©ĢÓ®▒Ó©óÓ©Ż Ó©©Ó®éÓ®░ Ó©”Ó©░Ó©ĖÓ©ŠÓ©ēÓ©éÓ©”Ó©Š Ó©╣Ó®łÓźż Ó©śÓ©¤Ó©ŠÓ©ģ Ó©”Ó®ć Ó©©Ó©żÓ®ĆÓ©£Ó®ć Ó©©Ó®éÓ®░ Ó©½Ó©╝Ó©░Ó©Ģ Ó©ĢÓ©┐Ó©╣Ó©Š Ó©£Ó©ŠÓ©éÓ©”Ó©Š Ó©╣Ó®łÓźż[1][2] Ó©śÓ©¤Ó©ŠÓ©ģ Ó©©Ó®éÓ®░ Ó©«Ó©ŠÓ©łÓ©©Ó©Ė Ó©”Ó®ć Ó©ÜÓ©┐Ó®░Ó©©Ó®ŹÓ©╣ (ŌłÆ) Ó©©Ó©ŠÓ©▓ Ó©”Ó©░Ó©ĖÓ©ŠÓ©ćÓ©å Ó©£Ó©ŠÓ©éÓ©”Ó©Š Ó©╣Ó®łÓźż Ó©ēÓ©”Ó©ŠÓ©╣Ó©░Ó©© Ó©▓Ó©ł, Ó©©Ó©ŠÓ©▓ Ó©”Ó©┐Ó®▒Ó©żÓ®Ć Ó©ŚÓ©ł Ó©żÓ©ĖÓ©ĄÓ®ĆÓ©░ Ó©ĄÓ©┐Ó®▒Ó©Ü 5 ŌłÆ 2 Ó©ĖÓ®ćÓ©¼ Ó©╣Ó©©, Ó©£Ó©┐Ó©ĖÓ©”Ó©Š Ó©«Ó©żÓ©▓Ó©¼ Ó©╣Ó®ł Ó©ĢÓ©┐ 5 Ó©ĄÓ©┐Ó®▒Ó©ÜÓ®ŗÓ©é 2 Ó©ĖÓ®ćÓ©¼ Ó©¼Ó©ŠÓ©╣Ó©░ Ó©ĢÓ®▒Ó©óÓ©Ż Ó©©Ó©ŠÓ©▓ Ó©¼Ó©ŠÓ©ĢÓ®Ć Ó©żÓ©┐Ó®░Ó©© Ó©ĖÓ®ćÓ©¼ Ó©¼Ó©ÜÓ©ŻÓ©ŚÓ®ćÓźż Ó©ćÓ©Ė Ó©ĢÓ©░Ó©ĢÓ®ć 5 Ó©ģÓ©żÓ®ć 2 Ó©”Ó©Š Ó©½Ó©╝Ó©░Ó©Ģ 3 Ó©╣Ó®ŗ Ó©£Ó©ŠÓ©éÓ©”Ó©Š Ó©╣Ó®ł; 5 ŌłÆ 2 = 3Óźż Ó©śÓ©¤Ó©ŠÓ©ģ Ó©╣Ó©«Ó®ćÓ©ĖÓ©╝Ó©Š Ó©ĄÓ®▒Ó©¢-Ó©ĄÓ®▒Ó©¢ Ó©żÓ©░Ó®ŹÓ©╣Ó©ŠÓ©é Ó©”Ó®ĆÓ©åÓ©é Ó©ÜÓ®ĆÓ©£Ó©╝Ó©ŠÓ©é Ó©ĄÓ©┐Ó®▒Ó©ÜÓ®ŗÓ©é Ó©¬Ó©”Ó©ŠÓ©░Ó©źÓ©Ģ Ó©ģÓ©żÓ®ć Ó©ŁÓ®īÓ©żÓ©┐Ó©Ģ Ó©ÜÓ®ĆÓ©£Ó©╝Ó©ŠÓ©é Ó©¼Ó©ŠÓ©╣Ó©░ Ó©ĢÓ®▒Ó©óÓ©Ż Ó©ģÓ©żÓ®ć Ó©śÓ®▒Ó©¤ Ó©ĢÓ©░Ó©© Ó©”Ó©Š Ó©ĖÓ®░Ó©ĢÓ®ćÓ©ż Ó©ĢÓ©░Ó©”Ó©Š Ó©╣Ó®ł Ó©ģÓ©żÓ®ć Ó©ćÓ©╣ Ó©░Ó©┐Ó©ŻÓ©ŠÓ©żÓ©«Ó©Ģ Ó©ģÓ®░Ó©ĢÓ©ŠÓ©é, Ó©ŁÓ©┐Ó®░Ó©© Ó©ģÓ®░Ó©ĢÓ©ŠÓ©é, Ó©ŚÓ®łÓ©░-Ó©¼Ó©¤Ó®ćÓ©©Ó®üÓ©«Ó©Š Ó©ĖÓ®░Ó©¢Ó©┐Ó©åÓ©ĄÓ©ŠÓ©é, Ó©ĄÓ®łÓ©ĢÓ©¤Ó©░Ó©ŠÓ©é, Ó©ĪÓ®łÓ©ĖÓ®ĆÓ©«Ó©▓Ó©ŠÓ©é, Ó©½Ó©╝Ó®░Ó©ĢÓ©ĖÓ©╝Ó©©Ó©ŠÓ©é Ó©ģÓ©żÓ®ć Ó©«Ó®łÓ©¤Ó©░Ó©┐Ó©ĢÓ©Ė Ó©▓Ó©ł Ó©ĄÓ©░Ó©żÓ©┐Ó©å Ó©£Ó©Š Ó©ĖÓ©ĢÓ©”Ó©Š Ó©╣Ó®łÓźż[1][2] Ó©śÓ©¤Ó©ŠÓ©ģ Ó©”Ó®ć Ó©ĢÓ®üÓ©Ø Ó©«Ó©╣Ó®▒Ó©żÓ©ĄÓ©¬Ó®éÓ©░Ó©© Ó©ŚÓ®üÓ©Ż Ó©╣Ó®üÓ®░Ó©”Ó®ć Ó©╣Ó©©Óźż Ó©ćÓ©╣ Ó©ÉÓ©éÓ©¤Ó®ĆÓ©ĢÓ®░Ó©«Ó®éÓ©¤Ó®ćÓ©¤Ó©┐Ó©Ą Ó©╣Ó®üÓ®░Ó©”Ó©Š Ó©╣Ó®ł, Ó©£Ó©┐Ó©ĖÓ©”Ó©Š Ó©«Ó©żÓ©▓Ó©¼ Ó©ćÓ©╣ Ó©╣Ó®ł Ó©ĢÓ©┐ Ó©£Ó®ćÓ©ĢÓ©░ Ó©ÜÓ®ĆÓ©£Ó©╝Ó©ŠÓ©é Ó©”Ó®ć Ó©ĢÓ®ŹÓ©░Ó©« Ó©¼Ó©”Ó©▓ Ó©”Ó©┐Ó®▒Ó©żÓ©Š Ó©£Ó©ŠÓ©ĄÓ®ć Ó©żÓ©ŠÓ©é Ó©åÓ©¢Ó©╝Ó©░Ó®Ć Ó©©Ó©żÓ®ĆÓ©£Ó®ć Ó©ēÓ®▒Ó©¬Ó©░ Ó©ćÓ©ĖÓ©”Ó©Š Ó©ĖÓ©┐Ó®▒Ó©¦Ó©Š Ó©¬Ó®ŹÓ©░Ó©ŁÓ©ŠÓ©Ą Ó©╣Ó®üÓ®░Ó©”Ó©Š Ó©╣Ó®ł, Ó©ÜÓ©ŠÓ©╣Ó®ć Ó©ćÓ©╣ Ó©żÓ©¼Ó©”Ó®ĆÓ©▓Ó®Ć Ó©ĢÓ©┐Ó®░Ó©©Ó®Ć Ó©ĄÓ®Ć Ó©øÓ®ŗÓ©¤Ó®Ć Ó©ĢÓ©┐Ó©ēÓ©é Ó©©Ó©Š Ó©╣Ó®ŗÓ©ĄÓ®ćÓźż Ó©ćÓ©╣ Ó©ĖÓ©╣Ó©┐Ó©»Ó®ŗÓ©ŚÓ®Ć Ó©ĄÓ®Ć Ó©©Ó©╣Ó®ĆÓ©é Ó©╣Ó®ł, Ó©£Ó©┐Ó©ĖÓ©”Ó©Š Ó©«Ó©żÓ©▓Ó©¼ Ó©ćÓ©╣ Ó©╣Ó®ł Ó©ĢÓ©┐ Ó©£Ó®ćÓ©ĢÓ©░ Ó©ĢÓ®ŗÓ©ł Ó©”Ó®ŗ Ó©żÓ®ŗÓ©é Ó©ĄÓ©¦Ó®ćÓ©░Ó®ć Ó©ģÓ®░Ó©ĢÓ©ŠÓ©é Ó©ĄÓ©┐Ó®▒Ó©Ü Ó©śÓ©¤Ó©ŠÓ©ģ Ó©ĢÓ©░Ó©”Ó©Š Ó©╣Ó®ł Ó©żÓ©ŠÓ©é, Ó©£Ó©┐Ó©╣Ó®£Ó®ć Ó©ĢÓ®ŹÓ©░Ó©« Ó©ĄÓ©┐Ó®▒Ó©Ü Ó©śÓ©¤Ó©ŠÓ©ģ Ó©ĢÓ®ĆÓ©żÓ©Š Ó©ŚÓ©┐Ó©å Ó©╣Ó®ł, Ó©ēÓ©╣ Ó©¼Ó©╣Ó®üÓ©ż Ó©«Ó©╣Ó®▒Ó©żÓ©ĄÓ©¬Ó®éÓ©░Ó©© Ó©╣Ó®üÓ®░Ó©”Ó©Š Ó©╣Ó®ł Ó©ģÓ©żÓ®ć Ó©ģÓ©ŚÓ©▓Ó®Ć Ó©ĄÓ©ŠÓ©░ Ó©ēÓ©╣Ó®Ć Ó©ĖÓ©┐Ó®▒Ó©¤Ó©Š Ó©╣Ó©ŠÓ©ĖÓ©┐Ó©▓ Ó©ĢÓ©░Ó©© Ó©▓Ó©ł Ó©ĖÓ©ŠÓ©©Ó®éÓ®░ Ó©ēÓ©╣Ó®Ć Ó©ćÓ®▒Ó©Ģ Ó©ĢÓ®ŹÓ©░Ó©« Ó©ĄÓ©┐Ó®▒Ó©Ü Ó©śÓ©¤Ó©ŠÓ©ģ Ó©ĢÓ©░Ó©©Ó©Š Ó©¬Ó©ĄÓ®ćÓ©ŚÓ©ŠÓźż 0 Ó©©Ó®éÓ®░ Ó©ĢÓ©┐Ó©ĖÓ®ć Ó©ĄÓ®Ć Ó©ģÓ®░Ó©Ģ Ó©£Ó©ŠÓ©é Ó©ĖÓ®░Ó©¢Ó©┐Ó©å Ó©ĄÓ©┐Ó®▒Ó©ÜÓ®ŗÓ©é Ó©śÓ©¤Ó©ŠÓ©ēÓ©Ż Ó©©Ó©ŠÓ©▓ Ó©ĢÓ®ŗÓ©ł Ó©½Ó©╝Ó©░Ó©Ģ Ó©©Ó©╣Ó®ĆÓ©é Ó©¬Ó®łÓ©éÓ©”Ó©ŠÓźż Ó©śÓ©¤Ó©ŠÓ©ģ, Ó©£Ó®ŗÓ®£ Ó©ģÓ©żÓ®ć Ó©ŚÓ®üÓ©ŻÓ©Š Ó©”Ó®ĆÓ©åÓ©é Ó©ĢÓ©┐Ó©░Ó©┐Ó©åÓ©ĄÓ©ŠÓ©é Ó©ĄÓ©┐Ó®▒Ó©Ü Ó©ŁÓ©ĄÓ©┐Ó®▒Ó©¢Ó©ż Ó©©Ó©┐Ó©»Ó©« Ó©«Ó®░Ó©©Ó©”Ó©Š Ó©╣Ó®łÓźż Ó©ćÓ©╣ Ó©ĖÓ©ŠÓ©░Ó®ć Ó©©Ó©┐Ó©»Ó©« Ó©ĖÓ©ŠÓ©¼Ó©┐Ó©ż Ó©ĢÓ®ĆÓ©żÓ®ć Ó©£Ó©Š Ó©ÜÓ®üÓ®▒Ó©ĢÓ®ć Ó©╣Ó©©Óźż Ó©śÓ©¤Ó©ŠÓ©ģ Ó©ĢÓ©░Ó©©Ó©Š Ó©╣Ó©┐Ó©ĖÓ©ŠÓ©¼ Ó©”Ó®ĆÓ©åÓ©é Ó©ĢÓ©┐Ó©░Ó©┐Ó©åÓ©ĄÓ©ŠÓ©é Ó©ĄÓ©┐Ó®▒Ó©ÜÓ®ŗÓ©é Ó©£Ó®ŗÓ®£ Ó©żÓ®ŗÓ©é Ó©¬Ó©┐Ó®▒Ó©øÓ®ŗÓ©é Ó©ĖÓ©Ł Ó©żÓ®ŗÓ©é Ó©åÓ©ĖÓ©ŠÓ©© Ó©ĢÓ®░Ó©« Ó©╣Ó®łÓźż Ó©øÓ®ŗÓ©¤Ó®ć Ó©ģÓ®░Ó©ĢÓ©ŠÓ©é Ó©”Ó©Š Ó©śÓ©¤Ó©ŠÓ©ģ Ó©¼Ó©╣Ó®üÓ©ż Ó©øÓ®ŗÓ©¤Ó®Ć Ó©ēÓ©«Ó©░ Ó©”Ó®ć Ó©¼Ó®▒Ó©ÜÓ®ć Ó©ĄÓ®Ć Ó©ĢÓ©░ Ó©▓Ó®łÓ©éÓ©”Ó®ć Ó©╣Ó©©Óźż Ó©«Ó®üÓ®▒Ó©óÓ©▓Ó®Ć Ó©ĖÓ©┐Ó®▒Ó©¢Ó©┐Ó©å Ó©ĄÓ©┐Ó®▒Ó©Ü Ó©¼Ó®▒Ó©ÜÓ©┐Ó©åÓ©é Ó©©Ó®éÓ®░ Ó©ĪÓ®łÓ©ĖÓ®ĆÓ©«Ó©▓ Ó©ĖÓ©┐Ó©ĖÓ©¤Ó©« Ó©ĄÓ©┐Ó®▒Ó©Ü Ó©śÓ©¤Ó©ŠÓ©ģ Ó©ĢÓ©░Ó©©Ó©Š Ó©ĖÓ©┐Ó©¢Ó©ŠÓ©ćÓ©å Ó©£Ó©ŠÓ©éÓ©”Ó©Š Ó©╣Ó®ł Ó©£Ó©┐Ó©Ė Ó©ĄÓ©┐Ó®▒Ó©Ü Ó©ćÓ®▒Ó©Ģ Ó©ģÓ®░Ó©Ģ Ó©╣Ó®Ć Ó©╣Ó®üÓ®░Ó©”Ó®ć Ó©╣Ó©© Ó©ģÓ©żÓ®ć Ó©«Ó©ŚÓ©░Ó®ŗÓ©é Ó©ćÓ©©Ó®ŹÓ©╣Ó©ŠÓ©é Ó©©Ó®éÓ®░ Ó©ĖÓ©┐Ó®▒Ó©¢ Ó©ĢÓ®ć Ó©¼Ó®▒Ó©ÜÓ®ć Ó©ĄÓ©¦Ó®ćÓ©░Ó®ć Ó©«Ó®üÓ©ĖÓ©╝Ó©ĢÓ©▓ Ó©ĖÓ©ĄÓ©ŠÓ©▓Ó©ŠÓ©é Ó©©Ó®éÓ®░ Ó©╣Ó®▒Ó©▓ Ó©ĢÓ©░Ó©©Ó©Š Ó©ĖÓ©┐Ó®▒Ó©¢Ó©”Ó®ć Ó©╣Ó©©Óźż Ó©ĖÓ®░Ó©ĢÓ®ćÓ©ż Ó©ģÓ©żÓ®ć Ó©¬Ó©░Ó©┐Ó©ŁÓ©ŠÓ©ĖÓ©╝Ó©┐Ó©Ģ Ó©ĖÓ©╝Ó©¼Ó©”Ó©ŠÓ©ĄÓ©▓Ó®ĆÓ©śÓ©¤Ó©ŠÓ©ģ Ó©©Ó®éÓ®░ Ó©åÓ©« Ó©żÓ®īÓ©░ 'Ó©żÓ®ć Ó©ĖÓ®░Ó©¢Ó©┐Ó©åÓ©ĄÓ©ŠÓ©é Ó©”Ó®ć Ó©ĄÓ©┐Ó©ÜÓ©ĢÓ©ŠÓ©░ Ó©«Ó©ŠÓ©łÓ©©Ó©Ė Ó©ÜÓ©┐Ó®░Ó©©Ó®ŹÓ©╣ "ŌłÆ" Ó©©Ó©ŠÓ©▓ Ó©”Ó©░Ó©ĖÓ©ŠÓ©ćÓ©å Ó©£Ó©ŠÓ©éÓ©”Ó©Š Ó©╣Ó®łÓźż Ó©ģÓ©¤Ó©ŠÓ©ģ Ó©”Ó®ć Ó©©Ó©żÓ®ĆÓ©£Ó®ć Ó©©Ó®éÓ®░ Ó©¼Ó©░Ó©ŠÓ©¼Ó©░ Ó©”Ó®ć Ó©ÜÓ©┐Ó®░Ó©©Ó®ŹÓ©╣ Ó©«Ó©ŚÓ©░Ó®ŗÓ©é Ó©▓Ó©┐Ó©¢Ó©┐Ó©å Ó©£Ó©ŠÓ©éÓ©”Ó©Š Ó©╣Ó®łÓźż Ó©ēÓ©”Ó©ŠÓ©╣Ó©░Ó©© Ó©”Ó®ć Ó©▓Ó©ł,
Ó©╣Ó©ĄÓ©ŠÓ©▓Ó®ć
|
Portal di Ensiklopedia Dunia





















