Копроизведение

Копроизведение (категорная сумма) семейства объектов — обобщение в теории категорий понятий дизъюнктного объединения множеств и топологических пространств и прямой суммы модулей или векторных пространств. Копроизведение семейства объектов — это «наиболее общий» объект, в который существует морфизм из каждого объекта семейства. Копроизведение объектов двойственно их произведению, то есть определение копроизведения можно получить из определения произведения обращением всех стрелок. Тем не менее, во многих категориях произведение и копроизведение объектов разительно отличаются.

Определение

Пусть ${\mathcal {C}}$ — категория, $\{X_{j}|j\in J\}$ — индексированное семейство её объектов. Копроизведение этого семейства — это объект $X$ , вместе с морфизмами $i_{j}\colon \,X_{j}\to X$ , называемыми каноническими вложениями, такой что для любого объекта $Y$ категории ${\mathcal {C}}$ и семейства морфизмов $f_{j}\colon \,X_{j}\to Y$ существует единственный морфизм $f\colon \,X\to Y$ , такой что $f_{j}=f\circ i_{j}$ , то есть следующая диаграмма коммутативна для каждого $j$ :

Копроизведение семейства $\{X_{j}\}$ обычно обозначают

X=\coprod _{j\in J}X_{j}

или

X=\bigoplus _{j\in J}X_{j}.

Иногда морфизм $f$ обозначают

f=\coprod _{j\in J}f_{j}:\coprod _{j\in J}X_{j}\to Y

чтобы подчеркнуть его зависимость от $f_{j}$ .

Копроизведение двух объектов обычно обозначают $X_{1}\coprod X_{2}$ или $X_{1}\oplus X_{2}$ , тогда диаграмма принимает вид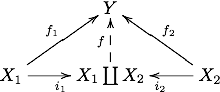

Соответственно, $f$ обозначают при этом $f_{1}\coprod f_{2}$ , $f_{1}\oplus f_{2}$ или $[f_{1},f_{2}]$ .

Единственность результата операции $[-,-]$ можно альтернативно выразить как равенство $[h\circ i_{1},h\circ i_{2}]=h$ , верное для любых $h$ .^[1]

Существует эквивалентное определение копроизведения. Копроизведение семейства $\{X_{j}|j\in J\}$ — это такой объект $X$ , что для любого объекта $Y\in C$ функция ${\text{Hom}}(X,Y)\rightarrow \prod _{j\in J}{\text{Hom}}(X_{j},Y)$ , заданная как $u\mapsto \{u\circ i_{j}\}$ , биективна.^[2]

Примеры

В категории множеств копроизведение семейства множеств — это их дизъюнктное объединение, канонические отображения $i_{j}$ — это очевидные вложения. Универсальное свойство в данном случае можно переговорить таким образом: для того, чтобы задать функцию на дизъюнктном объединении, достаточно (и необходимо) задать функцию на каждой из его компонент.
В категориях векторных пространств, модулей и абелевых групп копроизведение называется прямой суммой.
В категории всех групп копроизведение — это свободное произведение.
В категории топологических пространств копроизведение — это дизъюнктное объединение множеств-носителей исходных пространств, а база топологии получается объединением (точнее, образами при канонических вложениях) исходных баз.

Свойства

Если сумма объектов существует, то она единственна с точностью до изоморфизма.
Коммутативность: $a+b\simeq b+a.$
Ассоциативность: $(a+b)+c\simeq a+(b+c)$
Если в категории существует начальный объект $\ 0$ , то $a+0\simeq 0+a\simeq a.$
Категория, в которой существуют копроизведения любого множества объектов — пример симметричной моноидальной категории.

Дистрибутивность

В общем случае существует канонический морфизм $X\times Y+X\times Z\to X\times (Y+Z)$ , где плюс обозначает копроизведение объектов. Это следует из существования канонических проекций и вложений и из коммутативности следующей диаграммы:

Универсальное свойство $X\times (Y+Z)$ гарантирует при этом существование искомого морфизма. Категория называется дистрибутивной, если в ней этот морфизм является изоморфизмом.

См. также

Матрица преобразований — категорный аналог матрицы линейного преобразования.
Пределы и копределы

Примечания

↑ Lambek J., Scott P. J. Introduction to Higher-Order Categorical Logic. — Cambridge University Press, 1988. — С. 304.
↑ Букур И., Деляну А. Введение в теорию категорий и функторов. — М.: «Мир», 1972.