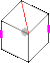
Кубик «Вертолёт»

Кубик «Вертолёт» — шарнирная головоломка, придуманная Адамом Г. Кованом в 2005 году и воплощённая в 2006^{[1][2][3][4][5][6][7]}.

Кубик «вертолёт» сделан в форме куба и разрезан на 8 угловых кусков и 24 кусков граней. Каждая угловая часть имеет 3 цвета, а каждая часть грани имеет единственный цвет. В отличие от кубика Рубика, грани вертолёта не вращаются, вращаются его рёбра.

Поворот ребра на 180° переставляет угловые части и переставляет две пары центральных кусков, но форма кубика сохраняется. Вся головоломка может быть перемешана таким образом.

Однако есть возможность повернуть ребро на угол примерно ~71°, из-за чего базовые плоскости двух групп угловых частей и центральных частей располагаются на плоскости вращения другого ребра. Тогда второе ребро может быть повёрнуто, смешивая угловые части и центральные части, нарушая кубическую форму головоломки. Этот вид перемешивания известен как смешанный поворот. Вследствие разного вида перемешанных частей некоторые повороты становятся невозможными в смешанной форме. Используя комбинацию таких «смешанных» вращений, можно вернуться к форме куба, но некоторые центральные части окажутся с неверной ориентацией, выступая в виде шипов, и не будут лежать плоско на грани куба. Могут случаться и более тонкие изменения, которые описаны ниже.

• 
  Перемешанный вертолёт
• 
  Поворот на ~71° при подготовке к смешанному вращению
• 
  Начало смешанного вращения
• 
  Полностью перемешанный вертолёт с помощью смешанных поворотов

Если головоломка перемешана только с помощью поворотов рёбер на 180°, то очевидно, что её можно решить с помощью таких же поворотов на 180°. Однако, если были сделаны некоторые смешанные вращения, даже если форма кубика опять стала кубической, может оказаться невозможным собрать кубик, используя только повороты на 180°. Причина в том, что при поворотах на 180° каждая центральная часть грани может поменять место в цикле, вовлекающем 6 частей, что называют орбитой части^[6]. Центральные части граней на различных орбитах не могут быть обменены при использовании поворотов на 180°. Однако смешанные вращения способны перевести центральные части грани на другие орбиты, что приводит головоломку в состояние, которое нельзя решить поворотами на 180° рёбер.

Предположим, что вертолёт перемешан без использования смешанных ходов (то есть только поворотами на 180 градусов). Возможны любые перестановки углов, включая нечётные. Семь углов могут вращаться независимо, а ориентация восьмого зависит от остальных семи, что даёт 8!×3⁷ комбинаций.

Имеется 24 центральных частей граней, которые могут быть переставлены 24! различными способами. Но центральные части фактически оказываются на 4 различных орбитах, каждая из которых содержит все цвета. Таким образом, число перестановок сокращается до 6!^4[8]. Перестановки центральных частей чётны, так что число перестановок делится на 2.

Если рассматривать куб не фиксированным в пространстве, а положения, которые получаются вращениями куба без смешивания, считаются идентичными, число перестановок уменьшается в 24 раза. Это потому, что все 24 положения и ориентации первого угла эквивалентны ввиду отсутствия фиксирования центров. Этот множитель не возникает, когда вычисляются перестановки N×N×N куба при нечётном N, поскольку эти головоломки имеют фиксированные центры, которые определяют пространственную ориентацию куба.

Это даёт полное число перестановок:

${\displaystyle {\frac {7!\cdot 3^{6}\cdot 6!^{4}}{2}}\approx 4.94\times 10^{17}.}$

В десятичной форме это равно 493.694.233.804.800.000 (примерно 494 квадриллиона по длинной шкале)^[6].

Когда вертолёт перемешан со смешанными вращениями, но форма осталась кубической, то центральные части не оказываются на 4 различных орбитах. Предположим, что четыре центральных части каждого цвета неразличимы, число перестановок равно 24!/(4!⁶). Число получается из того, что имеется 24 (4!) способов расставить четыре куска данного цвета. Степень возникает из наличия шести цветов.

Это даёт полное число перестановок:

${\displaystyle {\frac {7!\cdot 3^{6}\cdot 24!}{4!^{6}}}.}$

В десятичной форме это равно 11.928.787.020.628.077.600.000 (примерно 12 секстиллионов по длинной шкале)^[8].

Чтобы посчитать число позиций, когда теряется форма куба, нам нужно посчитать все возможные формы (игнорируя цвета). Подсчитать эти формы затруднительно, поскольку иногда ходы блокируются формой кусков, а не механизмом головоломки. Матт Галла сделал полный анализ и выложил свои результаты здесь на форуме TwistyPuzzles. Он обнаружил 14.098 форм, или 28.055, если зеркальные формы считаются различающимися. Некоторые из этих форм имеют, однако, симметрию, и дают менее 24 (или 48) возможных ориентаций. Ниже перечислены эти симметрии^[8]:

Симметрия		mr4r3r2	mr3r2	r3r2	mfr2e	mer2e	r2er2e	m4	me	r2e	r2f	mc	i	Всего
	Междун.	Oh	D3d	D3	C2v	C2h	D2	S4	Cs	C2	C2	S2	C1
	Шёнфлис	m3m	3m	322	mm2	2/m	222	4	m	2	2	1	1
Порядок		48	12	6	4	4	4	4	2	2	2	2	1
Индекс		1	4	8	12	12	12	12	24	24	24	24	48
Формы зеркало		1	1	8	1	18	4	1	82	764	5	37	13.176	14.098
		1	1	16	1	18	8	1	82	1.528	10	37	26.352	28.055
Всего		1	4	128	12	216	96	12	1.968	36.672	240	888	1.264.896	1.305.133

Строка «Порядок» показывает размер групп симметрии. Строка «Индекс» отражает индекс группы симметрии как подгруппы полной группы симметрии куба, то есть 48, делённое на порядок. Индекс является также числом способов ориентации конкретной формы в пространстве (включая отражения). Первая строка «Формы» даёт число форм, которые Матт нашёл для каждой группы симметрии, но без учёта зеркальных отражений, вторая строка включает зеркальные отражения. Строка «Всего» равна произведению индекса и числа форм ^[8].

Умножая это на предыдущий результат, получим 15.568.653.590.593.384.802.320.800.000 (примерно 15 квадриллиардов по длинной шкале) смешанных позиций^[8].

Имеется восемь вариантов вертолёта:

• оригинальный вертолёт, изготовленный компанией «The Twisty Store» (продавал также Уве Мефферт^[англ.]), состоял только из 8 угловых частей и 24 центральных частей граней;
• «Криволинейный вертолёт» Тома ван дер Зандена^[4] имеет 12 рёберных частей с 2 цветами. Это потребует от собирающего кубик выстроить рёберные части, в то время как у вертолёта эти части скрыты и не имеет значения, где они окажутся.
• «Криволинейный вертолёт плюс», также созданный Томом ван дер Занденом, имеет дополнительные рассечения центральных частей граней, что позволяет смешивать части даже больше;
• «Скьюб-вертолёт», опять же Тома ван дер Зандена, который выглядит в точности как оригинальный вертолёт, но может вращаться и как скьюб.
• «Криволинейный вертолёт 3», разрезы проходят через друг друга, эти пересечения образуют центры и 4 лепестка вокруг них. Также является гексаэдрическим аналогом мастер пираморфикса.
• «Цветочный/цветковый вертолёт». Это гибрид криволинейного дино куба и криволинейного вертолёта.
• Мастер маленькая отбивнушка — разрез ещё глубже, чем на 3 бабочке.
• Маленькая отбивнушка (Хром) — самый глубокий разрез из возможных. Пополам, посередине.

Также существует двойственная вертолёту головоломка Самоцвет 1, усложнённая его версия Самоцвет 7, у которого искажённые несимметричные шестиугольники, и октаэдр с более глубокими разрезами edge turning октаэдр Эйтана, являющийся двойственной головоломкой к криволинейному вертолёту 3. Так как тетраэдр двойственен сам себе, edge turning октаэдр Эйтана — это октаэдрический аналог мастер пираморфикса.

Гибрид криволинейного кубика Рубика 3х3х3 и бабочки. У неё есть двойственная головоломка — Самоцвет 10. На вид идентичен Самоцвету 1, но, помимо рёберных вращений, повороты квадратных сторон также доступны.

Если превратить криволинейный вертолёт плюс в ромбододекаэдр, то получится головоломка Crazy Comet. Из последней головоломки сделали версию под названием Глаза Небес (англ. Heaven’s eyes), в которой грани можно повернуть на половину поворота, однако, это возможно только благодаря маленькому слабозаметому довороту деталей после каждого движения.

Если у криволинейного вертолёта 3 спрятать 6 центров и 24 ребра и превратить получившееся в ромбододекаэдр, то получится 2х2х2 face turning ромбододекаэдр (Rua).

Самоцвет 9 — мастер маленькая отбившунка, урезанная до усечённого октаэдра. Эта головоломка есть также в форме идеального шара с различным расположением цветов и сторон и полостью в каждой детали.

Цилиндрический хромовый куб 24 — модификация маленькой отбивнушки (Хрома) в форму цилиндра.

У этой статьи есть несколько проблем, помогите их исправить: Необходимо проверить качество перевода c неуказанного языка, исправить содержательные и стилистические ошибки. Вы можете помочь улучшить эту статью (см. также рекомендации по переводу). Оригинал не указан. Пожалуйста, укажите его. (11 апреля 2020) Стиль этой статьи неэнциклопедичен или нарушает нормы литературного русского языка. Статью следует исправить согласно стилистическим правилам Википедии. (11 апреля 2020) Пожалуйста, после исправления проблемы исключите её из списка параметров. После устранения всех недостатков этот шаблон может быть удалён любым участником.