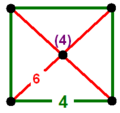
–ě–ļ—ā–į—ć–ī—Ä–į–Ľ—Ć–Ĺ—č–Ķ —Ā–ĺ—ā—č –Ņ–ĺ—Ä—Ź–ī–ļ–į 4
| –ě–ļ—ā–į—ć–ī—Ä–į–Ľ—Ć–Ĺ—č–Ķ —Ā–ĺ—ā—č –Ņ–ĺ—Ä—Ź–ī–ļ–į 4
|

–ü–Ķ—Ä—Ā–Ņ–Ķ–ļ—ā–ł–≤–Ĺ–į—Ź –Ņ—Ä–ĺ–Ķ–ļ—Ü–ł—Ź
–≤ –ľ–ĺ–ī–Ķ–Ľ–ł –ü—É–į–Ĺ–ļ–į—Ä–Ķ
|
| –Ę–ł–Ņ |
–ď–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–ł—á–Ķ—Ā–ļ–ł–Ķ –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ—č–Ķ —Ā–ĺ—ā—č
–ü–į—Ä–į–ļ–ĺ–ľ–Ņ–į–ļ—ā–Ĺ—č–Ķ –ĺ–ī–Ĺ–ĺ—Ä–ĺ–ī–Ĺ—č–Ķ —Ā–ĺ—ā—č[–į–Ĺ–≥–Ľ.]
|
–°–ł–ľ–≤–ĺ–Ľ—č –®–Ľ–Ķ—Ą–Ľ–ł|{3,4,4}
{3,41,1}
|
–Ē–ł–į–≥—Ä–į–ľ–ľ—č
–ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į ‚ÄĒ –Ē—č–Ĺ–ļ–ł–Ĺ–į |
      
     ‚ÜĒ ‚ÜĒ       
     ‚ÜĒ ‚ÜĒ       
     ‚ÜĒ ‚ÜĒ       
|
| –Į—á–Ķ–Ļ–ļ–ł |
–ĺ–ļ—ā–į—ć–ī—Ä {3,4}
|
| –ď—Ä–į–Ĺ–ł |
—ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ {3}
|
| –ö—Ä–į–Ķ–≤–į—Ź —Ą–ł–≥—É—Ä–į |
–ļ–≤–į–ī—Ä–į—ā {4}
|
| –í–Ķ—Ä—ą–ł–Ĺ–Ĺ–į—Ź —Ą–ł–≥—É—Ä–į |
–ö–≤–į–ī—Ä–į—ā–Ĺ—č–Ļ –Ņ–į—Ä–ļ–Ķ—ā, {4,4}
   
|
| –Ē–≤–ĺ–Ļ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ —Ā–ĺ—ā—č |
–ö–≤–į–ī—Ä–į—ā–Ĺ—č–Ķ –ľ–ĺ–∑–į–ł—á–Ĺ—č–Ķ —Ā–ĺ—ā—č[–į–Ĺ–≥–Ľ.], {4,4,3}
|
| –ď—Ä—É–Ņ–Ņ—č –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į |
[4,4,3]
[3,41,1]
|
| –°–≤–ĺ–Ļ—Ā—ā–≤–į |
–ü—Ä–į–≤–ł–Ľ—Ć–Ĺ—č–Ķ
|
–í –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–ł—á–Ķ—Ā–ļ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł 3 –≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ —Ā–ĺ—ā—č –Ņ–ĺ—Ä—Ź–ī–ļ–į 4 ‚ÄĒ –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ—č–Ķ –Ņ–į—Ä–į–ļ–ĺ–ľ–Ņ–į–ļ—ā–Ĺ—č–Ķ —Ā–ĺ—ā—č. –ě–Ĺ–ł –Ĺ–į–∑—č–≤–į—é—ā—Ā—Ź –Ņ–į—Ä–į–ļ–ĺ–ľ–Ņ–į–ļ—ā–Ĺ—č–ľ–ł, –Ņ–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É –ł–ľ–Ķ—é—ā –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ—č–Ķ –≤–Ķ—Ä—ą–ł–Ĺ–Ĺ—č–Ķ —Ą–ł–≥—É—Ä—č —Ā–ĺ –≤—Ā–Ķ–ľ–ł –≤–Ķ—Ä—ą–ł–Ĺ–į–ľ–ł –ļ–į–ļ –ł–ī–Ķ–į–Ľ—Ć–Ĺ—č–Ķ —ā–ĺ—á–ļ–ł –Ĺ–į –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ—Ā—ā–ł. –ē—Ā–Ľ–ł –ľ–Ĺ–ĺ–≥–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ –∑–į–ī–į–Ĺ —Ā–ł–ľ–≤–ĺ–Ľ–ĺ–ľ –®–Ľ–Ķ—Ą–Ľ–ł {3,4,4}, –ĺ–Ĺ –ł–ľ–Ķ–Ķ—ā —á–Ķ—ā—č—Ä–Ķ –ĺ–ļ—ā–į—ć–ī—Ä–į {3,4} –≤–ĺ–ļ—Ä—É–≥ –ļ–į–∂–ī–ĺ–≥–ĺ —Ä–Ķ–Ī—Ä–į –ł –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–Ķ —á–ł—Ā–Ľ–ĺ –ĺ–ļ—ā–į—ć–ī—Ä–ĺ–≤ –≤–ĺ–ļ—Ä—É–≥ –ļ–į–∂–ī–ĺ–Ļ –≤–Ķ—Ä—ą–ł–Ĺ—č –≤ –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ–ľ –Ņ–į—Ä–ļ–Ķ—ā–Ķ {4,4}, –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –≤–Ķ—Ä—ą–ł–Ĺ[–į–Ĺ–≥–Ľ.][1].
–ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ā–ĺ—ā—č ‚ÄĒ —ć—ā–ĺ –∑–į–Ņ–ĺ–Ľ–Ĺ—Ź—é—Č–ł–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –ľ–Ĺ–ĺ–≥–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–ł –ł–Ľ–ł —Ź—á–Ķ–Ļ–ļ–ł –Ī–ĺ–Ľ—Ć—ą–Ķ–Ļ —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł. –ó–į–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ—Ä–ĺ–ł—Ā—Ö–ĺ–ī–ł—ā —ā–į–ļ, —á—ā–ĺ –ľ–Ķ–∂–ī—É –Ĺ–ł–ľ–ł –Ĺ–Ķ –ĺ—Ā—ā–į—Ď—ā—Ā—Ź –∑–į–∑–ĺ—Ä–ĺ–≤. –≠—ā–ĺ –Ņ—Ä–ł–ľ–Ķ—Ä –Ī–ĺ–Ľ–Ķ–Ķ –ĺ–Ī—Č–Ķ–≥–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź –ľ–ĺ–∑–į–ł–ļ–ł –ł–Ľ–ł –∑–į–ľ–ĺ—Č–Ķ–Ĺ–ł—Ź –≤ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ –Ľ—é–Ī–ĺ–Ļ —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł.
–°–ĺ—ā—č –ĺ–Ī—č—á–Ĺ–ĺ —Ā—ā—Ä–ĺ—Ź—ā—Ā—Ź –≤ –ĺ–Ī—č—á–Ĺ–ĺ–ľ –Ķ–≤–ļ–Ľ–ł–ī–ĺ–≤–ĺ–ľ (¬ę–Ņ–Ľ–ĺ—Ā–ļ–ĺ–ľ¬Ľ) –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ĺ –≤—č–Ņ—É–ļ–Ľ—č–ľ –ĺ–ī–Ĺ–ĺ—Ä–ĺ–ī–Ĺ—č–ľ —Ā–ĺ—ā–į–ľ[–į–Ĺ–≥–Ľ.]. –ė—Ö –ľ–ĺ–∂–Ĺ–ĺ –Ņ–ĺ—Ā—ā—Ä–ĺ–ł—ā—Ć —ā–į–ļ–∂–Ķ –≤ –Ĺ–Ķ–Ķ–≤–ļ–Ľ–ł–ī–ĺ–≤—č—Ö –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į—Ö, —ā–į–ļ–ł–Ķ –ļ–į–ļ –ĺ–ī–Ĺ–ĺ—Ä–ĺ–ī–Ĺ—č–Ķ –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–ł—á–Ķ—Ā–ļ–ł–Ķ —Ā–ĺ—ā—č[–į–Ĺ–≥–Ľ.]. –õ—é–Ī–ĺ–Ļ –ļ–ĺ–Ĺ–Ķ—á–Ĺ—č–Ļ –ĺ–ī–Ĺ–ĺ—Ä–ĺ–ī–Ĺ—č–Ļ –ľ–Ĺ–ĺ–≥–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć —Ā–Ņ—Ä–ĺ–Ķ—Ü–ł—Ä–ĺ–≤–į–Ĺ –Ĺ–į –Ķ–≥–ĺ –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ—É—é —Ā—Ą–Ķ—Ä—É –ī–Ľ—Ź –ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł—Ź –ĺ–ī–Ĺ–ĺ—Ä–ĺ–ī–Ĺ—č—Ö —Ā–ĺ—ā –≤ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ.
–°–ł–ľ–ľ–Ķ—ā—Ä–ł—Ź
–ü–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ —Ā –Ņ–ĺ–Ľ–ĺ–≤–ł–Ĺ–Ĺ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ķ–Ļ, [3,4,4,1+], —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –ļ–į–ļ {3,41,1}, —Ā —á–Ķ—Ä–Ķ–ī–ĺ–≤–į–Ĺ–ł–Ķ–ľ –ī–≤—É—Ö –≤–ł–ī–ĺ–≤ (—Ü–≤–Ķ—ā–ĺ–≤) –ĺ–ļ—ā–į—ć–ī—Ä–į–Ľ—Ć–Ĺ—č—Ö —Ź—á–Ķ–Ķ–ļ.        ‚ÜĒ ‚ÜĒ      . –í—ā–ĺ—Ä–ĺ–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ —Ā –Ņ–ĺ–Ľ–ĺ–≤–ł–Ĺ–Ĺ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ķ–Ļ, [3,4,1+,4]: . –í—ā–ĺ—Ä–ĺ–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ —Ā –Ņ–ĺ–Ľ–ĺ–≤–ł–Ĺ–Ĺ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ķ–Ļ, [3,4,1+,4]:        ‚ÜĒ ‚ÜĒ      . –Ď–ĺ–Ľ–Ķ–Ķ –≤—č—Ā–ĺ–ļ–ł–Ļ –ł–Ĺ–ī–Ķ–ļ—Ā —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł, [3,4,4*], –ł–Ĺ–ī–Ķ–ļ—Ā 8, —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā —Ā –Ņ–ł—Ä–į–ľ–ł–ī–į–Ľ—Ć–Ĺ–ĺ–Ļ —Ą—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ—Ć–Ĺ–ĺ–Ļ –ĺ–Ī–Ľ–į—Ā—ā—Ć—é, [((3,‚ąě,3)),((3,‚ąě,3))]: . –Ď–ĺ–Ľ–Ķ–Ķ –≤—č—Ā–ĺ–ļ–ł–Ļ –ł–Ĺ–ī–Ķ–ļ—Ā —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł, [3,4,4*], –ł–Ĺ–ī–Ķ–ļ—Ā 8, —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā —Ā –Ņ–ł—Ä–į–ľ–ł–ī–į–Ľ—Ć–Ĺ–ĺ–Ļ —Ą—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ—Ć–Ĺ–ĺ–Ļ –ĺ–Ī–Ľ–į—Ā—ā—Ć—é, [((3,‚ąě,3)),((3,‚ąě,3))]:      . .
–≠—ā–ł —Ā–ĺ—ā—č —Ā–ĺ–ī–Ķ—Ä–∂–į—ā    , ,      , –ļ–ĺ—ā–ĺ—Ä—č–Ķ –∑–į–ľ–Ķ—Č–į—é—ā 2-–≥–ł–Ņ–Ķ—Ä—Ü–ł–ļ–Ľ–ł—á–Ķ—Ā–ļ–ł–Ķ –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –Ĺ–į–Ņ–ĺ–ī–ĺ–Ī–ł–Ķ –Ņ–į—Ä–į–ļ–ĺ–ľ–Ņ–į–ļ—ā–Ĺ—č—Ö –ľ–ĺ–∑–į–ł–ļ , –ļ–ĺ—ā–ĺ—Ä—č–Ķ –∑–į–ľ–Ķ—Č–į—é—ā 2-–≥–ł–Ņ–Ķ—Ä—Ü–ł–ļ–Ľ–ł—á–Ķ—Ā–ļ–ł–Ķ –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–ł –Ĺ–į–Ņ–ĺ–ī–ĺ–Ī–ł–Ķ –Ņ–į—Ä–į–ļ–ĺ–ľ–Ņ–į–ļ—ā–Ĺ—č—Ö –ľ–ĺ–∑–į–ł–ļ     –ł–Ľ–ł –ł–Ľ–ł     

–°–≤—Ź–∑–į–Ĺ–Ĺ—č–Ķ –ľ–Ĺ–ĺ–≥–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–ł –ł —Ā–ĺ—ā—č
–ú–Ĺ–ĺ–≥–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ –≤—Ö–ĺ–ī–ł—ā –≤ 15 –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ—č—Ö –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–ł—á–Ķ—Ā–ļ–ł—Ö —Ā–ĺ—ā –≤ 3-–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ, 11 –ł–∑ –ļ–ĺ—ā–ĺ—Ä—č—Ö, –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ĺ —ć—ā–ł–ľ —Ā–ĺ—ā–į–ľ, –Ņ–į—Ä–į–ļ–ĺ–ľ–Ņ–į–ļ—ā–Ĺ—č –ł –ł–ľ–Ķ—é—ā –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ—č–Ķ —Ź—á–Ķ–Ļ–ļ–ł –ł–Ľ–ł –≤–Ķ—Ä—ą–ł–Ĺ–Ĺ—č–Ķ —Ą–ł–≥—É—Ä—č.
| 11 –Ņ–į—Ä–į–ļ–ĺ–ľ–Ņ–į–ļ—ā–Ĺ—č—Ö –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ—č—Ö —Ā–ĺ—ā
|

{6,3,3}
|

{6,3,4}
|

{6,3,5}
|

{6,3,6}
|

{4,4,3}
|

{4,4,4}
|

{3,3,6}
|

{4,3,6}
|

{5,3,6}
|

{3,6,3}
|

{3,4,4}
|
–ė–ľ–Ķ–Ķ—ā—Ā—Ź –Ņ—Ź—ā–Ĺ–į–ī—Ü–į—ā—Ć –ĺ–ī–Ĺ–ĺ—Ä–ĺ–ī–Ĺ—č—Ö —Ā–ĺ—ā[–į–Ĺ–≥–Ľ.] –≤ [4,4,3] —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–Ķ –≥—Ä—É–Ņ–Ņ –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į, –≤–ļ–Ľ—é—á–į—Ź —ć—ā—É –ĺ–ī–Ĺ–ĺ—Ä–ĺ–ī–Ĺ—É—é —Ą–ĺ—Ä–ľ—É.
–°–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–ĺ —Ā–ĺ—ā [4,4,3]
{4,4,3}
      
|
r{4,4,3}
      
|
t{4,4,3}
      
|
rr{4,4,3}
      
|
t0,3{4,4,3}
      
|
tr{4,4,3}
      
|
t0,1,3{4,4,3}
      
|
t0,1,2,3{4,4,3}
      
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
{3,4,4}
      
|
r{3,4,4}
      
|
t{3,4,4}
      
|
rr{3,4,4}
      
|
2t{3,4,4}
      
|
tr{3,4,4}
      
|
t0,1,3{3,4,4}
      
|
t0,1,2,3{3,4,4}
      
|
–°–ĺ—ā—č —Ź–≤–Ľ—Ź—é—ā—Ā—Ź —á–į—Ā—ā—Ć—é –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł —Ā–ĺ—ā —Ā –≤–Ķ—Ä—ą–ł–Ĺ–Ĺ–ĺ–Ļ —Ą–ł–≥—É—Ä–ĺ–Ļ –≤ –≤–ł–ī–Ķ –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ–≥–ĺ –Ņ–į—Ä–ļ–Ķ—ā–į:
| –°–ĺ—ā—č {p,4,4}
|
| –ü—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ
|
E3
|
H3
|
| –§–ĺ—Ä–ľ–į
|
–ź—Ą—Ą–ł–Ĺ–Ĺ—č–Ķ
|
–ü–į—Ä–į–ļ–ĺ–ľ–Ņ–į–ļ—ā–Ĺ—č–Ķ
|
–Ě–Ķ–ļ–ľ–Ņ–į–ļ—ā–Ĺ—č–Ķ
|
| –Ě–į–∑–≤–į–Ĺ–ł–Ķ
|
{2,4,4}
|
{3,4,4}
|
{4,4,4}
|
{5,4,4}
|
{6,4,4}
|
..{‚ąě,4,4}
|
Coxeter
      
      
      
|
      
    
    
    
|
      
    
    
|
      
    
    
    
|
      
    
    
|
      
    
    
    
|
      
    
    
    
|
| Image
|

|

|

|

|

|

|
| Cells
|

{2,4}
    
|

{3,4}
    
|

{4,4}
    
|

{5,4}
    
|

{6,4}
    
|

{‚ąě,4}
    
|
–°–ĺ—ā—č —Ź–≤–Ľ—Ź—é—ā—Ā—Ź —á–į—Ā—ā—Ć—é –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ—č—Ö —á–Ķ—ā—č—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ—č—Ö –ľ–Ĺ–ĺ–≥–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–ĺ–≤ –ł —Ā–ĺ—ā —Ā –ĺ–ļ—ā–į—ć–ī—Ä–į–Ľ—Ć–Ĺ—č–ľ–ł —Ź—á–Ķ–Ļ–ļ–į–ľ–ł[–į–Ĺ–≥–Ľ.].
| –ú–Ĺ–ĺ–≥–ĺ–≥—Ä–į–Ĺ–Ĺ–ł–ļ–ł {3,4,p}
|
| –ü—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ
|
S3
|
H3
|
| –§–ĺ—Ä–ľ–į
|
–ö–ĺ–Ĺ–Ķ—á–Ĺ—č–Ķ
|
–ü–į—Ä–į–ļ–ĺ–ľ–Ņ–į–ļ—ā–Ĺ—č–Ķ
|
–Ě–Ķ–ļ–ĺ–ľ–Ņ–į–ļ—ā–Ĺ—č–Ķ
|
| –Ě–į–∑–≤–į–Ĺ–ł–Ķ
|
{3,4,3}
      
   
|
{3,4,4}
      
    
    
|
{3,4,5}
      
|
{3,4,6}
      
    
|
{3,4,7}
      
|
{3,4,8}
      
     
|
... {3,4,‚ąě}
      
     
|
| –†–ł—Ā—É–Ĺ–ĺ–ļ
|

|

|

|

|

|

|

|
Vertex
figure
|

{4,3}
    
  
|

{4,4}
    
  
  
|

{4,5}
    
|

{4,6}
    
  
|

{4,7}
    
|

{4,8}
    
   
|

{4,‚ąě}
    
   
|
–°–Ņ—Ä—Ź–ľ–Ľ—Ď–Ĺ–Ĺ—č–Ķ –≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ —Ā–ĺ—ā—č –Ņ–ĺ—Ä—Ź–ī–ļ–į 4
–°–Ņ—Ä—Ź–ľ–Ľ—Ď–Ĺ–Ĺ—č–Ķ –≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ —Ā–ĺ—ā—č –Ņ–ĺ—Ä—Ź–ī–ļ–į 4, t1{3,4,4},        –ł–ľ–Ķ—é—ā —Ą–į—Ā–Ķ—ā—č –≤ –≤–ł–ī–Ķ –ļ—É–Ī–ĺ–ĺ–ļ—ā–į—ć–ī—Ä–į –ł –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ–≥–ĺ –Ņ–į—Ä–ļ–Ķ—ā–į, —Ā –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ–Ļ –Ņ–ł—Ä–į–ľ–ł–ī–ĺ–Ļ –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ –≤–Ķ—Ä—ą–ł–Ĺ–Ĺ–ĺ–Ļ —Ą–ł–≥—É—Ä—č. –ł–ľ–Ķ—é—ā —Ą–į—Ā–Ķ—ā—č –≤ –≤–ł–ī–Ķ –ļ—É–Ī–ĺ–ĺ–ļ—ā–į—ć–ī—Ä–į –ł –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ–≥–ĺ –Ņ–į—Ä–ļ–Ķ—ā–į, —Ā –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ–Ļ –Ņ–ł—Ä–į–ľ–ł–ī–ĺ–Ļ –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ –≤–Ķ—Ä—ą–ł–Ĺ–Ĺ–ĺ–Ļ —Ą–ł–≥—É—Ä—č.
–£—Ā–Ķ—á—Ď–Ĺ–Ĺ—č–Ķ –≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ —Ā–ĺ—ā—č –Ņ–ĺ—Ä—Ź–ī–ļ–į 4
–£—Ā–Ķ—á—Ď–Ĺ–Ĺ—č–Ķ –≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ —Ā–ĺ—ā—č –Ņ–ĺ—Ä—Ź–ī–ļ–į 4, t0,1{3,4,4},        –ł–ľ–Ķ—é—ā —Ą–į—Ā–Ķ—ā—č –≤ –≤–ł–ī–Ķ —É—Ā–Ķ—á—Ď–Ĺ–Ĺ–ĺ–≥–ĺ –ĺ–ļ—ā–į—ć–ī—Ä–į –ł –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ–≥–ĺ –Ņ–į—Ä–ļ–Ķ—ā–į —Ā –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ–Ļ –Ņ–ł—Ä–į–ľ–ł–ī–ĺ–Ļ –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ –≤–Ķ—Ä—ą–ł–Ĺ–Ĺ–ĺ–Ļ —Ą–ł–≥—É—Ä—č. –ł–ľ–Ķ—é—ā —Ą–į—Ā–Ķ—ā—č –≤ –≤–ł–ī–Ķ —É—Ā–Ķ—á—Ď–Ĺ–Ĺ–ĺ–≥–ĺ –ĺ–ļ—ā–į—ć–ī—Ä–į –ł –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ–≥–ĺ –Ņ–į—Ä–ļ–Ķ—ā–į —Ā –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ–Ļ –Ņ–ł—Ä–į–ľ–ł–ī–ĺ–Ļ –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ –≤–Ķ—Ä—ą–ł–Ĺ–Ĺ–ĺ–Ļ —Ą–ł–≥—É—Ä—č.
–°–ļ–ĺ—ą–Ķ–Ĺ–Ĺ—č–Ķ –≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ —Ā–ĺ—ā—č –Ņ–ĺ—Ä—Ź–ī–ļ–į 4
| –°–ļ–ĺ—ą–Ķ–Ĺ–Ĺ—č–Ķ –≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ —Ā–ĺ—ā—č –Ņ–ĺ—Ä—Ź–ī–ļ–į 4
|
| –Ę–ł–Ņ |
–ü–į—Ä–į–ļ–ĺ–ľ–Ņ–į–ļ—ā–Ĺ—č–Ķ –ĺ–ī–Ĺ–ĺ—Ä–ĺ–ī–Ĺ—č–Ķ —Ā–ĺ—ā—č[–į–Ĺ–≥–Ľ.]
|
| –°–ł–ľ–≤–ĺ–Ľ—č –®–Ľ–Ķ—Ą–Ľ–ł |
rr{3,4,4} –ł–Ľ–ł t0,2{3,4,4}
s2{3,4,4}
|
–Ē–ł–į–≥—Ä–į–ľ–ľ—č
–ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į ‚ÄĒ –Ē—č–Ĺ–ļ–ł–Ĺ–į |
      
      
     ‚ÜĒ ‚ÜĒ       
|
| –Į—á–Ķ–Ļ–ļ–ł |
rr{3,4} 
r{4,4}
|
| –ď—Ä–į–Ĺ–ł |
—ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ {3}
–ļ–≤–į–ī—Ä–į—ā {4}
|
| –í–Ķ—Ä—ą–ł–Ĺ–Ĺ–į—Ź —Ą–ł–≥—É—Ä–į |

—ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–į—Ź –Ņ—Ä–ł–∑–ľ–į
|
| –ď—Ä—É–Ņ–Ņ—č –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į |
[4,4,3]
|
| –°–≤–ĺ–Ļ—Ā—ā–≤–į |
–≤–Ķ—Ä—ą–ł–Ĺ–Ĺ–ĺ —ā—Ä–į–Ĺ–∑–ł—ā–ł–≤–Ĺ—č
|
–°–ļ–ĺ—ą–Ķ–Ĺ–Ĺ—č–Ķ –≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ —Ā–ĺ—ā—č –Ņ–ĺ—Ä—Ź–ī–ļ–į 4, t0,2{3,4,4},        –ł–ľ–Ķ—é—ā –≥—Ä–į–Ĺ–ł –≤ –≤–ł–ī–Ķ —Ä–ĺ–ľ–Ī–ĺ–ļ—É–Ī–ĺ–ĺ–ļ—ā–į—ć–ī—Ä–į –ł –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ–≥–ĺ –Ņ–į—Ä–ļ–Ķ—ā–į —Ā –≤–Ķ—Ä—ą–ł–Ĺ–Ĺ–ĺ–Ļ —Ą–ł–≥—É—Ä–ĺ–Ļ –≤ –≤–ł–ī–Ķ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ—Ä–ł–∑–ľ—č. –ł–ľ–Ķ—é—ā –≥—Ä–į–Ĺ–ł –≤ –≤–ł–ī–Ķ —Ä–ĺ–ľ–Ī–ĺ–ļ—É–Ī–ĺ–ĺ–ļ—ā–į—ć–ī—Ä–į –ł –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ–≥–ĺ –Ņ–į—Ä–ļ–Ķ—ā–į —Ā –≤–Ķ—Ä—ą–ł–Ĺ–Ĺ–ĺ–Ļ —Ą–ł–≥—É—Ä–ĺ–Ļ –≤ –≤–ł–ī–Ķ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ—Ä–ł–∑–ľ—č.
–°–ļ–ĺ—ą–Ķ–Ĺ–ĺ-—É—Ā–Ķ—á—Ď–Ĺ–Ĺ—č–Ķ –≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ —Ā–ĺ—ā—č –Ņ–ĺ—Ä—Ź–ī–ļ–į 4
| –°–ļ–ĺ—ą–Ķ–Ĺ–ĺ-—É—Ā–Ķ—á—Ď–Ĺ–Ĺ—č–Ķ –≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ —Ā–ĺ—ā—č –Ņ–ĺ—Ä—Ź–ī–ļ–į 4
|
| –Ę–ł–Ņ |
–ü–į—Ä–į–ļ–ĺ–ľ–Ņ–į–ļ—ā–Ĺ—č–Ķ –ĺ–ī–Ĺ–ĺ—Ä–ĺ–ī–Ĺ—č–Ķ —Ā–ĺ—ā—č[–į–Ĺ–≥–Ľ.]
|
| –°–ł–ľ–≤–ĺ–Ľ—č –®–Ľ–Ķ—Ą–Ľ–ł |
tr{3,4,4} –ł–Ľ–ł t0,1,2{3,4,4}
|
–Ē–ł–į–≥—Ä–į–ľ–ľ—č
–ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į ‚ÄĒ –Ē—č–Ĺ–ļ–ł–Ĺ–į |
      
     ‚ÜĒ ‚ÜĒ       
|
| –Į—á–Ķ–Ļ–ļ–ł |
tr{3,4} 
r{4,4}
|
| –ď—Ä–į–Ĺ–ł |
–ļ–≤–į–ī—Ä–į—ā–Ĺ—č–Ķ {4}
—ą–Ķ—Ā—ā–ł—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ {6}
–≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ {8}
|
| –í–Ķ—Ä—ą–ł–Ĺ–Ĺ–į—Ź —Ą–ł–≥—É—Ä–į |
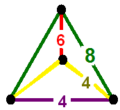
—ā–Ķ—ā—Ä–į—ć–ī—Ä
|
| –ď—Ä—É–Ņ–Ņ—č –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į |
[4,4,3]
|
| –°–≤–ĺ–Ļ—Ā—ā–≤–į |
–≤–Ķ—Ä—ą–ł–Ĺ–Ĺ–ĺ —ā—Ä–į–Ĺ–∑–ł—ā–ł–≤–Ĺ—č
|
–°–ļ–ĺ—ą–Ķ–Ĺ–ĺ-—É—Ā–Ķ—á—Ď–Ĺ–Ĺ—č–Ķ –≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ —Ā–ĺ—ā—č –Ņ–ĺ—Ä—Ź–ī–ļ–į 4, t0,1,2{3,4,4},        –ł–ľ–Ķ—é—ā —Ą–į—Ā–Ķ—ā—č –≤ –≤–ł–ī–Ķ —É—Ā–Ķ—á—Ď–Ĺ–Ĺ–ĺ–≥–ĺ –ļ—É–Ī–ĺ–ĺ–ļ—ā–į—ć–ī—Ä–į –ł –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ–≥–ĺ –Ņ–į—Ä–ļ–Ķ—ā–į —Ā —ā–Ķ—ā—Ä–į—ć–ī—Ä–ĺ–ľ –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ –≤–Ķ—Ä—ą–ł–Ĺ–Ĺ–ĺ–Ļ —Ą–ł–≥—É—Ä—č. –ł–ľ–Ķ—é—ā —Ą–į—Ā–Ķ—ā—č –≤ –≤–ł–ī–Ķ —É—Ā–Ķ—á—Ď–Ĺ–Ĺ–ĺ–≥–ĺ –ļ—É–Ī–ĺ–ĺ–ļ—ā–į—ć–ī—Ä–į –ł –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ–≥–ĺ –Ņ–į—Ä–ļ–Ķ—ā–į —Ā —ā–Ķ—ā—Ä–į—ć–ī—Ä–ĺ–ľ –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ –≤–Ķ—Ä—ą–ł–Ĺ–Ĺ–ĺ–Ļ —Ą–ł–≥—É—Ä—č.
–°—ā—Ä—É–≥-—É—Ā–Ķ—á—Ď–Ĺ–Ĺ—č–Ķ –≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ —Ā–ĺ—ā—č –Ņ–ĺ—Ä—Ź–ī–ļ–į 4
–°—ā—Ä—É–≥-—É—Ā–Ķ—á—Ď–Ĺ–Ĺ—č–Ķ –≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ —Ā–ĺ—ā—č –Ņ–ĺ—Ä—Ź–ī–ļ–į 4, t0,1,3{3,4,4},        –ł–ľ–Ķ—é—ā —Ą–į—Ā–Ķ—ā—č –≤ –≤–ł–ī–Ķ —É—Ā–Ķ—á—Ď–Ĺ–Ĺ–ĺ–≥–ĺ –ĺ–ļ—ā–į—ć–ī—Ä–į –ł –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ–≥–ĺ –Ņ–į—Ä–ļ–Ķ—ā–į —Ā –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ–Ļ –Ņ–ł—Ä–į–ľ–ł–ī–ĺ–Ļ –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ –≤–Ķ—Ä—ą–ł–Ĺ–Ĺ–ĺ–Ļ —Ą–ł–≥—É—Ä—č. –ł–ľ–Ķ—é—ā —Ą–į—Ā–Ķ—ā—č –≤ –≤–ł–ī–Ķ —É—Ā–Ķ—á—Ď–Ĺ–Ĺ–ĺ–≥–ĺ –ĺ–ļ—ā–į—ć–ī—Ä–į –ł –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ–≥–ĺ –Ņ–į—Ä–ļ–Ķ—ā–į —Ā –ļ–≤–į–ī—Ä–į—ā–Ĺ–ĺ–Ļ –Ņ–ł—Ä–į–ľ–ł–ī–ĺ–Ļ –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ –≤–Ķ—Ä—ą–ł–Ĺ–Ĺ–ĺ–Ļ —Ą–ł–≥—É—Ä—č.
–ü–Ľ–ĺ—Ā–ļ–ĺ–Ĺ–ĺ—Ā—č–Ķ –≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ —Ā–ĺ—ā—č –Ņ–ĺ—Ä—Ź–ī–ļ–į 4
–ü–Ľ–ĺ—Ā–ļ–ĺ–Ĺ–ĺ—Ā—č–Ķ –≤–ĺ—Ā—Ć–ľ–ł—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ķ —Ā–ĺ—ā—č –Ņ–ĺ—Ä—Ź–ī–ļ–į 4, s{3,4,4}, –ł–ľ–Ķ—é—ā –ī–ł–į–≥—Ä–į–ľ–ľ—É –ö–ĺ–ļ—Ā–Ķ—ā–Ķ—Ä–į ‚ÄĒ –Ē—č–Ĺ–ļ–ł–Ĺ–į        . –ě–Ĺ–ł —Ź–≤–Ľ—Ź—é—ā—Ā—Ź —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ—č–ľ–ł —Ā–ĺ—ā–į–ľ–ł[–į–Ĺ–≥–Ľ.] —Ā –ļ–≤–į–ī—Ä–į—ā–Ĺ—č–ľ–ł –Ņ–ł—Ä–į–ľ–ł–ī–į–ľ–ł, –ļ–≤–į–ī—Ä–į—ā–Ĺ—č–ľ–ł –ľ–ĺ–∑–į–ł–ļ–į–ľ–ł –ł –ł–ļ–ĺ—Ā–į—ć–ī—Ä–į–ľ–ł. . –ě–Ĺ–ł —Ź–≤–Ľ—Ź—é—ā—Ā—Ź —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ—č–ľ–ł —Ā–ĺ—ā–į–ľ–ł[–į–Ĺ–≥–Ľ.] —Ā –ļ–≤–į–ī—Ä–į—ā–Ĺ—č–ľ–ł –Ņ–ł—Ä–į–ľ–ł–ī–į–ľ–ł, –ļ–≤–į–ī—Ä–į—ā–Ĺ—č–ľ–ł –ľ–ĺ–∑–į–ł–ļ–į–ľ–ł –ł –ł–ļ–ĺ—Ā–į—ć–ī—Ä–į–ľ–ł.
–°–ľ. —ā–į–ļ–∂–Ķ
–ü—Ä–ł–ľ–Ķ—á–į–Ĺ–ł—Ź
–õ–ł—ā–Ķ—Ä–į—ā—É—Ä–į
- Coxeter. Tables I and II: Regular polytopes and honeycombs // Regular Polytopes[–į–Ĺ–≥–Ľ.]. ‚ÄĒ 3rd. ed.. ‚ÄĒ Dover Publications, 1973. ‚ÄĒ –°. 294‚Äď296. ‚ÄĒ ISBN 0-486-61480-8.
- Coxeter. Chapter 10: Regular honeycombs in hyperbolic space, Summary tables II,III,IV,V // The Beauty of Geometry: Twelve Essays. ‚ÄĒ Dover Publications, 1999. ‚ÄĒ –°. 212-213. ‚ÄĒ ISBN 0-486-40919-8.
- Jeffrey R. Weeks. Chapter 16-17: Geometries on Three-manifolds I,II // The Shape of Space. ‚ÄĒ 2nd. ‚ÄĒ 2002. ‚ÄĒ ISBN 0-8247-0709-5.
- N.W. Johnson. Uniform Polytopes. ‚ÄĒ (Manuscript).
- N.W. Johnson. The Theory of Uniform Polytopes and Honeycombs. ‚ÄĒ University of Toronto, 1966. ‚ÄĒ (Ph.D. Dissertation).
- N.W. Johnson. Chapter 13: Hyperbolic Coxeter groups // Geometries and Transformations. ‚ÄĒ 2015.
- Norman W. Johnson, Asia Ivic Weiss. Quadratic Integers and Coxeter Groups // Can. J. Math.. ‚ÄĒ 1999. ‚ÄĒ –Ę. 51, –≤—č–Ņ. 6. ‚ÄĒ –°. 1307‚Äď1336.
|