| Распределение Бернулли |
|---|
 Функция вероятности Функция вероятности |
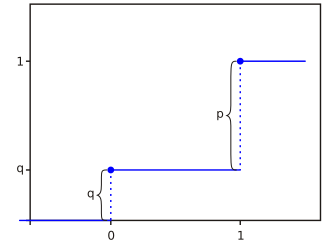 Функция распределения Функция распределения |
| Параметры |

 |
| Носитель |
 |
| Функция вероятности |
 |
| Функция распределения |
 |
| Математическое ожидание |
 |
| Мода |
 |
| Дисперсия |
 |
| Коэффициент асимметрии |
 |
| Коэффициент эксцесса |
 |
| Дифференциальная энтропия |
 |
| Производящая функция моментов |
 |
| Характеристическая функция |
 |
Распределе́ние Берну́лли в теории вероятностей и математической статистике — дискретное распределение вероятностей, моделирующее случайный эксперимент произвольной природы, при заранее известной вероятности успеха или неудачи.
Определение
Случайная величина  имеет распределение Бернулли, если она принимает всего два значения:
имеет распределение Бернулли, если она принимает всего два значения:  и
и  с вероятностями
с вероятностями  и
и  соответственно. Таким образом:
соответственно. Таким образом:
 ,
, .
.
Принято говорить, что событие  соответствует «успеху», а событие
соответствует «успеху», а событие  — «неудаче». Эти названия условные, и в зависимости от конкретной задачи могут быть заменены на противоположные.
— «неудаче». Эти названия условные, и в зависимости от конкретной задачи могут быть заменены на противоположные.
Свойства
Предельное свойство
Предельное свойство описывается теоремой Пуассона:
Пусть есть последовательность серий испытаний Бернулли, где  — вероятность «успеха»,
— вероятность «успеха»,  — количество «успехов».
— количество «успехов».
Тогда если



- то

Моменты распределения Бернулли
![{\displaystyle \mathbb {E} [X]=p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41bff53623cf28729d4da4500f0618fd24380b0b) ,
,![{\displaystyle \operatorname {D} [X]=p(1-p)=pq}](https://wikimedia.org/api/rest_v1/media/math/render/svg/676350236a16d3c5d5d603eaf93da7b006fc3454) , так как:
, так как:  .
.
Вообще, легко видеть, что
![{\displaystyle \mathbb {E} \left[X^{n}\right]=\Pr(X=1)\cdot 1^{n}+\Pr(X=0)\cdot 0^{n}=p\cdot 1^{n}+q\cdot 0^{n}=p=\mathbb {E} [X],\forall n\in \mathbb {N} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9798a45d24eee884b4c9b48c1b79129d8132b4fc)
Замечание
Если независимые случайные величины  , имеют распределение Бернулли с вероятностью успеха
, имеют распределение Бернулли с вероятностью успеха  , то
, то

имеет биномиальное распределение с  степенями свободы.
степенями свободы.
См. также
Литература
- Hazewinkel, Michiel, ed. (2001), "Binomial distribution", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
 |
|---|
| Дискретные | |
|---|
Абсолютно
непрерывные | |
|---|




























![{\displaystyle \mathbb {E} [X]=p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41bff53623cf28729d4da4500f0618fd24380b0b)
![{\displaystyle \operatorname {D} [X]=p(1-p)=pq}](https://wikimedia.org/api/rest_v1/media/math/render/svg/676350236a16d3c5d5d603eaf93da7b006fc3454)

![{\displaystyle \mathbb {E} \left[X^{n}\right]=\Pr(X=1)\cdot 1^{n}+\Pr(X=0)\cdot 0^{n}=p\cdot 1^{n}+q\cdot 0^{n}=p=\mathbb {E} [X],\forall n\in \mathbb {N} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9798a45d24eee884b4c9b48c1b79129d8132b4fc)
















