Сопряжённые функторы

Сопряжённые функторы — пара функторов, состоящих в определённом соотношении между собой. Понятие сопряжённых функторов и сам термин были предложены Даниэлем Каном в 1956 году^[1]. Сопряжённые функторы часто встречаются в разных областях математики.

Функторы F и G сопряжены, если существует естественная биекция ${\displaystyle \mathrm {Hom} (F(X),Y)\simeq \mathrm {Hom} (X,G(Y))}$. Тогда F называется левым сопряжённым функтором, а G — правым.

Сопряжённые функторы — один из ключевых инструментов теории категорий, многие примечательные математические конструкции могут быть описаны как сопряжённые функторы. В результате из общих теорем о сопряжённых функторах, таких как эквивалентность различных определений, и из того факта, что правые сопряжённые функторы коммутируют с пределами (а левые — с копределами), могут немедленно следовать доказательства многих интересных результатов.

Можно сказать, что сопряжённый функтор — это способ указания наиболее эффективного решения некоторой проблемы с помощью стандартного метода. Например, элементарная проблема из теории колец — как превратить псевдокольцо (то есть кольцо, которое может не иметь мультипликативной единицы) в кольцо. Наиболее эффективный способ это сделать — добавить в кольцо единицу, все элементы, необходимые для выполнения аксиом кольца (например, элементы типа r+1, где r — элемент кольца) и не предполагать никаких соотношений в новом кольце, которые не необходимы для выполнения аксиом. Эта конструкция стандартна в том смысле, что она работает для любого псевдокольца.

Приведенное выше описание очень расплывчато, но его можно сделать точным, используя язык теории категорий: конструкция «наиболее эффективна», если она удовлетворяет универсальному свойству, и «стандартна» в том смысле, что она задаёт функтор. Универсальные свойства делятся на начальные и терминальные, так как эти понятия двойственны, достаточно рассмотреть одно из них.

Идея использования начального свойства состоит в том, чтобы сформулировать проблему в терминах такой вспомогательной категории E, чтобы осталось лишь найти начальный объект E. Такая формулировка имеет то преимущество, что задача «нахождения наиболее эффективного решения» становится вполне строгой и в каком-то смысле сходной с задачей нахождения экстремума. Для выбора правильной категории E иногда требуется подбирать непростые приёмы: в случае полукольца R нужная категория — это категория, объекты которой — гомоморфизмы полуколец R → S, где S — некоторое кольцо с единицей. Морфизмы в E между R → S₁ и R → S₂ — коммутативные треугольники вида (R → S₁,R → S₂, S₁ → S₂), где S₁ → S₂ — гомоморфизм колец. Существование морфизма между R → S₁ и R → S₂ означает, что S₁ — не менее эффективное решение проблемы, чем S₂: S₂ имеет больше добавленных элементов и (или) больше соотношений между ними, чем S₁.

Сказать, что этот метод определяет «наиболее эффективное» и «стандартное» решение проблемы — то же самое, что сказать, что он задает сопряжённые функторы.

Существуют несколько эквивалентных определений сопряжённых функторов. Их эквивалентность элементарна, но не тривиальна.

Определение с помощью универсальной стрелки➤ легко сформулировать, оно также наиболее близко к нашей интуиции по поводу «оптимизационной задачи».

Определение с помощью единицы и коединицы➤ удобно для функторов, часто встречающихся в алгебре, потому что предоставляет формулы, которые можно проверить напрямую.

Определение с помощью множеств Hom➤ делает очевидной симметричность определения и проясняет причины для именования функторов «сопряжёнными».

Функтор F : C ← D — левый сопряжённый функтор, если для каждого объекта X категории C существует терминальная стрелка ε_X из F в X. Если для каждого X в C мы выберем объект G₀X в D, для которого определена терминальная стрелка ε_X : F(G₀X) → X, то существует единственный функтор G : C → D, такой, что GX = G₀X и для любого морфизма в категории C f : X → Xʹ выполняется ε_Xʹ ∘ FG(f) = f ∘ ε_X; F тогда называют левым сопряжённым к функтору G.

Функтор G : C → D — правый сопряжённый функтор, если для каждого объекта Y категории D существует начальная стрелка из Y в G. Если для каждого Y в D выбрать объект F₀Y в C, такой, что определена начальная стрелка η_Y : Y → G(F₀Y) из Y в G, то существует единственный функтор F : C ← D, такой, что FY = F₀Y и GF(g) ∘ η_Y = η_Yʹ ∘ g для g : Y → Yʹ — морфизма в D; G тогда называют правым сопряжённым к функтору F.

Как и подразумевает терминология, верно, что F — левый сопряжённый для G тогда и только тогда, когда G — правый сопряжённый для F. Однако это не очевидно из определения через универсальную стрелку, но очевидно благодаря определению через единицу и коединицу.

Для задания единицы и коединицы в категориях C и D нужно зафиксировать два функтора F : C ← D, G : C → D и два естественных преобразования:

${\displaystyle {\begin{aligned}\varepsilon &:FG\to 1_{\mathcal {C}}\\\eta &:1_{\mathcal {D}}\to GF\end{aligned}}}$,

называемых соответственно коединицей и единицей сопряжения, таких, что композиции

${\displaystyle F{\xrightarrow {\;F\eta \;}}FGF{\xrightarrow {\;\varepsilon F\,}}F}$ и

${\displaystyle G{\xrightarrow {\;\eta G\;}}GFG{\xrightarrow {\;G\varepsilon \,}}G}$

являются тождественными преобразованиями 1_F и 1_G функторов F и G соответственно.

В такой ситуации F является левым сопряжённым для G и G является правым сопряжённым для F. Иногда это отношение обозначают ${\displaystyle (\varepsilon ,\eta ):F\dashv G}$ или просто ${\displaystyle F\dashv G}$ .

В форме уравнений приведённые выше условия на (ε,η) называются уравнениями коединицы и единицы:

${\displaystyle {\begin{aligned}1_{F}&=\varepsilon F\circ F\eta \\1_{G}&=G\varepsilon \circ \eta G\end{aligned}}}$

Рассмотрим два функтора F : C ← D и G : C → D. Пусть существует естественный изоморфизм:

${\displaystyle \Phi :\mathrm {hom} _{C}(F-,-)\to \mathrm {hom} _{D}(-,G-)}$.

Это определяет семейство биекций:

${\displaystyle \Phi _{Y,X}:\mathrm {hom} _{C}(FY,X)\to \mathrm {hom} _{D}(Y,GX)}$.

для всех объектов X в C и Y в D.

Здесь F называется левым сопряжённым для G и G — правым сопряжённым для F.

Чтобы понять, что подразумевается под естественностью Φ, нужно объяснить, каким образом hom_C(F-, -) и hom_D(-, G-) являются функторами. На самом деле, они оба являются бифункторами из D^op × C в Set. В явном виде естественность Φ означает, что для всех морфизмов f : X → X′ в C и морфизмов g : Y ′ → Y в D следующая диаграмма коммутирует: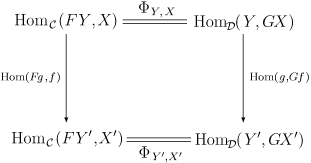

Конструкция свободной группы является удобным примером для прояснения сути определений. Пусть F : Grp ← Set — функтор, который множеству Y сопоставляет свободную группу, порожденную элементами Y, и G : Grp → Set — забывающий функтор, сопоставляющий группе X её множество-носитель. Тогда F — левый сопряжённый для G:

Терминальные стрелки: для каждой группы X, группа FGX — свободная группа, порождённая элементами X как множеством. Пусть ${\displaystyle \varepsilon _{X}:FGX\to X}$ — гомоморфизм групп, который переводит образующие FGX в соответствующие элементы X. Тогда ${\displaystyle (GX,\varepsilon _{X})}$ — терминальный морфизм из F в X, потому что любой гомоморфизм из свободной группы FZ в X проносится через ${\displaystyle \varepsilon _{X}:FGX\to X}$ при помощи единственной функции из множества Z во множество X. Это означает, что (F,G) — пара сопряжённых функторов.

Множества Hom: отображения из свободной группы FY в группу X однозначно соответствуют отображениям множества Y во множество GX: каждый гомоморфизм однозначно определяется своими значениями на образующих свободной группы. Прямым вычислением можно проверить, что это соответствие — естественное преобразование, а значит, пара (F,G) сопряжённая.

• Все свободные объекты^[англ.] — результаты применения свободного функтора, который является левым сопряжённым для забывающего функтора.
• Произведения, ядра и уравнители — примеры категорных пределов. Все функторы предела являются правыми сопряжёнными к диагональному функтору. Аналогично, копроизведения, коядра и коуравнители являются копределами, а функтор копредела — левый сопряжённый для диагонального.
• Добавление единицы в псевдокольцо (пример из раздела «Мотивировка»). Если нам дано псевдокольцо R, то соответствующее ему кольцо — это произведение R × Z, на котором определено Z-билинейное произведение по формуле (r,0)(0,1) = (0,1)(r,0) = (r,0), (r,0)(s,0) = (rs,0), (0,1)(0,1) = (0,1). Построенный функтор сопряжён слева к забывающему функтору, отправляющему кольцо в соответствующее ему псевдокольцо.
• Расширения колец. Пусть R и S — кольца, и ρ : R → S — гомоморфизм колец. Тогда S можно рассматривать как (левый) R-модуль, и тензорное произведение с S определяет функтор F : R-Mod → S-Mod. Здесь F сопряжён слева к забывающему функтору G : S-Mod → R-Mod.
• Тензорные произведения. Если R — кольцо и M — правый R-модуль, то тензорное произведение с M определяет функтор F : R-Mod → Ab. Функтор G : Ab → R-Mod, определенный как G(A) = hom_Z(M,A) сопряжён справа к F.
• Поле частных. Для категории Dom_m целостных колец и инъективных гомоморфизмов, забывающий функтор Field → Dom_m имеет левый сопряжённый, сопоставляющий каждому целостному кольцу его поле частных.
• Кольца многочленов'. Для Ring_* — категории коммутативных колец с отмеченным элементом и гомоморфизмов, сохраняющих отмеченный элемент, забывающий функтор G:Ring_* → Ring имеет левый сопряжённый — он сопоставляет кольцу R пару (R[x], x), где R[x] — кольцо многочленов с коэффициентами из R.
• Абелианизация. Забывающий функтор G : Ab → Grp имеет левый сопряжённый, называемый функтором абелианизации, который каждой группе G сопоставляет факторгруппу по коммутанту: G^ab = G/[G,G].

• Функтор с двумя сопряжёнными. Пусть G — функтор, сопоставляющий топологическому пространству его множество-носитель (то есть забывающий топологию). У G есть левый сопряжённый F, наделяющий множества дискретной топологией, и правый сопряжённый H, наделяющий множества тривиальной топологией.
• Надстройка и пространства петель. По данным топологическим пространствам X и Y можно построить пространство [SX, Y] классов гомотопии отображений из надстройки SX в Y. Оно естественным образом изоморфно пространству [X, ΩY] классов гомотопии отображений из X в пространство петель ΩY, поэтому функторы надстройки и пространства петель сопряжены в гомотопической категории топологических пространств.
• Вложение G : KHaus → Top категории компактных хаусдорфовых пространств в категорию топологических пространств имеет левый сопряжённый функтор F : Top → KHaus — компактификацию Стоуна — Чеха. Коединица этой пары задаёт непрерывное отображение из произвольного топологического пространства X в его компактификацию. Это отображение является вложением тогда и только тогда, когда X — вполне регулярное пространство.

Не каждый функтор G : C → D имеет левый или правый сопряжённый. Если C — полная категория, то по теореме о сопряжённых функторах Петера Фрейда G имеет левый сопряжённый тогда и только тогда, когда для любого Y из категории D существует семейство морфизмов:

f_i : Y → G(X_i),

где индексы i пробегают множество I, такое, что любой морфизм:

h : Y → G(X)

может быть записан как:

h = G(t) o f_i

для некоторого i в I и некоторого морфизма:

t : X_i → X в C.

Аналогичное утверждение характеризует функторы, имеющие правый сопряжённый.

Если функтор F : C ← D имеет два правых сопряжённых G и G′, то G и G′ естественно изоморфны.

В другую сторону, если F сопряжён слева к G, и G естественно изоморфен G′, то F также сопряжён слева к G′.

Композиции сопряжений можно брать естественным образом. Если 〈F, G, ε, η〉 — сопряжение между C и D, и 〈F′, G′, ε′, η′〉 — сопряжение между D и E, то функтор

${\displaystyle F'\circ F:{\mathcal {C}}\leftarrow {\mathcal {E}}}$

сопряжён слева к функтору

${\displaystyle G\circ G':{\mathcal {C}}\to {\mathcal {E}}}$.

Можно образовать категорию, объекты которой — все малые категории, а морфизмы — сопряжения.

Наиболее важное свойство сопряжённых функторов — их непрерывность: каждый функтор, имеющий левый сопряжённый (то есть являющийся правым сопряжённым), коммутирует с пределами в категорном смысле. Соответственно, функтор, имеющий правый сопряжённый, конепрерывен, то есть коммутирует с копределами. Поскольку многие конструкции являются пределами или копределами, из этого сразу вытекает несколько следствий. Например:

• Применение правого сопряжённого функтора к произведению даёт произведение образов.
• Применение левого сопряжённого функтора к копроизведению даёт копроизведение образов.
• Каждый правый сопряжённый и аддитивный функтор между абелевыми категориями точен слева.
• Каждый левый сопряжённый и аддитивный функтор между абелевыми категориями точен справа.

• Маклейн С. Глава 4. Сопряжённые функторы // Категории для работающего математика = Categories for the working mathematician / Пер. с англ. под ред. В. А. Артамонова. — М.: Физматлит, 2004. — С. 95—128. — 352 с. — ISBN 5-9221-0400-4.

• F. Borceux. Handbook of Categorical Algebra 1. Basic Category Theory. — Encyclopaedia of Mathematics and its Applications. — Cambridge: Cambridge University Press, 1994. — 345 p. — ISBN 0 521 44178 1.
• Adámek, Jiří; Herrlich, Horst; Strecker, George E. Abstract and Concrete Categories. The joy of cats (англ.). — John Wiley & Sons, 1990. — ISBN 0-471-60922-6.