Дискретна Фуријеова трансформација

Дискретна Фуријеова трансформација или ДФТ јесте Фуријеова трансформација дискретног и коначног (или периодичног) сигнала. Дискретна Фуријеова трансформација је тиме и специјални облик Z-трансформације код које се z налази на јединичном кругу. Често се користи при обради дигиталних сигнала, а најпознатији алгоритам за то је брза фуријеова трансформација (FFT, Fast Fourier Transformation, енгл.).

Дискретна Фуријеова трансформација може да послужи такође за апроксимацију (у одређеним случајевима и реконструкцију) функције која одговара сигналу или као имплементација дигиталних филтера.

Путем инверзне Фуријеове трансформације се из Фуријеових коефицијената склапа излазни сигнал, а повезивањем ДФТ и инверзне ДФТ можемо да манипулишемо фреквенцијама (налази примену при еквилајзерима и филтерима).

Узмимо да је ${\displaystyle R}$ комутативан, унитаран прстен, у којем је број ${\displaystyle N}$ јединица. Даље, у ${\displaystyle R}$ је ${\displaystyle w}$ јединични корен.

За вектор ${\displaystyle c=(c_{0},\dots ,c_{N-1})\in R^{N}}$ је дискретна фуријеова трансформација ${\displaystyle {\hat {c}}}$ на следећи начин дефинисана:

${\displaystyle {\hat {c}}_{k}=\sum _{j=0}^{N-1}w^{\,j\cdot k}\cdot c_{j}}$ за ${\displaystyle k=0,\dots ,N-1}$

А за ${\displaystyle {\hat {c}}_{k}}$, инверзна фуријеова трансформација је

${\displaystyle c_{k}={1 \over N}\sum _{j=0}^{N-1}w^{-j\cdot k}\cdot {\hat {c}}_{j}}$ за ${\displaystyle k=0,\dots ,N-1}$

У комплексном домену користимо ${\displaystyle w=e^{{2*\pi *k} \over n},\quad k=0,1,\ldots ,n-1}$.

Онда је ДФТ за ${\displaystyle c\in {\mathbb {C}}^{N}}$: ${\displaystyle {\hat {c}}_{k}=\sum _{j=0}^{N-1}e^{-2\pi \mathrm {i} \cdot {\frac {jk}{N}}}\cdot c_{j}}$ за ${\displaystyle k=0,\dots ,N-1}$,

а ИДФТ за ${\displaystyle {\hat {c}}\in {\mathbb {C}}^{N}}$: ${\displaystyle c_{k}={\frac {1}{N}}\sum _{j=0}^{N-1}e^{2\pi \mathrm {i} \cdot {\frac {jk}{N}}}\cdot {\hat {c}}_{j}}$ за ${\displaystyle k=0,\dots ,N-1}$

Рачуница у реалном домену је:

${\displaystyle {\hat {c}}_{N-k}=\sum _{j=0}^{N-1}e^{-2\pi \mathrm {i} \cdot {\frac {j(N-k)}{N}}}\cdot c_{j}=\sum _{j=0}^{N-1}e^{-2\pi \mathrm {i} \cdot ({\frac {jN}{N}}-{\frac {k}{N}})}\cdot c_{j}=\sum _{j=0}^{N-1}e^{-2\pi \mathrm {i} \cdot ({\frac {jN}{N}})}e^{2\pi \mathrm {i} \cdot ({\frac {k}{N}})}\cdot c_{j}=\sum _{j=0}^{N-1}e^{-2\pi \mathrm {i} \cdot j}e^{2\pi \mathrm {i} \cdot ({\frac {k}{N}})}\cdot c_{j}}$

Ојлеров идентитет гласи: ${\displaystyle e^{2\pi \mathrm {i} }=1}$. Такође важи ${\displaystyle {\overline {e^{\mathrm {i} \phi }}}=e^{-\mathrm {i} \phi }}$ и ${\displaystyle {\overline {z_{1}+z_{2}}}={\overline {z_{1}}}+{\overline {z_{2}}}}$.

Стога можемо још упростити израз:

${\displaystyle {\hat {c}}_{N-k}=\sum _{j=0}^{N-1}1\cdot e^{2\pi \mathrm {i} \cdot ({\frac {k}{N}})}\cdot c_{j}=\sum _{j=0}^{N-1}e^{2\pi \mathrm {i} \cdot {\frac {k}{N}}}\cdot c_{j}=\sum _{j=0}^{N-1}{\overline {e^{-2\pi \mathrm {i} \cdot {\frac {k}{N}}}}}\cdot c_{j}={\overline {{\hat {c}}_{k}}}}$

Што ће рећи, ${\displaystyle {\hat {c}}\in {\mathbb {C}}^{N}}$ није реалан, али само N независних вредности (уместо 2N).

За ИДФТ можемо закључити следеће: Уколико за ${\displaystyle {\hat {c}}\in {\mathbb {C}}^{N}}$ важи ${\displaystyle {\hat {c}}_{N-k}={\overline {{\hat {c}}_{k}}}}$ за све ${\displaystyle k=0,\dots ,N-1}$, онда је ИДФТ реалан вектор ${\displaystyle c\in \mathbb {R} ^{N}}$.

Ако је сигнал периодичан, онда није битно да ли трансформишемо у опсегу ${\displaystyle 0,\dots ,N-1}$ или ${\displaystyle k,\dots ,N-1+k}$. Индексна променљива j треба да обухвати N опсег, али није битно где он почиње односно где се завршава (ово важи само за случај да је сигнал периодичан, тј. да се вектор ${\displaystyle k,\dots ,N-1+k}$ периодично понавља). Присетимо се: за ${\displaystyle w}$ важи ${\displaystyle w^{N}=1}$. Онда ${\displaystyle w^{N+k}=w^{N}\cdot w^{k}=1\cdot w^{k}=w^{k}}$.

У пракси често желимо да разлика у индексима буде истовремено и разлика у времену или раздаљини два мерења

${\displaystyle t_{n}=nT,n=1-M,\dots ,N-M}$, ${\displaystyle T}$ је периода нашег мерења.

Често желимо и да коефицијентима доделимо фреквенцију тако да су центриране око ${\displaystyle 0}$

${\displaystyle \omega _{n}:=2\pi {\frac {n}{NT}},n=1-K,...,N-K}$, ${\displaystyle K}$ је негде у близини ${\displaystyle {\frac {N}{2}}}$.

Узмимо неку функцију ${\displaystyle f}$ којој додељујемо ${\displaystyle x\in {\mathbb {C}}^{N}}$ тако да ${\displaystyle x_{n}=f(t_{n})}$.

ДФТ је онда ${\displaystyle y_{n}={\hat {f}}(\omega _{n})=F(\omega _{n})}$.

Из тога следи:

${\displaystyle F(\omega _{n})=\sum _{j=1-M}^{N-M}e^{-2\pi \mathrm {i} {\frac {njT}{NT}}}x_{j}=\sum _{j=1-M}^{N-M}e^{-\mathrm {i} \,\omega _{n}\cdot t_{j}}f(t_{j})}$

а ИДФТ је

${\displaystyle f(t_{n})=x_{n}={\frac {1}{N}}\sum _{j=1-K}^{N-K}e^{-2\pi \mathrm {i} {\frac {nkT}{NT}}}y_{j}={\frac {1}{N}}\sum _{j=1-K}^{N-K}e^{\mathrm {i} \omega _{j}\cdot t_{n}}F(\omega _{j})}$

Ситуација: Звук који желимо да снимимо има следећи облик (када би га снимао аналоган микрофон):

Пошто је наш микрофон дигиталан, ми можемо само да снимимо појединачне вредности. На нашем компјутеру добијамо:

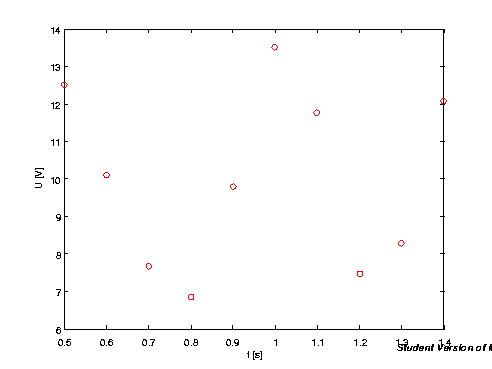
Наш циљ је да избацимо све фреквенције које су „тише“ (тј. које имају амплитуду) од 1 V. Прво правимо табелу:

<math>t_i =\,</math>0.5000    0.6000    0.7000    0.8000    0.9000    1.0000    1.1000    1.2000    1.3000    1.4000

<math>f(t_i) =\,</math>12.5000   10.0995   7.6644    6.8554    9.7905   13.5000   11.7546    7.4815    8.2905    12.0636

Имамо 10 вредности на 1 секунду, што ће рећи периода нашег мерења је ${\displaystyle T=0.1\,}$, а фреквенција ${\displaystyle freq={\frac {1}{T}}=10Hz}$. Стога ми можемо да реконструишемо талас до 5 Hz. Уколико у нашем оригиналном сигналу има фреквенција виших од 5 Hz онда ће наша реконструкција имати грешку. Али, као и увек у животу, човек мора бити оптимистичан те ћемо ми претпоставити да нема виших фреквенција (то је уосталом и један од разлога зашто компакт-диск има фреквенцију од око 41 kHz; људско ухо може да региструје тек до 20 kHz!).

Следи израчунавање ${\displaystyle \omega _{i}\,}$. Нас занимају само вредности везане за позитивне индексе:

${\displaystyle n=1-K,\ldots ,N-K;K=N/2=5;\,}$

${\displaystyle n=-4,\ldots ,5\,}$

${\displaystyle N\cdot T=10\cdot .1=1}$

${\displaystyle \omega _{0}=2\pi {\frac {0}{NT}}=0,\omega _{1}=2\pi ,\omega _{2}=4\pi ,\ldots ,\omega _{5}=10\pi }$

Сада имамо све вредности и можемо да почнемо са рачунањем:

${\displaystyle F(\omega _{0}=0)=\sum _{j=0}^{N-1=9}e^{-\mathrm {i} \cdot 0\cdot t_{j}}\cdot f(t_{j})=\sum _{j=0}^{9}f(t_{j})=100=y_{0}={\hat {c}}_{0}}$

${\displaystyle F(\omega _{1}=2\pi )=\sum _{j=0}^{N-1=9}e^{-\mathrm {i} \cdot 2\pi \cdot t_{j}}\cdot f(t_{j})=\ldots =0-3.5\mathrm {i} =y_{1}={\hat {c}}_{1}}$

${\displaystyle F(\omega _{2}=4\pi )=\sum _{j=0}^{N-1=9}e^{-\mathrm {i} \cdot 4\pi \cdot t_{j}}\cdot f(t_{j})=\ldots =15+0\mathrm {i} =y_{2}={\hat {c}}_{2}}$

Израчунавање осталих коефицијената иде аналогно, те ћемо их овде само навести као резултате:

${\displaystyle F(\omega _{3}=6\pi )=2.5-3\mathrm {i} =y_{3}={\hat {c}}_{3}}$

${\displaystyle F(\omega _{4}=8\pi )=6.7586e-14+2.8240e-14i=y_{4}={\hat {c}}_{4}}$

Имамо ${\displaystyle {\hat {c}}\,}$, сада желимо да избацимо све превише „тихе“ тонове. Требају нам ${\displaystyle c_{k}\,}$:

${\displaystyle c={\hat {c}}/N\Rightarrow c_{i}={\hat {c}}_{i}/10}$

${\displaystyle c_{i}:\,}$ 10 -0.35i 1.5 - 0i 0.25 - 0.3i 0 + 0i

Знамо да важи: ${\displaystyle c_{0}=a_{0},c_{i>0}={\frac {1}{2}}(a_{i}-b_{i}\mathrm {i} )}$. На тај начин можемо да израчунамо ${\displaystyle a_{i}\,}$ и ${\displaystyle b_{i}\,}$:

${\displaystyle a_{0}=10\,}$

${\displaystyle a_{1}-b_{1}\mathrm {i} =-0.7\mathrm {i} \Rightarrow a_{1}=0,b_{1}=0.7\,}$

Остале амплитуде:

${\displaystyle a_{2}=3\,}$

${\displaystyle a_{3}=0.5\,}$

${\displaystyle b_{3}=0.6\,}$

${\displaystyle a_{4}=b_{4}=0\,}$

Из ${\displaystyle a_{4}=b_{4}=0\,}$ можемо да закључимо да фреквенција од 4 Hz нема у нашем сигналу. Често је врло згодно навести све амплитуде у графикону. Амплитуда ${\displaystyle A_{k}\,}$ за неку фреквенцију ${\displaystyle k}$ је ${\displaystyle A_{k}={\sqrt {(a_{k}^{2}+b_{k}^{2})}}}$. У нашем случају наш фреквентни спектрум изгледа овако:

Све ${\displaystyle a_{i}\,}$ и ${\displaystyle b_{i}\,}$ за које важи ${\displaystyle {\sqrt {(a_{i}^{2}+b_{i}^{2})}}<1}$ избацујемо и на крају добијамо реконструисану и обрађену функцију:

${\displaystyle f(t)=10+3\cos(2\omega t)\,}$

Сада можемо да поново да израчунамо ${\displaystyle f(t_{i})\,}$ или да се послужимо ИДФТ и тако прерађен сигнал снимимо у меморију.

#include <stdio.h>
#include <math.h>
#include <complex.h>

#define pi 3.14159265
#define N 1000
#define T 0.001
#define FREQ 25

double my_function (double t )
{
	 /* violina svira ton od 25 Hz */
	 double ugaona_brzina = 2 * pi * FREQ;
	 return 5 + 10 * cos(ugaona_brzina * t) + 15 * cos(2 * (ugaona_brzina * t) ) 
			+ 20 * sin (3 * (ugaona_brzina * t) );

}

complex double get_fourier_coef (double omega_n, double* t, double* f  )
{
	 complex double coeff = 0;

	int k = 0;

	for (k = 0; k < N; k ++ )
	{
		// f[k] == f(t[k] );
		coeff += cexp (- I * omega_n * t[k]) * f[ k] ;
	}
	return coeff;
}

int main()
{
	double t[N];
	double omega[N];
	double f[N];

	double a[N/2+1];
	double phi[N/2+1];
	int n = 0;

	complex double coeff[N];
	
	/* pripremi vektore t i f_t -> nas signal je f_t !*/
	t[0] = 0;
	f[0] = my_function (t[0] );
	omega[0] = 0;

	for (n = 1; n < N; n ++ )
	{
		omega[n] = 2 * pi * n / (N * T );
		t[n] = n * T;
		f[n] = my_function (t[n] );	
	}

 
	/* izracunavanje koeficijenata */
	for (n = 0; n < N/2+1; n ++ )
	{
		coeff[n] = get_fourier_coef (omega[n], t, f );
		if (cabs(coeff[n]) > 0.1 ){
			printf ("# Koeficijent %d:  %e * e^i*%e\n", n, cabs(coeff[n]), carg(coeff[n]) ); 
		}
	}
	
	

	/* krece inverzija: */		
	a[0] = cabs(coeff[0]) / N;
	phi[0] = 0;
	for (n = 1; n < N/2+1; n++ )
	{
		if (cabs(coeff[n]) > 0.1 )
		{
			// c = 1/2 (a + ib ), zato a = 2 * |c|, b == 0 
			a[n] = 2  * cabs(coeff[n]) / N; 

			if (abs (carg(coeff[n])) > 0.001 )
			{
				phi[n] = carg(coeff[n] );
			}
			 else 
			{
				phi[n] = 0;
			}
		} 
		else 
		{
			a[n] = 0;
			phi[n] = 0;
		}
	}


	/* predstavljanje rezultata: */
	printf ("Nasa rekonstrukcija:\n f (t) = %e", a[0] );
	for (n = 1; n < N/2+1; n++ )
	{

		if (a[n] )
		{
			if (phi[n] )
			{
				printf (" + %e * cos (%d * (2 * pi * t + %e) )", a[n], n, phi[n] );
			}
			else
			{
				printf ("+ %e * cos (%d * 2 * pi * t )", a[n], n );
			}
		}
	}
	printf ("\n" );
	

	return 0;
}

• Дуалност по Понтрјагину