கோட்டுரு (கணிதம்)

கணிதத்தில் கோட்டுரு (Graph) என்பது, சில இணைகள் ஒன்றுடன் ஒன்று இணைக்கப்பட்ட ஒரு தொகுதி பொருட்களின் பண்புருப் பதிலீட்டைக் (abstract representation) குறிக்கும். இவ்வாறு கணிதப் பண்புருவாக்கத்தினால் ஒன்றுடன் ஒன்று இணைக்கப்பட்ட பொருட்கள் கணுக்கள் அல்லது முனைகள் எனப்படுகின்றன. இவற்றை இணைக்கும் இணைப்புகளை விளிம்புகள் என்கின்றனர். பொதுவாகக் கோட்டுருக்கள் வரைபட வடிவில் காட்டப்படுகின்றன. இவற்றில் புள்ளிகள் கணுக்களையும், அவற்றை இணைக்கும் நேர் கோடுகள் அல்லது வளை கோடுகள் விளிம்புகளையும் குறிக்கின்றன. கோட்டுரு பிரிநிலைக் கணிதத்தின் ஆய்வுப் பொருட்களுள் ஒன்றாக அமைகின்றது.

விளிம்புகள் திசையுள்ளனவாகவோ (சமச்சீரற்ற) அல்லது திசையற்றனவாகவோ (சமச்சீர்) இருக்கலாம். எடுத்துக்காட்டாக, புள்ளிகள் ஒரு நிகழ்வில் கலந்து கொள்ளும் ஆட்களைக் குறிப்பதாக வைத்துக்கொள்ளலாம். இங்கே இருவர் கைகுலுக்கிக் கொள்ளும்போது ஒரு விளிம்பு (இணைப்பு) உருவாகிறது. ஆள் A, B யுடன் கைகுலுக்கும் போது B யும் A யுடன் கை குலுக்குகிறார். இதனால் இக் கோட்டுரு திசையற்றது. இன்னொரு வகையில் பார்க்கும்போது, A க்கு B யைத் தெரியும் எனில் அங்கும் ஒரு விளிம்பு உருவாகிறது. ஆனாலும் B க்கு A யைத் தெரிய வேண்டியதில்லை ஆதலால் இங்கு உருவாகும் கோட்டுரு திசையுள்ளது ஆகும். இதன் விளிம்புகள் திசையுள்ள விளிம்புகள்.

உச்சியைக் "கணு", "புள்ளி" ஆகிய சொற்களாலும், விளிம்பைக் "கோடு" என்றும் குறிப்பதுண்டு. கோட்டுருவியலின் அடிப்படையான விடயம் கோட்டுரு ஆகும். கோட்டுருவுக்கான ஆங்கிலச் சொல் "graph" ஆனது இப்பொருளில் முதன்முதலாக 1878 இல் ஜேம்ஸ் சில்வெஸ்டரால் பயன்படுத்தப்பட்டது.^[1][2]

கோட்டுருக்கள் வேறுபட்ட பல வரையறைகள் கொண்டுள்ளன. இக்கட்டுரையில் கோட்டுருக்களை வரையறுக்கும் அடிப்படையான வழிகளும் தொடர்புள்ள கணித அமைப்புகளும் தரப்படுகிறது.

"கோட்டுரு" என்பது G = (V, E) என்ற வரிசைச் சோடி. இதில் V = முனைகள் என்றழைக்கப்படும் உறுப்புகளுடைய கணம்; E = விளிம்புகள் என்றழைக்கப்படும் இரு முனைகளை இணைக்கும் கோடுகளின் கணம். இணைப்புகள் அல்லது கோடுகள் எனவும் சில இடங்களில் விளிம்புகள் குறிப்பிடப்படுகின்றன.

திசையுள்ள கோட்டுருவிலிருந்து வேறுபடுத்திக் காட்டுவதற்காக இக்கோட்டுரு திசையற்ற கோட்டுரு எனவும் பல்கோட்டுருவிலிருந்து வேறுபடுத்திக் காட்டுவதற்காக எளிய கோட்டுரு எனவும் அழைக்கப்படுகிறது.^[3][4]

x, y முனைகள் இரண்டும் {x, y} விளிம்பின் இறுதிப்புள்ளிகள் எனப்படும். விளிம்பானது x, y முனைகளை இணைக்கிறது என்றும் முனைகளில் படுகிறது அல்லது படுகை விளிம்பு என்றும் அழைக்கப்படுகிறது. எந்த விளிம்பையும் சாராத முனைகளும் ஒரு கோட்டுருவில் இருக்கலாம்.

பல்கோட்டுரு என்பது ஒரே சோடி முனைகளுக்கு ஒன்றுக்கு மேற்பட்ட விளிம்புகள் கொண்ட கோட்டுருவாகும். சில நூல்கள் பல்கோட்டுருக்களைக் கோட்டுருக்கள் எனக் குறிப்பிடுவதும் உண்டு.^[5][6]

சிலசமயங்களில் கோட்டுருக்களில் கண்ணிகள் (ஒரு முனையை அதனுடனேயே இணைக்கும் விளிம்பு) அனுமதிக்கப்படுகின்றன. இத்தகையக் கோட்டுருக்களில் விளிம்புகளின் கணம் இரு-கணங்களாக இல்லாமல் பல்கணங்களாக வரையறுக்கப்படுகின்றன. இக்கோட்டுருக்கள் கண்ணிகள் கொண்ட கோட்டுருக்கள் என அழைக்கப்படுகின்றன. கண்ணிகளை அனுமதிக்கும் சூழலில், இவை சுருக்கமாகக் கோட்டுருக்கள் என்றும் அழைக்கப்படுகின்றன.

பொதுவாக முனைகளின் கணம் V முடிவுறு கணமாகக் கொள்ளப்படுகிறது; முனைகளின் கணம் V முடிவுறு கணமாக இருப்பதால், விளிம்புகளின் கணமும் முடிவுறு கணமாக அமைகிறது. "முடிவுறாக் கோட்டுரு"க்கள் கருத்தில் கொள்ளப்பட்டாலும் அவை ஈருறுப்பு உறவின் சிறப்பு வகையாகவேக் கருதப்படுகிறது. ஏனெனில் முடிவுறு கோட்டுருக்களுக்கான பெரும்பான்மையான முடிவுகளை முடிவுறாக் கோட்டுருக்களுக்கு நீட்டிக்க முடிவதல்லை என்பதோடு அவற்றுக்கு வேறுவிதமான நிறுவல்கள் தேவைப்படுகிறது.

முனைகளின் கணத்தை வெற்றுக் கணமாகக் கொண்ட கோட்டுரு வெற்று கோட்டுருவாகும். அதாவது வெற்றுக் கோட்டுரு என்பது முனைகளே இல்லாத கோட்டுருவாகும். ஒரு கோட்டுருவின் முனைகளின் எண்ணிக்கை அதாவது முனைகணத்தின் அளவு (${\displaystyle |V|}$), அக்கோட்டுருவின் வரிசை என்றும், விளிம்புகளின் எண்ணிக்கை அல்லது விளிம்பு கணத்தின் அளவு (${\displaystyle |E|}$) அக்கோட்டுருவின் அளவு என்றும் அழைக்கப்படும். ஒரு முனையின் படுகை விளிம்புகளின் எண்ணிக்கை அம்முனையின் படி அல்லது வலு எனப்படும். கண்ணிகள் இரு விளிம்புகளாக எண்ணப்படுகின்றன.

n வரிசை கொண்ட கோட்டுருவின் ஒவ்வொரு முனையின் பெருமப்படி n − 1 (கண்ணிகள் அனுமதிக்கப்டும்போது n + 1) ஆகவும், அதிகபட்ச விளிம்புகளின் எண்ணிக்கை n(n − 1)/2 (கண்ணிகள் அனுமதிக்கப்படும்போது n(n + 1)/2) ஆகவும் இருக்கும்.

கோட்டுருவின் முனைகள் மீது விளிம்புகள் அண்மை உறவு எனப்படும் சமச்சீர் உறவை வரையறுக்கின்றன. {x, y} ஒரு விளிம்பாக இருந்தால் x மற்றும் y இரண்டும் அண்மை முனைகள் அல்லது அடுத்துள்ள முனைகள் என அழைக்கப்படும்.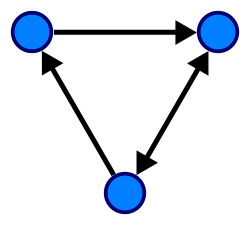

ஒரு கோட்டுருவின் ஒவ்வொரு விளிம்பும் திசையுடையதாக இருந்தால் அக்கோட்டுரு "திசை கோட்டுரு" எனப்படும்.

திசை கோட்டுரு என்பது G = (V, E) என்ற வரிசைச் சோடிகளைக் குறிக்கும்:

• ${\displaystyle V}$ - முனைகளின் கணம்;
• ${\displaystyle E\subseteq \{(x,y)\in V\times V:x\neq y\}\,}$ - வரிசைப்படுத்தப்பட்ட இரு வெவ்வேறான முனைகளை இணைக்கும் விளிம்புகளின் கணம்.

இவ்விளிம்புகள் திசை விளிம்புகள், திசை இணைப்புகள், அம்புகள் அல்லது விற்கள் எனவும் அழைக்கப்படுகின்றன.

இக்கோட்டுருக்கள் "திசையுள்ள எளிய கோட்டுருக்கள்" எனப்படுகின்றன.

(x, y) விளிம்பு x இலிருந்து y நோக்கி திசை கொண்டுள்ளது. x , y ஆகிய இருமுனைகளும் விளிம்பின் "இறுதிப்புள்ளிகள்" எனவும், x விளிம்பின் "வால்" மற்றும் y விளிம்பின் "தலை" எனவும் அழைக்கப்படுகின்றன. விளிம்பானது x , y முனைகளை இணைக்கிறது அல்லது அவற்றில் "படு"கிறது எனப்படுகிறது. (y, x) என்ற விளிம்பானது (x, y) விளிம்பின் நேர்மாறு விளிம்பாகும். எந்தவொரு விளிம்புடனும் இணைக்கப்படாத முனைகள் ஒரு கோட்டுருவில் இருக்கலாம். ஒரே தலை மற்றும் ஒரே வாலைக் கொண்ட விளிம்புகள் பல்விளிம்புகள் எனப்படும்.

திசையுள்ள பல்கோட்டுருக்கள்

பல்விளிம்புகளைக் கணக்கில் கொள்வதற்காகத் திசை கோட்டுருவானது ஒரு வரிசையுள்ள மும்மையாக G = (V, E, ϕ) வரையறுக்கப்படுகிறது:^[5][7]

• ${\displaystyle V}$ - முனைகளின் கணம்;
• ${\displaystyle E}$ - விளிம்புகளின் கணம்;
• ${\displaystyle \phi \colon E\rightarrow (x,y)\in V\times V:x\neq y\}\,}$ என்பது ஒவ்வொரு விளிம்பையும் ஒரு வரிசைச் சோடி முனைகளுடன் (வெவ்வேறான இரு முனைகள்) கோர்க்கும் "படுகைச் சார்பு" (incidence function) ஆகும்.

குழப்பம் தவிர்க்க முதல் வகையான கோட்டுருக்கள் "திசையுள்ள எளிய கோட்டுரு"க்கள் எனவும் பல்விளிம்புகளுடைய கோட்டுருக்கள் "திசையுள்ள பல்கோட்டுருக்கள்" எனவும் அழைக்கப்படுகிறன.

கண்ணி

ஒரு முனையை அதனுடனேயே இணைக்கும் விளிம்பானது கண்ணி என அழைக்கப்படும். மேலே தரப்பட்ட இரு வரையறைகளில் கண்ணிகள் இருக்க முடியாது. கண்ணிகள் அனுமதிக்கப்படுவதற்கு அவ்வரையறைகள் பின்னுள்ளவாறு நீட்டிக்கப்பட வேண்டும்.

• திசையுள்ள எளிய கோட்டுருக்களின் வரையறையிலுள்ள விளிம்புகளின் கணம் ${\displaystyle E\subseteq \{(x,y)\in V\times V:x\neq y\}\,}$ என்பது ${\displaystyle E\subseteq \{(x,y)\in V\times V\}\,}$ என நீட்டிக்கப்பட வேண்டும்.

இக்கோட்டுருக்கள் "கண்ணிகளை அனுமதிக்கும் திசையுள்ள எளிய கோட்டுருக்கள்" எனக் குறிப்பிடப்படுகின்றன.

• திசையுள்ள பல்கோட்டுருக்கள் வரையறையிலுள்ள படுகை சார்பு

${\displaystyle \phi \colon E\rightarrow (x,y)\in V\times V:x\neq y\}\,}$ என்பது ${\displaystyle \phi \colon E\rightarrow (x,y)\in V\times V\}\,}$ என நீட்டிக்கப்பட வேண்டும்.

இக்கோட்டுருக்கள் "கண்ணிகளை அனுமதிக்கும் திசையுள்ள பல்கோட்டுருக்கள்" எனக் குறிப்பிடப்படுகின்றன.

கண்ணிகளை அனுமதிக்கும் திசையுள்ள எளிய கோட்டுருவின் விளிம்புகள், அக்கோட்டுருவின் முனைகளின் மீது "அண்மை உறவை"த் தூண்டுகின்றன. ஒவ்வொரு {x, y} விளிம்பின் இறுதிப்புள்ளிகள் x , y இரண்டும் "அடுத்தமையும் முனைகள்" அல்லது "அண்மை முனைகள்" ஆகும்; இவ்வுறவானது குறியீட்டில் x ~ y என எழுதப்படுகிறது.

திசையற்ற மற்றும் திசையுள்ள விளிம்புகளைக் கொண்ட கோட்டுருவானது கலப்புக் கோட்டுரு என அழைக்கப்படும் எளிய கலப்புக் கோட்டுருவானது G = (V, E, A) என்ற மும்மையாகவும் கலப்பு பல்கோட்டுருவானது G = (V, E, A, ϕ_E, ϕ_A) ஆகவும் இருக்கும். இதில் V, E (திசையற்ற விளிம்புகள்), A (திசையுள்ள விளிம்புகள்), ϕ_E மற்றும் ϕ_A ஆகியவை திசையற்ற/திசையுள்ள கோட்டுருக்களுக்கு வரையறுக்கப்பட்டதைப் போல வரையறுக்கப்படுகின்றன.

A எடையிடப்பட்டக் கோட்டுரு (weighted graph) அல்லது வலையமைப்பு (network)^[8][9] என்பது ஒவ்வொரு விளிம்புக்கும் ஒரு எண் எடையாக இணைக்கப்பட்ட கோட்டுருவாகும்.^[10] கோட்டுருவுக்கான சூழலைப் பொறுத்து இந்த எடைகள் விலைகள், நீளங்கள், கொள்ளளவுகள் போன்றவைகளாக அமையலாம்.

ஒரு ஒழுங்கு கோட்டுருவின் அனைத்து முனைகளின் படியும் சமமாக இருக்கும். ஒரு திசை கோட்டுருவின் அனைத்து முனைகளின் உட்படிகளும் வெளிப்படிகளும் ஒன்றுக்கொன்று சமமாக இருந்தால் அது ஒழுங்கு திசை கோட்டுருவாகும்.^[11]

k படிகொண்ட முனைகளையுடைய ஒழுங்கு கோட்டுரு k‑ஒழுங்கு கோட்டுரு அல்லது k படியுடைய ஒழுங்கு கோட்டுரு எனப்படும்.

முழுக்கோட்டுருவின் ஒவ்வொரு வெவ்வேறான முனைகளின் இருமமும் தனித்ததொரு விளிம்பால் இணைக்கப்பட்டிருக்கும். "திசை முழுக்கோட்டுரு" என்பது ஒவ்வொரு வெவ்வேறான முனைகளின் இருமமும் விளிம்புகளின் தனித்ததொரு இருமத்தால் இணைக்கப்பட்ட ஒரு திசைக்கோட்டுரு ஆகும்.

முடிவுறு கோட்டுருவின் முனைகளின் கணமும் விளிம்புகளின் கணமும் முடிவுறு கணங்களாக இருக்கும். முனைகளின் கணமும் விளிம்புகளின் கணமும் முடிவுறா கணங்களாக இருந்தால் அக்கோட்டுருவானது முடிவுறாக் கோட்டுரு எனப்படும்.

குறைந்தபட்சம் ஒரு முனையும் ஒவ்வொரு முனைய சோடிகளுக்கிடையே ஒரு பாதையும் கொண்ட ஒரு திசையற்றக் கோட்டுரு இணைப்புள்ள கோட்டுரு என அழைக்கப்படுகிறது. ஒரேயொரு இணைப்புக் கூறுகொண்ட கோட்டுரு எனவும் இணைப்புள்ள கோட்டுருவைக் கூறலாம். இணைப்புள்ள கோட்டுருவில் சென்றடைய முடியாத முனைகளே இருக்காது. இணைப்புள்ள கோட்டுருக்கள் முழுக்கோட்டுருக்களாக இருக்க வேண்டிய அவசியமில்லை. (முழுக்கோட்டுருவில் ஒவ்வொரு முனைய சோடியும் ஒரு விளிம்பால் இணைக்கப்பட்டிருக்கும்.

ஒரு கோட்டுருவில் சென்றடைய முடியாத இரு முனைகள் இருந்தால் அக்கோட்டுரு, "இணைப்பற்றக் கோட்டுரு" அல்லது "இணைப்பிலாக் கோட்டுரு" எனப்படும். அதாவது எவையேனும் இரு முனைகளுக்கு இடையே பாதை அமையவில்லை எனில் அக்கோட்டுரு இணைப்பில்லாக் கோட்டுருவாகும்.

படத்திலுள்ள கோட்டுருவின் முனை "0" ஆனது கோட்டுருவின் வேறெந்த முனைகளுடனும் இணைக்கப்படவில்லை. இதனால் இக்கோட்டுரு இணைப்பற்றதாகிறது. கோட்டுருவிலிருந்து முனை "0" ஐ நீக்கினால் இதர பகுதி இணைப்புள்ள கோட்டுருவாக அமைவதையும் காணலாம்.

இருகூறு கோட்டுருவில், அதன் முனைகள் ${\displaystyle U,}$ ${\displaystyle V}$ என்ற இரு சேர்ப்பிலா மற்றும் சாரா கணங்களாகப் பிரிக்கப்பட்டிருக்கும். ${\displaystyle U}$ இலுள்ள ஒவ்வொரு முனையும் ${\displaystyle V}$ இலுள்ள ஒரு முனையோடு இணைக்கப்பட்டிருக்கும்.

முனை கணங்கள் ${\displaystyle U,}$ ${\displaystyle V}$ இரண்டும் இருகூறு கோட்டுருவின் "பாகங்கள்" எனப்படும். ஒற்றை-நீள சுழற்சிகளற்ற கோட்டுரு, இருகூறு கோட்டுருவாக இருக்கும்.^[12][13]

பாதை கோட்டுரு என்பது முனைகளை v₁, v₂, …, v_n என வரிசைப்படுத்தக் கூடிய கோட்டுருவாகும். {v_i, v_i+1} (i = 1, 2, …, n − 1) என்பது இக்கோட்டுருவின் விளிம்புகளாகும்.

1. குறைந்தபட்சம் இணைக்கப்பட இரு முனைகள்,
2. இரு இறுதிமுனைகள் (படி ஒன்றுள்ள முனைகள்),
3. படி இரண்டு கொண்ட பிற முனைகள் (இருந்தால்)

ஆகிய மூன்றையும் நிறைவு செய்யும் பாதையாகவும் பாதை கோட்டுருவைக் கருதலாம்.

ஒரேயொரு சுழற்சி கொண்ட கோட்டுரு சுழற்சி கோட்டுரு அல்லது வட்டக் கோட்டுரு ஆகும். சுழற்சி கோட்டுருவில் அதன் முனைகள் (குறைந்தபட்சம் 3) மூடிய இணைப்பு கொண்டிருக்கும். n முனைகள் கொண்ட சுழற்சி கோட்டுரு C_n எனக் குறிக்கப்படுகிறது. C_n இன் முனைகளின் எண்ணிக்கையும் விளிம்புகளின் எண்ணிக்கையும் சமமாக இருக்கும். ஒவ்வொரு முனைக்கும் இரு படுகை விளிம்புகள் இருக்கும். இதனால் சுழற்சி கோட்டுருவின் ஒவ்வொரு முனையின் படி 2 ஆக இருக்கும்.

ஒரு சுழற்சி கோட்டுருவின் விளிம்புகள் அனைத்தும் ஒரே திசையில் திசையிடப்பட்டிருக்குமானால் அது திசை சுழற்சி கோட்டுரு எனப்படும்.

எந்தவிரு முனைகளும் "ஒரேயொரு" பாதையால் மட்டுமே இணைக்கப்பட்ட திசையற்ற கோட்டுருவானது மரம் (tree) என அழைக்கப்படுகிறது. "இணைப்புள்ள சுழலாத் திசையற்ற கோட்டுரு" எனவும் மரம் வரையறுக்கப்படுகிறது^[14].

மரங்களின் பொதுவற்ற ஒன்றிப்பு "காடு" எனப்படுகிறது. மேலும் "அதிகபட்சம்" ஒரு பாதையால் இணைக்கப்பட்ட முனைகளைக் கொண்ட திசையற்ற கோட்டுரு அல்லது திசையற்ற சுழலாக் கோட்டுரு எனவும் காடு வரையறுக்கப்படுகிறது.^[15]

பன்மரம் (polytree)^[16] என்பது ஒரு திசையுள்ள சுழற்சியற்றக் கோட்டுருவாகும். பன்மரத்தில் அமைந்துள்ள அடிப்படை திசையற்ற கோட்டுரு ஒரு மரமாக இருக்கும். அதாவது, பன்மரத்தின் திசையுள்ள விளிம்புகளைத் திசையில்லா விளிம்புகளாக மாற்றினால் கிடைக்கும் கோட்டுரு, ஒரு இணைப்புள்ள சுழற்சியற்றக் கோட்டுருவாக (மரமாக) இருக்கும்.

காட்டினைத் தன் அடிப்படைக் கோட்டுருவாகக் கொண்ட திசையுள்ள சுழற்சியற்றக் கோட்டுருவானது "பல்காடு" என அழைக்கப்படும். பல்காட்டின் திசையுள்ள விளிம்புகளைத் திசையற்ற விளிம்புகளாக மாற்றினால் திசையற்ற சுழற்சியற்றக் கோட்டுருவான காடு கிடைக்கும்.

• ஒரு இறுதிப்புள்ளியைப் பொதுமுனையாகக் கொண்ட இரு விளிம்புகள் அண்மை விளிம்புகள் அல்லது அடுத்துள்ள விளிம்புகள் (adjacent edges) எனப்படும். திசை கோட்டுருவில் ஒரு விளிம்பின் தலையாக உள்ள முனையானது மற்றொரு விளிம்பிற்கு வாலாக இருக்குமானால் அவ்விரு விளிம்புகளும் அடுத்தடுத்த விளிம்புகளாகும்.

இதேபோல ஒரே விளிம்பின் இறுதிப்புள்ளிகளாக அமையும் முனைகள் அண்மை முனைகள் அல்லது அடுத்துள்ள முனைகள் என்றும் திசை கோட்டுருவில் விளிம்பின் தலையாகவும் வாலாகவும் உள்ள இரு முனைகளும் அடுத்தடுத்த முனைகள் எனவும் அழைக்கப்படுகின்றன. ஆகும்.

ஒரு முனையை இறுதிப்புள்ளியாகக் கொண்ட விளிம்பு அம்முனையின் படுகை விளிம்பு எனப்படுகிறது..

• ஒரேயொரு முனையுடன் விளிம்புகளே இல்லாத கோட்டுருவானது அற்பக் கோட்டுரு (trivial graph) என்றும் முனைகளை மட்டும் கொண்டு விளிம்புகளே இல்லாத கோட்டுருவானது விளிம்புகளற்ற கோட்டுரு என்றும் அழைக்கப்படும். சிலசமயங்களில் முனைகளை மட்டும் கொண்டு விளிம்புகளே இல்லாத கோட்டுருவானது வெற்று கோட்டுரு என்றும் அழைக்கப்படுகிறது. இந்த இரண்டாவது வரையறையை அனைத்து கணிதவியலாளர்களும் ஏற்பதில்லை.

ஒன்று அல்லது இரண்டு கோட்டுருக்களைக் கொண்டு புதிய கோட்டுரு ஒன்றை உருவாக்கக் கூடிய செயலிகள் உள்ளன. அவற்றுள் சில:

• ஓருறுப்புச் செயலிகள்:
  • விளிம்புக் குறுக்கம்
  • வரிக் கோட்டுரு
  • இரட்டைக் கோட்டுரு
  • நிரப்பு கோட்டுரு
  • கோட்டுரு உருமாற்றம்
• ஈருறுப்புச் செயலிகள்:
  • கோட்டுருக்களின் பொதுவற்ற ஒன்றிப்பு
  • கார்ட்டீசியன் பெருக்கற்பலன்