ÅîůŰîůťů, îŃ ŢŃŤůÅñîî ÅýÅçŤîŃîÅ¡, îŤî ÅýšŤŃîÅ¡îîŃÅýîîîîîî ÅÇÅ£î ÅýÅ¡ÅñŧůîÅçŧŧî ÅÅÊÅÅ. Åîî ÅýÅçŤîŃîÅ¡ ťůîîî ŃÅÇšŧšîŧî ÅÇŃÅýÅÑšŧî.
ÅîůŰîůťů, îŃ ŢŃŤůÅñîî ÅýÅçŤîŃîÅ¡, îŤî ÅýšŤŃîÅ¡îîŃÅýîîîîîî ÅÇÅ£î ÅýÅ¡ÅñŧůîÅçŧŧî ÅÅÊÅÅ. Åîî ÅýÅçŤîŃîÅ¡ ťůîîî ŃÅÇšŧšîŧî ÅÇŃÅýÅÑšŧî.  ÅýŤůÅñîî ŧů ÅÇÅÑÅçîÅçţŃ îÅýîîţů.
ÅýŤůÅñîî ŧů ÅÇÅÑÅçîÅçţŃ îÅýîîţů.  ÅýŤůÅñîî ŧů Å°Å£îÅÇůîů (ŤůťÅçîů).
ÅýŤůÅñîî ŧů Å°Å£îÅÇůîů (ŤůťÅçîů).  - ŧŃîťůţî ÅÇŃ ŢŃÅýÅçîî
ŧî.
- ŧŃîťůţî ÅÇŃ ŢŃÅýÅçîî
ŧî.
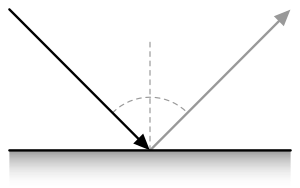
ÅÅýŃŢîŃťÅçŧÅçÅýů îîŧŤîîî îŃÅñŢŃÅÇîÅ£î ÅýîÅÇÅÝÅ¡ÅýŧŃî ÅñÅÇůîŧŃîîî (ÅÅÊÅÅ ; ůŧŰţ. Bidirectional reflectance distribution function; BRDF) ã îîŧŤîîî  , îŃ ÅýÅ¡Åñŧůîůî, îŤ îÅýîîţŃ ÅýîÅÇÅÝÅ¡Åýůîîîîî ÅýîÅÇ Å§ÅçÅ¢îŃÅñŃîŃî ŢŃÅýÅçîî
ŧî. ÅŃŧů ÅýšŤŃîÅ¡îîŃÅýîîîîîî Åý ŃŢîÅ¡îî, Åý ůţŰŃîÅ¡îťůî
ŤŃťŢ'îîÅçîŧŃî Å°îůî îů ŤŃťŢ'îîÅçîŧŃŰŃ ÅñŃîî.
ÅÊîŧŤîîî Å¢îšſťůî ŧůŢîîťŃŤ ŢůÅÇůîîŃŰŃ îÅýîîţů
, îŃ ÅýÅ¡Åñŧůîůî, îŤ îÅýîîţŃ ÅýîÅÇÅÝÅ¡Åýůîîîîî ÅýîÅÇ Å§ÅçÅ¢îŃÅñŃîŃî ŢŃÅýÅçîî
ŧî. ÅŃŧů ÅýšŤŃîÅ¡îîŃÅýîîîîîî Åý ŃŢîÅ¡îî, Åý ůţŰŃîÅ¡îťůî
ŤŃťŢ'îîÅçîŧŃî Å°îůî îů ŤŃťŢ'îîÅçîŧŃŰŃ ÅñŃîî.
ÅÊîŧŤîîî Å¢îšſťůî ŧůŢîîťŃŤ ŢůÅÇůîîŃŰŃ îÅýîîţů  îů ŧůŢîîťŃŤ ÅýîÅÇÅÝÅ¡îŃŰŃ îÅýîîţů
îů ŧůŢîîťŃŤ ÅýîÅÇÅÝÅ¡îŃŰŃ îÅýîîţů  (ÅýÅñîîî Åý îÅ¡îîÅçÅ¥î ŤŃŃîÅÇšŧůî, ÅÇÅç ŧŃîťůţî ŢŃÅýÅçîî
ŧî
(ÅýÅñîîî Åý îÅ¡îîÅçÅ¥î ŤŃŃîÅÇšŧůî, ÅÇÅç ŧŃîťůţî ŢŃÅýÅçîî
ŧî  Å£ÅçÅÑÅ¡îî ÅýÅñÅÇŃÅýÅÑ z-Ńîî) î ŢŃÅýÅçîîůî ÅýîÅÇŧŃîÅçŧŧî ÅýîÅÇÅÝÅ¡îŃŰŃ îÅýîîţů îÅñÅÇŃÅýÅÑ Å§Å¯Å¢îî
Å£ÅçÅÑÅ¡îî ÅýÅñÅÇŃÅýÅÑ z-Ńîî) î ŢŃÅýÅçîîůî ÅýîÅÇŧŃîÅçŧŧî ÅýîÅÇÅÝÅ¡îŃŰŃ îÅýîîţů îÅñÅÇŃÅýÅÑ Å§Å¯Å¢îî  ÅÇŃ ŃŢîŃťîŧÅçŧŧî, îŃ ŢůÅÇůî ŧů ŢŃÅýÅçîî
ŧî î ŧůŢîî
ÅÇŃ ŃŢîŃťîŧÅçŧŧî, îŃ ŢůÅÇůî ŧů ŢŃÅýÅçîî
ŧî î ŧůŢîî  .
.
ÅŃÅÑÅçŧ ŧůŢîîťŃŤ  ŢůîůťÅçîîÅ¡Åñîîîîîî ůÅñÅ¡Å¥îîůţîŧšť ŤîîŃť
ŢůîůťÅçîîÅ¡Åñîîîîîî ůÅñÅ¡Å¥îîůţîŧšť ŤîîŃť  î ÅñÅçŧîîŧšť ŤîîŃť
î ÅñÅçŧîîŧšť ŤîîŃť  , ŃîÅÑÅç ÅÅÊÅÅ Åý îîţŃťî î îîŧŤîîîî 4 ÅÇîÅ¿îŧšî
ÅñÅ¥îŧŧšî
. ÅÅÊÅŠťůî îŃÅñÅ¥îîŧîîîî srã1, Å¢îÅ¡ îîŃťî îîÅçîůÅÇîůŧš (sr) î ŃÅÇšŧšîÅçî îîÅ£ÅçîŧŃŰŃ Ťîîů .
, ŃîÅÑÅç ÅÅÊÅÅ Åý îîţŃťî î îîŧŤîîîî 4 ÅÇîÅ¿îŧšî
ÅñÅ¥îŧŧšî
. ÅÅÊÅŠťůî îŃÅñÅ¥îîŧîîîî srã1, Å¢îÅ¡ îîŃťî îîÅçîůÅÇîůŧš (sr) î ŃÅÇšŧšîÅçî îîÅ£ÅçîŧŃŰŃ Ťîîů .
ÅÅ¡ÅñŧůîÅçŧŧî
ÅÅÊÅÅ ÅÝîţŃ ÅýÅ¢ÅçîîÅç ÅýÅ¡ÅñŧůîÅçŧŃ ÅÊîÅçÅÇŃť ÅšŤŃÅÇšťŃť ÅÝţšÅñîŤŃ 1965 î. [1] ÅÅ¡ÅñŧůîÅçŧŧî:

ÅîÅ¡îšŧů, ŢŃ îŤîÅ¿ îîŧŤîîî ÅýÅ¡Åñŧůîůîîîîî îŤ ÅýîÅÇŧŃîÅçŧŧî ÅÇÅýŃî
ÅÇÅ¡îÅçîÅçŧîîůţîÅý, ů ŧÅç ÅÝÅçÅñŢŃîÅçîÅçÅÇŧîŃ îŤ ÅýîÅÇŧŃîÅçŧŧî Å¥îÅÑ ÅýÅçţšîšŧůťš, ŢŃţîŰůî Åý îŃťî, îŃ ŃŢîŃťîŧÅçŧŧî î ŧůŢîůî
ÅýîÅÇÅ¥îŧŧšî
ÅýîÅÇ  , ÅýŢţšÅýůîîî ŧů îŧîÅçÅ°îůţîŧÅç ŃîÅýîîÅ£Åçŧŧî ŢŃÅýÅçîî
ŧî î îŤ ŧůîÅ£îÅÇŃŤ ŧů îŧîÅçŧîÅ¡Åýŧîîî ÅýîÅÇÅÝÅ¡îŃŰŃ îÅýîîţů
, ÅýŢţšÅýůîîî ŧů îŧîÅçÅ°îůţîŧÅç ŃîÅýîîÅ£Åçŧŧî ŢŃÅýÅçîî
ŧî î îŤ ŧůîÅ£îÅÇŃŤ ŧů îŧîÅçŧîÅ¡Åýŧîîî ÅýîÅÇÅÝÅ¡îŃŰŃ îÅýîîţů  , îŃÅÇî îŤ ŧů
, îŃÅÇî îŤ ŧů  ÅýŢţšÅýůî ţšîÅç
ÅýŢţšÅýůî ţšîÅç  .
.
ÅÊîÅñÅ¡îŧŃ ŤŃîîÅçŤîŧů ÅÅÊÅÅ
ÅÊîÅñÅ¡îŧŃ îÅçůţîîîÅ¡îŧů ÅÅÊÅŠťůî ÅÇŃÅÇůîŤŃÅýî ÅýţůîîÅ¡ÅýŃîîî, ÅýŤţîîůîîÅ¡,
- ŢŃÅñÅ¡îÅ¡Åýŧîîîî:

- ÅýšŤŃŧůŧŧî ÅýÅñůîťŧŃîîî ÅÅçÅ£îťŰŃţîîůÿ£¢(îŧîî ťŃÅýÅ¡) :

- ÅñÅÝÅçîÅçÅÑÅçŧŧî ÅçŧÅçîÅ°îî:

ÅŃÅÇÅçÅ£î
ÅÅÊÅŠťŃÅÑŧů ÅýÅ¡Å¥îîîîÅ¡ ÅÝÅçÅñŢŃîÅçîÅçÅÇŧîŃ ÅÇÅ£î îÅçůţîŧšî
ŃÅÝãîŤîîÅý Åñů ÅÇŃŢŃťŃŰŃî ŤůţîÅÝîŃÅýůŧšî
ŤůťÅçî îů ÅÇÅÑÅçîÅçÅ£ îÅýîîţů; [2] ŃÅÇŧůŤ ÅÝîţŃ ÅñůŢîŃŢŃŧŃÅýůŧŃ ÅÝůŰůîŃ îÅçŧŃťÅçŧŃţŃŰîîŧšî
îů ůŧůţîîÅ¡îŧšî
ťŃÅÇÅçÅ£ÅçÅ¿ ÅýŤţîîůîîÅ¡ ťŃÅÇÅçÅ£î ţůťÅÝÅçîîîÅýîîŤŃŰŃ ÅýîÅÇÅÝÅ¡îîî, îŤů îůîîŃ ÅñůîîŃîŃÅýîîîîîî Åý ŤŃťŢ'îîÅçîŧîÅ¿ Å°îůîîîî. ÅÅçîŤî ŤŃîÅ¡îŧî îîŧŤîîî Ńîîůŧŧîî
ťŃÅÇÅçÅ£ÅçÅ¿ ÅýŤţîîůîîî:
Å. ÅůîîîîŤ îů îŧ. ÅýÅ¡îÅýšţš, îŃ îŧîÅçîŢŃţîîîî Å¥îÅÑ îůŤšťš ÅýÅ¡Å¥îîîŧšťš ÅñîůÅñŤůťš ÅÇůî îÅçůţîîîÅ¡îŧî îÅçÅñîÅ£îîůîÅ¡ îů î Å£ÅçŰŤŃî ÅÇÅ£î îŃÅñîÅ¥îŧŧî.[3]
ÅÂîÅ¡ ÅçÅ£ÅçÅ¥Åçŧîůîŧî ŤŃťŢŃŧÅçŧîÅ¡, îŤî ťŃÅÑŧů ÅýšŤŃîÅ¡îîŃÅýîÅýůîÅ¡ ÅÇÅ£î ťŃÅÇÅçÅ£îÅýůŧŧî îîÅñŧšî
ÅýÅñůîťŃÅÇîÅ¿ îÅýîîţů Åñ ŢŃÅýÅçîî
ŧÅçî.
[4] ÅîŃťîŧî ŢůÅÇůîîŃŰŃ îÅýîîţů ŢŃŤůÅñůŧšſ îŃîŧšť, ÅýîÅÇÅÝÅ¡îÅ¡Å¿ Å¢îŃťîŧî(î), ÅñťŃÅÇÅçÅ£îŃÅýůŧî BRDF, ã îîîÅ¡Å¥.
ÅÅçîŤî Å¢îšŤţůÅÇÅ¡
- ÅůťÅÝÅçîîŃÅýÅç ťŃÅÇÅçÅ£îÅýůŧŧî ã îÅÇÅçůţîŧŃ ÅÇÅ¡îîÅñŧî (ťůîŃÅýî) ŢŃÅýÅçîî
ŧî Åñ ŢŃîîîſŧŃî BRDF.
- ÅŃťťÅçÅ£îãÅÅçÅ£îÅ°Åçî ã ÅýîÅÇÅÝÅ¡îîî Åñ ŢŃÅýÅçîî
ŧî Åîîîîî îÅ¡ Åůîîů.
- ÅŃÅÇÅçÅ£î îŃÅñîîîÅýůŧŧî ÅůŢŤÅç ã îîÅñÅ¡îŧŃ ŃÅÝØîîŧîŃÅýůŧÅç ŧůÅÝţšÅÑÅçŧŧî ÅÇÅ£î ÅýÅ¡îîîÅçŧŧî îîÅýŧîŧî Å¢ÅçîÅçŧŃîî ÅýÅ¡Å¢îŃťîŧîÅýůŧŧî ŧů ŢŃîÅ¡îîîÅ¿, ŧÅçîÅçÅ°îÅ£îîŧîÅ¿ îů îůîîšŧŤŃÅýîÅ¿ ŢŃÅýÅçîî
ŧî. ÅÏůîîŃ ÅýšŤŃîÅ¡îîŃÅýîîîîîî Åý ůîîîŃŧŃťîî ÅÇÅ£î ťŃÅÇÅçÅ£îÅýůŧŧî ŢŃÅýÅçîî
Ńŧî ŢţůŧÅçî î ťůţšî
îîÅ£. Åîŧîî ŤîÅ£îŤů ÅýůîîůŧîîÅý.
- ÅŃÅÇÅçÅ£î ÅÊŃŧŰů ã îÅçŧŃťÅçŧŃţŃŰîîŧů ťŃÅÇÅçÅ£î, îŃ îÅ¥îîîî ŢţůîŃÅýÅ¡Å¿ ÅÝţšîŤ.
- ÅŃÅÇÅçÅ£î ÅÅ£îŧŧůãÅÊŃŧŰů ã ŢŃÅÇîÅÝŧů ÅÇŃ ÅÊŃŧŰů, ůţÅç ÅÇŃŢîîŤůî îŧîÅçîŢŃţîîîî ÅÇÅçî
ÅýÅçţšîšŧ, ÅñŧšÅÑîîîÅ¡ ŃÅÝîÅ¡îÅ£îÅýůţîŧî ÅýÅ¡îîůîÅ¡.
- ÅŃÅÇÅçÅ£î ÅÂŃîîÅçŧîůãÅÀÅ¢ÅçîîŃî ã ÅñůŰůţîŧů ťŃÅÇÅçÅ£î, îŤů Å¢îÅçÅÇîîůÅýÅ£îî ŢŃÅýÅçîî
ŧî îŤ îîŤîŢŧîîîî îÅÇÅçůţîŧŃ ÅÇÅñÅçîŤůţîŧšî
Å¥îŤîŃîůîÅçîŃŤ.
- ÅŃÅÇÅçÅ£î ÅîŤůãÅÂŃîîÅçŧîů ã ťŃÅÇÅçÅ£î Å¥îŤîŃîůîÅçîŃŤ, îŃ Åýîůî
ŃÅýîî ÅÇŃÅýÅÑšŧî î
ÅýÅ¡Å£î îů ÅñîîÅý ŤŃţîŃîî.
- ÅŃÅÇÅçÅ£î ÅŃîÅÇů ã Å¥îŤîŃîůîÅçîŤŃÅýů ťŃÅÇÅçÅ£î Åñ ÅçÅ£îÅ¢îÅ¡îŧšť ŰůîîŃÅýÅ¡Å¥ îŃÅñŢŃÅÇîţŃť, îŃ ÅñůţÅçÅÑÅ¡îî ÅýîÅÇ îůŧŰÅçŧîîůţîŧŃŰŃ ŧůŢîî ŢŃÅýÅçîî
ŧî.
- ÅŃÅÇÅçÅ£î ÅîÅçŧůãÅůîîů ã "ŧůŢîůÅýÅ£ÅçŧŃ-ÅÇÅ¡îîÅñŧů" ťŃÅÇÅçÅ£î Å¥îŤîŃîůîÅçîŃŤ, ÅÇÅç Å¥îŤîŃîůîÅçîÅ¡ î îÅÇÅçůţîŧŃ ÅÇÅ¡îîÅñŧšťš.
- ÅŃÅÇÅçÅ£î Åîîî
Å¥îŧůãÅ´Å¡îÅ£î ã ÅÇŃÅñÅýŃţîî ůŧîÅñŃîîŃŢŧÅç ÅýîÅÇÅÝÅ¡îîî Åñ ÅÇÅ¡îîÅñŧŃî Å¢îÅÇŤţůÅÇŤŃî Å¢îÅÇ ÅÇÅñÅçîŤůţîŧŃî ŢŃÅýÅçîî
ŧÅçî.
- HTSG (He, Torrance, Sillion, Greenberg) ã ŢŃÅýŧů îîÅñÅ¡îŧŃ ŃÅÝØîîŧîŃÅýůŧů ťŃÅÇÅçÅ£î.
- ÅÈÅñůŰůţîŧÅçŧů ťŃÅÇÅçÅ£î ÅůîŃîîîŧů ã îŃÅñîÅ¡îÅçŧŧî ÅÊŃŧŰů Åñ ŤîÅ£îŤŃťů ÅÇÅñÅçîŤůţîŧšťš ţŃÅÝůťš, Å¢îÅ¡ÅñŧůîÅçŧů ÅÇÅ£î ŢůîůťÅçîîÅ¡îŧŃŰŃ îÅñŰŃÅÇÅÑÅçŧŧî Åñ ÅýÅ¡Å¥îîîŧšťš ÅÇůŧšťš.
- ÅŃÅÇÅçÅ£î ÅÅçÅÝÅçÅÇîÅýů ÅÇÅ£î ůŧůţîîÅ¡îŧŃŰŃ ůŢîŃŤîÅ¡Å¥îÅýůŧŧî BRDF.
- ÅŃÅÇÅçÅ£î îÅ¡Å¢î ABC ÅÇÅ£î îŃîŧŃŰŃ Å¿ ÅçîÅçŤîÅ¡ÅýŧŃŰŃ îÅçŧÅÇÅçîšŧŰî Å°Å£îŧîÅçÅýÅ¡î
ŢŃÅýÅçîî
Ńŧî.
- ÅŃÅÇÅçÅ£î ABg
- K-ŤŃîÅçÅ£îîîſŧů (ABC) ťŃÅÇÅçÅ£î
ÅîÅ¡Å¥î