 –õ–µ–º–Ω—ñ—Å–∫–∞—Ç–∞ —ñ —ó—ó —Ñ–æ–∫—É—Å–∏
–õ–µ–º–Ω—ñ—Å–∫–∞—Ç–∞ —ñ —ó—ó —Ñ–æ–∫—É—Å–∏
Лемніската Бернуллі (грец. λημνίσκοζ — пов'язка) — плоска алгебрична крива, яку можна означити як геометричне місце точок  , для кожної з яких добуток відстаней до двох заданих точок
, –¥–ª—è –∫–æ–∂–Ω–æ—ó –∑ —è–∫–∏—Ö –¥–æ–±—É—Ç–æ–∫ –≤—ñ–¥—Å—Ç–∞–Ω–µ–π –¥–æ –¥–≤–æ—Ö –∑–∞–¥–∞–Ω–∏—Ö —Ç–æ—á–æ–∫  —Ç–∞
—Ç–∞  (—Ñ–æ–∫—É—Å—ñ–≤) –Ω–µ–∑–º—ñ–Ω–Ω–∞ —ñ –¥–æ—Ä—ñ–≤–Ω—é—î –∫–≤–∞–¥—Ä–∞—Ç—É –ø–æ–ª–æ–≤–∏–Ω–∏ –≤—ñ–¥—Å—Ç–∞–Ω—ñ –º—ñ–∂ —Ñ–æ–∫—É—Å–∞–º–∏.
(—Ñ–æ–∫—É—Å—ñ–≤) –Ω–µ–∑–º—ñ–Ω–Ω–∞ —ñ –¥–æ—Ä—ñ–≤–Ω—é—î –∫–≤–∞–¥—Ä–∞—Ç—É –ø–æ–ª–æ–≤–∏–Ω–∏ –≤—ñ–¥—Å—Ç–∞–Ω—ñ –º—ñ–∂ —Ñ–æ–∫—É—Å–∞–º–∏.
–¢–æ–±—Ç–æ, –¥–ª—è –∫–æ–∂–Ω–æ—ó —Ç–æ—á–∫–∏  –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏ –≤–∏–∫–æ–Ω—É—î—Ç—å—Å—è —Ä—ñ–≤–Ω—ñ—Å—Ç—å:
–ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏ –≤–∏–∫–æ–Ω—É—î—Ç—å—Å—è —Ä—ñ–≤–Ω—ñ—Å—Ç—å:
 .
.
де  — відстань між фокусами
— відстань між фокусами  .
.
–ù–∞–∑–≤–∞ –ø–æ—Ö–æ–¥–∏—Ç—å –∑ –∞–Ω—Ç–∏—á–Ω–æ–≥–æ –Ý–∏–º—É, –¥–µ ¬´–ª–µ–º–Ω—ñ—Å–∫–∞—Ç–æ—鬪 –Ω–∞–∑–∏–≤–∞–ª–∏ –±–∞–Ω—Ç–∏–∫, –∑ –¥–æ–ø–æ–º–æ–≥–æ—é —è–∫–æ–≥–æ –ø—Ä–∏–∫—Ä—ñ–ø–ª—è–ª–∏ –≤—ñ–Ω–æ–∫ –¥–æ –≥–æ–ª–æ–≤–∏ –ø–µ—Ä–µ–º–æ–∂—Ü—è –Ω–∞ —Å–ø–æ—Ä—Ç–∏–≤–Ω–∏—Ö —ñ–≥—Ä–∞—Ö. –¶—é –ª–µ–º–Ω—ñ—Å–∫–∞—Ç—É –Ω–∞–∑–∏–≤–∞—é—Ç—å –≤ —á–µ—Å—Ç—å —à–≤–µ–π—Ü–∞—Ä—Å—å–∫–æ–≥–æ –º–∞—Ç–µ–º–∞—Ç–∏–∫–∞ –Ø–∫–æ–±–∞ –ë–µ—Ä–Ω—É–ª–ª—ñ, —è–∫–∏–π –ø–æ–∫–ª–∞–≤ –ø–æ—á–∞—Ç–æ–∫ —ó—ó –≤–∏–≤—á–µ–Ω–Ω—é –≤ 1694 —Ä–æ—Ü—ñ.
Лемніската Бернуллі — алгебрична крива 4 порядку. Є окремим випадком овалів Кассіні та синусоїдальних спіралей.
–Ý—ñ–≤–Ω—è–Ω–Ω—è
–ù–µ—Ö–∞–π —Ñ–æ–∫—É—Å–∏ –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏ –ë–µ—Ä–Ω—É–ª–ª—ñ –∑–Ω–∞—Ö–æ–¥—è—Ç—å—Å—è –Ω–∞ –æ—Å—ñ  –≤ —Ç–æ—á–∫–∞—Ö
–≤ —Ç–æ—á–∫–∞—Ö  —ñ
—ñ  . –í—ñ–¥—Å—Ç–∞–Ω—å –º—ñ–∂ —Ñ–æ–∫—É—Å–∞–º–∏ –¥–æ—Ä—ñ–≤–Ω—é—î
. –í—ñ–¥—Å—Ç–∞–Ω—å –º—ñ–∂ —Ñ–æ–∫—É—Å–∞–º–∏ –¥–æ—Ä—ñ–≤–Ω—é—î  , –∞ —Ç–æ—á–∫–∞
, а точка  — початок координат ділить відрізок між фокусами навпіл.
–¢–æ–¥—ñ –Ω–∞—Å—Ç—É–ø–Ω—ñ —Ä—ñ–≤–Ω—è–Ω–Ω—è –∑–∞–¥–∞—é—Ç—å –ª–µ–º–Ω—ñ—Å–∫–∞—Ç—É –ë–µ—Ä–Ω—É–ª–ª—ñ:
— початок координат ділить відрізок між фокусами навпіл.
–¢–æ–¥—ñ –Ω–∞—Å—Ç—É–ø–Ω—ñ —Ä—ñ–≤–Ω—è–Ω–Ω—è –∑–∞–¥–∞—é—Ç—å –ª–µ–º–Ω—ñ—Å–∫–∞—Ç—É –ë–µ—Ä–Ω—É–ª–ª—ñ:

–ó—Ä–æ–±–∏–≤—à–∏ –Ω–µ—Å–∫–ª–∞–¥–Ω—ñ –ø–µ—Ä–µ—Ç–≤–æ—Ä–µ–Ω–Ω—è, –º–æ–∂–Ω–∞ –æ—Ç—Ä–∏–º–∞—Ç–∏ —Ä—ñ–≤–Ω—è–Ω–Ω—è —É —è–≤–Ω–æ–º—É –≤–∏–≥–ª—è–¥—ñ:

–í–∏–≤—ñ–¥

–ü—ñ–¥–Ω–µ—Å–µ–º–æ –≤ –∫–≤–∞–¥—Ä–∞—Ç —ñ —Ä–æ–∑–∫—Ä–∏—î–º–æ –¥—É–∂–∫–∏:

–ü—Ä–∏–≤–µ–¥–µ–º–æ –¥–æ –≤–∏–≥–ª—è–¥—É

–¶–µ –∫–≤–∞–¥—Ä–∞—Ç–Ω–µ —Ä—ñ–≤–Ω—è–Ω–Ω—è –≤—ñ–¥–Ω–æ—Å–Ω–æ  . –Ý–æ–∑–≤'—è–∑–∞–≤—à–∏ –π–æ–≥–æ, –æ—Ç—Ä–∏–º–∞—î–º–æ
. –Ý–æ–∑–≤'—è–∑–∞–≤—à–∏ –π–æ–≥–æ, –æ—Ç—Ä–∏–º–∞—î–º–æ

–î–æ–±—É–≤—à–∏ –∫–æ—Ä—ñ–Ω—å —ñ –≤—ñ–¥–∫–∏–Ω—É–≤—à–∏ –≤–∞—Ä—ñ–∞–Ω—Ç –∑ –≤—ñ–¥'—î–º–Ω–æ—é –¥—Ä—É–≥–æ—é –∑–º—ñ–Ω–Ω–æ—é, –æ—Ç—Ä–∏–º–∞—î–º–æ:

де додатній варіант визначає верхню половину лемніскати, від'ємний — нижню.

–ö—Ä–∏–≤–∞ –≤–∏–∑–Ω–∞—á–µ–Ω–∞ –ø—Ä–∏ ![{\displaystyle \varphi \in \left[0,{\frac {\pi }{4}}\right]\cup \left[{\frac {3\pi }{4}},{\frac {5\pi }{4}}\right]\cup \left[{\frac {7\pi }{4}},2\pi \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11be43317f89581ff6fe634be3e11b48e7ffc444) ;
;
–∞–±–æ –∂ –ø—Ä–∏ ![{\displaystyle \varphi \in \left[-{\frac {\pi }{4}},{\frac {\pi }{4}}\right]\cup \left[{\frac {3\pi }{4}},{\frac {5\pi }{4}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b3f461a5b8bb336e9bbf64e2c0412f86fcc917b)
 , –¥–µ
, –¥–µ 
–©–æ–± –∑–∞–¥–∞—Ç–∏ –ª–µ–º–Ω—ñ—Å–∫–∞—Ç—É –ø–æ –¥–≤–æ—Ö –¥–æ–≤—ñ–ª—å–Ω–∏—Ö —Ç–æ—á–∫–∞—Ö, –º–æ–∂–Ω–∞ –Ω–µ –≤–∏–≤–æ–¥–∏—Ç–∏ —Ä—ñ–≤–Ω—è–Ω–Ω—è –∑–∞–Ω–æ–≤–æ, –∞ –≤–∏–∑–Ω–∞—á–∏—Ç–∏ –ø–µ—Ä–µ—Ç–≤–æ—Ä–µ–Ω–Ω—è –∫–æ–æ—Ä–¥–∏–Ω–∞—Ç, –ø—Ä–∏ —è–∫–æ–º—É —Å—Ç–∞—Ä–∏–π (–¥–∞–Ω–∏–π) —Ñ–æ–∫—É—Å–Ω–∏–π –≤—ñ–¥—Ä—ñ–∑–æ–∫ –ø–µ—Ä–µ—Ö–æ–¥–∏—Ç—å –≤ –Ω–æ–≤–∏–π, —ñ –ø–æ–¥—ñ—è—Ç–∏ –Ω–∞ –ø—Ä–µ–¥—Å—Ç–∞–≤–ª–µ–Ω—ñ —Ä—ñ–≤–Ω—è–Ω–Ω—è —Ü–∏–º –ø–µ—Ä–µ—Ç–≤–æ—Ä–µ–Ω–Ω—è–º.
–ü—Ä–∏–∫–ª–∞–¥

Нехай, наприклад,  — фокуси.
— фокуси.
Існує прямокутна система координат (на рисунку —  ), в якій рівняння лемніскати має вигляд
), –≤ —è–∫—ñ–π —Ä—ñ–≤–Ω—è–Ω–Ω—è –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏ –º–∞—î –≤–∏–≥–ª—è–¥

–ù–µ–æ–±—Ö—ñ–¥–Ω–æ –≤–∏–∑–Ω–∞—á–∏—Ç–∏ –ø–µ—Ä–µ—Ç–≤–æ—Ä–µ–Ω–Ω—è —Å–∏—Å—Ç–µ–º–∏ –∫–æ–æ—Ä–¥–∏–Ω–∞—Ç, —â–æ –ø–µ—Ä–µ–≤–æ–¥–∏—Ç—å  –≤
–≤  . –¶–µ –ø–µ—Ä–µ—Ç–≤–æ—Ä–µ–Ω–Ω—è –∑–¥—ñ–π—Å–Ω—é—î—Ç—å—Å—è –≤ –¥–≤–∞ –µ—Ç–∞–ø–∏: –ø–∞—Ä–∞–ª–µ–ª—å–Ω–µ –ø–µ—Ä–µ–Ω–µ—Å–µ–Ω–Ω—è —ñ –ø–æ–≤–æ—Ä–æ—Ç.
. –¶–µ –ø–µ—Ä–µ—Ç–≤–æ—Ä–µ–Ω–Ω—è –∑–¥—ñ–π—Å–Ω—é—î—Ç—å—Å—è –≤ –¥–≤–∞ –µ—Ç–∞–ø–∏: –ø–∞—Ä–∞–ª–µ–ª—å–Ω–µ –ø–µ—Ä–µ–Ω–µ—Å–µ–Ω–Ω—è —ñ –ø–æ–≤–æ—Ä–æ—Ç.
Середина відрізка  —
—  , значить паралельний перенос тільки на
, –∑–Ω–∞—á–∏—Ç—å –ø–∞—Ä–∞–ª–µ–ª—å–Ω–∏–π –ø–µ—Ä–µ–Ω–æ—Å —Ç—ñ–ª—å–∫–∏ –Ω–∞  –ø–æ –æ—Å—ñ
–ø–æ –æ—Å—ñ  :
:

–ü—ñ—Å–ª—è –ø–µ—Ä–µ–Ω–æ—Å—É —Å–∏—Å—Ç–µ–º–∏ –∫–æ–æ—Ä–¥–∏–Ω–∞—Ç —ó—ó –ø–æ—Ç—Ä—ñ–±–Ω–æ –ø–æ–≤–µ—Ä–Ω—É—Ç–∏ –Ω–∞ –¥–µ—è–∫–∏–π –∫—É—Ç. –î–ª—è –≤–∏–∑–Ω–∞—á–µ–Ω–Ω—è –∫—É—Ç–∞ —Å–ø–æ—á–∞—Ç–∫—É –∑–Ω–∞–π–¥–µ–º–æ –≤—ñ–¥—Å—Ç–∞–Ω—å –º—ñ–∂ —Ñ–æ–∫—É—Å–∞–º–∏:

–∑–Ω–∞—á–∏—Ç—å  .
.
–¢–µ–ø–µ—Ä —ñ–∑ –≥–µ–æ–º–µ—Ç—Ä–∏—á–Ω–∏—Ö –º—ñ—Ä–∫—É–≤–∞–Ω—å –∑–Ω–∞–π–¥–µ–º–æ —Å–∏–Ω—É—Å —ñ –∫–æ—Å–∏–Ω—É—Å –∫—É—Ç–∞ –Ω–∞—Ö–∏–ª—É  –¥–æ –æ—Å—ñ
–¥–æ –æ—Å—ñ  :
:


–§–æ—Ä–º—É–ª–∏ –ø–µ—Ä–µ—Ç–≤–æ—Ä–µ–Ω–Ω—è:

–ü–æ—î–¥–Ω–∞–≤—à–∏ –æ–±–∏–¥–≤–∞ –ø–µ—Ä–µ—Ç–≤–æ—Ä–µ–Ω–Ω—è, –æ—Ç—Ä–∏–º–∞—î–º–æ —Å–∫—ñ–Ω—á–µ–Ω–Ω—ñ —Ñ–æ—Ä–º—É–ª–∏ –ø–µ—Ä–µ—Ö–æ–¥—É:

–î–ª—è —Ç–æ–≥–æ, —â–æ–± –æ—Ç—Ä–∏–º–∞—Ç–∏ —Ä—ñ–≤–Ω—è–Ω–Ω—è –≤ —Å—Ç–∞–Ω–¥–∞—Ä—Ç–Ω—ñ–π —Å–∏—Å—Ç–µ–º—ñ –∫–æ–æ—Ä–¥–∏–Ω–∞—Ç, –ø—ñ–¥—Å—Ç–∞–≤–∏–º–æ —Ü—ñ —Å–ø—ñ–≤–≤—ñ–¥–Ω–æ—à–µ–Ω–Ω—è –≤ –≤–∏—Ö—ñ–¥–Ω–µ —Ä—ñ–≤–Ω—è–Ω–Ω—è –∫—Ä–∏–≤–æ—ó:

–ü—ñ—Å–ª—è –ø–µ—Ä–µ—Ç–≤–æ—Ä–µ–Ω—å:

–¶–µ —Ä—ñ–≤–Ω—è–Ω–Ω—è –∑–∞–¥–∞—î –ª–µ–º–Ω—ñ—Å–∫–∞—Ç—É –∑ —Ñ–æ–∫—É—Å–∞–º–∏

–≤ —Å—Ç–∞–Ω–¥–∞—Ä—Ç–Ω—ñ–π –ø—Ä—è–º–æ–∫—É—Ç–Ω—ñ–π —Å–∏—Å—Ç–µ–º—ñ –∫–æ–æ—Ä–¥–∏–Ω–∞—Ç.

–¥–µ
 — радіус кривини лемніскати Бернуллі в певній точці;
— радіус кривини лемніскати Бернуллі в певній точці;
 — довжина дуги лемніскати від її початку до цієї точки.
— довжина дуги лемніскати від її початку до цієї точки.
–í–ª–∞—Å—Ç–∏–≤–æ—Å—Ç—ñ —Ç–∞ –æ—Å–æ–±–ª–∏–≤–æ—Å—Ç—ñ —Ñ–æ—Ä–º–∏
 –õ–µ–º–Ω—ñ—Å–∫–∞—Ç–∞, –≤–ø–∏—Å–∞–Ω–∞ –≤ –∫–æ–ª–æ
–õ–µ–º–Ω—ñ—Å–∫–∞—Ç–∞, –≤–ø–∏—Å–∞–Ω–∞ –≤ –∫–æ–ª–æ
- –î–ª—è –¥–æ–≤—ñ–ª—å–Ω–æ—ó —Ç–æ—á–∫–∏
 –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏ –ë–µ—Ä–Ω—É–ª–ª—ñ –∑ —Ñ–æ–∫—É—Å–∞–º–∏
–ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏ –ë–µ—Ä–Ω—É–ª–ª—ñ –∑ —Ñ–æ–∫—É—Å–∞–º–∏  —Ç–∞
—Ç–∞  —Å–ø—Ä–∞–≤–µ–¥–ª–∏–≤–µ –Ω–∞—Å—Ç—É–ø–Ω–µ —Ç–≤–µ—Ä–¥–∂–µ–Ω–Ω—è (–∞–ª—å—Ç–µ—Ä–Ω–∞—Ç–∏–≤–Ω–µ –æ–∑–Ω–∞—á–µ–Ω–Ω—è –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏):
—Å–ø—Ä–∞–≤–µ–¥–ª–∏–≤–µ –Ω–∞—Å—Ç—É–ø–Ω–µ —Ç–≤–µ—Ä–¥–∂–µ–Ω–Ω—è (–∞–ª—å—Ç–µ—Ä–Ω–∞—Ç–∏–≤–Ω–µ –æ–∑–Ω–∞—á–µ–Ω–Ω—è –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏):

де  — середина відрізка
— середина відрізка  .
.
–î–æ–≤–µ–¥–µ–Ω–Ω—è

–û—Ç–∂–µ :

- Лемніската — алгебрична крива четвертого порядку.
- –í–æ–Ω–∞ –º–∞—î –¥–≤—ñ –æ—Å—ñ —Å–∏–º–µ—Ç—Ä—ñ—ó: –ø—Ä—è–º–∞, –Ω–∞ —è–∫—ñ–π –ª–µ–∂–∏—Ç—å
 , і серединний перпендикуляр цього відрізка; для розглянутого випадку — вісь
, і серединний перпендикуляр цього відрізка; для розглянутого випадку — вісь  .
.
- –¢–æ—á–∫–∞, –¥–µ –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∞ –ø–µ—Ä–µ—Ç–∏–Ω–∞—î —Å–∞–º—É —Å–µ–±–µ, –Ω–∞–∑–∏–≤–∞—î—Ç—å—Å—è –≤—É–∑–ª–æ–≤–æ—é —á–∏ –ø–æ–¥–≤—ñ–π–Ω–æ—é —Ç–æ—á–∫–æ—é.
–î–ª—è —Ä–æ–∑–≥–ª—è–Ω—É—Ç–æ–≥–æ –≤–∏–ø–∞–¥–∫—É –ø–æ–¥–≤—ñ–π–Ω–æ—é —Ç–æ—á–∫–æ—é –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏ —î –ø–æ—á–∞—Ç–æ–∫ –∫–æ–æ—Ä–¥–∏–Ω–∞—Ç.
- Дотичні в подвійній точці лемніскати — прямі
 , —Å–∫–ª–∞–¥–∞—é—Ç—å –∑ –≤—ñ–¥—Ä—ñ–∑–∫–æ–º
, —Å–∫–ª–∞–¥–∞—é—Ç—å –∑ –≤—ñ–¥—Ä—ñ–∑–∫–æ–º  –∫—É—Ç–∏
–∫—É—Ç–∏  —ñ —î –≤–∑–∞—î–º–Ω–æ –ø–µ—Ä–ø–µ–Ω–¥–∏–∫—É–ª—è—Ä–Ω–∏–º–∏. : —Å—Ç–æ—Ä.155
—ñ —î –≤–∑–∞—î–º–Ω–æ –ø–µ—Ä–ø–µ–Ω–¥–∏–∫—É–ª—è—Ä–Ω–∏–º–∏. : —Å—Ç–æ—Ä.155
- –ö—É—Ç
 –º—ñ–∂ –¥–æ—Ç–∏—á–Ω–æ—é –¥–æ –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏ –≤ —ó—ó –¥–æ–≤—ñ–ª—å–Ω—ñ–π —Ç–æ—á—Ü—ñ —Ä–∞–¥—ñ—É—Å-–≤–µ–∫—Ç–æ—Ä–æ–º —Ç–æ—á–∫–∏ –¥–æ—Ç–∏–∫—É –¥–æ—Ä—ñ–≤–Ω—é—î: : —Å—Ç–æ—Ä.156
–º—ñ–∂ –¥–æ—Ç–∏—á–Ω–æ—é –¥–æ –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏ –≤ —ó—ó –¥–æ–≤—ñ–ª—å–Ω—ñ–π —Ç–æ—á—Ü—ñ —Ä–∞–¥—ñ—É—Å-–≤–µ–∫—Ç–æ—Ä–æ–º —Ç–æ—á–∫–∏ –¥–æ—Ç–∏–∫—É –¥–æ—Ä—ñ–≤–Ω—é—î: : —Å—Ç–æ—Ä.156
 .
.
- –î–æ—Ç–∏—á–Ω—ñ –¥–æ –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏, —è–∫—ñ –ø—Ä–æ–≤–µ–¥–µ–Ω—ñ –Ω–∞ –∫—ñ–Ω—Ü—è—Ö —Ö–æ—Ä–¥–∏, —â–æ –ø—Ä–æ—Ö–æ–¥–∏—Ç—å —á–µ—Ä–µ–∑ —ó—ó –ø–æ–¥–≤—ñ–π–Ω—É —Ç–æ—á–∫—É, –ø–∞—Ä–∞–ª–µ–ª—å–Ω—ñ –º—ñ–∂ —Å–æ–±–æ—é.
- –ö—É—Ç –º—ñ–∂ –ø–µ—Ä–ø–µ–Ω–¥–∏–∫—É–ª—è—Ä–æ–º, –ø—Ä–æ–≤–µ–¥–µ–Ω–∏–º –¥–æ –¥–æ—Ç–∏—á–Ω–æ—ó —ñ–∑ –ø–æ—á–∞—Ç–∫—É –∫–æ–æ—Ä–¥–∏–Ω–∞—Ç, —Ç–∞ –ø–æ–ª—è—Ä–Ω–æ—é –≤—ñ—Å—Å—é –≤—Ç—Ä–∏—á—ñ –±—ñ–ª—å—à–∏–π –∑–∞ –ø–æ–ª—è—Ä–Ω–∏–π –∫—É—Ç
 —Ç–æ—á–∫–∏ –¥–æ—Ç–∏–∫—É. –¢–∞–∫–∏–º —á–∏–Ω–æ–º, –ª–µ–º–Ω—ñ—Å–∫–∞—Ç—É –º–æ–∂–Ω–∞ –≤–∏–∫–æ—Ä–∏—Å—Ç–æ–≤—É–≤–∞—Ç–∏ –¥–ª—è —Ç—Ä–∏—Å–µ–∫—Ü—ñ—ó –∫—É—Ç–∞. : —Å—Ç–æ—Ä.156
—Ç–æ—á–∫–∏ –¥–æ—Ç–∏–∫—É. –¢–∞–∫–∏–º —á–∏–Ω–æ–º, –ª–µ–º–Ω—ñ—Å–∫–∞—Ç—É –º–æ–∂–Ω–∞ –≤–∏–∫–æ—Ä–∏—Å—Ç–æ–≤—É–≤–∞—Ç–∏ –¥–ª—è —Ç—Ä–∏—Å–µ–∫—Ü—ñ—ó –∫—É—Ç–∞. : —Å—Ç–æ—Ä.156
- –õ–µ–º–Ω—ñ—Å–∫–∞—Ç–∞ –ë–µ—Ä–Ω—É–ª–ª—ñ –ø–µ—Ä–µ—Ç–∏–Ω–∞—î –≤—ñ—Å—å
 –≤ —Ç–æ—á–∫–∞—Ö
–≤ —Ç–æ—á–∫–∞—Ö
 —Ç–∞
—Ç–∞  .
.
- –ö—Ä–∏–≤–∞ –º–∞—î 2 –º–∞–∫—Å–∏–º—É–º–∏ —ñ 2 –º—ñ–Ω—ñ–º—É–º–∏. –á—Ö –∫–æ–æ—Ä–¥–∏–Ω–∞—Ç–∏:

- –í—ñ–¥—Å—Ç–∞–Ω—å –≤—ñ–¥ –º–∞–∫—Å–∏–º—É–º—É –¥–æ –º—ñ–Ω—ñ–º—É–º—É, —â–æ –∑–Ω–∞—Ö–æ–¥—è—Ç—å—Å—è –ø–æ –æ–¥–Ω—É —Å—Ç–æ—Ä–æ–Ω—É –≤—ñ–¥ —Å–µ—Ä–µ–¥–∏–Ω–Ω–æ–≥–æ –ø–µ—Ä–ø–µ–Ω–¥–∏–∫—É–ª—è—Ä–∞ (–æ—Å—ñ
 –≤ –¥–∞–Ω–æ–º—É –≤–∏–ø–∞–¥–∫—É) –¥–æ—Ä—ñ–≤–Ω—é—î –≤—ñ–¥—Å—Ç–∞–Ω—ñ –≤—ñ–¥ –º–∞–∫—Å–∏–º—É–º—É (—á–∏ –≤—ñ–¥ –º—ñ–Ω—ñ–º—É–º—É) –¥–æ –ø–æ–¥–≤—ñ–π–Ω–æ—ó —Ç–æ—á–∫–∏.
–≤ –¥–∞–Ω–æ–º—É –≤–∏–ø–∞–¥–∫—É) –¥–æ—Ä—ñ–≤–Ω—é—î –≤—ñ–¥—Å—Ç–∞–Ω—ñ –≤—ñ–¥ –º–∞–∫—Å–∏–º—É–º—É (—á–∏ –≤—ñ–¥ –º—ñ–Ω—ñ–º—É–º—É) –¥–æ –ø–æ–¥–≤—ñ–π–Ω–æ—ó —Ç–æ—á–∫–∏.

–õ–µ–º–Ω—ñ—Å–∫–∞—Ç–∞ –≤ —Å–≤–æ—é —á–µ—Ä–≥—É —î –ø–æ–¥–µ—Ä–æ—é —Ä—ñ–≤–Ω–æ–±—ñ—á–Ω–æ—ó –≥—ñ–ø–µ—Ä–±–æ–ª–∏.
- –õ–µ–º–Ω—ñ—Å–∫–∞—Ç–∞ —î –≥–µ–æ–º–µ—Ç—Ä–∏—á–Ω–∏–º –º—ñ—Å—Ü–µ–º —Ç–æ—á–æ–∫, —â–æ —Å–∏–º–µ—Ç—Ä–∏—á–Ω—ñ –∑ —Ü–µ–Ω—Ç—Ä–æ–º —Ä—ñ–≤–Ω–æ–±—ñ—á–Ω–æ—ó –≥—ñ–ø–µ—Ä–±–æ–ª–∏, –ø–æ –≤—ñ–¥–Ω–æ—à–µ–Ω–Ω—é –¥–æ —ó—ó –¥–æ—Ç–∏—á–Ω–∏—Ö. : —Å—Ç–æ—Ä.157
- –ö—ñ–Ω–µ–º–∞—Ç–∏—á–Ω–æ –ª–µ–º–Ω—ñ—Å–∫–∞—Ç—É –º–æ–∂–Ω–∞ –æ—Ç—Ä–∏–º–∞—Ç–∏ —è–∫ —Ç—Ä–∞–µ–∫—Ç–æ—Ä—ñ—é —Å–µ—Ä–µ–¥–∏–Ω–∏ –≤–µ–ª–∏–∫–æ—ó –ª–∞–Ω–∫–∏ —à–∞—Ä–Ω—ñ—Ä–Ω–æ–≥–æ –∞–Ω—Ç–∏–ø–∞—Ä–∞–ª–µ–ª–æ–≥—Ä–∞–º–∞, –ø—Ä–æ—Ç–∏–ª–µ–∂–Ω–∞ –ª–∞–Ω–∫–∞ —è–∫–æ–≥–æ –Ω–µ—Ä—É—Ö–æ–º–æ –∑–∞–∫—Ä—ñ–ø–ª–µ–Ω–∞. : —Å—Ç–æ—Ä.158
- –í—ñ–¥—Ä—ñ–∑–æ–∫ –±—ñ—Å–µ–∫—Ç—Ä–∏—Å–∏ –∫—É—Ç–∞ –º—ñ–∂ —Ñ–æ–∫–∞–ª—å–Ω–∏–º–∏ —Ä–∞–¥—ñ—É—Å–∞–º–∏-–≤–µ–∫—Ç–æ—Ä–∞–º–∏ —Ç–æ—á–∫–∏ –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏ –¥–æ—Ä—ñ–≤–Ω—é—î –≤—ñ–¥—Ä—ñ–∑–∫—É –≤—ñ–¥ —Ü–µ–Ω—Ç—Ä—É –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏ –¥–æ –ø–µ—Ä–µ—Ç–∏–Ω—É —ó—ó –æ—Å—ñ –∑ —Ü—ñ—î—é –±—ñ—Å–µ–∫—Ç—Ä–∏—Å–æ—é. : —Å—Ç–æ—Ä.158
- –ì–µ–æ–º–µ—Ç—Ä–∏—á–Ω–µ –º—ñ—Å—Ü–µ –ø—Ä–æ—î–∫—Ü—ñ–π —Ü–µ–Ω—Ç—Ä—ñ–≤ –∫—Ä–∏–≤–∏–Ω–∏ –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏ –Ω–∞ –≤—ñ–¥–ø–æ–≤—ñ–¥–Ω—ñ —Ä–∞–¥—ñ—É—Å–∏-–≤–µ–∫—Ç–æ—Ä–∏ —î —Ç–∞–∫–æ–∂ –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∞, —Ä—ñ–≤–Ω—è–Ω–Ω—è —è–∫–æ—ó:

–ú–µ—Ç—Ä–∏—á–Ω—ñ —Ö–∞—Ä–∞–∫—Ç–µ—Ä–∏—Å—Ç–∏–∫–∏
–ù–µ—Ö–∞–π –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∞ –ë–µ—Ä–Ω—É–ª–ª—ñ –∑–∞–¥–∞–Ω–∞ —Ä—ñ–≤–Ω—è–Ω–Ω—è–º –≤ –ø–æ–ª—è—Ä–Ω—ñ–π —Å–∏—Å–µ–º—ñ –∫–æ–æ—Ä–¥–∏–Ω–∞—Ç:  . –¢–æ–¥—ñ:
. –¢–æ–¥—ñ:
- –î–æ–≤–∂–∏–Ω–∞ –¥—É–≥–∏ –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏ –º—ñ–∂ —Ç–æ—á–∫–∞–º–∏, —â–æ –≤—ñ–¥–ø–æ–≤—ñ–¥–∞—é—Ç—å –ø–æ–ª—è—Ä–Ω–∏–º –∫—É—Ç–∞–º
 :
:

–í–∏–∫–æ–Ω–∞–≤—à–∏ –∑–∞–º—ñ–Ω—É  , –ø—Ä–∏–≤–æ–¥–∏–º–æ —ñ–Ω—Ç–µ–≥—Ä–∞–ª –¥–æ –≤–∏–¥—É:
, –ø—Ä–∏–≤–æ–¥–∏–º–æ —ñ–Ω—Ç–µ–≥—Ä–∞–ª –¥–æ –≤–∏–¥—É:

де  — неповний еліптичний інтеграл 1-го роду.
— неповний еліптичний інтеграл 1-го роду.
–î–æ–≤–∂–∏–Ω–∞ –≤—Å—ñ—î—ó –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏ –ë–µ—Ä–Ω—É–ª–ª—ñ:

де  — повний еліптичний інтеграл 1-го роду.
— повний еліптичний інтеграл 1-го роду.
- –ü–ª–æ—â–∞ –ø–æ–ª—è—Ä–Ω–æ–≥–æ —Å–µ–∫—Ç–æ—Ä–∞, —â–æ –≤—ñ–¥–ø–æ–≤—ñ–¥–∞—î –∫—É—Ç–∞–º
![{\displaystyle \varphi \in [0,\varphi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b27d2a332b2a150fbbc74fabe56616527446d32) , –ø—Ä–∏
, –ø—Ä–∏  : : —Å—Ç–æ—Ä.159
: : —Å—Ç–æ—Ä.159
 .
.
–ü–µ—Ä–ø–µ–Ω–¥–∏–∫—É–ª—è—Ä, –ø—Ä–æ–≤–µ–¥–µ–Ω–∏–π —ñ–∑ —Ñ–æ–∫—É—Å–∞ –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏ –Ω–∞ —Ä–∞–¥—ñ—É—Å-–≤–µ–∫—Ç–æ—Ä –±—É–¥—å-—è–∫–æ—ó —ó—ó —Ç–æ—á–∫–∏, –¥—ñ–ª–∏—Ç—å –ø–ª–æ—â—É –≤—ñ–¥–ø–æ–≤—ñ–¥–Ω–æ–≥–æ —Å–µ–∫—Ç–æ—Ä–∞ –Ω–∞–≤–ø—ñ–ª. : —Å—Ç–æ—Ä.159
–ü–ª–æ—â–∞ –∫–æ–∂–Ω–æ—ó –ø–µ—Ç–ª—ñ:
 .
.
–¢–æ–±—Ç–æ, –ø–ª–æ—â–∞, –æ–±–º–µ–∂–µ–Ω–∞ –≤—Å—ñ—î—é –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–æ—é –ë–µ—Ä–Ω—É–ª–ª—ñ –¥–æ—Ä—ñ–≤–Ω—é—î –ø–ª–æ—â—ñ –∫–≤–∞–¥—Ä–∞—Ç–∞ –∑—ñ —Å—Ç–æ—Ä–æ–Ω–æ—é  . : —Å—Ç–æ—Ä.159
. : —Å—Ç–æ—Ä.159
- –Ý–∞–¥—ñ—É—Å –∫—Ä–∏–≤–∏–Ω–∏ –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏ –ë–µ—Ä–Ω—É–ª–ª—ñ –≤ –¥–æ–≤—ñ–ª—å–Ω—ñ–π —ó—ó —Ç–æ—á—Ü—ñ –º–æ–∂–Ω–∞ –æ–±—á–∏—Å–ª–∏—Ç–∏ –∑–∞ —Ñ–æ—Ä–º—É–ª–æ—é:
 .
.
де  — радіус-вектор цієї точки.
— радіус-вектор цієї точки.
 — довжина полярної нормалі.
— довжина полярної нормалі.
–¢–æ–±—Ç–æ —Ä–∞–¥—ñ—É—Å –∫—Ä–∏–≤–∏–Ω–∏ –≤ –¥–æ–≤—ñ–ª—å–Ω—ñ–π —Ç–æ—á—Ü—ñ –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏ –≤—Ç—Ä–∏—á—ñ –º–µ–Ω—à–∏–π –∑–∞ –¥–æ–≤–∂–∏–Ω—É –ø–æ–ª—è—Ä–Ω–æ—ó –Ω–æ—Ä–º–∞–ª—ñ –≤ —Ü—ñ–π —Ç–æ—á—Ü—ñ. : —Å—Ç–æ—Ä.156
–ü–æ–±—É–¥–æ–≤–∞
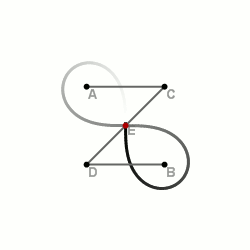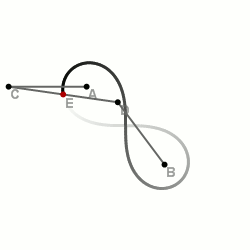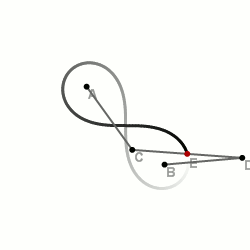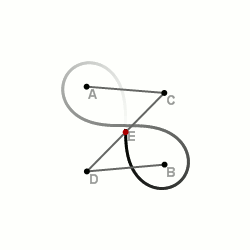 –ü–æ–±—É–¥–æ–≤–∞ –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏ –∑ –¥–æ–ø–æ–º–æ–≥–æ—é —Ç—Ä—å–æ—Ö –≤—ñ–¥—Ä—ñ–∑–∫—ñ–≤.
–ü–æ–±—É–¥–æ–≤–∞ –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏ –∑ –¥–æ–ø–æ–º–æ–≥–æ—é —Ç—Ä—å–æ—Ö –≤—ñ–¥—Ä—ñ–∑–∫—ñ–≤. 
–ó –¥–æ–ø–æ–º–æ–≥–æ—é —Ç—Ä—å–æ—Ö –≤—ñ–¥—Ä—ñ–∑–∫—ñ–≤
–¶–µ –æ–¥–∏–Ω —ñ–∑ –Ω–∞–π–ø—Ä–æ—Å—Ç—ñ—à–∏—Ö —ñ –Ω–∞–π—à–≤–∏–¥—à–∏—Ö —Å–ø–æ—Å–æ–±—ñ–≤, –æ–¥–Ω–∞–∫ –ø–æ—Ç—Ä–µ–±—É—î –Ω–∞—è–≤–Ω–æ—Å—Ç—ñ –¥–æ–¥–∞—Ç–∫–æ–≤–∏—Ö –ø—Ä–∏—Å—Ç–æ—Å—É–≤–∞–Ω—å.
На площині вибираються дві точки —  і
і  — майбутні фокуси лемніскати. Складається спеціальна конструкція із трьох відрізків, скріплених в одну лінію так, щоб отримана лінія могла вільно вигинатися в двох місцях (точки вигину —
— майбутні фокуси лемніскати. Складається спеціальна конструкція із трьох відрізків, скріплених в одну лінію так, щоб отримана лінія могла вільно вигинатися в двох місцях (точки вигину —  та
—Ç–∞  ). –ü—Ä–∏ —Ü—å–æ–º—É –Ω–µ–æ–±—Ö—ñ–¥–Ω–æ –∑–±–µ—Ä—ñ–≥–∞—Ç–∏ –ø—Ä–æ–ø–æ—Ä—Ü—ñ—ó –≤—ñ–¥—Ä—ñ–∑–∫—ñ–≤:
). –ü—Ä–∏ —Ü—å–æ–º—É –Ω–µ–æ–±—Ö—ñ–¥–Ω–æ –∑–±–µ—Ä—ñ–≥–∞—Ç–∏ –ø—Ä–æ–ø–æ—Ä—Ü—ñ—ó –≤—ñ–¥—Ä—ñ–∑–∫—ñ–≤:  . –ö—ñ–Ω—Ü—ñ –ª—ñ–Ω—ñ—ó –∑–∞–∫—Ä—ñ–ø–ª—é—é—Ç—å—Å—è –¥–æ —Ñ–æ–∫—É—Å—ñ–≤. –ü—Ä–∏ –Ω–µ–ø–∞—Ä–∞–ª–ª–µ–ª—å–Ω–æ–º—É –ø–æ–≤–µ—Ä—Ç–∞–Ω–Ω—ñ –≤—ñ–¥—Ä—ñ–∑–∫—ñ–≤ –Ω–∞–≤–∫–æ–ª–æ —Ñ–æ–∫—É—Å—ñ–≤ —Å–µ—Ä–µ–¥–∏–Ω–∞ —Ü–µ–Ω—Ç—Ä–∞–ª—å–Ω–æ–≥–æ –≤—ñ–¥—Ä—ñ–∑–∫–∞ –æ–ø–∏—Å—É–≤–∞—Ç–∏–º–µ –ª–µ–º–Ω—ñ—Å–∫–∞—Ç—É –ë–µ—Ä–Ω—É–ª–ª—ñ.
. –ö—ñ–Ω—Ü—ñ –ª—ñ–Ω—ñ—ó –∑–∞–∫—Ä—ñ–ø–ª—é—é—Ç—å—Å—è –¥–æ —Ñ–æ–∫—É—Å—ñ–≤. –ü—Ä–∏ –Ω–µ–ø–∞—Ä–∞–ª–ª–µ–ª—å–Ω–æ–º—É –ø–æ–≤–µ—Ä—Ç–∞–Ω–Ω—ñ –≤—ñ–¥—Ä—ñ–∑–∫—ñ–≤ –Ω–∞–≤–∫–æ–ª–æ —Ñ–æ–∫—É—Å—ñ–≤ —Å–µ—Ä–µ–¥–∏–Ω–∞ —Ü–µ–Ω—Ç—Ä–∞–ª—å–Ω–æ–≥–æ –≤—ñ–¥—Ä—ñ–∑–∫–∞ –æ–ø–∏—Å—É–≤–∞—Ç–∏–º–µ –ª–µ–º–Ω—ñ—Å–∫–∞—Ç—É –ë–µ—Ä–Ω—É–ª–ª—ñ.
–ë—É–¥—É—î—Ç—å—Å—è –∫–æ–ª–æ —Ä–∞–¥—ñ—É—Å–∞  –∑ —Ü–µ–Ω—Ç—Ä–æ–º –≤ –æ–¥–Ω–æ–º—É —ñ–∑ —Ñ–æ–∫—É—Å—ñ–≤. –Ü–∑ —Å–µ—Ä–µ–¥–∏–Ω–∏
–∑ —Ü–µ–Ω—Ç—Ä–æ–º –≤ –æ–¥–Ω–æ–º—É —ñ–∑ —Ñ–æ–∫—É—Å—ñ–≤. –Ü–∑ —Å–µ—Ä–µ–¥–∏–Ω–∏  —Ñ–æ–∫—É—Å–Ω–æ–≥–æ –≤—ñ–¥—Ä—ñ–∑–∫–∞ –±—É–¥—É—î—Ç—å—Å—è –¥–æ–≤—ñ–ª—å–Ω–∞ —Å—ñ—á–Ω–∞
—Ñ–æ–∫—É—Å–Ω–æ–≥–æ –≤—ñ–¥—Ä—ñ–∑–∫–∞ –±—É–¥—É—î—Ç—å—Å—è –¥–æ–≤—ñ–ª—å–Ω–∞ —Å—ñ—á–Ω–∞  (
( i
i  — точки перетину з колом), і на ній в обидві сторони відкладаються відрізки
— точки перетину з колом), і на ній в обидві сторони відкладаються відрізки  і
—ñ  , —Ä—ñ–≤–Ω—ñ —Ö–æ—Ä–¥—ñ
, —Ä—ñ–≤–Ω—ñ —Ö–æ—Ä–¥—ñ  . –¢–æ—á–∫–∏
. –¢–æ—á–∫–∏  ,
,  –ª–µ–∂–∞—Ç—å –Ω–∞ —Ä—ñ–∑–Ω–∏—Ö –ø–µ—Ç–ª—è—Ö –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏.
–ª–µ–∂–∞—Ç—å –Ω–∞ —Ä—ñ–∑–Ω–∏—Ö –ø–µ—Ç–ª—è—Ö –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∏.
–ó–∞—Å—Ç–æ—Å—É–≤–∞–Ω–Ω—è
- –õ–µ–º–Ω—ñ—Å–∫–∞—Ç–∞ –≤–∏–∫–æ—Ä–∏—Å—Ç–æ–≤—É—î—Ç—å—Å—è —è–∫ –ø–µ—Ä–µ—Ö—ñ–¥–Ω–∞ –ª—ñ–Ω—ñ—è –Ω–∞ –∑–∞–æ–∫—Ä—É–≥–ª–µ–Ω–Ω—è—Ö –º–∞–ª–æ–≥–æ —Ä–∞–¥—ñ—É—Å–∞ –Ω–∞ –∑–∞–ª—ñ–∑–Ω–∏—á–Ω–∏—Ö –∫–æ–ª—ñ—è—Ö –≤ –≥—ñ—Ä–Ω–∏—á—ñ–π –º—ñ—Å—Ü–µ–≤–æ—Å—Ç—ñ, –∞ —Ç–∞–∫–æ–∂ —Ç—Ä–∞–º–≤–∞–π–Ω–∏—Ö –∫–æ–ª—ñ—è—Ö.
- –ï–∫–≤—ñ–ø–æ—Ç–µ–≥—Ü—ñ–π–Ω—ñ –ª—ñ–Ω—ñ—ó –ø–æ–ª—è, —è–∫–µ —Å—Ç–≤–æ—Ä—é—î—Ç—å—Å—è –¥–≤–æ–º–∞ –ø–∞—Ä–∞–ª–µ–ª—å–Ω–∏–º–∏ —Ç–æ–∫–∞–º–∏, —â–æ –ø—Ä–æ—Ç—ñ–∫–∞—é—Ç—å –≤–∑–¥–æ–≤–∂ –Ω–µ—Å–∫—ñ–Ω—á–µ–Ω–Ω–æ –¥–æ–≤–≥–∏—Ö –ø—Ä–æ–≤—ñ–¥–Ω–∏–∫—ñ–≤, –≤ –ø–ª–æ—â–∏–Ω—ñ, —è–∫–∞ –ø–µ—Ä–ø–µ–Ω–¥–∏–∫—É–ª—è—Ä–Ω–∞ –¥–æ –Ω–∏—Ö, –≤ –æ–∫—Ä–µ–º–∏—Ö –≤–∏–ø–∞–¥–∫–∞—Ö —î –ª–µ–º–Ω—ñ—Å–∫–∞—Ç–∞–º–∏.
- Як довів Бонаті, Лемніската є кривою, що володіє тією властивістю, що матеріальна точка великої ваги, виходячи із стану спокою, під дією сили тяжіння переміщається по дузі лемніскати за той самий час, що і по відповідній хорді. При цьому, центр лемніскати збігається з початковим положенням рухомої точки, а її вісь нахилена щодо вертикалі під кутом 45°. : стор.161-162
–î–∏–≤. —Ç–∞–∫–æ–∂
–ü—Ä–∏–º—ñ—Ç–∫–∏
–õ—ñ—Ç–µ—Ä–∞—Ç—É—Ä–∞
–ü–æ—Å–∏–ª–∞–Ω–Ω—è

































![{\displaystyle \varphi \in \left[0,{\frac {\pi }{4}}\right]\cup \left[{\frac {3\pi }{4}},{\frac {5\pi }{4}}\right]\cup \left[{\frac {7\pi }{4}},2\pi \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11be43317f89581ff6fe634be3e11b48e7ffc444)
![{\displaystyle \varphi \in \left[-{\frac {\pi }{4}},{\frac {\pi }{4}}\right]\cup \left[{\frac {3\pi }{4}},{\frac {5\pi }{4}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b3f461a5b8bb336e9bbf64e2c0412f86fcc917b)





















































![{\displaystyle \varphi \in [0,\varphi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b27d2a332b2a150fbbc74fabe56616527446d32)

















































