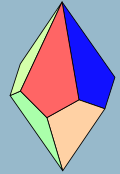
П'ятикутний трапецоедр

Ця стаття не має шаблону-картки. Можливо, потрібен шаблон {{поліедр}}. Ви можете допомогти проєкту, додавши його у статтю.

П'ятикутний трапецоедр
Тип	Двоїстий до однорідного Трапецоедри
Властивості	Напівправильний опуклий, рівногранний, ізоедр
Комбінаторика
Елементи	10 граней; 20 ребер(10 коротких+10 довгих); 12 вершин (10 {3-го степеня}+2{5-го}).
Грані	10 рівних дельтоїдів
Характеристика Ейлера	${\displaystyle \chi =\Gamma -{\hbox{P}}+{\hbox{B}}=2}$
Конфігурація грані	V 5.3.3.3 (послідовне число граней біля кожної вершини навколо грані)
Класифікація
Позначення	• dA5 (в нотації Конвея[en])
Діаграма Коксетера-Динкіна	або (p2p10o) або (p2p5p)
Група симетрії	D5d[en], [2+,10], (2*5), порядок 20 (Діедрична симетрія 5-Антипризми)
Група поворотів	D5, [5,2]+, (522), порядок 10
Двоїстий багатогранник	П'ятикутна антипризма
Розгортка

П'ятикутний трапецоедр (п'ятикутний дельтоедр, п'ятикутний антитегум^[1]) — опуклий напівправильний рівногранний багатогранник, двоїстий до однорідної п'ятикутної антипризми.

Цей багатогранник є напівправильним багатогранником, а отже, володіє такими властивостями:

1. Всі грані є рівними багатокутниками (дельтоїди);
2. Для будь-якої пари граней A і B існує симетрія всього тіла (тобто рух, що складається з поворотів та віддзеркалень), яка переводить A в B.

Він має 10 граней (тобто це десятигранник^[en]), які є конгруентними дельтоїдами з трьома рівними кутами; всі двогранні кути рівні між собою.

Має 12 вершин: в 10 вершинах сходяться своїми більшими кутами по 3 грані (10 вершин 3-го степеня), у 2 вершинах сходяться своїми меншими кутами по 5 граней (2 вершини 5-го степеня).

Вершини п'ятикутного трапецоедра розташовані в чотирьох паралельних площинах.

П'ятикутний трапецоедр є третім у нескінченному ряду рівногранних багатогранників, що є двоїстими до однорідних антипризм.

Його можна розкласти на дві прямі п'ятикутні піраміди і неоднорідну п'ятикутну антипризму між ними. Його також можна розкласти на дві п'ятикутні піраміди та додекаедр між ними.

Тобто 5-трапецоедр можна отримати з правильного додекаедра шляхом нарощення на двох його протилежних гранях п'ятикутних пірамід.

5-трапецоедр також існує у вигляді сферичного багатогранника з 2 вершинами на полюсах і вершинами, що чергуються, які рівномірно розташовані над і під екватором.

У всіх формулах нижче: ${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}\approx 1.618033988749}$ — відношення пропорції «золотого перетину». (послідовність A001622 з Онлайн енциклопедії послідовностей цілих чисел, OEIS).

Відношення між коротким ${\displaystyle l}$ та довгим ${\displaystyle L}$ ребрами 5-трапецоедра: $${\displaystyle {\frac {L}{l}}={\frac {3+{\sqrt {5}}}{2}}=\varphi +1\approx 2.618033988749}$$Гострий кут дельтоїда:

${\displaystyle \alpha =2\pi -3\beta ={\frac {\pi }{5}}rad=36^{\circ }}$;

Тупий кут: ${\displaystyle \beta =\arccos \left({\frac {1}{2}}-\cos \left({\frac {\pi }{5}}\right)\right)={\frac {3\pi }{5}}rad=108^{\circ }}$

Площа грані: ${\displaystyle S={\sqrt {\frac {25+11{\sqrt {15}}}{8}}}\cdot l^{2}={\frac {\varphi +1}{2}}\cdot {\sqrt {\varphi +2}}\cdot l^{2}\approx 2.48989828488278\cdot l^{2}}$

Кількість діагоналей опуклого багатогранника: ${\displaystyle {\binom {B}{2}}-P}$,

де В — кількість вершин, Р — кількість ребер багатогранника.

Для п'ятикутного трапецоедра: ${\displaystyle {\binom {12}{2}}-20={\frac {12}{2}}\cdot {\frac {11}{1}}-20=46}$ діагоналей (20 граневих та 26 просторових).

Діагоналі 5-трапецоедра з довжиною короткого ребра ${\displaystyle l}$
	Граневі діагоналі[2]	${\displaystyle CE={\frac {{\sqrt {5}}+1}{2}}\cdot l=\varphi \cdot l\approx 1.61803398874989\cdot l}$ ${\displaystyle AD={\sqrt {5+2{\sqrt {5}}}}\cdot l=\varphi \cdot {\sqrt {2+\varphi }}\approx 3.07768353717\cdot l}$
	Просторові діагоналі	${\displaystyle CF={\sqrt {2}}\cdot {\frac {{\sqrt {5}}+1}{2}}\cdot l={\sqrt {2}}\cdot \varphi \cdot l\approx 2.28824561127073\cdot l}$ ${\displaystyle GF={\frac {3+{\sqrt {5}}}{2}}\cdot l=\varphi ^{2}\cdot l\approx 2.61803398874989\cdot l}$ ${\displaystyle CK=2~R_{3}={\frac {{\sqrt {3}}+{\sqrt {15}}}{2}}\cdot l={\sqrt {3}}\cdot \varphi \cdot l\approx 2.8025170768881\cdot l}$ ${\displaystyle AB=2~R_{5}={\sqrt {\frac {25+11{\sqrt {15}}}{2}}}\cdot l=(\varphi +1)\cdot {\sqrt {\varphi +2}}\cdot l\approx 4.97979656976556\cdot l}$

Якщо коротке ребро 5-трапецоедра дорівнює ${\displaystyle l}$, то:
Радіус вписаної сфери (дотикається до всіх граней)	${\displaystyle r={\frac {\sin \left({\frac {\pi }{5}}\right)\cdot {\sqrt {\left(\sec ^{2}\left({\frac {\pi }{10}}\right)-4\right)\left(2\cos \left({\frac {\pi }{5}}\right)-3\right)}}}{4\left(4-5~\cos \left({\frac {\pi }{5}}\right)+\cos \left({\frac {2\pi }{5}}\right)\right)}}\cdot l}$	${\displaystyle r={\frac {1}{2}}{\sqrt {\frac {25+11{\sqrt {15}}}{10}}}\cdot l}$	${\displaystyle ={\frac {2\varphi +1}{2{\sqrt {\varphi +2}}}}\cdot l}$	${\displaystyle \approx 1.1135163\cdot l}$
Радіус напіввписаної сфери (дотикається до всіх ребер)	${\displaystyle \rho ={\frac {1}{4}}\csc \left({\frac {\pi }{10}}\right)\cdot {\sqrt {2\cos \left({\frac {\pi }{5}}\right)+1}}\cdot l}$	${\displaystyle \rho ={\frac {3+{\sqrt {5}}}{4}}\cdot l}$	${\displaystyle ={\frac {\varphi +1}{2}}\cdot l}$	${\displaystyle \approx 1.30901699\cdot l}$
Описаної сфери 5-трапецоедр не має
Радіус сфери R3 та R5(відстань від центра до вершин 3-го степеня та, відповідно, 5-го степеня)	= радіусу описаної сфери вписаного додекаедра	${\displaystyle R_{3}={\frac {{\sqrt {15}}+{\sqrt {3}}}{4}}\cdot l}$	${\displaystyle ={\frac {\sqrt {3}}{2}}\cdot \varphi \cdot l}$	${\displaystyle \approx 1.40125853\cdot l}$
	${\displaystyle R_{5}={\frac {1}{8}}\csc ^{3}\left({\frac {\pi }{10}}\right)\cdot \sin \left({\frac {\pi }{5}}\right)\cdot l}$	${\displaystyle R_{5}={\sqrt {\frac {25+11{\sqrt {15}}}{8}}}\cdot l}$	${\displaystyle ={\frac {\varphi +1}{2}}\cdot {\sqrt {\varphi +2}}\cdot l}$	${\displaystyle \approx 2.48989828\cdot l}$
Площа поверхні	${\displaystyle S={\frac {5}{4}}\csc ^{2}\left({\frac {\pi }{10}}\right){\sqrt {1+4~\cos \left({\frac {\pi }{5}}\right)-2\cos \left({\frac {2\pi }{5}}\right)}}\cdot l^{2}}$	${\displaystyle S=5~{\sqrt {\frac {25+11{\sqrt {15}}}{2}}}\cdot l^{2}}$	${\displaystyle =5(\varphi +1)\cdot {\sqrt {\varphi +2}}\cdot l^{2}}$	${\displaystyle \approx 24.898982\cdot l^{2}}$
Об'єм	${\displaystyle V={\frac {5\cot \left({\frac {\pi }{10}}\right)\cdot \csc ^{2}\left({\frac {\pi }{10}}\right)\cdot \left(2\cos \left({\frac {\pi }{5}}\right)+1\right)}{24\cdot {\sqrt {2+2\cos \left({\frac {\pi }{5}}\right)}}}}\cdot l^{3}}$	${\displaystyle V={\frac {5\cdot (11+5{\sqrt {5}})}{12}}\cdot l^{3}}$	${\displaystyle ={\frac {5}{6}}(3\varphi +2)\cdot {\sqrt {\varphi +1}}\cdot l^{3}}$	${\displaystyle \approx 9.2418082\cdot l^{3}}$

Якщо ребро канонічно двоїстої 5-антипризми дорівнює ${\displaystyle a}$, то для 5-трапецоедра справедливі формули[3][4]:
Довжини ребер	${\displaystyle l={\frac {{\sqrt {5}}-1}{2}}\cdot a=(\varphi -1)\cdot a}$ ${\displaystyle L={\frac {{\sqrt {5}}+1}{2}}\cdot a=\varphi \cdot a}$	${\displaystyle \approx 0.6180339\cdot a}$ ${\displaystyle \approx 1.6180339\cdot a}$
Граневі діагоналі	${\displaystyle d=a}$ ${\displaystyle D={\sqrt {\frac {5+{\sqrt {5}}}{2}}}\cdot a}$	${\displaystyle \approx 1.902113\cdot a}$
Площа грані	${\displaystyle S={\frac {1}{2}}\cdot {\sqrt {\frac {5+{\sqrt {5}}}{2}}}\cdot a^{2}}$	${\displaystyle \approx 0.95105651\cdot a^{2}}$
Радіус вписаної сфери (дотикається до всіх граней)	${\displaystyle r={\frac {1}{2}}{\sqrt {\frac {5+2{\sqrt {5}}}{5}}}\cdot a}$	${\displaystyle \approx 0.68819096\cdot a}$
Радіус напіввписаної сфери (дотикається до всіх ребер)	${\displaystyle \rho ={\frac {1+{\sqrt {5}}}{4}}\cdot a={\frac {\varphi }{2}}\cdot a}$	${\displaystyle \approx 0.80901699\cdot a}$
Радіус сфери R3 та R5(відстань від центра до вершин 3-го степеня та відповідно, 5-го степеня)	${\displaystyle R_{3}={\frac {\sqrt {3}}{2}}\cdot a}$	${\displaystyle \approx 0.8660254\cdot a}$
	${\displaystyle R_{5}={\frac {1}{2}}{\sqrt {5+2{\sqrt {5}}}}\cdot a}$	${\displaystyle \approx 1.5388417\cdot a}$
Площа поверхні	${\displaystyle S=5\cdot {\sqrt {\frac {5+{\sqrt {5}}}{2}}}\cdot a^{2}}$	${\displaystyle \approx 9.5105651\cdot a^{2}}$
Об'єм	${\displaystyle V={\frac {5\cdot (3+{\sqrt {5}})}{12}}\cdot a^{3}}$	${\displaystyle \approx 2.18169499\cdot a^{3}}$

Кути багатогранника
Двогранний кут між гранями	${\displaystyle \alpha =\arccos \left(-{\frac {\sqrt {5}}{5}}\right)=2\cdot \arctan \left(\varphi \right)}$	≈ 2.034443935795 rad ≈ 116° 33′ 54.18423748′′
Тілесний кут при вершині 5-го степеня	${\displaystyle \Omega _{5}=2\pi -10\cdot \arcsin \left({\frac {\sqrt {3-{\sqrt {5}}}}{2}}\right)}$${\displaystyle =2\pi -10\cdot \operatorname {arccsc} \left({\sqrt {3+{\sqrt {5}}}}\right)}$	${\displaystyle \Omega _{5}\thickapprox 1.760400835667}$ ср
Тілесний кут при вершині 3-го степеня	${\displaystyle \Omega _{3}=\arccos \left(-{\frac {11{\sqrt {5}}}{25}}\right)=\pi -\arctan \left({\frac {2}{11}}\right)}$	${\displaystyle \Omega _{3}\thickapprox 2.961739153797}$ ср

В теорії графів граф п'ятикутного трапецоедра^[5] — це граф з 12 вершинами та 20 ребрами, що має кістяк 5-трапецоедра.

10 вершин мають степінь 3, 2 вершини мають степінь 5.

Деякі властивості: двочастковий, планарний, багатогранний, досконалий, без трикутників, однозначно розфарбовуваний, простежуваний

Граф є Гамільтоновим і має ${\displaystyle (5+1)(5+2)=42}$  гамільтонових циклів та ${\displaystyle 2\cdot 5\cdot (3\cdot 5^{2}-7\cdot 5+6)=460}$ гамільтонових шляхів.

П'ятикутний трапецоедр належить до нескінченного ряду рівногранних багатогранників, двоїстих однорідним антипризмам.

Родина n-кутних трапецоедрів

• п
• о
• р

Назва трапецоедра	Двокутний трапецоедр	Трикутний трапецоедр	Чотирикутний трапецоедр	П'ятикутний трапецоедр	Шестикутний трапецоедр	Семикутний трапецоедр	Восьмикутний трапецоедр	Десятикутний трапецоедр	Дванадцятикутний трапецоедр	...	Безкінечнокутний трапецоедр
Зображення багатогранника										...
Сферична мозаїка										Зображення плоскої мозаїки
Конфігурація грані	V2.3.3.3	V3.3.3.3	V4.3.3.3	V5.3.3.3	V6.3.3.3	V7.3.3.3	V8.3.3.3	V10.3.3.3	V12.3.3.3	...	V∞.3.3.3

• Henry Martyn Cundy, A. P. Rollett. Mathematical Models. — 2-ге. — Oxford University Press / Clarendon, 1961. — P. 117.

• Generalized formula of uniform polyhedron (trapezohedron) having 2n congruent right kite faces from Academia.edu
• Weisstein, Eric W. Трапецоедр(англ.) на сайті Wolfram MathWorld.
• Pentagonal Trapezohedron (англ.) на сайті dmccooey.com.