Універсальна властивість

У багатьох галузях математики корисну конструкцію часто можна розглядати як «найбільш ефективний розв'язок» певної проблеми. Означення універсальної властивості використовує мову теорії категорій, щоб зробити це твердження точним і вивчати його теоретичними методами.

Універсальні властивості багатьох топологічних конструкцій були описані П'єром Самюелем у 1948 році. Пізніше вони активно використовувалися Бурбакі. Тісно пов'язана концепція спряжених функторів була незалежно запропонована Даніелем Каном у 1958 році. Концепція універсальної властивості широко використовується у багатьох галузях математики. Розуміння конкретних прикладів є важливим для розуміння абстрактного поняття універсальної властивості. Серед найважливіших прикладів зокрема є: прямий добуток і кодобуток, вільна група, група Гротендіка , компактифікація Стоуна — Чеха, тензорний добуток, пряма границя і обернена границя, ядро і коядро, розшарований добуток і розшарований кодобуток, вирівнювач і ковирівнювач.

Перш ніж давати формальне означення, запропонуємо деяку мотивацію для вивчення подібних конструкцій.

• Конкретний опис деякої конструкції може бути довгим і складним але якщо конструкція задовольняє універсальну властивість, часто можна забути про деталі її опису; все, що потрібно для виведення основних її властивостей, вже міститься в універсальній властивості. Доведення при цьому часто стають коротшими і більш елегантними, якщо в них використовується універсальна властивість, а не конкретні деталі побудови. Наприклад, тензорну алгебру векторного простору будується в кілька кроків, тоді як з її універсальну властивість використовувати набагато простіше.
• Універсальної властивості достатньо, щоб визначити об'єкт з точністю до ізоморфізму. Таким чином, з'являється ще один спосіб довести, що два об'єкти ізоморфні, а саме довести, що вони задовольняють однакову універсальну властивість.
• Універсальні властивості поширені в багатьох галузях математики. Вивчивши їх абстрактні властивості, можна отримати інформацію про всі подібні конструкції і уникнути повторення одного і того ж аналізу в кожному конкретному випадку.

Нехай U: D → C — функтор з категорії D в категорію C, а X — об'єкт категорії C. Розглянемо наступні подвійні визначення:

Універсальним морфізмом (або у даному випадку початковим морфізмом чи початковою стрілкою) з X у U називається пара (A, φ), де A — об'єкт категорії D і φ: X → U(A) — морфізм у категорії C, такий що виконується початкова властивість:

• Для будь-якого Y — об'єкта категорії D і f: X → U(Y) — морфізма в категорії C , існує єдиний морфізм g: A → Y такий, що діаграма нижче є комутативною:

Універсальним морфізмом (або у даному випадку термінальним морфізмом або термінальною стрілкою) з U у X називається пара (A, φ), де A — об'єкт категорії D і φ: U(A) → X — морфізм в категорії C, такий що виконується термінальна властивість:

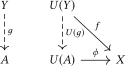
• Для будь-якого Y — об'єкта категорії D і f: U(Y) → X — морфізма категорії C, існує єдиний морфізм g: Y → A, такий що діаграма нижче є комутативною:

Означення універсальних морфізмів можна дати за допомогою ініціальних і термінальних об'єктів кома категорій.

Нехай ${\displaystyle F:C\to D}$ є функтором і ${\displaystyle X}$ — об'єктом категорії ${\displaystyle D}$. За означенням кома категорія ${\displaystyle (X\downarrow F)}$ є категорією у якій

• Об'єктами є пари виду${\displaystyle (B,f:X\to F(B))}$, де ${\displaystyle B}$ є об'єктом категорії ${\displaystyle C}$
• Морфізм із ${\displaystyle (B,f:X\to F(B))}$ у ${\displaystyle (B',f':X\to F(B'))}$ задається морфізмом ${\displaystyle h:B\to B'}$ у ${\displaystyle C}$ для якого діаграма нижче комутує:

Припустимо, що ${\displaystyle (A,u:X\to F(A))}$ є ініціальним об'єктом у ${\displaystyle (X\downarrow F)}$. Тоді для кожного об'єкта ${\displaystyle (A',f:X\to F(A'))}$ існує єдиний морфізм ${\displaystyle h:A\to A'}$ для якого діаграма нижче комутує.

Діаграма з правої сторони є такою ж, як і діаграма в означенні універсального морфізма з ${\displaystyle X}$ у ${\displaystyle F}$. Тому універсальний морфізм із ${\displaystyle X}$ у ${\displaystyle F}$ є еквівалентним ініціальному об'єкту кома категорії ${\displaystyle X\downarrow F}$.

Натомість кома категорією ${\displaystyle (F\downarrow X)}$ є категорія в якій

• Об'єктами є пари виду ${\displaystyle (B,f:F(B)\to X)}$ де ${\displaystyle B}$ є об'єктом категорії ${\displaystyle C}$
• Морфізм із ${\displaystyle (B,f:F(B)\to X)}$ у ${\displaystyle (B',f':F(B')\to X)}$ задається морфізмом ${\displaystyle h:B\to B'}$ у ${\displaystyle C}$ для якого діаграма нижче комутує:

Нехай ${\displaystyle (A,u:F(A)\to X)}$ є термінальним об'єктом у ${\displaystyle (F\downarrow X)}$. Тоді для кожного об'єкта ${\displaystyle (A',f:F(A')\to X)}$ існує єдиний морфізм ${\displaystyle h:A'\to A}$ для якого діаграма нижче комутує.

Діаграма з правої сторони є такою ж, як і діаграма в означенні універсального морфізма з ${\displaystyle F}$ у ${\displaystyle X}$. Тому універсальний морфізм із ${\displaystyle F}$ у ${\displaystyle X}$ є еквівалентним термінальному об'єкту кома категорії ${\displaystyle F\downarrow X}$.

Нехай C — категорія векторних просторів над полем K і D — категорія асоціативних алгебр над K. Розглянемо забуваючий функтор

U : K-Alg → K-Vect

що зіставляє кожній алгебрі відповідний векторний простір.

Для довільного об'єкта X з K-Vect — векторному простору V — можна отримати його тензорну алгебру T(V). А саме, вона характеризується наступними універсальним властивістю:

«Будь-яке лінійне відображення з V у K-алгебру A може бути єдиним чином продовжено до гомоморфізму алгебр T(V) → A.»

Це твердження описує універсальну властивість тензорної алгебри, тобто той факт, що пара (T(V), i), де i : V → T(V) — стандартне вкладення, є початковою стрілкою з векторного простору V у функтор U. Ми отримали функтор T з K-Vect у K-Alg Це означає, що T є лівим спряженим функтором забуваючого функтора U (див. розділ «зв'язок із спряженими функторами»).

Добуток у теорії категорій можна охарактеризувати його універсальним властивістю. А саме: нехай X і Y — об'єкти категорії D, а C — добуток категорій D × D. Визначимо діагональний функтор

Δ : D → D × D

як Δ(X) = (X, X) і Δ(f : X → Y) = (f, f). Тоді якщо (A, φ) - термінальна стрілка з Δ у (X, Y) — об'єкт категорії D × D, то A — об'єкт категорії D, який називається прямим добутком X × Y, а φ — пара проєкцій

π₁ : X × Y → X

π₂ : X × Y → Y.

Для певної універсальної властивості може не існувати об'єкта, який їй задовольняє. Проте якщо такий (A, φ) існує, то він є єдиним із точністю до єдиного ізоморфізму. Перевіримо це для випадку початкової стрілки: якщо (A′, φ′) — інша така пара, то існує єдиний ізоморфізм k: A → A′ такий що φ′ = U(k)φ. Це легко побачити, замінивши (Y, f) з означення початкової властивості на (A′, φ′).

Означення універсальної властивості можна дати багатьма еквівалентними способами. Нехай U — функтор з D у C, X — об'єкт категорії С. Тоді такі формулювання є еквівалентними:

• (A, φ) — початкова стрілка з X в U
• (A, φ) — початковий об'єкт категорії коми ( X v U)
• (A, φ) зображує функтор Hom_C(X, U—),

Подібно можна дати двоїсті формулювання.

Нехай (A₁, φ₁) — початкова стрілка із X₁ у U і (A₂, φ₂) — початкова стрілка з X₂ в U. За початковою властивістю будь-якому морфізму h: X₁ → X₂ відповідає єдиний морфізм g: A₁ → A₂, такий що діаграма нижче є комутативною: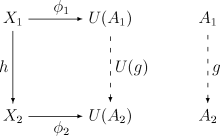

Якщо кожен об'єкт X_i категорії C допускає початкову стрілку в U, то відповідності ${\displaystyle X_{i}\mapsto A_{i}}$ і ${\displaystyle h\mapsto g}$ визначають функтор V з C у D. А відображення φ_i тоді визначають натуральне перетворення з 1_C (тотожний функтор C) у UV . Функтори (V, U) утворюють пару спряжених функторів. Аналогічні твердження є справедливими в двоїстій ситуації термінальних морфізмів з U, у цьому випадку (U, V) будуть парою спряжених функторів.

Насправді всі пари спряжених функторів одержуються із конструкцій такого виду. Нехай F: С → D і G: D → C — пара спряжених функторів з одиницею η і коодиницею ε (див. Статтю спряжені функтори). Тоді існують універсальні морфізми для кожного об'єкта категорій C і D:

• Для кожного об'єкта X з C, (F(X), η_X) — початкова стрілка з X у G. Тобто для всіх f: X → G(Y) існує єдиний g: F(X) → Y, для якого такі діаграми комутують.
• Для кожного об'єкта Y ізD , (G(Y), ε_Y) — термінальна стрілка з F у Y. Тобто для всіх g: F(X) → Y існує єдиний f: X → G(Y), для якого такі діаграми комутують.

Універсальні конструкції є більш загальними, ніж конструкції спряжених функторів: універсальна конструкція схожа на задачу оптимізації, а пара спряжених функторів визначена, тільки якщо ця задача має розв'язок для всіх об'єктів категорії.

• Спряжені функтори

• Borceux, Francis (1994). Handbook of categorical algebra. Volume 1. Encyclopedia of mathematics and its applications. Cambridge University Press. ISBN 0-521-44178-1.
• Leinster, Tom (2014). Basic Category Theory. Cambridge Studies in Advanced Mathematics. Т. 143. Cambridge University Press. ISBN 978-1-107-04424-1.
• Mac Lane, Saunders (1998). Categories for the Working Mathematician. Graduate Texts in Mathematics. Т. 5 (вид. 2nd). Springer-Verlag. ISBN 0-387-98403-8. Zbl 0906.18001.