Спряжені функтори

Спря́жені функтори — пара функторів, що перебувають у певному співвідношенні між собою. Спряжені функтори часто зустрічаються в різноманітних галузях математики.

Неформально, функтори F і G є спряженими, якщо вони задовольняють співвідношенню ${\displaystyle \mathrm {Hom} (F(X),Y)=\mathrm {Hom} (X,G(Y))}$. Тоді F називається лівим спряженим функтором, а G — правим.

Спряжені функтори — один з ключових інструментів теорії категорій, багато важливих математичних конструкцій можна описати як спряжені функтори. В результаті із загальних теорем про спряжені функтори, таких як еквівалентність різних означень, і з того факту, що праві спряжені функтори комутують з границями (а ліві — з кограницями), можуть негайно випливати доведення багатьох цікавих результатів.

Можна сказати, що спряжений функтор є способом вказівки найбільш ефективного розв'язку певної задачі за допомогою стандартного методу. Наприклад, елементарна проблема з теорії кілець — вкладення кільця без одиниці у кільце з одиницею. Найбільш ефективним способом це зробити є додавання в кільце одиниці, всіх елементів, необхідних для виконання аксіом кільця (наприклад, елементи типу r + 1, де r — елемент кільця) без припущення якихось співвідношень в новому кільці, які не потрібні для виконання аксіом. Ця конструкція є стандартною в тому сенсі, що вона працює для будь-якого кільця без одиниці.

Наведений вище опис є дуже розпливчастим але його можна зробити точним, використовуючи мову теорії категорій: конструкція є «найбільш ефективною», якщо вона задовольняє універсальні властивості, і «стандартною» в тому сенсі, що вона задає функтор. Універсальні властивості діляться на початкові і термінальні і оскільки ці поняття є двоїстими, досить розглянути одне з них.

Ідея використання початкової властивості полягає в тому щоб сформулювати проблему в термінах такої допоміжної категорії E, щоб залишилося лише знайти початковий об'єкт E. Таке формулювання має ту перевагу, що завдання «знаходження найбільш ефективного розв'язку» стає чітким і в якомусь сенсі подібним до завданням знаходження екстремуму. Для вибору правильної категорії E іноді потрібно підбирати непрості прийоми: у випадку півкільця R потрібна категорія — це категорія, об'єкти якої — гомоморфізми кілець R → S, де S — деяке кільце з одиницею. Морфізм в E між R → S₁ і R → S₂ — комутативні трикутники виду ( R → S₁ , R → S₂, S₁ → S₂), де S₁ → S₂ — гомоморфізм кілець. Існування морфізма між R → S ₁ і R → S₂ означає, що S₁ є не менш ефективним розв'язком задачі, ніж S₂ : S₂ має більше доданих елементів і (або) більше співвідношень між ними, ніж S₁.

Метод визначає «найбільш ефективний» і «стандартний» розв'язок задач, якщо він задає спряжені функтори.

Існують кілька еквівалентних означень спряжених функторів. Їх еквівалентність є елементарною але не тривіальною.

Означення за допомогою універсальної стрілки ^[⇨] легко сформулювати, воно також найближче до інтуїції з приводу «оптимізаційної задачі».

Означення за допомогою одиниці і коодиниці ^[⇨] є зручно для функторів, часто зустрічаються в алгебрі, тому що використовує формули, які можна перевірити безпосередньо.

Означення за допомогою множин Hom ^[⇨] робить очевидною симетричність означення і прояснює причини для через які функтори називаються «спряженими».

Функтор F: D → C називається лівим спряженим функтором, якщо для кожного об'єкта X категорії C існує термінальний морфізм ε_X з F в X. Це означає, що для кожного X з C можна вибрати об'єкт G(X) з D і морфізм ε_X : F(G(X)) → X, такий, що для кожного об'єкта Y з D і кожного морфізма f: F(Y) → X існує единий морфізм g: Y → G(X), що задовольняє тотожність ε_X ∘ F(g) = f.

Функтор G: C → D називається правим спряженим функтором, якщо для кожного об'єкта Y категорії D існує початковий морфізм з Y в G. Це означає, що для кожного Y з D можна вибрати об'єкт F(Y) з C і морфізм η_Y : Y → G(F(Y)) такий, що кожного об'єкта X з C і морфізма g: Y → G(X) існує єдиний морфізм f: F(Y) → X, такий, що g = G(f) ∘ η_Y.

Функтор F є лівим спряженим для G тоді і тільки тоді, коли G є правим спряженим для F. Однак це не очевидно з означення через універсальну стрілку але очевидно завдяки означенню через одиницю і коодиницю.

Для задання одиниці і коодиниці в категоріях C і D потрібно зафіксувати два функтори F: C ← D, G: C → D і два натуральні перетворення:

${\displaystyle {\begin{aligned}\varepsilon &:FG\to 1_{\mathcal {C}}\\\eta &:1_{\mathcal {D}}\to GF\end{aligned}}}$,

що називаються відповідно коодиницею і одиницею спряження, таких, що композиції

${\displaystyle F{\xrightarrow {\;F\eta \;}}FGF{\xrightarrow {\;\varepsilon F\,}}F}$ і

${\displaystyle G{\xrightarrow {\;\eta G\;}}GFG{\xrightarrow {\;G\varepsilon \,}}G}$

є тотожними перетвореннями 1_F і 1_G функторів F і G відповідно.

У такій ситуації F є лівим спряженим для G і G є правим спряженим для F. Іноді це відношення позначають ${\displaystyle (\varepsilon ,\eta ):F\dashv G}$ або просто ${\displaystyle F\dashv G}$.

У формі рівнянь наведені вище умови на (ε, η) називаються рівняннями коодиниці і одиниці:

${\displaystyle {\begin{aligned}1_{F}&=\varepsilon F\circ F\eta \\1_{G}&=G\varepsilon \circ \eta G\end{aligned}}}$

Розглянемо два функтори F: C ← D і G: C → D . Нехай існує натуральний ізоморфізм:

${\displaystyle \Phi :\mathrm {hom} _{C}(F-,-)\to \mathrm {hom} _{D}(-,G-)}$.

Він визначає сім'ю бієкцій:

${\displaystyle \Phi _{Y,X}:\mathrm {hom} _{C}(FY,X)\to \mathrm {hom} _{D}(Y,GX)}$.

для всіх об'єктів X у C і Y у D .

Тут F називається лівим спряженим для G і G — правим спряженим для F.

Щоб зрозуміти, що мається на увазі під натуральністю Φ, потрібно пояснити, яким чином hom_C(F -, -) і hom_D(-, G -) є функторами. Насправді, вони обидва є біфункторами з D^op×C у Set. В явному вигляді натуральність Φ означає, що для всіх морфізмів f: X → X' у C і морфізма g:Y' → Y у D діаграма нижче комутує: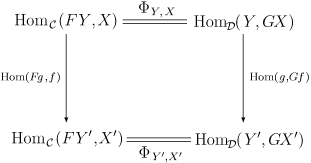

Вертикальні стрілки на діаграмі породжуються композиціями морфізмів. Наприклад, для h у Hom_C(FY, X) за означенням Hom(Fg, f) : Hom_C(FY, X) → Hom_C(FY′, X′) задається як h → f o h o Fg . Подібним є і означення Hom(g, Gf).

В інший спосіб можна описати натуральність так, що для всіх об'єктів X, X' у C і Y, Y' у D, для всіх морфізмів h у Hom_C(FY, X) і f: X → X'

${\displaystyle \Phi _{Y,X'}(f\circ h)=G(f)\circ \Phi _{Y,X}(h)}$

і для всіх морфізмів j у Hom_C(Y , GX) і g: Y' → Y:

${\displaystyle \Phi _{Y',X}^{-1}(j\circ g)=\Phi _{Y,X}^{-1}\circ F(g).}$

Конструкція вільної групи є зручним прикладом для прояснення суті означень. Нехай F: Grp ← Set — функтор, який множині Y зіставляє вільну групу, породжену елементами Y, і G: Grp → Set — забуваючий функтор, що зіставляє групі X її множину-носій. Тоді F — лівий спряжений для G:

Термінальні стрілки: для кожної групи X, група FGX — вільна група, породжена елементами X як множиною. Нехай ${\displaystyle \varepsilon _{X}:FGX\to X}$ — гомоморфізм груп, який переводить породжуючі елементи FGX у відповідні елементи X. Тоді ${\displaystyle (GX,\varepsilon _{X})}$ — термінальний морфізм з F у X, тому що будь-який гомоморфізм з вільної групи FZ в X розкладається через ${\displaystyle \varepsilon _{X}:FGX\to X}$ за допомогою єдиної функції з множини Z в множину X. Це означає, що (F, G) — пара спряжених функторів.

Множині Hom відображення з вільної групи FY у групу X однозначно відповідають відображенням множини Y у множину GX: кожен гомоморфізм однозначно визначається своїми значеннями на породжуючих елементах вільної групи. Прямим обчисленням можна перевірити, що ця відповідність — натуральне перетворення, а тому, пара (F, G) є спряженою.

• Всі вільні об'єкти — результати застосування вільного функтора, який є лівим спряженим для забуваючого функтора.
• добутки, ядра і вирівнювачі — приклади категорних границь. Всі такі функтори є правими спряженими до діагонального функтора. Аналогічно, кодобуток, коядра і ковирівнювачі є кограницями і є лівими спряженими до діагонального функтора.
• Додавання одиниці в кільце без одиниці (приклад з розділу «Мотивація»). Якщо задано кільце без одиниці R, то відповідне йому кільце з одиницею — добуток R×Z, на якому задано Z-білінійний добуток за формулою (r, 0)(0,1) = (0,1)(r, 0) = (r , 0), (r, 0)(s, 0) = (rs, 0), (0,1)(0,1) = (0,1). Побудований функтор є спряженим зліва до забуваючого функтора, що відправляє кільце з одиницею в те ж кільце у категорії кілець, що можуть не мати одиниці.
• Розширення кілець. Нехай R і S — кільця, і ρ: R → S — гомоморфізм кілець . Тоді S можна розглядати як (лівий) R-модуль, і тензорний добуток з S визначає функтор F: R-Mod → S-Mod. Тоді F є спряженим зліва до забуваючого функтора G: S-Mod → R-Mod.
• Тензорні добутки. Якщо R — кільце і M — правий R-модуль, то тензорний добуток з M визначає функтор F: R-Mod → Ab. Функтор G: Ab → R-Mod, визначений як G(A) = hom_Z(M, A) є спряженим справа до F.
• Поле часток. Для категорії Dom_m областей цілісності і ін'єктивних гомоморфізмів, забуваючий функтор Field → Dom_m має лівий спряжений, що зіставляє кожній області цілісності її поле часток.
• Кільця многочленів . Для Ring_* — категорії комутативних кілець із зазначеним елементом і гомоморфізмів, що зберігають зазначений елемент, забуваючий функтор G: Ring_* → Ring має лівий спряжений — він зіставляє кільцю R пару (R[x],x), де R[x] — кільце многочленів з коефіцієнтами з R.
• Забуваючий функтор U: Grp → Mon із категорії груп у групу моноїдів має як лівий спряжений, так і правий спряжений функтори. Лівий спряжений зіставляє моноїду M групу M^gp, яку можна одержати як факторгрупу вільної групи породженої елементами ${\displaystyle [m],\ m\in M,}$по нормальній підгрупі породженій елементами виду ${\displaystyle [mn][n]^{-1}[m]^{-1},\ m,n\in M.}$ Правий спряжений функтор зіставляє моноїду його підгрупу оборотних елементів.
• Абелізація. Забуваючий функтор U: Ab → Grp має лівий спряжений, що називається функтором абелізаціі, який кожній групі G зіставляє факторгрупу по комутанту: G^ab = G/[G, G]. Для групи G її абелізація має універсальну властивість: кожен гомоморфізм ${\displaystyle \varphi }$ із G у абелеву групу A однозначно записується як ${\displaystyle \varphi ={\bar {\varphi }}\ \circ \ \mu ,}$ де ${\displaystyle \mu }$ є відображенням факторизації ${\displaystyle \mu :G\to G^{ab},}$ а ${\displaystyle {\bar {\varphi }}}$ — однозначно визначеним гомоморфізмом абелевих груп.

Бієкцію між множинами hom_Ab(G^ab, A) і hom_Grp(G,U(A)) задається так: гомоморфізму абелевих груп ${\displaystyle \psi :G^{ab}\to A}$ відповідає гомоморфізм ${\displaystyle \psi \ \circ \ \mu ,}$ а гомоморфізму ${\displaystyle \varphi }$ із G у абелеву групу A, визначений вище гомоморфізм ${\displaystyle {\bar {\varphi }}.}$

• Функтор з двома спряженими. Нехай G — функтор, що зіставляє топологічному простору його множину-носій (тобто забуває топологію). У G є лівий спряжений F, який надає множині дискретну топологію, і правий спряжений H, який надає множині тривіальну топологію.
• Надбудова і простір петель. Для даних топологічних просторів X і Y можна побудувати простір [SX,Y] класів гомотопії відображень з надбудови SX у Y. Він є ізоморфним простору [X, ΩY ] класів гомотопії відображень з X у простір петель ΩY, тому функтори надбудови і простору петель є спряженими в гомотопічній категорії топологічних просторів.
• Вкладення G: KHaus → Top категорії компактних гаусдорфових просторів в категорію топологічних просторів має лівий спряжений функтор F: Top → KHaus — компактифікацію Стоуна — Чеха. Коодиниця цієї пари задає неперервне відображення з довільного топологічного простору X у його компактифікацію. Це відображення є вкладенням тоді і тільки тоді, коли X — цілком регулярний простір.

Не кожен функтор G: C → D має лівий або правий спряжений. Якщо C — повна категорія, то згідно теореми про спряжені функтори Петера Фрейда G має лівий спряжений тоді і тільки тоді, коли для будь-якого Y з категорії D існує сім'я морфізмів:

f _i: Y → G(X_i),

де індекси i пробігають множина I, таке, що будь-який морфізм:

h: Y → G(X)

може бути записаний як:

h = G(t) o f_i

для деякого i e I і деякого морфізма:

t: X_i → X e C.

Аналогічне твердження характеризує функтори, що мають правий спряжений.

Якщо функтор F: C ← D має два правих спряжених G і G' , то G' і G є натурально ізоморфними.

Навпаки, якщо F є спряженим зліва до G, і G натурально ізоморфний G' , то F також є спряженим зліва до G '.

Для спряжень можна ввести композиції. Якщо <F, G, ε, η> — спряження між C і D , і <F',G' , ε ', η'> — спряження між D і E, то функтор

${\displaystyle F'\circ F:{\mathcal {C}}\leftarrow {\mathcal {E}}}$

є спряженим зліва до функтора

${\displaystyle G\circ G':{\mathcal {C}}\to {\mathcal {E}}}$.

Можна утворити категорію, об'єктами якої є всі малі категорії, а морфізмами — спряження.

Найбільш важлива властивість спряжених функторів — їх неперервність: кожний функтор, що має лівий спряжений (тобто є правим спряженим), комутує з границями в категорному сенсі. Відповідно, функтор, що має правий спряжений, є конеперервним, тобто комутує з кограницями. Оскільки багато конструкцій є границями або кограницями, з цього відразу випливає кілька наслідків. Наприклад:

• Застосування правого спряженого функтора до добутку дає добуток образів.
• Застосування лівого спряженого функтора до кодобутку дає кодобуток образів.
• Кожний правий спряжений і адитивний функтор між абелевими категоріями є точним зліва.
• Кожний лівий спряжений і адитивний функтор між абелевими категоріями є точним справа.

• Зображуваний функтор
• Функтор Hom
• Категорія (математика)
• Теорія категорій

• И. Букур, А. Деляну Введение в теорию категорий и функторов. — М.: Мир, 1972.
• Adámek, Jiří; Herrlich, Horst; Strecker, George E. (1990). Abstract and Concrete Categories. The joy of cats (PDF). John Wiley & Sons. ISBN 0-471-60922-6. Zbl 0695.18001. Архів оригіналу (PDF) за 21 квітня 2015. Процитовано 19 лютого 2020.
• Borceux, Francis (1994). Handbook of categorical algebra. Volume 1. Encyclopedia of mathematics and its applications. Cambridge University Press. ISBN 0-521-44178-1.
• Leinster, Tom (2014). Basic Category Theory. Cambridge Studies in Advanced Mathematics. Т. 143. Cambridge University Press. ISBN 978-1-107-04424-1.
• Mac Lane, Saunders (1998). Categories for the Working Mathematician. Graduate Texts in Mathematics. Т. 5 (вид. 2nd). Springer-Verlag. ISBN 0-387-98403-8. Zbl 0906.18001.