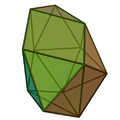
ن؛”角éŒگçگƒç‹€ه±‹é ‚ (و—¥èھï¼ڑن؛”角éŒگçگƒه½¢ه±‹و ¹ [ 1] Disphenocingulum ن¸‰è§’ه½¢ ه’Œ4ه€‹و£و–¹ه½¢çµ„وˆگçڑ„ن؛Œهچپه››é¢é«” [ 2] 詹و£®ه¤ڑé¢é«” çڑ„ه…¶ن¸ن¸€ه€‹ï¼Œç´¢ه¼•ç‚؛J90 [ 3] çگƒç‹€ه±‹é ‚ ن¾†و§‹é€ ,ن½†ه®ƒç„،و³•ç”±وںڈو‹‰هœ–ç«‹é«” (و£ه¤ڑé¢é«”)ه’Œéک؟هں؛ç±³ه¾—ç«‹é«” (هچٹو£ه¤ڑé¢é«”)經éپژهˆ‡ه‰²م€په¢è£œè€Œه¾—ن¾†ï¼Œوک¯è©¹و£®ه¤ڑé¢é«”ن¸çڑ„هں؛وœ¬ç«‹é«”ن¹‹ن¸€م€‚詹و£®ه¤ڑé¢é«”وک¯ه‡¸ه¤ڑé¢é«” ,é¢çڑ†ç”±و£ه¤ڑé‚ٹه½¢çµ„وˆگن½†ن¸چه±¬و–¼ه‡ه‹»ه¤ڑé¢é«”,ه…±وœ‰92種م€‚這ن؛›ç«‹é«”وœ€و—©هœ¨1966ه¹´ç”±è«¾و›¼آ·è©¹و£® [ 4]
ن؛”角éŒگçگƒç‹€ه±‹é ‚ه…±ç”±24ه€‹é¢ م€پ38و¢é‚ٹ ه’Œ16ه€‹é ‚é» çµ„وˆگ[ 5] [ 6] [ 7] [ 8] çگƒç‹€ه±‹é ‚ ن¸‰è§’ه½¢é¢é‡چو–°وژ’هˆ—هگˆن½µè€Œوˆگ,و¯ڈه€‹هژ»é™¤2ه€‹ن¸‰è§’ه½¢é¢çڑ„çگƒç‹€ه±‹é ‚ وœ‰12ه€‹é¢ï¼Œن¸‰è§’ه½¢é¢é‡چو–°وژ’هˆ—هگˆن½µه®Œوˆگه¾Œç‚؛ن؛Œهچپه››é¢é«”م€‚ه…¶è‹±و–‡هگچ稱ه—首م€Œdi-م€چè،¨ç¤؛ه…©ه€‹çگƒç‹€ه±‹é ‚ ,而ه—ه°¾م€Œ-cingulumم€چ(ç‚؛belt(腰ه¸¶ï¼‰çڑ„و‹‰ن¸پèھ)وŒ‡çڑ„وک¯12ه€‹هˆ†ه¸ƒو–¼ه…©ه€‹و£و–¹ه½¢م€Œه±‹é ‚م€چه‘¨هœچçڑ„ن¸‰è§’ه½¢çڑ„è…°ه¸¶ï¼Œه…©è€…ه½¼و¤و—‹è½‰90ه؛¦ن؛’相وژ¥هگˆ[ 7] 諾و›¼آ·è©¹و£® [ 4]
هœ¨çµ„وˆگن؛”角éŒگçگƒç‹€ه±‹é ‚çڑ„24ه€‹é¢ن¸ï¼Œ وœ‰20ه€‹ن¸‰è§’ه½¢é¢ه’Œ4ه€‹و£و–¹ه½¢é¢[ 6] [ 8] [ 8] 5 ]ن¾†è،¨ç¤؛[ 9] 4 ,4]ن¾†è،¨ç¤؛[ 9] [ 8] 2 ,42 ]ن¾†è،¨ç¤؛[ 9]
è‹¥ن¸€ه€‹ن؛”角éŒگçگƒç‹€ه±‹é ‚é‚ٹé•·ç‚؛
a
{\displaystyle a}
è،¨é¢ç©چ
A
{\displaystyle A}
[ 10]
A
=
4
+
5
3
a
2
≈
12.6603
a
2
{\displaystyle A=4+5{\sqrt {3}}a^{2}\approx 12.6603a^{2}}
[ 11] هœ¨92種詹و£®ه¤ڑé¢é«”ن¸ï¼Œوœ‰13種詹و£®ه¤ڑé¢é«”çڑ„ه–®ن½چé‚ٹé•·é«”ç©چ(V /a 3 解وگو•¸ م€‚而ن؛”角éŒگçگƒç‹€ه±‹é ‚ه°±وک¯é€™13種詹و£®ه¤ڑé¢é«”ن¹‹ن¸€م€‚
ç”±و–¼ه…¶é«”ç©چç„،و³•è،¨éپ”ç‚؛解وگو•¸ï¼Œن½†هڈ¯ن»¥ç”¨è؟‘ن¼¼ه€¼è،¨ç¤؛م€‚é‚ٹé•·ç‚؛
a
{\displaystyle a}
V
≈
3.7776453418585752429
a
3
{\displaystyle V\approx 3.7776453418585752429a^{3}}
[ 6] ن¸ٹè؟°é«”ç©چè؟‘ن¼¼ه€¼ç‚؛ن»¥ن¸‹ه¤ڑé …ه¼ڈçڑ„وœ€ه¤§ه¯¦و ¹ï¼ڑ[ 12]
1213025622610333925376 x 24
+ 54451372392730545094656 x 22
x 20
− 4133410366404688544268288 x 18
x 16
− 133907540390420673677230080 x 14
x 12
− 63327534106871321714442240 x 10
x 8
+ 48042947402464500749392128 x 6
x 4
− 3212114716816853362953264 x 2
+ 479556973248657693884401
ن»¤
a
{\displaystyle a}
256
x
12
−
512
x
11
−
1664
x
10
+
3712
x
9
+
1552
x
8
−
6592
x
7
+
1248
x
6
+
4352
x
5
−
2024
x
4
−
944
x
3
+
672
x
2
−
24
x
−
23
{\displaystyle {\begin{aligned}&256x^{12}-512x^{11}-1664x^{10}+3712x^{9}+1552x^{8}-6592x^{7}\\&\quad {}+1248x^{6}+4352x^{5}-2024x^{4}-944x^{3}+672x^{2}-24x-23\end{aligned}}}
ه’Œ
h
=
2
+
8
a
−
8
a
2
{\displaystyle h={\sqrt {2+8a-8a^{2}}}}
c
=
1
−
a
2
{\displaystyle c={\sqrt {1-a^{2}}}}
ه‰‡é‚ٹé•·ç‚؛2çڑ„ن؛”角éŒگçگƒç‹€ه±‹é ‚هڈ¯ن»¥ç”±ن¸‹هˆ—é ‚é»çڑ„軌éپ“ çڑ„ن¸¦é›†هœ¨و²؟xzه¹³é¢ه’Œyzه¹³é¢éڈ،ه°„و‰€ç”¢ç”ںçڑ„ç©؛é–“ه°چ稱群 ن¹‹ç¾¤ن½œç”¨ ن¸‹çµ¦ه‡؛ï¼ڑ[ 13]
(
1
,
2
a
,
h
2
)
,
(
1
,
0
,
2
c
+
h
2
)
,
(
1
+
3
−
4
a
2
c
,
0
,
2
c
−
1
c
+
h
2
)
{\displaystyle \left(1,2a,{\frac {h}{2}}\right),\ \left(1,0,2c+{\frac {h}{2}}\right),\ \left(1+{\frac {\sqrt {3-4a^{2}}}{c}},0,2c-{\frac {1}{c}}+{\frac {h}{2}}\right)}
^ و•´é¢ه‡¸ه¤ڑé¢ن½“مƒ‡مƒ¼م‚؟ . mitani.cs.tsukuba.ac.jp. [2022-09-11 ] . (هژںه§‹ه†…ه®¹هکو،£ ن؛ژ2023-01-14). ^ Santiago Alvarez. Polyhedra in (Inorganic) Chemistry (PDF) . Electronic Supplementary Information for Dalton Transactions. 2005 [2022-09-25 ] . (هژںه§‹ه†…ه®¹هکو،£ (PDF) ن؛ژ2022-01-21). ^ Weisstein, Eric W. (ç¼–). Disphenocingulum . at MathWorld Wolfram Research, Inc. (英è¯ï¼‰ . ^ 4.0 4.1 Johnson, Norman W. Canadian Journal of Mathematics 18 : 169–200, MR 0185507 Zbl 0132.14603 doi:10.4153/cjm-1966-021-8 ^ V.Bulatov. disphenocingulum . [2022-09-11 ] . (هژںه§‹ه†…ه®¹هکو،£ ن؛ژ2022-09-11). ^ 6.0 6.1 6.2 David I. McCooey. Johnson Solids: Disphenocingulum . [2022-09-07 ] . (هژںه§‹ه†…ه®¹هکو،£ ن؛ژ2022-09-11). ^ 7.0 7.1 The Disphenocingulum . qfbox.info. [2022-09-11 ] . (هژںه§‹ه†…ه®¹هکو،£ ن؛ژ2022-12-31). ^ 8.0 8.1 8.2 8.3 Disphenocingulum . polyhedra.tessera.li. [2022-09-11 ] . (هژںه§‹ه†…ه®¹هکو،£ ن؛ژ2023-01-03). ^ 9.0 9.1 9.2 Richard Klitzing. disphenocingulum, dawci . bendwavy.org. [2022-09-11 ] . (هژںه§‹ه†…ه®¹هکو،£ ن؛ژ2022-11-14). ^ Wolfram, Stephen . " Disphenocingulum" Wolfram Alpha : Computational Knowledge Engine, Wolfram Research (英è¯ï¼‰ . ^ Wolfram Research, Inc. Wolfram|Alpha Knowledgebase. Champaign, IL. 2020. PolyhedronData[{"Johnson", 90}, "SurfaceArea"] ^ Wolfram Research, Inc. Wolfram|Alpha Knowledgebase. Champaign, IL. 2020. PolyhedronData[{"Johnson", 90}, "Volume"] ^ Timofeenko, A. V. The non-platonic and non-Archimedean noncomposite polyhedra. Journal of Mathematical Sciences. 2009-10-17, 162 (5): 710–729. ISSN 1072-3374 S2CID 120114341 doi:10.1007/s10958-009-9655-0