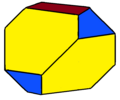
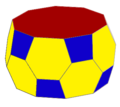
жүӯзЁңеӣӣи§’еҸҚи§’жҹұ пјҲиӢұж–Ү пјҡSnub square antiprismпјүжҳҜи©№жЈ®еӨҡйқўй«” зҡ„е…¶дёӯдёҖеҖӢпјҢе…¶жүҖеј•зӮәJ85 [ 1] жҹҸжӢүең–з«Ӣй«” пјҲжӯЈеӨҡйқўй«” пјүе’Ңйҳҝеҹәзұіеҫ—з«Ӣй«” пјҲеҚҠжӯЈеӨҡйқўй«” пјү經йҒҺеҲҮеүІгҖҒеўһиЈңиҖҢеҫ—дҫҶгҖӮжүӯзЁңеӣӣи§’еҸҚи§’жҹұжҳҜи©№жЈ®еӨҡйқўй«”дёӯзҡ„еҹәжң¬з«Ӣй«”д№ӢдёҖгҖӮи©№жЈ®еӨҡйқўй«”жҳҜеҮёеӨҡйқўй«” пјҢйқўзҡҶз”ұжӯЈеӨҡйӮҠеҪўзө„жҲҗдҪҶдёҚеұ¬ж–јеқҮеӢ»еӨҡйқўй«”пјҢе…ұжңү92зЁ®гҖӮйҖҷдәӣз«Ӣй«”жңҖж—©еңЁ1966е№ҙз”ұи«ҫжӣјВ·и©№жЈ® [ 2]
жүӯзЁңеӣӣи§’еҸҚи§’жҹұе…ұз”ұ26еҖӢйқў гҖҒ40жўқйӮҠ е’Ң16й Ӯй»һ жүҖзө„жҲҗ[ 3] [ 4] [ 5] [ 3] [ 5] й Ӯй»һең– дёӯеҸҜд»Ҙз”Ё[35 ]дҫҶиЎЁзӨә[ 6] [ 5] 4 ,4]дҫҶиЎЁзӨә[ 6]
еҪўеҰӮе…¶еҗҚең°пјҢжүӯзЁңеӣӣи§’еҸҚи§’жҹұеҸҜд»ҘйҖҸйҒҺе°Үеӣӣи§’еҸҚи§’жҹұ еҘ—з”ЁжүӯзЁң и®ҠжҸӣдҫҶж§ӢйҖ гҖӮеңЁж–ҪиҗҠеӨ«еҲ©з¬Ұиҷҹ дёӯеҸҜд»ҘиЎЁзӨәзӮәss{2,8}пјҢе…¶дёӯs{2,8}жҳҜеӣӣи§’еҸҚи§’жҹұ [ 7] иҖғе…Ӣж–Ҝзү№жүӯзЁң пјӣиҖҢеңЁеә·еЁҒжүӯзЁң дёӯпјҢжүӯзЁңеӣӣи§’еҸҚи§’жҹұеҸҜд»ҘйҖҸйҒҺе°Үеӣӣи§’йҢҗеҘ—з”Ёеә·еЁҒжүӯзЁң дҫҶж§ӢйҖ пјҢеңЁеә·еЁҒеӨҡйқўй«”иЎЁзӨәжі• дёӯеҸҜд»ҘиЎЁзӨәзӮәsY4[ 8]
иӢҘдёҖеҖӢжүӯзЁңеӣӣи§’еҸҚи§’жҹұйӮҠй•·зӮә
a
{\displaystyle a}
A
{\displaystyle A}
[ 9]
A
=
(
2
+
6
3
)
a
2
вүҲ
12.39230
a
2
,
{\displaystyle A=\left(2+6{\sqrt {3}}\right)a^{2}\approx 12.39230a^{2},}
[ 10] иҖҢе…¶й«”з©Қ
V
{\displaystyle V}
V
=
Оҫ
a
3
,
{\displaystyle V=\xi a^{3},}
е…¶дёӯ
Оҫ
вүҲ
3.60122
{\displaystyle \xi \approx 3.60122}
531441
x
12
вҲ’
85726026
x
8
вҲ’
48347280
x
6
+
11588832
x
4
+
4759488
x
2
вҲ’
892448.
{\displaystyle 531441x^{12}-85726026x^{8}-48347280x^{6}+11588832x^{4}+4759488x^{2}-892448.}
[ 11]
д»Ө
k
{\displaystyle k}
дёүж¬ЎејҸ зҡ„жӯЈеҜҰж №пјҢзҙ„зӮә
k
вүҲ
0.82354
{\displaystyle k\approx 0.82354}
9
x
3
+
3
3
(
5
вҲ’
2
)
x
2
вҲ’
3
(
5
вҲ’
2
2
)
x
вҲ’
17
3
+
7
6
.
{\displaystyle 9x^{3}+3{\sqrt {3}}\left(5-{\sqrt {2}}\right)x^{2}-3\left(5-2{\sqrt {2}}\right)x-17{\sqrt {3}}+7{\sqrt {6}}.}
е’Ңhзҙ„зӮә
h
вүҲ
1.35374
{\displaystyle h\approx 1.35374}
h
=
2
+
8
+
2
3
k
вҲ’
3
(
2
+
2
)
k
2
4
3
вҲ’
3
k
2
.
{\displaystyle h={\frac {{\sqrt {2}}+8+2{\sqrt {3}}k-3\left(2+{\sqrt {2}}\right)k^{2}}{4{\sqrt {3-3k^{2}}}}}.}
еүҮйӮҠй•·зӮә2зҡ„жүӯзЁңеӣӣи§’еҸҚи§’жҹұзҡ„й Ӯй»һеә§жЁҷз”ұдёӢеҲ—й Ӯй»һзҡ„и»ҢйҒ“ зҡ„дёҰйӣҶеңЁз№һzи»ёж—ӢиҪү90В°е’Ңз№һеһӮзӣҙж–јzи»ёдёҰиҲҮxи»ёеӨҫи§’22.5В°зҡ„зӣҙз·ҡж—ӢиҪү180В°жүҖз”ўз”ҹзҡ„з©әй–“е°ҚзЁұзҫӨ д№ӢзҫӨдҪңз”Ё дёӢзөҰеҮәпјҡ[ 12]
(
1
,
1
,
h
)
,
(
1
+
3
k
,
0
,
h
вҲ’
3
вҲ’
3
k
2
)
{\displaystyle (1,1,h),\,\left(1+{\sqrt {3}}k,0,h-{\sqrt {3-3k^{2}}}\right)}
йЎһдјјзҡ„йҖ ж–№ејҸд№ӢеӨҡйқўй«”йӮ„жңүжүӯзЁңдёүи§’еҸҚи§’жҹұпјҲж–ҪиҗҠеӨ«еҲ©з¬Ұиҷҹпјҡss{2,6}пјүзӮә經йҒҺжүӯзЁңи®ҠжҸӣзҡ„дёүи§’еҸҚи§’жҹұ пјҲеҸҜд»ҘиҰ–зӮәдёҖеҖӢе°ҚзЁұжҖ§ијғдҪҺзҡ„жӯЈе…«йқўй«” пјүпјҢе…¶зөҗжһңзӮәеҒҪдәҢеҚҒйқўй«” пјҲеҸҜд»ҘиҰ–зӮәдёҖеҖӢе°ҚзЁұжҖ§ијғдҪҺзҡ„жӯЈдәҢеҚҒйқўй«” пјүгҖӮеҸҰдёҖеҖӢзӮәжүӯзЁңдә”и§’еҸҚи§’жҹұпјҲж–ҪиҗҠеӨ«еҲ©з¬Ұиҷҹпјҡss{2,10}пјүз”ҡиҮіжҳҜжӣҙй«ҳйӮҠж•ёзҡ„жүӯзЁңеҸҚи§’жҹұпјҢдҪҶе…¶зөҗжһңдёҚжңғжҳҜз”ұжӯЈдёүи§’еҪўж§ӢжҲҗзҡ„еҮёеӨҡйқўй«”гҖӮйӮҠж•ёжӣҙе°‘зҡ„жүӯзЁңдәҢи§’еҸҚи§’жҹұпјҲж–ҪиҗҠеӨ«еҲ©з¬Ұиҷҹпјҡss{2,4}пјүе°ҚжҮүеҸҰдёҖеҖӢи©№жЈ®еӨҡйқўй«”вҖ”вҖ”жүӯзЁңйҚҘеҪўй«” пјҢдҪҶеҝ…й ҲеңЁдәҢи§’еҸҚи§’жҹұдёӯдҝқз•ҷе…©еҖӢйҖҖеҢ–зҡ„е°Қи§’йқўпјҲд»Ҙзҙ…иүІз№ӘиЈҪпјүгҖӮйҖҷдәӣйғҪеҸҜд»ҘиҰ–зӮәдёҖзі»еҲ—жүӯзЁңеҸҚи§’жҹұз„ЎзӘ®еәҸеҲ—зҡ„дёҖй …гҖӮ[ 7]
жүӯзЁңеҸҚи§’жҹұ
е°ҚзЁұжҖ§
D2d , [2+ ,4], (2*2)
D3d , [2+ ,6], (2*3)
D4d , [2+ ,8], (2*4)
D5d , [2+ ,10], (2*5)
еҸҚи§’жҹұ
s{2,4} s{2,6} A3 пјҲйЎөйқўеӯҳжЎЈеӨҮд»Ҫ пјҢеӯҳдәҺдә’иҒ”зҪ‘жЎЈжЎҲйҰҶ пјүs{2,8} A4 пјҲйЎөйқўеӯҳжЎЈеӨҮд»Ҫ пјҢеӯҳдәҺдә’иҒ”зҪ‘жЎЈжЎҲйҰҶ пјүs{2,10} A5 пјҲйЎөйқўеӯҳжЎЈеӨҮд»Ҫ пјҢеӯҳдәҺдә’иҒ”зҪ‘жЎЈжЎҲйҰҶ пјү
жҲӘи§’еҸҚи§’жҹұ
ts{2,6} tA3 пјҲйЎөйқўеӯҳжЎЈеӨҮд»Ҫ пјҢеӯҳдәҺдә’иҒ”зҪ‘жЎЈжЎҲйҰҶ пјүts{2,8} tA4 пјҲйЎөйқўеӯҳжЎЈеӨҮд»Ҫ пјҢеӯҳдәҺдә’иҒ”зҪ‘жЎЈжЎҲйҰҶ пјүts{2,10} tA5 пјҲйЎөйқўеӯҳжЎЈеӨҮд»Ҫ пјҢеӯҳдәҺдә’иҒ”зҪ‘жЎЈжЎҲйҰҶ пјү
е°ҚзЁұжҖ§
D2 , [2,2]+ , (222)
D3 , [3,2]+ , (322)
D4 , [4,2]+ , (422)
D5 , [5,2]+ , (522)
жүӯзЁңеҸҚи§’жҹұ
J84
дәҢеҚҒйқўй«”
J85
еҮ№
sY3 пјҲйЎөйқўеӯҳжЎЈеӨҮд»Ҫ пјҢеӯҳдәҺдә’иҒ”зҪ‘жЎЈжЎҲйҰҶ пјү = HtA3
sY4 пјҲйЎөйқўеӯҳжЎЈеӨҮд»Ҫ пјҢеӯҳдәҺдә’иҒ”зҪ‘жЎЈжЎҲйҰҶ пјү = HtA4
sY5 пјҲйЎөйқўеӯҳжЎЈеӨҮд»Ҫ пјҢеӯҳдәҺдә’иҒ”зҪ‘жЎЈжЎҲйҰҶ пјү = HtA5
ss{2,4} ss{2,6} ss{2,10}
^ Weisstein, Eric W. (зј–). Snub Square Antiprism . at MathWorld Wolfram Research, Inc. пјҲиӢұиҜӯпјү . ^ Johnson, Norman W., Convex polyhedra with regular faces, Canadian Journal of Mathematics 18 : 169вҖ“200, MR 0185507 Zbl 0132.14603 doi:10.4153/cjm-1966-021-8 ^ 3.0 3.1 David I. McCooey. Johnson Solids: Snub square antiprism . [2022-09-07 ] . пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈ дәҺ2022-09-09пјү. ^ The snub square antiprism . qfbox.info. [2022-09-09 ] . пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈ дәҺ2022-09-09пјү. ^ 5.0 5.1 5.2 Snub square antiprism . polyhedra.tessera.li. [2022-09-09 ] . пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈ дәҺ2022-09-09пјү. ^ 6.0 6.1 Richard Klitzing. snub square antiprism, snisquap . bendwavy.org. [2022-09-09 ] . пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈ дәҺ2022-01-25пјү. ^ 7.0 7.1 Jim McNeill. Snub Anti-Prisms . orchidpalms.com. [2019-09-28 ] . пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈ дәҺ2019-03-27пјү. ^ PolyHГ©dronisme . [2022-09-09 ] . пјҲеҺҹе§ӢеҶ…е®№еӯҳжЎЈ дәҺ2022-03-10пјү. ^ Wolfram, Stephen . " Snub square antiprism" Wolfram Alpha : Computational Knowledge Engine, Wolfram Research пјҲиӢұиҜӯпјү . ^ Wolfram Research, Inc., Wolfram|Alpha Knowledgebase, Champaign, IL, 2020, PolyhedronData[{"Johnson", 85}, "SurfaceArea"] ^ Wolfram Research, Inc., Wolfram|Alpha Knowledgebase, Champaign, IL, 2020, MinimalPolynomial[PolyhedronData[{"Johnson", 85}, "Volume"], x] ^ Timofeenko, A. V. The non-Platonic and non-Archimedean noncomposite polyhedra. Journal of Mathematical Science. 2009, 162 (5): 725. S2CID 120114341 doi:10.1007/s10958-009-9655-0