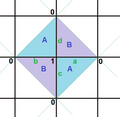
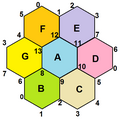
šźőŠľ╣ÚźöŠś»ńŞÇňÇőšÉâÚŁóńŞŐšÜ䊺úňëçňť░ňŹÇňťľ ´╝îňŤášé║šźőŠľ╣ÚźöšÜäšÁÉŠžő´╝łš┤ůŔë▓ŔÖŤšĚÜ´╝ëňĆ»ń╗ąň░ŹŠçëňł░šÉâÚŁóńŞŐňŻóŠłÉšÉâÚŁóÚĹ▓ňÁî´╝łÚ╗ĹšĚÜ´╝ë´╝îńŞŽň░çšÉâÚŁóňłćňë▓ŠłÉ6ňÇőŠşúŠľ╣ňŻó´╝îńŞöŠëÇňŻóŠłÉšÜäšÁÉŠžőňůĚŠťëŔłçŠşúňĄÜÚŁóÚźö šşëňâ╣šÜäň░ŹšĘ▒ŠÇž ňůşÚŁóňŻó Šś»ńŞÇňÇőšÉâÚŁóńŞŐšÜ䊺úňëçňť░ňŹÇňťľ ´╝îňŤášé║ňůşÚŁóňŻóňĆ»ń╗ąÚÇĆÚüÄň░çšÉâÚŁóšöĘ2ňÇőÚáéÚ╗×ňĺî6ŠóŁÚéŐňłćňë▓šé║6ňÇőšÉâÚŁóń║îŔžĺňŻó ŃÇéňťĘŠĽŞňşŞ ńŞş´╝úňëçňť░ňŹÇňťľ ´╝łregular map´╝늜»Šîçň░üھ늍▓ÚŁóńŞŐšÜäň░ŹšĘ▒ÚĹ▓ňÁîňťľŃÇ銍┤š▓żšó║ňť░Ŕ¬¬´╝úňëçňť░ňŹÇňťľŠś»ň░çŠčÉňÇőń║îšÂşŠÁüňŻó ňłćŔžúšé║ňůĚň░ŹšĘ▒ŠÇžń╣őŠőôŠĘŞšŤĄÚŁóšÜäňłćŔžúšÁɊם´╝îńŞöŔę▓ňłćŔžúńŻ┐ňżŚŠëÇŠťëŠĘÖŔĘś ´╝łňÉźŠťëÚ╗×ŃÇüÚéŐŔłçÚŁóšÜäńŞëňůâšÁä´╝ëÚâŻŔâŻňťĘň░ŹšĘ▒ŠÇžńŞŐń╗╗ŠäĆňť░Ŕ«ŐŠĆŤšé║ňůÂń╗ľŠĘÖŔĘś ŃÇéŔłëńżőńżćŔ¬¬´╝îšźőŠľ╣Úźö ň░ŹŠçëšÜäňťľ šÁÉŠžőŠś»ńŞÇňÇőŠşúňëçňť░ňŹÇňťľ´╝îňŤášé║šźőŠľ╣Úźöň░ŹŠçëšÜäšÉâÚŁóÚĹ▓ňÁî šÉâÚŁó ňłćŔžúšé║šö▒6ňÇőŠşúŠľ╣ňŻó šÁ䊳ɚÜäŠőôŠĘŞšŤĄÚŁó´╝îńŞöŠžőŠłÉŔę▓6ňÇőŠşúŠľ╣ňŻóšÜäÚáéÚ╗×ŃÇüÚéŐňĺîÚŁó´╝łňëŹńŞëŔÇůšÜäšÁäňÉłšé║šźőŠľ╣ÚźöšÜäŠĘÖŔĘś ´╝ëňĆ»ń╗ąňťĘšźőŠľ╣ÚźöšÜäň░ŹšĘ▒ŠÇžńŞŐń╗╗ŠäĆňť░Ŕ«ŐŠĆŤšé║ňůÂń╗ľŠĘÖŔĘś´╝îŠĆŤňĆąŔę▒Ŕ¬¬´╝îÚÇÖń║ŤÚáéÚ╗×ŃÇüÚéŐňĺîÚŁóňťĘšë╣ň«ÜŔ╗ŞńŞŐŠŚőŔŻë90ň║ŽňĆ»ń╗ąÚçŹňĺîńŞÇŠČíŃÇé
ŠčɚʫŠäĆšżęńŞŐńżćŔ¬¬´╝úňëçňť░ňŹÇňťľń╣čňĆ»ń╗ąŔŽľšé║ŠčĆŠőëňťľšźőÚźö šÜ䊎éň┐ÁňťĘŠőôŠĘŞňşŞ ńŞŐšÜäńŞÇšĘ«ŠÄĘň╗úŃÇéňť░ňŹÇňťľšÉćŔźľňĆŐňůÂňłćÚí×ŔłçÚ╗ÄŠŤ╝ŠŤ▓ÚŁó šÉćŔźľŃÇüÚŤÖŠŤ▓ň╣żńŻĽ šÉćŔźľňĺîń╝ŻšżůšôŽšÉćŔźľ ŠťëÚŚťŃÇé
Šşúňëçňť░ňŹÇňťľšÜäň«ÜšżęňĺîšáöšęÂÚÇÜňŞŞŠťâÚÇĆÚüÄŠőôŠĘŞŃÇüšżĄŔźľňĺîňťľŔźľšÜäńŞëšĘ«Šľ╣ň╝ĆÚÇ▓ŔíîŃÇé
ňťĘŠőôŠĘŞňşŞ ńŞş´╝îňť░ňŹÇňťľ´╝łmap´╝늜»ň░üÚľëńŞöšĚŐŠ╣Ő ń╣ő2-ŠÁüňŻóšÜä2-Ŕâ×ŔĄçňŻó ňłćŔžúŃÇéňůÂŔÖžŠá╝ňĆ»ń╗ąšöĘŠČžŠő뚥║ŠÇžŠĽ░ ň░Äňç║
χ
(
M
)
=
|
V
|
−
|
E
|
+
|
F
|
{\displaystyle \chi (M)=|V|-|E|+|F|}
2
−
2
g
{\displaystyle 2-2g}
2
−
g
{\displaystyle 2-g}
[ 1] [ 2] [ 3]
ňťĘšżĄŔźľńŞş´╝úňëçňť░ňŹÇňťľšÜäŠÄĺňłŚ Šś»ńŞÇňÇőšö▒ŠĘÖŔĘś ŠžőŠłÉšÜäÚŤćňÉł
Ω
{\displaystyle \Omega }
r 0 , r 1 , r 2 ´╝îńŞŽŠ╗┐ŔÂ│(r0 r2 )2 = IŃÇéňťĘÚÇÖňÇőň«ÜšżęńŞő´╝îÚŁóšé║F = < r0 , r 1 >šÜäŔ╗îÚüô ŃÇüÚéŐšé║E = <r 0 , r 2 >šÜäŔ╗îÚüôŃÇüÚáéÚ╗ךé║V = <r 1 , r 2 >šÜäŔ╗îÚüôŃÇ銍┤ŠŐŻŔ▒íňť░´╝îń╗╗ńŻĽŠşúňëçňť░ňŹÇňťľšÜäŔç¬ňÉőšżĄÚ⯊ś» <2,m,n>-ńŞëŔžĺšżĄšÜäÚŁ×ÚÇÇňîľňÉőňťľŃÇé[ 2]
ňťĘňťľŔźľńŞş´╝îňť░ňŹÇňťľŠś»ńŞÇšĘ«šźőŠľ╣ňťľ ´╝îňůÂňĆ»ń╗ąŔíĘšĄ║šé║ń╗ąńŞëšĘ«ÚíĆŔë▓ŠčôŔë▓šÜäŔĹŚŔë▓ňťľ ´╝łńŞőŠľçń╗ąš┤ůŃÇüÚ╗âŃÇüŔŚŹńŞëšĘ«ÚíĆŔë▓ŔíĘšĄ║ń╣ő´╝ë´╝»ńŞÇšĘ«ÚÇúÚÇÜňťľ´╝îńŞöŠ»ĆňÇőÚáéÚ╗×ÚâŻŔłçŠëÇŠťëÚíĆŔë▓šÜäÚéŐšŤŞŠÄą´╝îÚŁ×Ú╗âŔë▓šÜäÚéŐňç║šĆżÚÇ▒Šťčšé║4ŃÇéňĆŽňĄľ´╝îÚÇ֚ʫňťľń╣芜»ńŞÇšĘ«ň«ÜšżęŠľ╝ÚáéÚ╗×ÚŤćňÉłŠłľŠĘÖŔĘś ÚŤćňÉł
Ω
{\displaystyle \Omega }
ňťľšĚĘšó╝ňťľ
Ω
{\displaystyle \Omega }
[ 4]
ń╗ąńŞőŠś»ńŻŹŠľ╝ŠČžŠő뚥║ŠÇžŠĽ░ šé║Šşúń╣őŠŤ▓ÚŁóńŞŐšÜ䊺úňëçňť░ňŹÇňťľň«îŠĽ┤ňłŚŔíĘ[ 8]
χ g ŠľŻŔÉŐňĄźňłęšČŽŔÖč ÚáéÚ╗×
ÚéŐ
ÚŁó
šżĄ
ÚÜÄŠĽŞ
ňťľ
ňéÖŔĘ╗
2
0
{p,2}
p
p
2
C2 ├Ś Dih p 4p
Cp ňĄÜÚéŐňŻóń║îÚŁóÚźö
2
0
{2,p}
2
p
p
C2 ├Ś Dihp
4p
p -fold K2 ňĄÜÚŁóňŻó
2
0
{3,3}
4
6
4
S 4 24
K4 ŠşúňŤŤÚŁóÚźö
2
0
{4,3}
8
12
6
C2 ├Ś S4
48
K4 ├Ś K2 šźőŠľ╣Úźö
2
0
{3,4}
6
12
8
C2 ├Ś S4
48
K2,2,2 ŠşúňůźÚŁóÚźö
2
0
{5,3}
20
30
12
C2 ├Ś A 5
120
ŠşúňŹüń║îÚŁóÚźö
2
0
{3,5}
12
30
20
C2 ├Ś A5
120
K6 ├Ś K2 Šşúń║îňŹüÚŁóÚźö
1
n1
{2p,2}/2
p
p
1
Dih2p
4p
Cp ňĄÜÚéŐňŻóń║îÚŁóÚźöňŹŐňŻó [ 9]
1
n1
{2,2p}/2
2
p
p
Dih2p
4p
p -fold K2 ňĄÜÚŁóňŻóňŹŐňŻó[ 9]
1
n1
{4,3}/2
4
6
3
S4
24
K4 šźőŠľ╣ÚźöňŹŐňŻó
1
n1
{3,4}/2
3
6
4
S4
24
2-fold K3
ňůźÚŁóÚźöňŹŐňŻó
1
n1
{5,3}/2
10
15
6
A5
60
ńŻęšë╣Šú«ňťľ ňŹüń║îÚŁóÚźöňŹŐňŻó
1
n1
{3,5}/2
6
15
10
A5
60
K6 ń║îňŹüÚŁóÚźöňŹŐňŻó
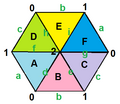
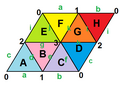
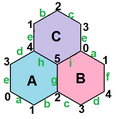
ńŞőňťľň▒ĽšĄ║ń║ć3šĘ«ňťĘŔÖžŠá╝šé║3ń╣őšĺ░ÚŁóńŞŐšÜ䊺úňëçňť░ňŹÇňťľ´╝îńŞŽŠĘÖńŞŐň░ŹŠçëšÜ䊾ŻŔÉŐňĄźňłęšČŽŔÖčŃÇé
Šşúňëçňť░ňŹÇňťľń╣čňĆ»ń╗ąń╗ąšĺ░ňŻóňĄÜÚŁóÚźö ňťôŠč▒ÚźöšÜäňŤŤšÂşŠč▒ b ,c [ 10] ŠľŻŔÉŐňĄźňłęšČŽŔÖč ´╝Ü{3,6}´╝늳ľňůÂň░ŹňüŠşúňůşÚéŐňŻóÚĹ▓ňÁî´╝łŠľŻŔÉŐňĄźňłęšČŽŔÖč ´╝Ü{6,3}´╝ëšÜ䊺úňëçňť░ňŹÇňťľňëçňĆ»ń╗ąŔĘłšé║{3,6}b ,c b ,c [ 11]
Šşúňëçňť░ňŹÇňťľň░ŹŠçëšÜäšĺ░ňŻóňĄÜÚŁóÚźöšÜäň▒ĽÚľőňťľ
1,0 1,1 2,0 2,1 2,2
1,0 1,1 2,0 2,1 2,2
1,0 1,1 2,0 2,1 2,2
ňŻóň╝Ćšé║{4,4}m ,0m }šÜäŠëşŠş¬ŠşúňĄÜÚŁóÚźö ´╝îňůÂń╗úŔíĘŠ»ĆňÇőÚŁóÚ⯊ś»ŠşúŠľ╣ňŻó´╝îńŞöŠ»ĆňÇőÚáéÚ╗×Ú⯊ś»4ňÇőŠşúŠľ╣ňŻóšÜäňůČňů▒ÚáéÚ╗×´╝îńŞŽňŻóŠłÉmÚéŐňŻóňşöŠ┤ךÜäň╣żńŻĽšÁÉŠžőŃÇéňůÂňĆ»ń╗ąšö▒ňŤŤšÂşmŔžĺŠč▒ÚźöŠč▒šÜäÚŁóň╗║ŠžőŃÇé[ 12]
ńŞőňťľšé║{4,4}8,0 ňż×ň╣│ÚŁóŠúőšŤĄň░▒Šžőšé║šĺ░ÚŁóšÜäńŞÇňÇőńżőňşÉŃÇéÚÇÖňÇőńżőňşÉňĆ»ń╗ąńŞŹÚÇĆÚüÄňŤŤšÂşň╣żńŻĽšÁÉŠžőň«îŠłÉň╗║ŠžőŃÇé
^ Conder, Marston; Dobcs├ínyi, Peter, Determination of all regular maps of small genus, Journal of Combinatorial Theory, Series B, 2001, 81 (2): 224ÔÇô242, doi:10.1006/jctb.2000.2008 ^ 2.0 2.1 Nedela, Roman, Maps, Hypermaps, and Related Topics (PDF) , 2007 [2020-08-14 ] , ´╝łňÄčňžőňćůň«╣ňşśŠíú (PDF) ń║Ä2016-03-04´╝ë ^ 3.0 3.1 van Wijk, Jarke J., Symmetric tiling of closed surfaces: visualization of regular maps (PDF) , Proc. SIGGRAPH (ACM Transactions on Graphics), 2009, 28 (3): 12, doi:10.1145/1531326.1531355 ňÄčňžőňćůň«╣ (PDF ) ňşśŠíúń║Ä2011-06-09´╝ë ^ Marston D.E. Conder and Jicheng Ma. Regular maps with simple underlying graphs . Journal of Combinatorial Theory, Series B. 2015, 110 : 1 ÔÇô 18 [2020-08-14 ] . ISSN 0095-8956 doi:10.1016/j.jctb.2014.07.001 ňşśŠíú ń║Ä2020-08-24´╝ë. ^ The hemicube . weddslist.com. [2020-08-14 ] . ´╝łňÄčňžőňćůň«╣ ňşśŠíúń║Ä2019-05-02´╝ë. ^ Gailiunas, Paul; et al. Polyhedral Models of the Projective Plane. Bridges 2018 Conference Proceedings (Tessellations Publishing). 2018: 543ÔÇô546. ^ Weisstein, Eric W. (š╝ľ). Hosohedron . at MathWorld Wolfram Research, Inc. ´╝łŔő▒Ŕ»ş´╝ë . ^ 8.0 8.1 8.2 Coxeter, H. S. M. ; Moser, W. O. J., Generators and Relations for Discrete Groups, Ergebnisse der Mathematik und ihrer Grenzgebiete 14 4th, Springer Verlag, 1980, ISBN 978-0-387-09212-6 ^ 9.0 9.1 S├ęquin, Carlo. Symmetrical immersions of low-genus non-orientable regular maps (PDF) . Berkeley University. [2020-08-14 ] . ´╝łňÄčňžőňćůň«╣ňşśŠíú (PDF) ń║Ä2015-09-23´╝ë. ^ Coxeter 1980[ 8] ^ Coxeter 1980[ 8] ^ Schulte, Egon and Wills, J├Ârg M. On Coxeter's regular skew polyhedra. Discrete mathematics (Elsevier). 1986, 60 : 253ÔÇô262.