笛卡儿坐标系

本条目中，向量與标量分別用粗體與斜體顯示。例如，位置向量通常用 ${\displaystyle \mathbf {r} \,\!}$ 表示；而其大小則用 ${\displaystyle r\,\!}$ 來表示。

笛卡兒坐標系（法語：système de coordonnées cartésiennes；英語：Cartesian coordinate system），也稱直角坐標系（英語：rectangular coordinate system），在數學中是一種正交坐標系，由法國數學家勒內·笛卡兒引入而得名。該坐標系所在的平面稱為直角坐標平面（英語：rectangular coordinate plane）或笛卡兒平面（英語：Cartesian plane）。二維的直角坐標系是由兩條相互垂直、相交於原點的數線構成的。在平面內，任何一點的坐標是根據數軸上對應的點的坐標設定的。在平面內，任何一點與坐標的對應關係，類似於數軸上點與坐標的對應關係。

採用直角坐標，幾何形狀可以用代數公式明確地表達出來。幾何形狀的每一個點的直角坐標必須遵守這個代數公式。例如：直線可以用標準式（一般式）${\displaystyle ax+by+c=0}$、斜截式${\displaystyle y=mx+k}$等式子來表示；以点${\displaystyle (a,b)}$为圆心，${\displaystyle r}$为半径的圓可以用${\displaystyle (x-a)^{2}+(y-b)^{2}=r^{2}}$表示。

法国数学家、哲学家勒内·笛卡兒于1637年在《几何》（La Géométrie）中发表了关于笛卡兒坐标系的研究。皮埃尔·德·费马也独立地发现了这种坐标系，包括三维坐标系，但没有发表。^[1]早在笛卡兒和费马的时代近300年之前，法国主教尼克尔·奥里斯姆就使用了和笛卡兒坐标系类似的构造。^[2]

笛卡兒和费马的坐标系中都仅含一根坐标轴。在1649年弗兰斯·范斯霍滕（英语：Frans van Schooten）及其学生将《几何》译成拉丁文时，为阐释其中的一些想法而引入了一些概念，包括第二根坐标轴。^[3]

笛卡兒坐标系支撑了艾萨克·牛顿和戈特弗里德·莱布尼茨发明的微积分。^[4]后人把用二维坐标描述平面的方法扩展成了向量空间的概念。^[5]

在笛卡兒坐标系之后，人们又创造了更多的坐标系，如平面的极坐标系，以及三维空间的球坐标系和圆柱坐标系。

二維的直角坐標系通常由兩個互相垂直的坐標軸設定，通常分別稱為x-軸和 y-軸；兩個坐標軸的相交點，稱為原點，通常標記為O，既有「零」的意思，又是法语「Origine」的首字母。每一個軸都指向一個特定的方向。這兩個不同線的坐標軸，決定了一個平面，稱為xy-平面，又稱為笛卡兒平面。通常兩個坐標軸只要互相垂直，其指向何方對於分析問題是没有影響的，但習慣性地，x-軸被水平擺放，稱為橫軸，通常指向右方；y-軸被豎直擺放而稱為縱軸，通常指向上方。兩個坐標軸這樣的位置關係，稱為二維的右手坐標系，或右手系。如果把這個右手系畫在一張透明紙片上，則在平面內無論怎樣旋轉它，所得到的都叫做右手系；但如果把紙片翻轉，其背面看到的坐標系則稱為「左手系」。這和照鏡子時左右對調的性質有關。

為了要知道坐標軸的任何一點，離原點的距離。假設，我們可以刻畫數值於坐標軸。那麼，從原點開始，往坐標軸所指的方向，每隔一個單位長度，就刻畫數值於坐標軸。這數值是刻畫的次數，也是離原點的正值整數距離；同樣地，背著坐標軸所指的方向，我們也可以刻畫出離原點的負值整數距離。稱x-軸刻畫的數值為x-坐標，又稱横坐標，稱y-軸刻畫的數值為y-坐標，又稱縱坐標。雖然，在這裏，這兩個坐標都是整數，對應於坐標軸特定的點。按照比例，我們可以推廣至實數坐標和其所對應的坐標軸的每一個點。這兩個坐標就是直角坐標系的直角坐標，標記為${\displaystyle (x,\ y)}$。

任何一個點${\displaystyle P}$在平面的位置，可以用直角坐標來獨特表達。只要從點${\displaystyle P}$畫一條垂直於x-軸的直線。從這條直線與x-軸的相交點，可以找到點${\displaystyle P}$的x-坐標。同樣地，可以找到點${\displaystyle P}$的y-坐標。這樣，我們可以得到點${\displaystyle P}$的直角坐標。

直角坐標系也可以推廣至三維空間與高維空間（higher dimension）。在原本的二維直角坐標系，再添加一個垂直於x-軸，y-軸的坐標軸，稱為z-軸。假若，這三個坐標軸滿足右手定則，則可得到三維的直角坐標系。這z-軸與x-軸，y-軸相互正交於原點。在三維空間的任何一點P，可以用直角坐標${\displaystyle (x,\ y,\ z)}$來表達其位置。

平面直角坐標系的兩個坐標軸將平面分成了四個部分，稱為象限，分別用羅馬數字編號為${\displaystyle I\ (+,\ +)}$，${\displaystyle II\ (-,\ +)}$，${\displaystyle III\ (-,\ -)}$，${\displaystyle IV\ (+,\ -)}$。依照慣例，象限${\displaystyle I}$的兩個坐標都是正值；象限${\displaystyle II}$的x-坐標是負值，y-坐標是正值；象限${\displaystyle III}$的兩個坐標都是負值的；象限${\displaystyle IV}$的x-坐標是正值，y-坐標是負值。所以，象限的編號是按照逆時針方向，從象限${\displaystyle I}$編到象限${\displaystyle IV}$。

三维直角坐标系的三個平面，xy-平面，yz-平面，xz-平面，將三維空間分成了八個部分，稱為卦限 (octant)。通常只有第一卦限有明確的編號，其餘卦限的順序都可能因習慣而不同。第一卦限（${\displaystyle I}$）中每一個點的三個坐標都是正值的。

在平面上笛卡兒坐标为${\displaystyle (x_{1},y_{1})}$和${\displaystyle (x_{2},y_{2})}$的两个点之间的欧几里得距离是：

${\displaystyle d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}.}$

这是毕达哥拉斯定理的笛卡兒坐标版本。在三维空间中，在点${\displaystyle (x_{1},y_{1},z_{1})}$和${\displaystyle (x_{2},y_{2},z_{2})}$之间的距离是：

${\displaystyle d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}},}$

它可用毕达哥拉斯定理的两次连贯应用而得到^[6]。

欧几里得变换或欧几里得移动是欧几里得平面的点集到同一平面上点集的（双射）映射，它保持诸点之间的距离。这种映射（也叫等距映射）有四种类型：平移、旋转、反射和滑移反射^[7]。

平移平面上的一个点集，保持在它们之间的距离，等价于在点集中所有的笛卡兒坐标上增加固定的一对数值${\displaystyle (a,b)}$。就是说，如果所有点的初始坐标是${\displaystyle (x,y)}$，在平移之后它们的坐标将是：

${\displaystyle (x',y')=(x+a,y+b).}$

要绕原点逆时针旋转一个图形${\displaystyle \theta }$度，等价于将所有点的坐标为${\displaystyle (x,y)}$替代为坐标${\displaystyle (x',y')}$，这里有：

${\displaystyle x'=x\cos \theta -y\sin \theta }$

${\displaystyle y'=x\sin \theta +y\cos \theta .}$

因此：

${\displaystyle (x',y')=((x\cos \theta -y\sin \theta \,),(x\sin \theta +y\cos \theta \,)).}$

设一个点的笛卡兒坐标是${\displaystyle (x,y)}$，则${\displaystyle (-x,y)}$是它跨第二坐标轴（y轴）的反射的坐标，如同这个线是个镜子。类似的，${\displaystyle (x,-y)}$是它的跨第一个坐标轴（x轴）的反射的坐标。一般的说，跨过原点与x轴夹角为${\displaystyle \theta }$的直线的反射，等价于将所有点的坐标${\displaystyle (x,y)}$替代为坐标${\displaystyle (x',y')}$，这里有：

${\displaystyle x'=x\cos 2\theta +y\sin 2\theta }$

${\displaystyle y'=x\sin 2\theta -y\cos 2\theta .}$

因此：

${\displaystyle (x',y')=((x\cos 2\theta +y\sin 2\theta \,),(x\sin 2\theta -y\cos 2\theta \,)).}$

滑移反射是跨一个直线的反射和随后在这个直线方向上的平移的复合。可以看出这些运算的次序是无关紧要的（也可以先平移后反射）。

这些平面的欧几里得变换可以使用矩阵以一致的方式来描述。对一个点${\displaystyle (x,y)}$应用欧几里得变换的结果${\displaystyle (x',y')}$给出为公式：

${\displaystyle (x',y')=(x,y)A+b}$

这里的A是一个2×2正交矩阵，而${\displaystyle b=(b_{1},b_{2})}$是任意的数值有序对^[8]；也就是：

${\displaystyle x'=xA_{11}+yA_{21}+b_{1}}$

${\displaystyle y'=xA_{12}+yA_{22}+b_{2},}$

这里的

${\displaystyle A={\begin{pmatrix}A_{11}&A_{12}\\A_{21}&A_{22}\end{pmatrix}}.}$ [注意对点坐标使用行向量则矩阵要写在右侧。]

将是正交的，矩阵${\displaystyle A}$必须有正交的有欧几里得长度1的行，就是：

${\displaystyle A_{11}A_{21}+A_{12}A_{22}=0}$

并且：

${\displaystyle A_{11}^{2}+A_{12}^{2}=A_{21}^{2}+A_{22}^{2}=1.}$

这等价于说${\displaystyle A}$乘以它的转置矩阵必须是单位矩阵。如果这些条件不成立，则公式描述的是这个平面的更一般的仿射变换，假如${\displaystyle A}$的行列式不是零的话。

公式定义了平移，当且仅当${\displaystyle A}$是单位矩阵。变换是绕某个点的旋转，当且仅当${\displaystyle A}$是旋转矩阵，这意味着：

${\displaystyle A_{11}A_{22}-A_{21}A_{12}=1.}$

要得到反射或滑移反射需要：

${\displaystyle A_{11}A_{22}-A_{21}A_{12}=-1.}$

假定不使用平移，变换可以通过简单将有关的变换矩阵相乘来组合起来。

表示笛卡兒坐标的坐标变换的另一种方式是通过仿射变换。在仿射变换中，增加了一个额外维度而所有点对这个额外维度给出数值1。这么做的好处是点平移可以在矩阵A的最后列中指定。在这种方式下，所有欧几里得变换都可处理成矩阵点乘法。仿射变换给出为：

${\displaystyle {\begin{pmatrix}A_{11}&A_{21}&b_{1}\\A_{12}&A_{22}&b_{2}\\0&0&1\end{pmatrix}}{\begin{pmatrix}x\\y\\1\end{pmatrix}}={\begin{pmatrix}x'\\y'\\1\end{pmatrix}}.}$ [注意来自上式的矩阵A是转置的。矩阵在左侧并对点坐标使用列向量。]

使用仿射变换，多个包括平移的不同欧几里得变换，可以简单的通过把它们对应的矩阵相乘而组合起来。

仿射变换的不是欧几里得移动的一个例子是缩放。要使一个图形变大或变小，等价于对所有点的笛卡兒坐标乘以同一个正数${\displaystyle m}$。如果最初图形的点的笛卡兒坐标是${\displaystyle (x,y)}$，缩放后的图形的对应点有坐标：

${\displaystyle (x',y')=(mx,my).}$

如果${\displaystyle m}$大于1，图形变大；如果${\displaystyle m}$在0与1之间，图形变小。

错切变换将平压矩形的对边从而形成平行四边形。水平错切定义为：

${\displaystyle (x',y')=(x+ys,y)}$

垂直错切定义为：

${\displaystyle (x',y')=(x,xs+y)}$

直角坐標系的x-軸與y-軸必須相互垂直。稱包含y-軸的直線為y-線。在二維空間裏，當我們設定了x-軸的位置與方向的同時，我們也設定了y-線的方向。可是，我們仍舊必須選擇，在y-線的以原點為共同點的兩條半線中，哪一條半線的點的坐標是正值的，哪一條是負值的？任何一種選擇決定了xy-平面的取向。

通常，我們選擇的取向是，正值的x-軸横地指向右方，正值的y-軸縱地指向上方。這種取向稱為正值取向、標準取向或右手取向。

右手定則是一種常用的記憶方法，專門用來辨認正值取向：將一隻半握拳的右手放在平面上，大拇指往上指，那麼，其它的手指都從x-軸指向y-軸。

另外一種取向，採用左手定則，專門用來辨認負值取向或左手取向：將一隻半握拳的左手放在xy-平面上，大拇指往上指，那麼，其它的手指都從y-軸指向x-軸。

不論坐標軸是何種取向，將坐標系統做任何角度的旋轉，取向仍舊會保持不變。

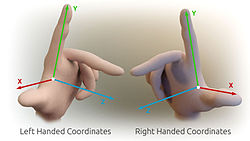
直角坐標系的x-軸、y-軸與z-軸必須相互垂直。稱包含z-軸的直線為z-線。在三維空間裏，當我們設定了x-軸、y-軸的位置與方向的同時，我們也設定了z-線的方向。可是，我們仍舊必須選擇，在z-線以原點為共同點的兩條半線中，哪一條半線的點的坐標是正值的，哪一條是負值的？這兩種不同的坐標系統，稱為右手坐標系與左手坐標系。右手坐標系又稱為標準坐標系或正值坐標系。

右手坐標系這名詞是由右手定則而來的。先將右手的手掌與手指伸直，然後將中指指向往手掌的掌面半空間，與食指呈直角關係。再將大拇指往上指去，與中指、食指都呈直角關係。則大拇指、食指與中指分別表示了右手坐標系的x-軸、y-軸與z-軸。同樣地，用左手也可以表示出左手坐標系。

左侧示意圖展示出一個左手坐標系與一個右手坐標系。因為我們用二維畫面來展示三維物體，會造成扭曲或模稜兩可的圖形。指向下方與右方的軸，也有指向讀者的意思；而位置居於中間的軸，也有指向讀者正在看的方向的意思。平行於xy-平面的紅色圓形曲箭，其紅色箭頭從z-軸前面經過，表示從x-軸往y-軸的旋轉方向。

採用直角坐標系，在三維空間裏，任何一點${\displaystyle P}$都可以用向量來表示。我們可以想像向量為一支羽箭，其箭尾在原點，箭鋒在點${\displaystyle P}$。假若點P的向量是${\displaystyle \mathbf {r} }$，直角坐標是${\displaystyle (x,y,z)}$。那麼，

${\displaystyle \mathbf {r} =x{\hat {\mathbf {i} }}+y{\hat {\mathbf {j} }}+z{\hat {\mathbf {k} }}}$；

其中，單位向量${\displaystyle {\hat {\mathbf {i} }}}$，${\displaystyle {\hat {\mathbf {j} }}}$與${\displaystyle {\hat {\mathbf {k} }}}$分別指向x-軸，y-軸，與z-軸指向的正無窮值方向。

• 廣義坐標
• 正則坐標
• 坐标系
• 正交坐標系

• Descartes, René. Oscamp, Paul J. (trans). Discourse on Method, Optics, Geometry, and Meteorology. 2001.
• Morse PM, Feshbach H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill. 1953: p. 656. ISBN 978-0-07-043316-8.  引文格式1维护：冗余文本 (link)
• Margenau H, Murphy GM. The Mathematics of Physics and Chemistry. New York: D. van Nostrand. 1956: p. 177.  引文格式1维护：冗余文本 (link)
• Korn GA, Korn TM. Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. 1961: pp. 55–79. ASIN B0000CKZX7.  引文格式1维护：冗余文本 (link)
• Sauer R, Szabó I. Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. 1967: p. 94.  引文格式1维护：冗余文本 (link)
• Moon P, Spencer DE. Rectangular Coordinates (x, y, z). Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions corrected 2nd ed., 3rd print ed. New York: Springer-Verlag. 1988: pp. 9–11 (Table 1.01). ISBN 978-0387184302.  引文格式1维护：冗余文本 (link)

• 直角坐標系 （页面存档备份，存于互联网档案馆）
• 直角坐標圖的印表 （页面存档备份，存于互联网档案馆）
• 直角坐標系. PlanetMath. 
• 埃里克·韦斯坦因. 直角坐標系. MathWorld.  （页面存档备份，存于互联网档案馆）