線型代数学 における基底 (きてい、英 : basis )は線型空間 の線型独立 な生成系 である[ 1]
あらゆる線型空間 はそれを生成 できる線型独立 なベクトル 集合を1つ以上持つ。言い換えれば、線型結合で空間の全ベクトルを一意に表せるベクトル集合が常に存在する。そしてそれらベクトルの個数は各線形空間で一意に定まる。つまりあらゆる線形空間は「座標系 」のような定数個の基本要素の線型結合で必ず表現できる[ 2] 基底 と呼ぶ。
基底の取り方に依らない、基底ベクトルの個数(濃度 )は次元 基底の存在定理 で証明される。
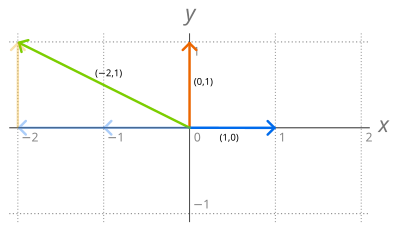
R 2 の標準基底 を示した図。青とオレンジがこの基底の元である。緑のベクトルは基底ベクトルの一次結合で表されており、故にこの三者は線型従属 である。
体 F 上の線型空間 V の基底 B とは、V の線型独立 な部分集合で、V を張る (生成 する)ものを言う[ 1]
より具体的には、V のn個のベクトルの集合B = {v 1 , …, v n v 1 , …, v n
線型独立性
a 1 , …, a n F に対して a 1 v 1 + … + a n v n a 1 = … = a n 全域性
V のどんな元 x も、適当な a 1 , …, a n F を選んで x = a 1 v 1 + … + a n v n を何れも満足することを言う。最後の等式における係数 a i B に関する 座標と呼ばれ、線型独立性により座標は一意的に定まることが分かる。
上記の条件を満たす整数n が存在するとき、その線形空間は有限次元 であるという。そのようなn が存在しないときは無限次元であるという。無限次元線形空間を扱うには、上記定義を一般化して、基底が無限集合となる場合も認めなければならない。すなわち、(有限または無限の)部分集合 B ⊂ V が基底であるとは、
任意の有限部分集合 B 0 ⊆ B が既に述べた意味で線型独立性を持つ。
各 x ∈ V に対して、適当な有限個のスカラー a 1 , …, a n F とベクトル v 1 , …, v n B を選んで x = a 1 v 1 + … + a n v n n は x ごとに違ってよい)。 の二条件を満たすことを言う。最後の式の和は必ず有限和であることに注意。これは、代数的なベクトル空間 の公理だけからは(適当な構造を追加しない限り)極限操作に関する議論が展開できず、無限和 に意味を持たせることができないことによるものである。無限和の場合を許した、別な種類の基底の概念が定義される場合については後述 。
基底ベクトルを特定の「順序」で並べることが便利なことがよくある(例えば、線型写像 の基底に関する変換行列 を考える場合など)。そこで、基底を V を張る線型独立なベクトルの(集合 と考える代わりに)列 (あるいは n -組 )と見た、順序付けられた基底 (ordered basis ) がしばしば用いられる(短く「順序基底」や「順序付き基底」などともいう)。この順序を含めたうえで単に「基底」と呼ぶことも多い。これについても後述 。
有限ベクトル空間
V
{\displaystyle V}
一次独立 な部分集合
S
{\displaystyle S}
V
{\displaystyle V}
S
+
n
=
S
∪
{
v
1
,
.
.
.
,
v
n
∈
span
(
S
)
¯
}
⊂
V
{\displaystyle S_{+n}=S\cup \{{\boldsymbol {v}}_{1},...,{\boldsymbol {v}}_{n}\in {\overline {\operatorname {span} (S)}}\}\subset V}
基底の延長定理 という[ 3] S を基底に延長(拡張)する」という意味を持つ。
この定理は次のように証明できる(概略)。一次独立な
S
⊂
V
{\displaystyle S\subset V}
部分空間
span
(
S
)
{\displaystyle \operatorname {span} (S)}
補集合
span
(
S
)
¯
{\displaystyle {\overline {\operatorname {span} (S)}}}
v
1
{\displaystyle {\boldsymbol {v_{1}}}}
S
{\displaystyle S}
[ 注 1]
S
+
1
=
S
∪
{
v
1
}
{\displaystyle S_{+1}=S\cup \{{\boldsymbol {v_{1}}}\}}
[ 注 2]
span
(
S
+
k
)
¯
{\displaystyle {\overline {\operatorname {span} (S_{+k})}}}
S
+
(
k
+
1
)
{\displaystyle S_{{+}{(k+1)}}}
span
(
S
+
n
)
¯
=
∅
{\displaystyle {\overline {\operatorname {span} (S_{+n})}}=\varnothing }
span
(
S
+
n
)
=
V
{\displaystyle \operatorname {span} (S_{+n})=V}
[ 注 3]
S
+
n
{\displaystyle S_{+n}}
V
{\displaystyle V}
このような基底はほとんど常に複数存在し、一意的に決まることは稀(例えば S が既に基底である場合、S が空集合である場合、V が二元集合である場合など)である。同様の問題として「どのような部分集合 S が基底を含むか」ということを考えることができるが、これには S が V を張ることが必要十分である。この場合、S は複数の異なる基底を含むのが普通である。
有限次元ベクトル空間
V
{\displaystyle V}
生成系
T
⊂
V
{\displaystyle T\subset V}
S
⊂
T
⊂
V
{\displaystyle S\subset T\subset V}
S
⊂
B
⊂
T
{\displaystyle S\subset B\subset T}
B
{\displaystyle B}
[ 4]
この定理は次のように証明できる。
T
{\displaystyle T}
span
(
S
)
{\displaystyle \operatorname {span} (S)}
差集合
T
∖
span
(
S
)
{\displaystyle T\setminus \operatorname {span} (S)}
v
1
∈
(
T
∖
span
(
S
)
)
{\displaystyle {\boldsymbol {v_{1}}}\in (T\setminus \operatorname {span} (S))}
S
{\displaystyle S}
S
+
1
=
S
∪
{
v
1
}
⊂
T
{\displaystyle S_{+1}=S\cup \{{\boldsymbol {v_{1}}}\}\subset T}
T
∖
span
(
S
+
n
)
=
∅
{\displaystyle T\setminus \operatorname {span} (S_{+n})=\varnothing }
span
(
S
+
n
)
=
span
(
T
)
=
V
{\displaystyle \operatorname {span} (S_{+n})=\operatorname {span} (T)=V}
[ 注 4] [ 注 5]
S
+
n
{\displaystyle S_{+n}}
V
{\displaystyle V}
T
{\displaystyle T}
S
⊂
S
+
n
=
B
⊂
T
{\displaystyle S\subset S_{+n}=B\subset T}
{
0
}
{\displaystyle \{{\boldsymbol {0}}\}}
ベクトル空間
V
{\displaystyle V}
V
{\displaystyle V}
B
⊂
V
{\displaystyle B\subset V}
基底の存在定理 という[ 5]
この定理は次のように証明できる(概略)。
V
{\displaystyle V}
V
{\displaystyle V}
S
1
=
{
v
1
|
v
1
≠
0
}
{\displaystyle S_{1}=\{{\boldsymbol {v_{1}}}|{\boldsymbol {v_{1}}}\neq {\boldsymbol {0}}\}}
[ 注 6]
S
1
{\displaystyle S_{1}}
V
{\displaystyle V}
基底の延長定理 [ 注 7]
S
1
{\displaystyle S_{1}}
B
⊂
V
{\displaystyle B\subset V}
無限次元ベクトル空間に対しては、一般には選択公理 が必要である。
ベクトル空間 V の部分集合 B が基底であるためには、以下に挙げるような互いに同値な条件のうちの何れか一つ(従って全部)を満足することが必要十分である。
B は V の極小生成系である。即ち、B は V の生成系であって、かつ B に真に含まれるどの部分集合 も V を生成しない。B は V のベクトルからなる極大線型独立系である。即ち、B は線型独立系であって、かつ B を真に含む V のどの部分集合も線型独立系でない。V に属するどのベクトルも、B に属するベクトルの線型結合としてただ一通りに表される。この基底が順序付けられているとき、この表示の係数はこの基底に関する「座標」を与える(後述 )。任意のベクトル空間は基底を持つ(このことの証明には選択公理 が必要である)。一つのベクトル空間では、全ての基底が同じ濃度 (元の個数)を持ち、その濃度をそのベクトル空間の次元 と呼ぶ。この事実は次元定理 (英語版 ) 超フィルター補題 が必要である)。
a , b がともに実数であるような座標(数ベクトル)(a , b ) 全てからなるベクトル空間 R 2 を考える。このとき、R 2 の任意のベクトル v = (a , b ) は v = a (1,0) + b (0,1) と書けて、e 1 := (1,0) と e 2 := (0,1) は明らかに線型独立だから、{e 1 , e 2 } は R 2 の基底になる。この自然で単純な基底を R 2 の標準基底という。これ以外にも、任意の二つの線型独立なベクトル(例えば (1,1) と (−1,2) など)が、やはり R 2 の基底を成す。
一つの数学的結果が複数のやり方で証明できることは普通であるが、ここでは {(1,1), (−1,2)} が R 2 の基底を成すことの証明を三通りほど挙げてみる。
直接証明
定義に忠実に、二つのベクトル (1,1), (−1,2) が線型独立であることと R 2 を生成することとを示す。
線型独立性
実数 a , b に対して線型関係
a
(
1
,
1
)
+
b
(
−
1
,
2
)
=
(
0
,
0
)
{\displaystyle a(1,1)+b(-1,2)=(0,0)}
a − b , a + 2b ) = (0, 0), 即ち
{
a
−
b
=
0
a
+
2
b
=
0
{\displaystyle {\begin{cases}a-b=0\\a+2b=0\end{cases}}}
b = 0, これを代入して a = 0 を得る。故に線型独立性が示せた。
全域性
二つのベクトル (1,1), (−1,2) が R 2 を生成することを示すには、いま (a , b ) を R 2 の勝手な元として、
r
(
1
,
1
)
+
s
(
−
1
,
2
)
=
(
a
,
b
)
{\displaystyle r(1,1)+s(-1,2)=(a,b)}
r , s の存在を言えばよい。これは即ち、方程式系
{
r
−
s
=
a
r
+
2
s
=
b
{\displaystyle {\begin{cases}r-s=a\\r+2s=b\end{cases}}}
r , s について解けることに他ならない。辺々引いて s が、それを代入して r がそれぞれ
{
s
=
(
b
−
a
)
/
3
r
=
(
b
+
2
a
)
/
3
{\displaystyle {\begin{cases}s=(b-a)/3\\r=(b+2a)/3\end{cases}}}
次元定理による証明
(−1,2) は明らかに (1,1) の定数倍ではないし、(1,1) も明らかに零ベクトル ではないから、二つのベクトル (1,1), (−1,2) は線型独立。これを延長して基底が得られるはずだが、R 2 の次元は 2 だから、{(1,1), (−1,2)} は既に R 2 の基底を成している。
正則行列を用いた証明
二つのベクトル (1,1), (−1,2) を並べてできる行列の行列式 を計算すると
det
(
1
−
1
1
2
)
=
3
{\displaystyle \det \!{\begin{pmatrix}1&-1\\1&2\end{pmatrix}}=3}
正則 である)から、この行列の二つの列ベクトル (1,1), (−1,2) は線型独立。従って R 2 の基底となる。 より一般に、n -次単位行列(対角成分が 1 でそれ以外の成分が 0 の n ×n -行列)の第 i -列ベクトルを e i e 1 , e 2 , ..., e n R n R n R n n であると分かる。この基底を R n 標準基底
V を二つの函数 e t e 2t で生成される実 線型空間とすると、これら二つの函数は線型独立であるから V の基底を成す。次数が高々 2 の多項式全体の成す集合 P2 において、{1, x , x 2 } は標準基底を成す。実数係数多項式 全体の成す線型空間を R [x ] で表せば、無限系列 (1, x , x 2 , …) は R [x ] の基底を成す。従って、R [x ] の次元は、可算濃度 ℵ0 に等しい。
2×2-行列全体の成す集合 M2,2 において、(m ,n )-成分が 1 でそれ以外の成分が 0 の 2×2-行列を E mn E 11 , E 12 , E 21 , E 22 } は標準基底である。 全域的かつ線型独立なベクトルからなる集合を標準基底 から無数に作ることができる。
本ページでは簡単のため、主に基底は単なる集合として扱っており、各ベクトルの順序についての概念は含めていない。ただし、専門的な書籍では基底と呼んだ時にベクトルの順序も含めたうえで意味するとが多い。例えば、その場合には(v 1 , …, v n v n , …, v 1 n -個の自然数を添字 に用いて (v 1 , …, v n 順序基底 (ordered basis)、 標構 あるいは枠 (frame ) とも呼ばれる。
V は体 F 上の n -次元ベクトル空間であるものとする。V の順序基底を一つ選ぶことは、数ベクトル空間 F n V への線型同型写像 φ を一つ選ぶことと等価である。これを見るのに F n
まず、線型同型 φ: F n V が与えられているとき、V の順序基底 (v i 1≤i ≤n を
v i φ (e i i ≤ n で与えることができる。ただし (e i 1≤i ≤n は F n
逆に、順序基底 (v i 1≤i ≤n が与えられているとき、
x
=
x
1
e
1
+
x
2
e
2
+
⋯
+
x
n
e
n
↦
φ
(
x
)
:=
x
1
v
1
+
x
2
v
2
+
⋯
+
x
n
v
n
{\displaystyle x=x_{1}\mathbf {e} _{1}+x_{2}\mathbf {e} _{2}+\cdots +x_{n}\mathbf {e} _{n}\mapsto \varphi (x):=x_{1}v_{1}+x_{2}v_{2}+\cdots +x_{n}v_{n}}
で定まる φ: F n V が線型同型であることを見るのは難しくない。
これら二つの構成が互いに逆になっていることは明らかであるから、V の順序基底とF n V への線型同型との間に一対一対応があることがわかる。
順序基底 (v i V に「座標系」を定める。即ち、ベクトル v ∈ V に対して φ−1 (v ) = (a 1 , a 2 ,...,a n F n a j a j v ) は v = a 1 (v ) v 1 + a 2 (v ) v 2 + ... + a n v ) v n v の座標を与える。
ベクトル v を各成分 a j v ) へ写す各写像は、φ−1 が線型ゆえ、V から F への線型写像になる。即ちこれらは線型汎函数 であり、またこれらは V の双対空間の基底を成し、双対基底 と呼ばれる。
無限次元の実または複素線型空間に関する文脈では、本項でいう意味での基底を表すのに、しばしばハメル基底 (ゲオルク・ハメル (英語版 ) [ 6] 代数基底 という用語が用いられる。(ハメル基底は R の Q -基底を意味することもある。)これは、付加的な構造を備えた無限次元線型空間における別の種類の「基底」の概念との区別のためである。そのような基底の概念で極めて重要なものとしては、ヒルベルト空間 上の正規直交基底 やノルム線型空間 上のシャウダー基底 (英語版 ) マルクシェヴィチ基底 (英語版 )
これらの基底概念に共通する特徴は、全体空間を生成するのに基底ベクトルの無限線型結合までを許すことである。これにはもちろん、無限和が意味を持つような空間(位相線型空間 )を考えることが必要である。位相線型空間は非常に広範なベクトル空間のクラスであり、例えばヒルベルト空間 やバナッハ空間 あるいはフレシェ空間 といったものを含む。
無限次元空間に対してこれら異種の基底が優先されるのは、バナッハ空間においてはハメル基底は「大きすぎる」という事実によるものである。即ち、X が完備 な無限次元ノルム空間(つまりバナッハ空間 )のとき、X の任意のハメル基底が非可算 となることがベールの範疇定理 から従う。先の主張における完備性の仮定は無限次元の仮定同様に重要である。実際、有限次元空間は定義により有限な基底を持つし、また完備でない無限次元ノルム空間で可算なハメル基底を持つものが存在する。有限個の例外を除く 全ての項が 0 となる実数列 全体の成す空間 c 00 にノルム ‖x ‖ = supn x n 標準基底 は可算ハメル基底になる。
例
フーリエ級数 論において、函数系 {1} ∪ {sin(nx ), cos(nx ) : n = 1, 2, 3, …} が、区間 [0, 2π] 上の実(または複素)数値自乗可積分函数、即ち
∫
0
2
π
|
f
(
x
)
|
2
d
x
<
∞
{\displaystyle \int _{0}^{2\pi }|f(x)|^{2}\,dx<\infty }
nx ), cos(nx ) : n = 1, 2, 3, …} は線型独立系であり、かつ区間 [0, 2π] 上自乗可積分な任意の函数 f が適当な実(または複素)係数 a k b k
lim
n
→
∞
∫
0
2
π
|
a
0
+
∑
k
=
1
n
(
a
k
cos
(
k
x
)
+
b
k
sin
(
k
x
)
)
−
f
(
x
)
|
2
d
x
=
0
{\displaystyle \lim _{n\to \infty }\int _{0}^{2\pi }\left|a_{0}+\sum _{k=1}^{n}(a_{k}\cos(kx)+b_{k}\sin(kx))-f(x)\right|^{2}dx=0}
有限 線型結合としては表すことができず、したがってこの「基底」はハメル基底には「ならない」。この空間の任意のハメル基底は、この可算無限にすぎない「基底」よりもはるかに大きいのである(ハメル基底は連続の濃度 をもつ[ 7] 正規直交基底 はフーリエ解析 において本質的である。
関連の深いアフィン空間 、射影空間 、凸集合 、錐 といった空間には関連の深いアフィン基底 [ 8] n -次元アフィン空間に対して一般の位置 にある n +1 点のこと)、射影基底 (本質的にアフィン基底と同じで、ここでは射影空間の、一般の位置にある n +1 点)、凸基底 (多面体の頂点)、錐基底 [ 9]
^
span
(
S
)
{\displaystyle \operatorname {span} (S)}
S
{\displaystyle S}
v
1
∉
span
(
S
)
{\displaystyle {\boldsymbol {v_{1}}}\not \in \operatorname {span} (S)}
^ 一次独立条件式
0
=
c
+
1
v
1
+
∑
s
∈
S
c
s
s
{\displaystyle 0=c_{+1}{\boldsymbol {v_{1}}}+\sum _{{\boldsymbol {s}}\in S}c_{s}{\boldsymbol {s}}}
c
+
1
≠
0
{\displaystyle c_{+1}\neq 0}
v
1
∉
span
(
S
)
{\displaystyle {\boldsymbol {v_{1}}}\not \in \operatorname {span} (S)}
^ 有限ベクトル空間
V
{\displaystyle V}
^
S
+
n
⊆
T
{\displaystyle S_{+n}\subseteq T}
span
(
S
+
n
)
⊋
span
(
T
)
=
V
{\displaystyle \operatorname {span} (S_{+n})\varsupsetneq \operatorname {span} (T)=V}
^ 有限次元ベクトル空間の定義から
T
{\displaystyle T}
^
v
1
≠
0
{\displaystyle {\boldsymbol {v_{1}}}\neq {\boldsymbol {0}}}
c
1
v
1
=
0
{\displaystyle c_{1}{\boldsymbol {v_{1}}}={\boldsymbol {0}}}
c
1
=
0
{\displaystyle c_{1}=0}
^ "生成系内の基底延長定理" でも
S
1
=
{
v
1
∈
T
|
v
1
≠
0
}
{\displaystyle S_{1}=\{{\boldsymbol {v_{1}}}\in T|{\boldsymbol {v_{1}}}\neq {\boldsymbol {0}}\}}
Blass, Andreas (1984), “Existence of bases implies the axiom of choice” , Axiomatic set theory , Contemporary Mathematics volume 31, Providence, R.I.: American Mathematical Society , pp. 31–33, ISBN 0-8218-5026-1 , MR 763890 , http://www.math.lsa.umich.edu/~ablass/bases-AC.pdf Brown, William A. (1991), Matrices and vector spaces , New York: M. Dekker, ISBN 978-0-8247-8419-5 Lang, Serge (1987), Linear algebra , Berlin, New York: Springer-Verlag , ISBN 978-0-387-96412-6
(フランス語) Banach, Stefan (1922), “Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations)” , Fundamenta Mathematicae 3 , ISSN 0016-2736 , http://matwbn.icm.edu.pl/ksiazki/fm/fm3/fm3120.pdf (ドイツ語) Bolzano, Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Considerations of some aspects of elementary geometry) , http://dml.cz/handle/10338.dmlcz/400338 (フランス語) Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques (Elements of history of mathematics) , Paris: Hermann Dorier, Jean-Luc (1995), “A general outline of the genesis of vector space theory” , Historia Mathematica 22 (3): 227–261, doi :10.1006/hmat.1995.1024 , MR 1347828 , http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6WG9-45NJHDR-C&_user=1634520&_coverDate=12%2F31%2F1995&_rdoc=2&_fmt=high&_orig=browse&_srch=doc-info(%23toc%236817%231995%23999779996%23308480%23FLP%23display%23Volume)&_cdi=6817&_sort=d&_docanchor=&_ct=9&_acct=C000054038&_version=1&_urlVersion=0&_userid=1634520&md5=fd995fe2dd19abde0c081f1e989af006 (フランス語) Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur , https://books.google.co.jp/books?id=TDQJAAAAIAAJ&redir_esc=y&hl=ja (ドイツ語) Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik , https://books.google.co.jp/books?id=bKgAAAAAMAAJ&pg=PA1&dq=Die+Lineale+Ausdehnungslehre+ein+neuer+Zweig+der+Mathematik&redir_esc=y&hl=ja Hermann Grassmann. Translated by Lloyd C. Kannenberg. (2000), Extension Theory , Providence, R.I.: American Mathematical Society , ISBN 978-0-8218-2031-5 (ドイツ語) Hamel, Georg (1905), “Eine Basis aller Zahlen und die unstetigen Lösungen der Funktionalgleichung f(x+y)=f(x)+f(y)” , Mathematische Annalen (Leipzig) 60 : 459-462, http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002260395 Hamilton, William Rowan (1853), Lectures on Quaternions , http://historical.library.cornell.edu/cgi-bin/cul.math/docviewer?did=05230001&seq=9 (ドイツ語) Möbius, August Ferdinand (1827), Der Barycentrische Calcul : ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentric calculus: a new utility for an analytic treatment of geometry) , http://mathdoc.emath.fr/cgi-bin/oeitem?id=OE_MOBIUS__1_1_0 Moore, Gregory H. (1995), “The axiomatization of linear algebra: 1875–1940” , Historia Mathematica 22 (3): 262–303, doi :10.1006/hmat.1995.1025 , http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6WG9-45NJHDR-D&_user=1634520&_coverDate=12%2F31%2F1995&_rdoc=3&_fmt=high&_orig=browse&_srch=doc-info(%23toc%236817%231995%23999779996%23308480%23FLP%23display%23Volume)&_cdi=6817&_sort=d&_docanchor=&_ct=9&_acct=C000054038&_version=1&_urlVersion=0&_userid=1634520&md5=4327258ef37b4c293b560238058e21ad (イタリア語) Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva , Turin
Weisstein, Eric W. "Basis" . mathworld.wolfram.com (英語).