ńÉåµā│µ░ŚõĮōŃü«ńŖȵģŗµ¢╣ń©ŗÕ╝Å
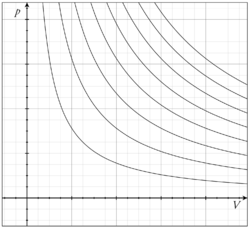 ńÉåµā│µ░ŚõĮōŃü«ńŖȵģŗµ¢╣ń©ŗÕ╝Å’╝łŃéŖŃüØŃüåŃüŹŃü¤ŃüäŃü«ŃüśŃéćŃüåŃü¤ŃüäŃü╗ŃüåŃü”ŃüäŃüŚŃüŹŃĆüĶŗ▒Ķ¬×: ideal gas law’╝ēŃü©Ńü»ŃĆüµ░ŚõĮōŃü«µī»ŃéŗĶł×ŃüäŃéÆńÉåµā│Õī¢ŃüŚŃü¤ńŖȵģŗµ¢╣ń©ŗÕ╝ÅŃü¦ŃüéŃéŗŃĆé Ńü¬ŃüŖŃĆüńÉåµā│µ░ŚõĮōŃü»ŃĆüŃüōŃü«ńŖȵģŗµ¢╣ń©ŗÕ╝ÅŃü½ÕŠōŃüåŃüīŃĆüŃüØŃü«µī»ŃéŗĶł×ŃüäŃü»ńŖȵģŗµ¢╣ń©ŗÕ╝ÅŃüĀŃüæŃü¦Ńü»µ▒║ŃüŠŃéēŃüÜŃĆüµ»öńå▒Õ«╣ķćÅŃü«Õ«ÜµĢ░µĆ¦ŃüīĶ”üµ▒éŃüĢŃéīŃéŗŃĆé µ¢╣ń©ŗÕ╝Åńå▒ÕŖøÕŁ”µĖ®Õ║” TŃĆüÕ£¦ÕŖø p Ńü«õĖŗŃü¦ŃĆüńē®Ķ│¬ķćÅ n Ńü«ńÉåµā│µ░ŚõĮōŃüīÕŹĀŃéüŃéŗõĮōń®Ź V Ńüī
Ńü¦õĖÄŃüłŃéēŃéīŃéŗŃĆéŃüōŃüōŃü¦õ┐éµĢ░ R Ńü»ŃāóŃā½µ░ŚõĮōիܵĢ░Ńü¦ŃüéŃéŗŃĆé ŃüōŃü«Õ╝ÅŃüīńÉåµā│µ░ŚõĮōŃü«ńŖȵģŗµ¢╣ń©ŗÕ╝ÅŃü¦ŃüéŃéŖŃĆüŃā£ŃéżŃā½Ńü«µ│ĢÕēćŃĆüŃéĘŃāŻŃā½Ńā½Ńü«µ│ĢÕēć’╝łŃüéŃéŗŃüäŃü»ÕÉłŃéÅŃüøŃü”Ńā£ŃéżŃā½’╝ØŃéĘŃāŻŃā½Ńā½Ńü«µ│ĢÕēć’╝ēŃü©õĮōń®ŹŃü«ńż║ķćÅµĆ¦ŃüŗŃéēÕ░ÄŃüŗŃéīŃéŗŃĆé Õ«¤Õ£©µ░ŚõĮōŃü«ÕĀ┤ÕÉłŃü»ŃĆüµ░ŚõĮōŃü»Ķ┐æõ╝╝ńÜäŃü½ŃüōŃü«µ¢╣ń©ŗÕ╝ÅŃü½ÕŠōŃüäŃĆüÕ╝ÅŃü«µ£ēÕŖ╣µĆ¦Ńü»µ░ŚõĮōŃü«Õ»åÕ║”Ńüī0Ńü½Ķ┐æŃüźŃüŹ’╝łõĮÄÕ£¦Ńü½Ńü¬ŃéŖ’╝ēŃĆüŃüŗŃüżķ½śµĖ®Ńü½Ńü¬ŃéŗŃü½ŃüżŃéīŃü”ķ½śŃüŠŃéŗŃĆé õĮĢµĢģŃü¬ŃéēŃĆüÕ»åÕ║”Ńüī0Ńü½Ķ┐æõ╗śŃüæŃü░ŃĆüÕłåÕŁÉŃü«ķüŗÕŗĢŃü½ķÜøŃüŚŃĆüŃüŖõ║ÆŃüäŃüīŃüČŃüżŃüŗŃéēŃüÜŃü½ŃĆüÕłåÕŁÉĶć¬Ķ║½Ńü«õĮōń®ŹŃüīńäĪĶ”¢Ńü¦ŃüŹŃéŗŃéłŃüåŃü½Ńü¬ŃéŗŃĆéŃüŠŃü¤ŃĆüķ½śµĖ®Ńü½Ńü¬ŃéŗŃüōŃü©Ńü½ŃéłŃüŻŃü”ŃĆüÕłåÕŁÉŃü«ķüŗÕŗĢŃüīķ½śķƤŃü½Ńü¬ŃéŖŃĆüÕłåÕŁÉķ¢ōÕŖø’╝łŃāĢŃéĪŃā│ŃāćŃā½Ńā»Ńā╝Ńā½Ńé╣ÕŖø’╝ēŃüīńäĪĶ”¢Õć║µØźŃéŗŃéłŃüåŃü½Ńü¬ŃéŗŃüŗŃéēŃü¦ŃüéŃéŗŃĆé Ķ½ĖµĆ¦Ķ│¬ńÉåµā│µ░ŚõĮōŃü«ńŖȵģŗµ¢╣ń©ŗÕ╝ÅŃüŗŃéēÕ░ÄŃüŗŃéīŃéŗµĆ¦Ķ│¬Ńü©ŃüŚŃü”õ╗źõĖŗŃü«ŃééŃü«ŃüīŃüéŃéŗŃĆéŃüōŃéīŃéēŃü»µ»öńå▒Õ«╣ķćÅŃü«Õ«ÜµĢ░µĆ¦ŃüīĶ”üµ▒éŃüĢŃéīŃü¬ŃüäÕŹŖńÉåµā│µ░ŚõĮōŃü¦Ńé鵳ÉŃéŖń½ŗŃüżŃĆé ńŖȵģŗµ¢╣ń©ŗÕ╝ÅŃü«ÕŠ«ÕłåŃüŗŃéēÕŠŚŃéēŃéīŃéŗńå▒Ķå©Õ╝Ąõ┐éµĢ░ ╬▒ Ńü©ńŁēµĖ®Õ£¦ńĖ«ńÄć ╬║T Ńü»ŃĆüŃüØŃéīŃü×Ńéī
Ńü¦ŃüéŃéŗŃĆé ńå▒ÕŖøÕŁ”ńÜäńŖȵģŗµ¢╣ń©ŗÕ╝ÅŃüī
Ńü¦ŃüéŃéŖŃĆüÕåģķā©Ńé©ŃāŹŃā½Ńé«Ńā╝ŃéäŃé©Ńā│Ńé┐Ńā½ŃāöŃā╝ŃüīõĮōń®ŹŃéäÕ£¦ÕŖøŃü½õŠØÕŁśŃüŚŃü¬ŃüäµĖ®Õ║”ŃüĀŃüæŃü«ķ¢óµĢ░Ńü©Ńü¬ŃéŗŃĆé ŃéĖŃāźŃā╝Ńā½’╝ØŃāłŃāĀŃéĮŃā│õ┐éµĢ░Ńüī
Ńü¦ŃüéŃéŖŃĆüŃéĖŃāźŃā╝Ńā½’╝ØŃāłŃāĀŃéĮŃā│ÕŖ╣µ×£ŃüīŃü¬ŃüäŃĆé ńŁēÕ£¦ńå▒Õ«╣ķćÅŃü©ńŁēń®Źńå▒Õ«╣ķćÅŃü«ÕĘ«Ńüī
Ńü©Ńü¬ŃéŗŃĆé’╝łŃā×ŃéżŃāżŃā╝Ńü«ķ¢óõ┐éÕ╝Å’╝ē ķ¢óķĆŻķĀģńø« |
Portal di Ensiklopedia Dunia




































