この項目「
自由エネルギー原理 」は翻訳されたばかりのものです。不自然あるいは曖昧な表現などが含まれる可能性があり、このままでは読みづらいかもしれません。(原文:英文記事
Free energy principle (07:18, 9 February 2025) 版)
修正、加筆に協力し、現在の表現をより自然な表現にして下さる方を求めています。
ノートページ や
履歴 も参照してください。
(2025年3月 )
自由エネルギー原理 (じゆうエネルギーげんり、英:Free energy principle)は、脳 の働きに関する理論的枠組み驚き シャノンサプライズ (英語版 ) 脳の目的 は、内部モデルと外界との整合性を高めて予測の正確性を向上させること である。この原理はベイズ推定 能動的推論 (英語版 ) 予測 によって行動 が導かれ、その行動 がもたらす感覚フィードバック によって予測 が精緻化されるとする。この原理は、脳機能 、知覚 行動 [ 1]
生物物理学 および認知科学 において、自由エネルギー原理[ 2] シャノンサプライズ (英語版 ) 驚き の度合い(ある結果の負の対数確率)を最小化すること、言い換えればその変分上界である自由エネルギー 脳機能へのベイズ的取組み (英語版 ) 人工知能 変分ベイズ法 (英語版 ) カール・フリストン (英語版 ) 神経科学 における身体的知覚-行動ループ の説明として導入された。[ 3]
自由エネルギー原理は、あるシステムが他のシステム(例えば、システムが埋め込まれた環境)と分けられてはいるが離れがたく結びついているような場合に、そのシステムの振る舞いをモデル化する。このとき、システムと外界をつなぐ界面を十分に表現できる自由度を持った変数の集合をマルコフ・ブランケット (英語版 ) 内部と外部の状態 、またはシステムの経路 として知られている。
自由エネルギー原理は、脳が推論エンジン であるとするベイズ的な考え方に基づいている。この原理の下では、システムは驚き が最小になる経路を追い求める。表現を変えると、システムは自身の世界モデルに基づく予測 と、感覚 および知覚 差 を最小にしている。この差 は変分自由エネルギー として定量化され、システムの世界モデルの継続的な修正、または世界をシステムの予測 に近づけることで最小化される。つまり、システムが自由エネルギーを最小化するには、世界モデルを変えるのでは無く、世界そのものを能動的に変え、期待される状態に近づけるという方法もあるということである。
フリストンはこのことを、すべての生体反応の原理とみなす。[ 4] [ 4]
自由エネルギー原理は情報物理学の数学的原理であり、最大エントロピー原理や最小作用の原理に似て、数学的な観点から真である。自由エネルギー原理を否定しようとするのはカテゴリー誤認であり、経験的観測により微積分 を否定しようとするのと同類である。(こういうやり方では数学的理論の間違いを示すことはできない;必要なのは理論から形式的矛盾を導くことである。)2018年のインタビューで、フリストンは 自由エネルギー原理が反証 の対象ではないということを以下のように説明した:[ 5]
私はここで基本的な区別をしておくことが有用だと思います。この区別は、言明と過程の理論との違いなのです;つまり、物事が従うかもしれない規範的な原理と、その原理がどのように実現されるかについての過程の理論すなわち仮説との違いなのです。
この区別の下では、自由エネルギー原理は予測符号化 (英語版 ) 原理 最小作用の原理 のように、この原理も反証できず、否定できません。
実際、それに対してできることはあまりなく、測定可能なシステムがこの原理に従うかどうか問う以外にはありません。一方で、脳がベイズ推定や予測符号化のような形で行動するという仮説は、まさに仮説であり、経験的証拠で支持されることもあれば、されないこともあります。
経験的な証拠に支持された、このような仮説の例は多い。[ 6]
細胞や脳のような自己組織化 する生体システムは、変分自由エネルギーを最小化するものとして理解できる という考え方は、ヘルムホルツ の無意識的推論 (英語版 ) [ 7] [ 8] [ 9] 変分 確率密度は、仮定された原因から観測結果を予測して生成する確率モデルに関連して定義される。この文脈において、自由エネルギーは周辺尤度(ベイズ的証拠) (英語版 ) [ 10]
しかしながら、自由エネルギーは結果の自己情報量 驚き [ 訳注 1] [ 11] [ 12]
能動的推論は、良いレギュレーター定理 (英語版 ) [ 13] 自己組織化 に関する報告[ 14] [ 15] 自己集合 、パターン形成 (英語版 ) オートポイエーシス [ 16] プラクトポイエーシス (英語版 ) [ 17] サイバネティックス 、シナジェティクス(物理) (英語版 ) [ 18] 身体化された認知 で検討されたテーマを扱っている。
自由エネルギーは、ある変分確率密度の下で観測が期待されるエネルギーから、そのエントロピーを引いた形で表せるので、最大エントロピー原理 とも関連がある。[ 19] [ 訳注 2] 作用 最小変分自由エネルギー原理 は 結局のところ、最小作用の原理
スケール不変性を可能にする能動的推論は、他の理論や分野にも応用されている。例えば、社会学 [ 20] [ 21] [ 22] [ 23] 言語学 およびコミュニケーション[ 24] [ 25] [ 26] 記号学 [ 27] [ 28] 疫学 [ 29]
また、負の自由エネルギーは、エビデンス下限 (英語版 ) 機械学習 において変分オートエンコーダ などの生成モデル を教育する際に広く使用される。
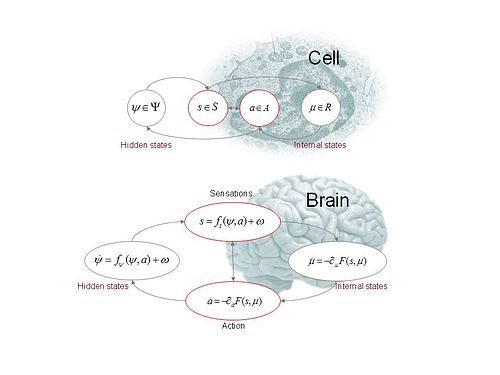
図1: これらの模式図は、状態を内部状態(Internal states)
μ
(
t
)
{\displaystyle \mu (t)}
外部状態(External [Hidden, Latent] states)
ψ
(
t
)
{\displaystyle \psi (t)}
マルコフブランケット によって分離されることを示している。マルコフブランケット は、感覚状態
s
(
t
)
{\displaystyle s(t)}
行動状態
a
(
t
)
{\displaystyle a(t)}
内部状態 が細胞内側の状態に対応し、感覚状態 は細胞膜の表面状態となり、そのすぐ内側に行動状態 (例:細胞骨格のアクチンフィラメント)が存在する形になっている。 下段の図は、この分割が脳における行動 と知覚 に適用される様子を示している。ここでは、行動状態 (Active states, 図中ではAction)と内部状態 (Internal states)が、感覚状態 (sensory states, 図中ではSensation)に関する自由エネルギー汎関数を最小化 する。続いて起こる、内部状態 の自己組織化 が知覚 に対応し、行動 (Action)は脳の状態を外部状態 へと戻す形で結びつける役割を果たす。 能動的推論 は、生成的モデル から得られる感覚 データの原因 を、近似ベイズ推論 (英語版 ) 推論 し、それらの推論の結果を行動 の指針として用いる。
ベイズの定理 は、このような因果モデルの確率論的に最適な反転(結果から原因を推定すること)を定式化するが、その適用は一般に計算的に困難である。そのため、実用的には近似的な手法が用いられることが多い。
能動的推論 においては、こうした近似手法の中でも変分法 が主要な役割を果たす。これは実践的および理論的な理由によるものである。実践的な理由として、変分法はしばしば単純な推論手続きを提供する点が挙げられる。一方、理論的な理由として、この手法が上記で説明したような物理学の基本原理と関連している点がある。
これらの変分法は、ベイズ最適推論(または事後確率 )とその近似との 違い の 上限 を最小化することで進んでいく。この上限は自由エネルギーとして知られている。この概念に基づき、知覚 は、入力される感覚情報 について自由エネルギーを最小化する過程 として特徴づけることができる。一方、行動 は、出力される行動情報 について同じ自由エネルギーを最小化する過程 として捉えることができる。
このような全体として双対な最適化は、能動的推論 の特徴である。そして、自由エネルギー原理は、「知覚 し、行動 するすべてのシステムは、この方法で記述できる」という仮説である。[ 訳注 3]
自由エネルギー原理を通じて能動的推論 の仕組みを具体的に説明するためには、生成モデル を明確に定義する必要がある。この生成モデル は、複数の確率密度関数 を含み、それらが組み合わされて因果モデルを特徴づける。
その一例として次のように定義される。
システムは状態空間
X
{\displaystyle X}
X
=
Ψ
×
S
×
A
×
R
{\displaystyle X=\Psi \times S\times A\times R}
ここで、
Ψ
{\displaystyle \Psi }
外部状態 の空間であり、この状態には直接的な知覚やアクセスができない。
S
{\displaystyle S}
感覚状態 の空間である。
A
{\displaystyle A}
行動 の空間である。
R
{\displaystyle R}
内部状態 の空間であり、外部には公開されない。図1に従い、以後
ψ
˙
,
ψ
,
s
,
a
{\displaystyle {\dot {\psi }},\psi ,s,a}
μ
{\displaystyle \mu }
t
{\displaystyle t}
生成モデル は次に示す確率密度関数によって具体的に定義される。
p
S
:
S
×
Ψ
×
A
→
R
{\displaystyle p_{S}:S\times \Psi \times A\to \mathbb {R} }
p
S
(
s
∣
ψ
,
a
)
{\displaystyle p_{S}(s\mid \psi ,a)}
この関数は、外部状態
ψ
{\displaystyle \psi }
Φíîσïò
a
{\displaystyle a}
s
{\displaystyle s}
尤度 )を特徴づける。
p
Ψ
:
Ψ
×
Ψ
×
A
→
R
{\displaystyle p_{\Psi }:\Psi \times \Psi \times A\to \mathbb {R} }
p
Ψ
(
ψ
˙
∣
ψ
,
a
)
{\displaystyle p_{\Psi }({\dot {\psi }}\mid \psi ,a)}
この関数は、エージェントの行動 a を所与として、外部状態 ψ が時間 t においてどのように変化すると予測されるかを特徴づける。
p
A
:
A
×
R
×
S
→
R
{\displaystyle p_{A}:A\times R\times S\to \mathbb {R} }
p
A
(
a
∣
μ
,
s
)
{\displaystyle p_{A}(a\mid \mu ,s)}
この関数は、エージェントの行動
a
{\displaystyle a}
、内部状態
μ
{\displaystyle \mu }
感覚 データ
s
{\displaystyle s}
p
R
:
R
×
S
→
R
{\displaystyle p_{R}:R\times S\to \mathbb {R} }
p
R
(
μ
∣
s
)
{\displaystyle p_{R}(\mu \mid s)}
この関数は、エージェントの内部状態
μ
{\displaystyle \mu }
感覚 データ
s
{\displaystyle s}
これらの確率密度関数は、「結合モデル」の要素を決定する。この結合モデルは、生成モデル の完全な仕様を表すものであり、次のように記述される: 
p
(
ψ
˙
,
s
,
a
,
μ
∣
ψ
)
=
p
S
(
s
∣
ψ
,
a
)
p
Ψ
(
ψ
˙
∣
ψ
,
a
)
p
A
(
a
∣
μ
,
s
)
p
R
(
μ
∣
s
)
{\displaystyle p({\dot {\psi }},s,a,\mu \mid \psi )=p_{S}(s\mid \psi ,a)p_{\Psi }({\dot {\psi }}\mid \psi ,a)p_{A}(a\mid \mu ,s)p_{R}(\mu \mid s)}
次に、ベイズの定理 に基づき、「事後確率 密度」
p
Bayes
(
ψ
˙
|
s
,
a
,
μ
,
ψ
)
{\displaystyle p_{\text{Bayes}}({\dot {\psi }}|s,a,\mu ,\psi )}
外部状態
ψ
{\displaystyle \psi }
Φíîσïò
a
{\displaystyle a}
感覚 信号
s
{\displaystyle s}
内部状態
μ
{\displaystyle \mu }
外部状態
ψ
˙
{\displaystyle {\dot {\psi }}}
信念 を表す。
しかし、この事後確率密度
p
Bayes
{\displaystyle p_{\text{Bayes}}}
p
Bayes
{\displaystyle p_{\text{Bayes}}}
q
(
ψ
˙
|
s
,
a
,
μ
,
ψ
)
{\displaystyle q({\dot {\psi }}|s,a,\mu ,\psi )}
このとき、自由エネルギー は以下のように定義される。
F
(
μ
,
a
;
s
)
⏟
f
r
e
e
−
e
n
e
r
g
y
=
E
q
(
ψ
˙
)
[
−
log
p
(
ψ
˙
,
s
,
a
,
μ
∣
ψ
)
]
⏟
expected energy
−
H
[
q
(
ψ
˙
∣
s
,
a
,
μ
,
ψ
)
]
⏟
e
n
t
r
o
p
y
=
−
log
p
(
s
)
⏟
s
u
r
p
r
i
s
e
+
K
L
[
q
(
ψ
˙
∣
s
,
a
,
μ
,
ψ
)
∥
p
Bayes
(
ψ
˙
∣
s
,
a
,
μ
,
ψ
)
]
⏟
d
i
v
e
r
g
e
n
c
e
≥
−
log
p
(
s
)
⏟
s
u
r
p
r
i
s
e
{\displaystyle {\begin{aligned}{\underset {\mathrm {free-energy} }{\underbrace {F(\mu ,a\,;s)} }}&={\underset {\text{expected energy}}{\underbrace {\mathbb {E} _{q({\dot {\psi }})}[-\log p({\dot {\psi }},s,a,\mu \mid \psi )]} }}-{\underset {\mathrm {entropy} }{\underbrace {\mathbb {H} [q({\dot {\psi }}\mid s,a,\mu ,\psi )]} }}\\&={\underset {\mathrm {surprise} }{\underbrace {-\log p(s)} }}+{\underset {\mathrm {divergence} }{\underbrace {\mathbb {KL} [q({\dot {\psi }}\mid s,a,\mu ,\psi )\parallel p_{\text{Bayes}}({\dot {\psi }}\mid s,a,\mu ,\psi )]} }}\\&\geq {\underset {\mathrm {surprise} }{\underbrace {-\log p(s)} }}\end{aligned}}}
この式は、
自由エネルギー (free-energy) が、期待エネルギー (expected energy) から エントロピー (entropy) を 引いたものとして表されることを示しており、また、自由エネルギーを
驚き(surprise) : 
−
log
p
(
s
)
{\displaystyle -\log p(s)}
s
{\displaystyle s}
カルバック・ライブラー(KL)発散
K
L
[
q
∥
p
Bayes
]
{\displaystyle \mathbb {KL} [q\parallel p_{\text{Bayes}}]}
q
{\displaystyle q}
p
Bayes
{\displaystyle p_{\text{Bayes}}}
の和として表わすこともできることを示している。 
そして、行動 と知覚 は、次のような同時最適化問題として定義される。
μ
∗
=
a
r
g
m
i
n
μ
{
F
(
μ
,
a
;
s
)
)
}
a
∗
=
a
r
g
m
i
n
a
{
F
(
μ
∗
,
a
;
s
)
}
{\displaystyle {\begin{aligned}\mu ^{*}&={\underset {\mu }{\operatorname {arg\,min} }}\{F(\mu ,a\,;\,s))\}\\a^{*}&={\underset {a}{\operatorname {arg\,min} }}\{F(\mu ^{*},a\,;\,s)\}\end{aligned}}}
内部状態
μ
{\displaystyle \mu }
μ
∗
{\displaystyle \mu ^{*}}
F
{\displaystyle F}
μ
{\displaystyle \mu }
Φíîσïò
a
{\displaystyle a}
a
∗
{\displaystyle a^{*}}
内部状態
μ
∗
{\displaystyle \mu ^{*}}
F
{\displaystyle F}
a
{\displaystyle a}
ここで、内部状態
μ
{\displaystyle \mu }
q
{\displaystyle q}
内部状態は 、外部状態
Ψ
{\displaystyle \Psi }
事後信念 に関するエージェントの最良の推測 を表すものとみなされる。
自由エネルギーは、エージェントの(ぎりぎり または 平均的な)感覚的驚き の上限でもあることに注意する。したがって、自由エネルギーの最小化は、驚き の最小化という観点からも動機づけられる。
自己組織化システムがランダム力学システム (英語版 ) [ 30] 行動 と感覚状態 を含むマルコフ・ブランケット (英語版 ) 内部状態 と外部状態 を分離する役割を果たすものである。 もし内部状態 と行動 が自由エネルギーを最小化するならば、それは感覚状態のエントロピーの上限を設定することになる:
lim
T
→
∞
1
T
∫
0
T
F
(
s
(
t
)
,
μ
(
t
)
)
d
t
⏟
free-action
≥
lim
T
→
∞
1
T
∫
0
T
−
log
p
(
s
(
t
)
∣
m
)
⏟
surprise
d
t
=
H
[
p
(
s
∣
m
)
]
{\displaystyle \lim _{T\to \infty }{\frac {1}{T}}{\underset {\text{free-action}}{\underbrace {\int _{0}^{T}F(s(t),\mu (t))\,dt} }}\geq \lim _{T\to \infty }{\frac {1}{T}}\int _{0}^{T}{\underset {\text{surprise}}{\underbrace {-\log p(s(t)\mid m)} }}\,dt=H[p(s\mid m)]}
これは、エルゴード性 の仮定のもとでは、長期的な驚き の平均がエントロピーと等しくなるためである。この上限は、(熱力学第二法則 や ゆらぎの定理 に関連付けられた)無秩序への自然な傾向に対抗する。
 しかしながら、生命科学における統一原理を、ランダム力学系、非平衡定常状態、およびエルゴード性といった統計物理学の概念に基づいて定式化することは、生物システムを理論的・実証的に研究する上で重大な制約を課すことになる。その結果、生物システムを単なる自己組織化システムの中でも興味深いものとしている特性が、見えにくくなるというリスクが伴う。[ 31]
すべてのベイズ推論は、自由エネルギーの最小化という観点から記述できる。[ 32] [出典無効 自由エネルギーが内部状態について最小化されるとき、隠れ状態 (外部状態)上で、変分確率密度と事後確率密度の間のカルバック・ライブラー(KL)発散 が 最小化される。これは、変分確率密度の式が固定されている場合には近似的なベイズ推論 となり、そうでない場合には厳密なベイズ推論 となる。
したがって、自由エネルギーの最小化は、ベイズ推論やフィルタリング(例:カルマンフィルター )を包括的に記述する方法を提供する。また、自由エネルギーの最小化は、ベイズモデル選択 (英語版 ) 複雑さ (complexity) と 正確さ (accuracy) の差に分解できる:
F
(
s
,
μ
)
⏟
free-energy
=
D
K
L
[
q
(
ψ
∣
μ
)
∥
p
(
ψ
∣
m
)
]
⏟
complexity
−
E
q
[
log
p
(
s
∣
ψ
,
m
)
]
⏟
a
c
c
u
r
a
c
y
{\displaystyle {\underset {\text{free-energy}}{\underbrace {F(s,\mu )} }}={\underset {\text{complexity}}{\underbrace {D_{\mathrm {KL} }[q(\psi \mid \mu )\parallel p(\psi \mid m)]} }}-{\underset {\mathrm {accuracy} }{\underbrace {E_{q}[\log p(s\mid \psi ,m)]} }}}
最小自由エネルギーを持つモデルは、(複雑さ のコスト(例:オッカムの剃刀 や、より形式的な計算コストの取り扱い[ 33] 複雑さ とは、ある隠れ状態 の下で 変分確率密度 と 事前信念 の間の相違である。すなわちこれは、データを説明するために使用される有効自由度 である[ 訳注 4]
変分自由エネルギーは、情報理論的な関数であり、熱力学的な(ヘルムホルツ )自由エネルギー とは異なる[ 34] 複雑さ 項は、ヘルムホルツ自由エネルギーと同じ不動点を持つ(ただし、システムが熱力学的に閉じているが孤立していないと仮定した場合である)。その理由は、感覚的な外乱が(十分に長い時間にわたって)止められると、複雑さ が最小化されるためである(なぜなら、正確さ が無視できるからである[ 訳注 5] 最小エネルギー原理 (英語版 ) [ 35]
自由エネルギーの最小化は、感覚状態 と、(エントロピーが固定されている場合の)変分確率分布のパラメーターとしての内部状態 との間の、相互情報量 [ 36] [ 12]
自由エネルギーの最小化は、不確実性のもとで神経が推論 や学習 を行うことを、標準(ベイズ最適)モデルとして定式化するための有用な方法である[ 37] ベイズ脳仮説 (英語版 ) [ 38] [ 訳注 6] 隠れ状態 の性質に依存する:
Ψ
=
X
×
Θ
×
Π
{\displaystyle \Psi =X\times \Theta \times \Pi }
これは、時間に依存する変数 と、時間不変なパラメーター と、確率的変動の精度 (すなわち逆分散または温度)から成る。変数での最小化 、パラメーターでの最小化 、および 精度での最小化 は、それぞれ 推論 、学習 、不確実性の符号化 に対応する。
自由エネルギーの最小化は、知覚における 無意識の推論 (英語版 ) [ 7] [ 9]
ニューロンの動態(neuronal dynamics)の関連過程理論(associated process theory)は、自由エネルギーを勾配降下法 によって最小化することに基づいている。これは、一般化ベイズ・フィルタリング (英語版 ) 一般化運動座標 の変数を、
D
{\displaystyle D}
[ 39]
μ
~
˙
=
D
μ
~
−
∂
μ
F
(
s
,
μ
)
|
μ
=
μ
~
{\displaystyle {\dot {\tilde {\mu }}}=D{\tilde {\mu }}-\partial _{\mu }F(s,\mu ){\Big |}_{\mu ={\tilde {\mu }}}}
通常、自由エネルギーを定義する 生成モデル は、非線形 かつ (脳の皮質の階層 と似て)階層的 である。
一般化フィルタリング の特別なケースには、カルマンフィルター が含まれる。これは、予測符号化 (英語版 ) [ 40]
階層モデルのもとで、予測符号化には 上向き(ボトムアップ)の予測誤差 および 下向き(トップダウン)の予測の回帰的な交換が 伴う[ 41] 感覚系 [ 42] 運動器系 [ 43]
予測符号化 において、自由エネルギー(自由行動[ 訳注 7] ヘッブ的可塑性 (Hebbian plasticity)に帰着し、脳におけるシナプス可塑性 (synaptic plasticity) と関連している。
精度パラメーター(precision parameters)の最適化は、予測誤差 のゲインの最適化に対応する(例えば、カルマンゲイン )。神経生理学的に妥当な予測符号化の実装[ 41] 錐体細胞 (superficial pyramidal cells)の興奮性(英語版) の最適化に対応し、注意 [ 44]
複数の対象物が存在する環境において、SAIM(Selective Attention in Intelligence Model)のベイズ的再構成版である PE-SAIM によって実行された選択的注意 課題の結果をシミュレーションした。 このグラフは、 FOA(Focus of Attention、注意 の焦点)および2つのテンプレートユニットが、知識ネットワーク内で活性化する時間的推移 を示している。 注意 に関するトップダウン vs. ボトムアップ論争は、主要な未解決問題として取り上げられてきた。この課題に対し、ある計算モデルが、トップダウンとボトムアップのメカニズムが相互作用する 循環的な性質 を示すことに成功した。注意 の創発モデル(emergent model of attention)として確立された SAIM というモデルを用いて、著者らはPE-SAIM というモデルを提案した。これは標準版とは対照的に、選択的注意 にトップダウン的な視点からアプローチする。このモデルは、予測誤差 を同じレベルまたは上位レベルへ伝達することを考慮に入れている。これは、データ と その原因(または、生成モデル と 事後確率 )との間の差を示すエネルギー関数を最小化するためである。モデルの妥当性を高めるために、著者らは刺激間の神経競合(neural competition)も組み込んだ。このモデルの顕著な特徴は、課題実行中において、自由エネルギー関数を予測誤差のみを用いて再定式化した点である。:
∂
E
t
o
t
a
l
(
Y
V
P
,
X
S
N
,
x
C
N
,
y
K
N
)
∂
y
m
n
S
N
=
x
m
n
C
N
−
b
C
N
ε
n
m
C
N
+
b
C
N
∑
k
(
ε
k
n
m
K
N
)
{\displaystyle {\dfrac {\partial E^{total}(Y^{VP},X^{SN},x^{CN},y^{KN})}{\partial y_{mn}^{SN}}}=x_{mn}^{CN}-b^{CN}\varepsilon _{nm}^{CN}+b^{CN}\sum _{k}(\varepsilon _{knm}^{KN})}
ここで、
E
t
o
t
a
l
{\displaystyle E^{total}}
ε
k
n
m
K
N
{\displaystyle \varepsilon _{knm}^{KN}}
事前確率 )と事後確率 との間の予測誤差 であり、時間とともに変化する[ 45] 注意 (covert selective visual attention)」におけるテンプレートマッチング(template matching)の計算モデルを提案した[ 46]
この研究によれば、全状態空間の総自由エネルギー は、元の神経ネットワークにトップダウン信号を挿入することで達せられる[ 訳注 8] フィードフォワード (英語版 ) フィードバック の両方の予測誤差を含む動的システムが導き出される。
勾配降下法 が行動
a
˙
=
−
∂
a
F
(
s
,
μ
~
)
{\displaystyle {\dot {a}}=-\partial _{a}F(s,{\tilde {\mu }})}
皮質脊髄 性)の予測によって活性化される 古典的な反射弓 の観点から理解することができる。 この枠組みは、平衡点 解の自由度 問題への一般化[ 47] 運動軌道 への一般化 のための形式を提供する。
能動的推論 は、最適制御 最適制御 の価値関数 やコスト関数 を、状態遷移 流れ 事前信念 に置き換えることで得られる[ 48] ベルマン方程式 の解 との密接な関係を活用して行われる。 しかし、能動的推論 は、以下の 流れ についての事前確率分布から始まる:
f
=
Γ
⋅
∇
V
+
∇
×
W
{\displaystyle f=\Gamma \cdot \nabla V+\nabla \times W}
 これは、状態空間におけるスカラー関数
V
(
x
)
{\displaystyle V(x)}
W
(
x
)
{\displaystyle W(x)}
ヘルムホルツ分解  を参照のこと)。
 ここで、
Γ
{\displaystyle \Gamma }
c
(
x
)
=
f
⋅
∇
V
+
∇
⋅
Γ
⋅
V
{\displaystyle c(x)=f\cdot \nabla V+\nabla \cdot \Gamma \cdot V}
流れ についての事前確率分布
p
(
x
~
∣
m
)
{\displaystyle p({\tilde {x}}\mid m)}
p
(
x
∣
m
)
=
exp
(
V
(
x
)
)
{\displaystyle p(x\mid m)=\exp(V(x))}
 これは、適切な順方向コルモゴロフ方程式 (英語版 ) [ 49]
対照的に、最適制御 はコスト関数を所与とし、以下の仮定のもとで流れを最適化する:
W
=
0
{\displaystyle W=0}
流れ は 渦なし場 (英語版 ) 詳細釣り合い を満たす事を示している)。通常、この方法では逆方向コルモゴロフ方程式 を解く必要がある[ 50]
最適決定 (英語版 ) 部分観測マルコフ決定過程 として定式化される)は、能動的推論 の枠組みにおいて、効用関数 事前信念 に組み込むことで処理される。 この設定において、エージェントが期待するのは、高い効用(低いコスト)を持つ状態を占めること である。 生成モデル に、制御をモデル化する隠れ状態 を組み込むことで、変分自由エネルギーを最小化する方策(制御系列)は、高い効用を持つ状態に至る[ 51]
神経科学 的に、ドーパミン などの神経調節 (英語版 ) [ 52] [ 53] [ 54]
能動的推論は、認知神経科学 、脳機能、および神経精神医学 におけるさまざまな問題に対処するために使用されてきた。これには、以下が含まれる:行動観察[ 55] ミラーニューロン [ 56] サッカード (英語版 ) 視覚探索 [ 57] [ 58] 眼球運動 [ 59] 睡眠 [ 60] 錯覚 [ 61] 注意 [ 44] 行動選択 (英語版 ) [ 52] 意識 [ 62] [ 63] ヒステリー [ 64] 精神病 [ 65] [ 66]
References
^ Bruineberg, Jelle; Kiverstein, Julian; Rietveld, Erik (2018). “The anticipating brain is not a scientist: the free-energy principle from an ecological-enactive perspective” . Synthese 195 (6): 2417–2444. doi :10.1007/s11229-016-1239-1 . PMC 6438652 . PMID 30996493 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6438652/ . ^ Friston, Karl (2010). “The free-energy principle: a unified brain theory?” . Nature Reviews Neuroscience 11 (2): 127–138. doi :10.1038/nrn2787 . PMID 20068583 . https://www.nature.com/articles/nrn2787 2023年7月9日閲覧。 . ^ Friston, Karl; Kilner, James; Harrison, Lee (2006). “A free energy principle for the brain” . Journal of Physiology-Paris 100 (1–3): 70–87. doi :10.1016/j.jphysparis.2006.10.001 . PMID 17097864 . http://www.fil.ion.ucl.ac.uk/~karl/A%20free%20energy%20principle%20for%20the%20brain.pdf . ^ a b Shaun Raviv: The Genius Neuroscientist Who Might Hold the Key to True AI . In: Wired, 13. November 2018
^ Friston, Karl (2018). ΓÇ£Of woodlice and men: A Bayesian account of cognition, life and consciousness. An interview with Karl Friston (by Martin Fortier & Daniel Friedman)ΓÇ¥ . ALIUS Bulletin 2 : 17ΓÇô43. https://www.aliusresearch.org/bulletin02.html . ^ Friston, Karl (2022). Active Inference: The Free Energy Principle in Mind, Brain, and Behavior ISBN 9780262045353 . https://books.google.com/books?id=KXZ_zgEACAAJ&q=Table+9.1 ^ a b Helmholtz, H. (1866/1962). Concerning the perceptions in general. In Treatise on physiological optics (J. Southall, Trans., 3rd ed., Vol. III). New York: Dover. Available at https://web.archive.org/web/20180320133752/http://poseidon.sunyopt.edu/BackusLab/Helmholtz/
^ Gregory, R. L. (1980-07-08). ΓÇ£Perceptions as hypothesesΓÇ¥. Philosophical Transactions of the Royal Society of London. B, Biological Sciences 290 (1038): 181ΓÇô197. Bibcode : 1980RSPTB.290..181G . doi :10.1098/rstb.1980.0090 . JSTOR 2395424 . PMID 6106237 . ^ a b Dayan, Peter; Hinton, Geoffrey E.; Neal, Radford M.; Zemel, Richard S. (1995). ΓÇ£The Helmholtz MachineΓÇ¥ . Neural Computation 7 (5): 889ΓÇô904. doi :10.1162/neco.1995.7.5.889 . hdl :21.11116/0000-0002-D6D3-E PMID 7584891 . http://www.gatsby.ucl.ac.uk/~dayan/papers/hm95.pdf .
^ Beal, M. J. (2003). Variational Algorithms for Approximate Bayesian Inference . Ph.D. Thesis, University College London.
^ Sakthivadivel, Dalton (2022). ΓÇ£Towards a Geometry and Analysis for Bayesian MechanicsΓÇ¥. arXiv :2204.11900 math-ph ]. ^ a b Ramstead, Maxwell; Sakthivadivel, Dalton; Heins, Conor; Koudahl, Magnus; Millidge, Beren; Da Costa, Lancelot; Klein, Brennan; Friston, Karl (2023). ΓÇ£On Bayesian mechanics: A physics of and by beliefsΓÇ¥ . Interface Focus 13 (3). arXiv :2205.11543 . doi :10.1098/rsfs.2022.0029 . PMC 10198254 . PMID 37213925 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC10198254/ .
^ Conant, Roger C.; Ross Ashby, W. (1970). ΓÇ£Every good regulator of a system must be a model of that systemΓÇ¥. International Journal of Systems Science 1 (2): 89ΓÇô97. doi :10.1080/00207727008920220 . ^ Kauffman, S. (1993). The Origins of Order: Self-Organization and Selection in Evolution . Oxford: Oxford University Press.
^ Nicolis, G., & Prigogine, I. (1977). Self-organization in non-equilibrium systems. New York: John Wiley.
^ Maturana, H. R., & Varela, F. (1980). Autopoiesis: the organization of the living . In V. F. Maturana HR (Ed.), Autopoiesis and Cognition. Dordrecht, Netherlands: Reidel.
^ Nikoli─ç, Danko (2015). ΓÇ£Practopoiesis: Or how life fosters a mindΓÇ¥. Journal of Theoretical Biology 373 : 40ΓÇô61. arXiv :1402.5332 . Bibcode : 2015JThBi.373...40N . doi :10.1016/j.jtbi.2015.03.003 . PMID 25791287 . ^ Haken, H. (1983). Synergetics: An introduction. Non-equilibrium phase transition and self-organisation in physics, chemistry and biology (3rd ed.). Berlin: Springer Verlag.
^ Jaynes, E. T. (1957). “Information Theory and Statistical Mechanics” . Physical Review 106 (4): 620–630. Bibcode : 1957PhRv..106..620J . doi :10.1103/PhysRev.106.620 . http://bayes.wustl.edu/etj/articles/theory.1.pdf . ^ Veissière, Samuel P. L.; Constant, Axel; Ramstead, Maxwell J. D.; Friston, Karl J.; Kirmayer, Laurence J. (2020). “Thinking through other minds: A variational approach to cognition and culture” (英語). Behavioral and Brain Sciences 43 : e90. doi :10.1017/S0140525X19001213 . ISSN 0140-525X . PMID 31142395 . https://www.cambridge.org/core/journals/behavioral-and-brain-sciences/article/abs/thinking-through-other-minds-a-variational-approach-to-cognition-and-culture/9A10399BA85F428D5943DD847092C14A . ^ Ramstead, Maxwell J. D.; Constant, Axel; Badcock, Paul B.; Friston, Karl J. (2019-12-01). “Variational ecology and the physics of sentient systems” (英語). Physics of Life Reviews . Physics of Mind 31 : 188–205. Bibcode : 2019PhLRv..31..188R . doi :10.1016/j.plrev.2018.12.002 . ISSN 1571-0645 . PMC 6941227 . PMID 30655223 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6941227/ . ^ Albarracin, Mahault; Demekas, Daphne; Ramstead, Maxwell J. D.; Heins, Conor (April 2022). “Epistemic Communities under Active Inference” (英語). Entropy 24 (4): 476. Bibcode : 2022Entrp..24..476A . doi :10.3390/e24040476 . ISSN 1099-4300 . PMC 9027706 . PMID 35455140 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC9027706/ . ^ Albarracin, Mahault; Constant, Axel; Friston, Karl J.; Ramstead, Maxwell James D. (2021). “A Variational Approach to Scripts” . Frontiers in Psychology 12 : 585493. doi :10.3389/fpsyg.2021.585493 . ISSN 1664-1078 . PMC 8329037 . PMID 34354621 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC8329037/ . ^ Friston, Karl J.; Parr, Thomas; Yufik, Yan; Sajid, Noor; Price, Catherine J.; Holmes, Emma (2020-11-01). “Generative models, linguistic communication and active inference” (英語). Neuroscience & Biobehavioral Reviews 118 : 42–64. doi :10.1016/j.neubiorev.2020.07.005 . ISSN 0149-7634 . PMC 7758713 . PMID 32687883 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7758713/ . ^ Tison, Remi; Poirier, Pierre (2021-10-02). “Communication as Socially Extended Active Inference: An Ecological Approach to Communicative Behavior” . Ecological Psychology 33 (3–4): 197–235. doi :10.1080/10407413.2021.1965480 . ISSN 1040-7413 . https://doi.org/10.1080/10407413.2021.1965480 . ^ Friston, Karl J.; Frith, Christopher D. (2015-07-01). “Active inference, communication and hermeneutics” (英語). Cortex . Special issue: Prediction in speech and language processing 68 : 129–143. doi :10.1016/j.cortex.2015.03.025 . ISSN 0010-9452 . PMC 4502445 . PMID 25957007 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4502445/ . ^ Kerusauskaite, Skaiste (2023-06-01). “Role of Culture in Meaning Making: Bridging Semiotic Cultural Psychology and Active Inference” (英語). Integrative Psychological and Behavioral Science 57 (2): 432–443. doi :10.1007/s12124-022-09744-x . ISSN 1936-3567 . PMID 36585542 . https://doi.org/10.1007/s12124-022-09744-x . ^ García, Adolfo M.; Ibáñez, Agustín (2022-11-14) (英語). The Routledge Handbook of Semiosis and the Brain ISBN 978-1-000-72877-4 . https://books.google.com/books?id=hPCKEAAAQBAJ&dq=active+inference+semiotics&pg=PT90 ^ Bottemanne, Hugo; Friston, Karl J. (2021-12-01). “An active inference account of protective behaviours during the COVID-19 pandemic” (英語). Cognitive, Affective, & Behavioral Neuroscience 21 (6): 1117–1129. doi :10.3758/s13415-021-00947-0 . ISSN 1531-135X . PMC 8518276 . PMID 34652601 . https://doi.org/10.3758/s13415-021-00947-0 . ^ Crauel, Hans; Flandoli, Franco (1994). “Attractors for random dynamical systems” . Probability Theory and Related Fields 100 (3): 365–393. doi :10.1007/BF01193705 . https://www.researchgate.net/publication/227072665 . ^ Colombo, Matteo; Palacios, Patricia (2021). “Non-equilibrium thermodynamics and the free energy principle in biology”. Biology & Philosophy 36 (5). doi :10.1007/s10539-021-09818-x . ^ Roweis, Sam; Ghahramani, Zoubin (1999). “A Unifying Review of Linear Gaussian Models” . Neural Computation 11 (2): 305–345. doi :10.1162/089976699300016674 . PMID 9950734 . http://authors.library.caltech.edu/13697/1/ROWnc99.pdf . ^ Ortega, Pedro A.; Braun, Daniel A. (2013). “Thermodynamics as a theory of decision-making with information-processing costs” . Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 469 (2153). arXiv :1204.6481 . Bibcode : 2013RSPSA.46920683O . doi :10.1098/rspa.2012.0683 . http://rspa.royalsocietypublishing.org/content/469/2153/20120683 . ^ Evans, Denis J. (2003). “A non-equilibrium free energy theorem for deterministic systems” . Molecular Physics 101 (10): 1551–1554. Bibcode : 2003MolPh.101.1551E . doi :10.1080/0026897031000085173 . http://rscweb.anu.edu.au/~evans/papers/NEFET.pdf . ^ Jarzynski, C. (1997). “Nonequilibrium Equality for Free Energy Differences”. Physical Review Letters 78 (14): 2690–2693. arXiv :cond-mat/9610209 . Bibcode : 1997PhRvL..78.2690J . doi :10.1103/PhysRevLett.78.2690 . ^ Sakthivadivel, Dalton (2022). “Towards a Geometry and Analysis for Bayesian Mechanics”. arXiv :2204.11900 math-ph ]. ^ Friston, Karl (2010). “The free-energy principle: A unified brain theory?” . Nature Reviews Neuroscience 11 (2): 127–138. doi :10.1038/nrn2787 . PMID 20068583 . http://www.fil.ion.ucl.ac.uk/~karl/The%20free-energy%20principle%20A%20unified%20brain%20theory.pdf . ^ Knill, David C.; Pouget, Alexandre (2004). “The Bayesian brain: The role of uncertainty in neural coding and computation” . Trends in Neurosciences 27 (12): 712–719. doi :10.1016/j.tins.2004.10.007 . PMID 15541511 . オリジナル の2016-03-04時点におけるアーカイブ。. https://web.archive.org/web/20160304044221/http://mrl.isr.uc.pt/pub/bscw.cgi/d27540/ReviewKnillPouget2.pdf 2013年5月31日閲覧。 . ^ Friston, Karl; Stephan, Klaas; Li, Baojuan; Daunizeau, Jean (2010). “Generalised Filtering”. Mathematical Problems in Engineering 2010 : 1–34. doi :10.1155/2010/621670 . ^ Knill, David C.; Pouget, Alexandre (2004). “The Bayesian brain: The role of uncertainty in neural coding and computation” . Trends in Neurosciences 27 (12): 712–719. doi :10.1016/j.tins.2004.10.007 . PMID 15541511 . https://www.cs.utexas.edu/users/dana/nn.pdf . ^ a b Mumford, D. (1992). “On the computational architecture of the neocortex” . Biological Cybernetics 66 (3): 241–251. doi :10.1007/BF00198477 . PMID 1540675 . http://cs.brown.edu/people/tld/projects/cortex/course/suggested_reading_list/supplements/documents/MumfordBC-92.pdf .
^ Bastos, Andre M.; Usrey, W. Martin; Adams, Rick A.; Mangun, George R.; Fries, Pascal; Friston, Karl J. (2012). ΓÇ£Canonical Microcircuits for Predictive CodingΓÇ¥ . Neuron 76 (4): 695ΓÇô711. doi :10.1016/j.neuron.2012.10.038 . PMC 3777738 . PMID 23177956 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3777738/ . ^ Adams, Rick A.; Shipp, Stewart; Friston, Karl J. (2013). ΓÇ£Predictions not commands: Active inference in the motor systemΓÇ¥ . Brain Structure and Function 218 (3): 611ΓÇô643. doi :10.1007/s00429-012-0475-5 . PMC 3637647 . PMID 23129312 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3637647/ . ^ a b Friston, Karl J.; Feldman, Harriet (2010). ΓÇ£Attention, Uncertainty, and Free-EnergyΓÇ¥ . Frontiers in Human Neuroscience 4 : 215. doi :10.3389/fnhum.2010.00215 . PMC 3001758 . PMID 21160551 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3001758/ .
^ Abadi, Alireza Khatoon; Yahya, Keyvan; Amini, Massoud; Friston, Karl; Heinke, Dietmar (2019). “Excitatory versus inhibitory feedback in Bayesian formulations of scene construction” . Journal of the Royal Society Interface 16 (154). doi :10.1098/rsif.2018.0344 . PMC 6544897 . PMID 31039693 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6544897/ . ^ “12th Biannual Conference of the German Cognitive Science Society (KogWis 2014)”. Cognitive Processing 15 : 107. (2014). doi :10.1007/s10339-013-0597-6 . ^ Feldman, Anatol G.; Levin, Mindy F. (1995). “The origin and use of positional frames of reference in motor control” . Behavioral and Brain Sciences 18 (4): 723–744. doi :10.1017/S0140525X0004070X . オリジナル の2014-03-29時点におけるアーカイブ。. https://web.archive.org/web/20140329220749/http://e.guigon.free.fr/rsc/article/FeldmanLevin95.pdf 2013年5月31日閲覧。 . ^ Friston, Karl (2011). “What is Optimal about Motor Control?” . Neuron 72 (3): 488–498. doi :10.1016/j.neuron.2011.10.018 . PMID 22078508 . http://www.fil.ion.ucl.ac.uk/~karl/What%20Is%20Optimal%20about%20Motor%20Control.pdf . ^ Friston, Karl; Ao, Ping (2012). “Free Energy, Value, and Attractors” . Computational and Mathematical Methods in Medicine 2012 : 1–27. doi :10.1155/2012/937860 . PMC 3249597 . PMID 22229042 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3249597/ . ^ Kappen, H. J. (2005). “Path integrals and symmetry breaking for optimal control theory”. Journal of Statistical Mechanics: Theory and Experiment 2005 (11): P11011. arXiv :physics/0505066 . Bibcode : 2005JSMTE..11..011K . doi :10.1088/1742-5468/2005/11/P11011 . ^ Friston, Karl; Samothrakis, Spyridon; Montague, Read (2012). “Active inference and agency: Optimal control without cost functions”. Biological Cybernetics 106 (8–9): 523–541. doi :10.1007/s00422-012-0512-8 . hdl :10919/78836 PMID 22864468 . ^ a b Friston, Karl J.; Shiner, Tamara; Fitzgerald, Thomas; Galea, Joseph M.; Adams, Rick; Brown, Harriet; Dolan, Raymond J.; Moran, Rosalyn et al. (2012). “Dopamine, Affordance and Active Inference” . PLOS Computational Biology 8 (1): e1002327. Bibcode : 2012PLSCB...8E2327F . doi :10.1371/journal.pcbi.1002327 . PMC 3252266 . PMID 22241972 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3252266/ .
^ Fiorillo, Christopher D.; Tobler, Philippe N.; Schultz, Wolfram (2003). “Discrete Coding of Reward Probability and Uncertainty by Dopamine Neurons” . Science 299 (5614): 1898–1902. Bibcode : 2003Sci...299.1898F . doi :10.1126/science.1077349 . PMID 12649484 . オリジナル の2016-03-04時点におけるアーカイブ。. https://web.archive.org/web/20160304045504/http://e.guigon.free.fr/rsc/article/FiorilloEtAl03.pdf 2013年5月31日閲覧。 . ^ Frank, Michael J. (2005). “Dynamic Dopamine Modulation in the Basal Ganglia: A Neurocomputational Account of Cognitive Deficits in Medicated and Nonmedicated Parkinsonism” . Journal of Cognitive Neuroscience 17 (1): 51–72. doi :10.1162/0898929052880093 . PMID 15701239 . http://ski.cog.brown.edu/papers/Frank_JOCN.pdf . ^ Friston, Karl; Mattout, Jérémie; Kilner, James (2011). “Action understanding and active inference” . Biological Cybernetics 104 (1–2): 137–160. doi :10.1007/s00422-011-0424-z . PMC 3491875 . PMID 21327826 . http://www.fil.ion.ucl.ac.uk/~karl/Action%20understanding%20and%20active%20inference.pdf . ^ Kilner, James M.; Friston, Karl J.; Frith, Chris D. (2007). “Predictive coding: An account of the mirror neuron system” . Cognitive Processing 8 (3): 159–166. doi :10.1007/s10339-007-0170-2 . PMC 2649419 . PMID 17429704 . http://www.fil.ion.ucl.ac.uk/~karl/Predictive%20coding%20an%20account%20of%20the%20mirror%20neuron%20system.pdf . ^ Friston, Karl; Adams, Rick A.; Perrinet, Laurent; Breakspear, Michael (2012). “Perceptions as Hypotheses: Saccades as Experiments” . Frontiers in Psychology 3 : 151. doi :10.3389/fpsyg.2012.00151 . PMC 3361132 . PMID 22654776 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3361132/ . ^ Mirza, M. Berk; Adams, Rick A.; Mathys, Christoph; Friston, Karl J. (2018). “Human visual exploration reduces uncertainty about the sensed world” . PLOS ONE 13 (1): e0190429. Bibcode : 2018PLoSO..1390429M . doi :10.1371/journal.pone.0190429 . PMC 5755757 . PMID 29304087 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5755757/ . ^ Perrinet, Laurent U.; Adams, Rick A.; Friston, Karl J. (2014). “Active inference, eye movements and oculomotor delays” . Biological Cybernetics 108 (6): 777–801. doi :10.1007/s00422-014-0620-8 . PMC 4250571 . PMID 25128318 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4250571/ . ^ Hobson, J.A.; Friston, K.J. (2012). “Waking and dreaming consciousness: Neurobiological and functional considerations” . Progress in Neurobiology 98 (1): 82–98. doi :10.1016/j.pneurobio.2012.05.003 . PMC 3389346 . PMID 22609044 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3389346/ . ^ Brown, Harriet; Friston, Karl J. (2012). “Free-Energy and Illusions: The Cornsweet Effect” . Frontiers in Psychology 3 : 43. doi :10.3389/fpsyg.2012.00043 . PMC 3289982 . PMID 22393327 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3289982/ . ^ Rudrauf, David; Bennequin, Daniel; Granic, Isabela; Landini, Gregory; Friston, Karl; Williford, Kenneth (2017-09-07). “A mathematical model of embodied consciousness” . Journal of Theoretical Biology 428 : 106–131. Bibcode : 2017JThBi.428..106R . doi :10.1016/j.jtbi.2017.05.032 . PMID 28554611 . http://discovery.ucl.ac.uk/10057795/1/DR_et_al_A_math_model_of_embodied_consciousness_JTBiol_final_revision_for_submission.pdf . ^ K, Williford; D, Bennequin; K, Friston; D, Rudrauf (2018-12-17). “The Projective Consciousness Model and Phenomenal Selfhood” (英語). Frontiers in Psychology 9 : 2571. doi :10.3389/fpsyg.2018.02571 . PMC 6304424 . PMID 30618988 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6304424/ . ^ Edwards, M. J.; Adams, R. A.; Brown, H.; Parees, I.; Friston, K. J. (2012). “A Bayesian account of 'hysteria'” . Brain 135 (11): 3495–3512. doi :10.1093/brain/aws129 . PMC 3501967 . PMID 22641838 . http://www.fil.ion.ucl.ac.uk/~karl/A%20Bayesian%20account%20of%20hysteria.pdf . ^ Adams, Rick A.; Perrinet, Laurent U.; Friston, Karl (2012). “Smooth Pursuit and Visual Occlusion: Active Inference and Oculomotor Control in Schizophrenia” . PLOS ONE 7 (10): e47502. Bibcode : 2012PLoSO...747502A . doi :10.1371/journal.pone.0047502 . PMC 3482214 . PMID 23110076 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3482214/ . ^ Yon, Daniel; Lange, Floris P. de; Press, Clare (2019-01-01). “The Predictive Brain as a Stubborn Scientist” (英語). Trends in Cognitive Sciences 23 (1): 6–8. doi :10.1016/j.tics.2018.10.003 . PMID 30429054 . https://www.cell.com/trends/cognitive-sciences/abstract/S1364-6613(18)30239-0 .
^ 英文Wikipediaでは、自己情報量(self-information)と驚き(surprisal, 情報科学上のsurprise)は、同じ記事にリンクしている。
^ 時間積分の誤りか?
^ 概要の節で、自由エネルギー原理は原理であって仮説ではない と述べているので、矛盾があります。どちらをとるのが正しいか不明なので、原文通りに訳しておきます。今後の編集により矛盾が解消することを期待します。
^ 意味不明。以下の訳。 Here, complexity is the divergence between the variational density and prior beliefs about hidden states (i.e., the effective degrees of freedom used to explain the data).
^ 意味不明。原文は (because accuracy can be neglected)
^ 原文の "neuronal process": 神経(ニューロンの)突起 を、 "neural process": 神経の過程 の誤りとみて訳しました。
^ この文脈での意味不明。
^ 意味不明。「全状態空間の総自由エネルギーの最小値 に達する」ということか? 原文は以下 According to this study, the total free energy of the whole state-space is reached by inserting top-down signals in the original neural networks,






























![{\displaystyle {\begin{aligned}{\underset {\mathrm {free-energy} }{\underbrace {F(\mu ,a\,;s)} }}&={\underset {\text{expected energy}}{\underbrace {\mathbb {E} _{q({\dot {\psi }})}[-\log p({\dot {\psi }},s,a,\mu \mid \psi )]} }}-{\underset {\mathrm {entropy} }{\underbrace {\mathbb {H} [q({\dot {\psi }}\mid s,a,\mu ,\psi )]} }}\\&={\underset {\mathrm {surprise} }{\underbrace {-\log p(s)} }}+{\underset {\mathrm {divergence} }{\underbrace {\mathbb {KL} [q({\dot {\psi }}\mid s,a,\mu ,\psi )\parallel p_{\text{Bayes}}({\dot {\psi }}\mid s,a,\mu ,\psi )]} }}\\&\geq {\underset {\mathrm {surprise} }{\underbrace {-\log p(s)} }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79cb2e8de6a300308d27a3f3d57f752de677151e)

![{\displaystyle \mathbb {KL} [q\parallel p_{\text{Bayes}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a49d443f70554490ab0a4f9394f0bf6f72c4d6d)





![{\displaystyle \lim _{T\to \infty }{\frac {1}{T}}{\underset {\text{free-action}}{\underbrace {\int _{0}^{T}F(s(t),\mu (t))\,dt} }}\geq \lim _{T\to \infty }{\frac {1}{T}}\int _{0}^{T}{\underset {\text{surprise}}{\underbrace {-\log p(s(t)\mid m)} }}\,dt=H[p(s\mid m)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45e9af1ac3447400ff76b1a3d8d09dbae0ea2542)
![{\displaystyle {\underset {\text{free-energy}}{\underbrace {F(s,\mu )} }}={\underset {\text{complexity}}{\underbrace {D_{\mathrm {KL} }[q(\psi \mid \mu )\parallel p(\psi \mid m)]} }}-{\underset {\mathrm {accuracy} }{\underbrace {E_{q}[\log p(s\mid \psi ,m)]} }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1485673d77ce7c702ff0e37885de968ebae63e26)




























