ÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį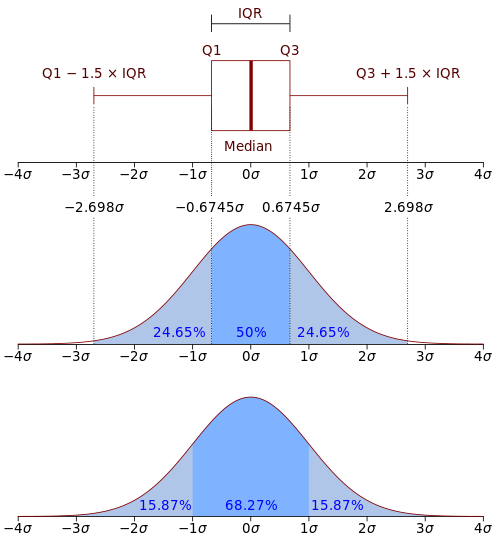 šĺč„Āą„ĀįŚćėŚ§Čśēį„ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„āíŚĻ≥ťĚĘšłä„Āģ„āį„É©„Éē„Āꍰ®ÁŹĺ„Āó„Ā¶„ÄĀxŤĽł„ĀęÁĘļÁéጧȜēį„ĀģŚÄ§„āí„ÄĀyŤĽł„ĀęÁĘļÁéáŚĮÜŚļ¶„āíśé°„Ā£„ĀüŚ†īŚźą„ÄĀśĪā„āĀ„Āü„ĀĄÁĮĄŚõ≤ÔľąxŚÄ§ÔľČ„ĀģšłčťôźŚÄ§„Ā®šłäťôźŚÄ§„Āß„ĀģŚěāÁõīÁ∑ö„Ā®„ÄĀŚ§Čśēį„āį„É©„Éēśõ≤Á∑ö„Ā® y = 0 „ĀģÁõīÁ∑ö„Ā®„Āߌõ≤„Āĺ„āĆ„āčÁĮĄŚõ≤„ĀģťĚĘÁ©ć„ĀĆÁĘļÁéá„Āę„Ā™„āč„Äā „ÄĆÁĘļÁéጹ܌łÉťĖĘśēį„Äć (probability distribution function)[1] „Āā„āč„ĀĄ„ĀĮ„ÄĆÁĘļÁéáťĖĘśēį„Äć (probability function)[2] „Ā®„ĀĄ„ĀÜÁĒ®Ť™ě„ĀĮ„ÄĀŚÖ∑šĹďÁöĄ„ĀęšĹē„āíśĆá„Āó„Ā¶„ĀĄ„āč„ĀčÁŹĺśôāÁāĻ„Āß„āāŚģöÁĺ©„ĀĆśõĖśėß„Āß„Āā„āä„ÄĀÁĘļÁéáŤęĖÁ†ĒÁ©∂ŤÄÖ„āĄÁĶĪŤ®ąŚ≠¶ŤÄÖ„ĀģťĖď„Āß„ĀĮ„ÄĀ„ĀĚ„ĀģśĄŹŚĎ≥„ĀĆś®ôśļĖÁöĄ„Āß„Ā™„ĀĄ„Ā®„Āē„āĆ„ā茆īŚźą„ĀĆ„Āā„āč„Äā šĽĖ„ĀģŤ≥áśĖô„Āęśč†„āĆ„Āį„ÄĆÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„Äć„ĀĮŚÄ§„ĀģťõÜŚźą„ĀęŚĮĺ„Āô„āčťĖĘśēį„Ā®„Āó„Ā¶ŚģöÁĺ©„Āē„āĆ„Āü„āä„ÄĀÁīĮÁ©ćŚąÜŚłÉťĖĘśēį„Ā®„ĀģťĖĘšŅā„Āߍ®ÄŚŹä„Āē„āĆ„Āü„āä„ÄĀÁĘļÁéáŤ≥™ťáŹťĖĘśēį„ĀģśĄŹŚĎ≥„ĀßšĹŅ„āŹ„āĆ„Āü„āä„Āô„āč„Äā„Āē„āČ„Āę„ĀĮ„ÄĀŚĮÜŚļ¶ťĖĘśēį (density function) „Ā®„ĀĄ„ĀÜÁĒ®Ť™ě„ĀĆÁĘļÁéáŤ≥™ťáŹťĖĘśēį„ĀģśĄŹŚĎ≥„ĀßÁĒ®„ĀĄ„āČ„āĆ„Ā¶„ĀĄ„ā茆īŚźą„āā„Āā„āč[3]„Äā šĺčšĺč„Ā®„Āó„Ā¶„ÄĀŚĮŅŚĎĹ„ĀĆ4„Äú6śôāťĖďÁ®čŚļ¶„Āģ„Éź„āĮ„ÉÜ„É™„āĘ„ĀĆ„ĀĄ„āč„Ā®šĽģŚģö„Āô„āč„Äā„Āď„Āģśôā„ÄĀÁČĻŚģö„Āģ„Éź„āĮ„ÉÜ„É™„āĘ„ĀĆšłĀŚļ¶ 5śôāťĖď„Āßś≠Ľšļ°„Āô„āčÁĘļÁéá„ĀĮ„Ā©„āĆšĹć„Ā†„āć„ĀÜ„ĀčÔľü Á≠Ē„Āą„ĀĮ0%„Āß„Āā„āč„Äā„Āä„āą„ĀĚ5śôāťĖď„ĀߌĮŅŚĎĹ„āíŤŅé„Āą„āč„Éź„āĮ„ÉÜ„É™„āĘ„ĀĮ„Āü„ĀŹ„Āē„āďŚĪÖ„āč„ĀĆ„ÄĀś≠£ÁĘļ„Āę5.0000000000‚ĶśôāťĖď„Āßś≠Ľ„Ā¨„Āď„Ā®„ĀĮ„Ā™„ĀĄ„Äā šłÄśĖĻ„Āß„ÄĀ5„Äú5.01śôāťĖď„Āßś≠Ľšļ°„Āô„āčÁĘļÁéá„ĀĮ„Ā©„ĀÜ„Ā†„āć„ĀÜ„ĀčÔľü šĺč„Āą„Āį„ÄĀ„Āď„āĆ„ĀĆ2%„Ā†„Ā®„Āô„āč„Äā„Āß„ĀĮ„ÄĀ„ĀĚ„Āģ1/10„ĀģÁĮĄŚõ≤„Āģ5„Äú5.001śôāťĖď„Āß„Āā„āčÁĘļÁéá„ĀĮÔľü Á≠Ē„Āą„ĀĮ„Āä„āą„ĀĚ 2% √ó 1/10 = 0.2% „Ā®„Ā™„āč„Äā„Āē„āČ„Āę„ĀĚ„Āģ 1/10 „ĀģÁĮĄŚõ≤„Āģ5„Äú5.0001śôāťĖď„Āß„Āā„āčÁĘļÁéá„ĀĮ„ÄĀ„Āä„āą„ĀĚ0.02%„Āß„Āā„āč„Äā šłäŤ®ė„Āģ3šĺč„Āę„Āä„ĀĄ„Ā¶„ÄĀ„Äé„ÄĆÁČĻŚģö„ĀģśôāťĖďÁĮĄŚõ≤ŚÜÖ„Āęś≠Ľšļ°„Āô„āčÁĘļÁéá„Äć„āí„ÄĆ„ĀĚ„ĀģÁĮĄŚõ≤„Āģťē∑„Āē„Äć„ĀߌČ≤„Ā£„ĀüŚÄ§„ÄŹ„ĀęÁĚÄÁõģ„Āô„āč„Ā®„ÄĀ1śôāťĖď„Āę„Ā§„Āć 2 „ĀęŚģö„Āĺ„āč„Āď„Ā®„ĀĆŚąÜ„Āč„āč„Äāšĺč„Āą„Āį„ÄĀ5„Äú5.01śôāťĖď„Āģ0.01śôāťĖď„ĀģÁĮĄŚõ≤„Āß„Éź„āĮ„ÉÜ„É™„āĘ„ĀĆś≠Ľšļ°„Āô„āčÁĘļÁéá„ĀĮ0.02„Āß„Āā„āä„ÄĀÁĘļÁéá 0.02 √∑ 0.01śôāťĖď = 2śôāťĖď‚ąí1 „Āß„Āā„āč„Äā„Āď„Āģ2śôāťĖď‚ąí1ÔľąśĮéśôā200%ԾȄĀ®„ĀĄ„ĀܝᏄāí„ÄĀ5śôāťĖďśôāÁāĻ„Āß„ĀģÁĘļÁéáŚĮÜŚļ¶„Ā®ŚĎľ„Ā∂„Äā Śĺď„Ā£„Ā¶„ÄĀ„ÄĆ„Éź„āĮ„ÉÜ„É™„āĘ„ĀģŚĮŅŚĎĹ„ĀĆ5śôāťĖď„Āß„Āā„āčÁĘļÁéá„Äć„āíŚēŹ„āŹ„āĆ„Āüśôā„ÄĀÁúü„ĀģÁ≠Ē„Āą„ĀĮ0%„Āß„Āā„āč„ĀĆ„ÄĀ„āą„āäŚģüÁĒ®ÁöĄ„Āę„ĀĮ„ÄĀ2śôāťĖď‚ąí1 dt „Āß„Āā„āč„Ā®Ť®Ä„Āą„āč„Äā„Āď„āĆ„ĀĮ„ÄĀÁĄ°ťôźŚįŹ„ĀģśôāťĖďÁĮĄŚõ≤ dt ŚÜÖ„Āß„ÄĀ„Éź„āĮ„ÉÜ„É™„āĘ„ĀĆś≠Ľšļ°„Āô„āčÁĘļÁéá„Āß„Āā„āč„Äāšĺč„Āą„Āį„ÄĀšłĀŚļ¶5śôāťĖď„Äú5śôāťĖď + 1„Éä„ÉéÁßí„ĀģŚĮŅŚĎĹ„Āß„Āā„āčÁĘļÁéá„ĀĮ„ÄĀ2śôāťĖď‚ąí1 √ó 1„Éä„ÉéÁßí ‚Čą 6 √ó 10‚ąí13 „Āß„Āā„āč„Äā „Āď„āĆ„āíÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį f „āíÁĒ®„ĀĄ„Ā¶„ÄĀfÔľą5śôāťĖďÔľČ= 2śôāťĖď‚ąí1 „Ā®Ť°®ÁŹĺ„Āô„āč„Āď„Ā®„ĀĆ„Āß„Āć„āč„Äāf „ā횼ĽśĄŹ„ĀģśôāťĖďÁĮĄŚõ≤ÔľąŚĺģŚįŹ„Āęťôź„āČ„Ā™„ĀĄÔľČ„ĀßÁ©ćŚąÜ„Āô„āč„Āď„Ā®„Āß„ÄĀŚĹ≤śôāťĖďÁĮĄŚõ≤ŚÜÖ„Āß„Éź„āĮ„ÉÜ„É™„āĘ„ĀģŚĮŅŚĎĹ„ĀĆŚįĹ„Āć„āčÁĘļÁéá„āíśĪā„āĀ„āč„Āď„Ā®„ĀĆ„Āß„Āć„āč„Äā ÁĶ∂ŚĮĺťÄ£Á∂öÁĘļÁéጹ܌łÉ„Āß„ĀģŚģöÁĺ©‚Üí„ÄĆťÄ£Á∂öÁĘļÁéጹ܌łÉ„Äć„āāŚŹāÁÖß
ÁĶ∂ŚĮĺťÄ£Á∂öÁĘļÁéጹ܌łÉ„Āß„ĀĮÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„ĀĆŚ≠ėŚú®„Āô„āč„ÄāÁĘļÁéጧȜēį X „ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį fX „āíŤÄÉ„Āą„ÄĀfX „ĀĆťĚěŤ≤†„Āģ„Éę„Éô„Éľ„āįŚŹĮÁ©ćŚąÜ„Ā™ťĖĘśēį„Āß„Āā„āč„Ā®„Āô„āč„Äā„Āď„Āď„Āß„ÄĀ „Āß„Āā„āč„ÄāŚĺď„Ā£„Ā¶„ÄĀ„āā„Āó FX „āí X „ĀģÁīĮÁ©ćŚąÜŚłÉťĖĘśēį„Ā®„Āô„āč„Ā®„ÄĀ „Ā®„Ā™„āä„ÄĀ „Ā®„Ā™„āč„ÄāÁõīŤ¶≥ÁöĄ„Āę„ÄĀŚĺģŚįŹŚĆļťĖď [x, x + dx] „Āꌟę„Āĺ„āĆ„āčŚÄ§„āí X „ĀĆ„Ā®„āčÁĘļÁéá„ĀĮ fX(x)dx „Āß„Āā„āč„Ā®ŚąÜ„Āč„āč„Äā ś≠£ŚľŹ„Ā™ŚģöÁĺ©
ŚģĆŚÖ®Śä†ś≥ēśóŹ ÔľąťÄöŚłł„ÄĀRn „ĀꌏĮśł¨ťõÜŚźą„Ā®„Āó„Ā¶„Éú„ɨ„ÉęťõÜŚźą„āíŤÄÉ„Āą„Āü„āā„ĀģԾȚł≠„ĀęŚ≠ėŚú®„Āô„āčÁĘļÁéጧȜēį X „ĀĮ„ÄĀ šł≠„Āęśł¨Śļ¶ X‚ąóP „ĀßÁĘļÁéጹ܌łÉ„Āô„āč„Äā šł≠„Āģś®ôśļĖśł¨Śļ¶ őľ „ĀęťĖĘ„Āô„āč X „ĀģŚĮÜŚļ¶„ĀĮ„ÄĀ„É©„ÉČ„É≥Ծ̄Éč„ā≥„Éá„ā£„Ɇ„ĀģŚģöÁźÜ„āą„āä „Āß„Āā„āč„Äā„Āď„āĆ„ĀĮ„ÄĀf „ĀĮś¨°„ĀģśÄߍ≥™„āíśĆĀ„Ā§šĽĽśĄŹ„ĀģŚŹĮśł¨ťĖĘśēį„Āß„Āā„āč„Āď„Ā®„ā휥ŹŚĎ≥„Āô„āč„Äā„Āā„āČ„āÜ„ā茏Įśł¨ťõÜŚźą „ĀęŚĮĺ„Āó„Ā¶„ÄĀ ś≥®śĄŹÁāĻšłäŤ®ė„ĀģťÄ£Á∂öŚćėŚ§Čśēį„ĀģŚ†īŚźą„ĀĮ„ÄĀś®ôśļĖśł¨Śļ¶„ĀĮ„Éę„Éô„Éľ„āįśł¨Śļ¶„Āß„Āā„āč„ÄāťõĘśē£ÁĘļÁéጧȜēį„Āę„Āä„ĀĎ„āčÁĘļÁéáŤ≥™ťáŹťĖĘśēį„ĀĮś®ôśú¨Á©ļťĖďÔľąťÄöŚłł„ÄĀśēīśēįŚÖ®šĹď„ĀģťõÜŚźą„Āĺ„Āü„ĀĮ„ĀĚ„ĀģťÉ®ŚąÜťõÜŚźąÔľČŚÜÖ„Āß„Āģśēį„Āąšłä„Āíśł¨Śļ¶„ĀęŚĮĺŚŅú„Āô„āč„Äā šĽĽśĄŹ„Āģśł¨Śļ¶„ĀߌĮÜŚļ¶„ĀĆŚģöÁĺ©„Āß„Āć„ā荮≥„Āß„ĀĮ„Ā™„ĀĄ„Āď„Ā®„Āęś≥®śĄŹ„Äāšĺč„Āą„Āį„ÄĀťÄ£Á∂öÁĘļÁéጹ܌łÉ„Āęśēį„Āąšłä„Āíśł¨Śļ¶„āíŚĮĺŚŅú„Āē„Āõ„āč„Āď„Ā®„ĀĮ„Āß„Āć„Ā™„ĀĄ„Äā„Āē„āČ„Āę„ÄĀŚĮĺŚŅú„Āô„āčśł¨Śļ¶„ĀĆŚ≠ėŚú®„Āó„Āüśôā„ÄĀŚĮÜŚļ¶„ĀĮ„ĀĽ„Ā®„āď„Ā©Ťá≥„āč„Ā®„Āď„āć„ĀßšłÄśĄŹÁöĄ„Āß„Āā„āč„Äā Ť©≥ÁīįÁĘļÁéáŤ≥™ťáŹťĖĘśēį„Ā®„ĀĮÁēį„Ā™„āä„ÄĀÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„ĀĮ1„āą„ā䌧߄Āć„Ā™ŚÄ§„ā팏Ė„āä„ĀÜ„āč„Äāšĺč„Āą„Āį„ÄĀŚĆļťĖď [0, 1/2] „ĀģťÄ£Á∂öšłÄśßėŚąÜŚłÉ„ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„ĀĮÁĮĄŚõ≤ 0 ‚ȧ x ‚ȧ 1/2 „Āß f(x) = 2„ÄĀ„ĀĚ„ĀģšĽĖ„ĀģÁĮĄŚõ≤„Āß f(x) = 0 „Āß„Āā„āč„Äā ś≠£Ť¶ŹŚąÜŚłÉ„ĀĮšłčŤ®ė„ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„āíśĆĀ„Ā§„Äā ÁĘļÁéጧȜēį X „Ā®„ĀĚ„ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį f „ĀĆšłé„Āą„āČ„āĆ„Āüśôā„ÄĀX „ĀģśúüŚĺ֌ħ„ĀĮÔľąŚÄ§„ĀĆŚ≠ėŚú®„Āô„ā茆īŚźą„ĀĮԾȜ¨°„ĀģŚľŹ„ĀßśĪā„āĀ„āČ„āĆ„āč„Äā ŚÖ®„Ā¶„ĀģÁĘļÁéጹ܌łÉ„ĀĆÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„āíśĆĀ„Ā§„Ā®„ĀĮťôź„āČ„Ā™„ĀĄ„ÄāťõĘśē£ŚěčÁĘļÁéጧȜēį„ĀĆśĆĀ„Āü„Ā™„ĀĄšĽĖ„Āę„āā„ÄĀ„āę„É≥„Éą„Éľ„Éꌹ܌łÉ„ĀĮťÄ£Á∂öÁĘļÁéጹ܌łÉ„Āß„Āā„āč„Āę„āā„Āč„Āč„āŹ„āČ„Āö„ÄĀÁĮĄŚõ≤ŚÜÖ„Āģ„Āā„āČ„āÜ„āčÁāĻ„Āßś≠£„ĀģÁĘļÁéá„āíśĆĀ„Āü„Ā™„ĀĄ„Āü„āĀ„ÄĀÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„āíśĆĀ„Āü„Ā™„ĀĄ„Äā ÁĘļÁéጹ܌łÉ„ĀĮ„ĀĚ„ĀģÁīĮÁ©ćŚąÜŚłÉťĖĘśēį F(x) „ĀĆÁĶ∂ŚĮĺťÄ£Á∂ö„Āß„Āā„ā茆īŚźą„Āę„Āģ„ĀŅÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį f „āíśĆĀ„Ā§„Äā„Āď„ĀģŚ†īŚźą F „ĀĮ„ĀĽ„Ā®„āď„Ā©Ťá≥„āč„Ā®„Āď„āć„ĀߌĺģŚąÜŚŹĮŤÉĹ„Āß„ÄĀf „ĀĮ F „Āģ„É©„ÉČ„É≥=„Éč„ā≥„Éá„ā£„Ɇ„ĀģŚģöÁźÜ„Āß„Āā„āčÔľö ÁīĮÁ©ćŚąÜŚłÉťĖĘśēį„ĀĆťÄ£Á∂ö„ĀģŚ†īŚźą„ÄĀÁĘļÁéጧȜēį„ĀĆ„Āā„āčŚÄ§ a „āí„Ā®„āčÁĘļÁéá P(X = a) „ĀĮŚłł„Āę0„Āß„Āā„āč„Äā 2„Ā§„ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį f, g „ĀĆ„ĀĽ„Ā®„āď„Ā©Ťá≥„āč„Ā®„Āď„āć„ĀßÁ≠Č„Āó„ĀĄśôā„ÄĀ2„Ā§„ĀĮś≠£ÁĘļ„ĀꌟƄĀėÁĘļÁéጹ܌łÉ„Āč„āČśé°„āČ„āĆ„Āü„Ā®Ť®Ä„Āą„āč„Äā ÁĶĪŤ®ąŚäõŚ≠¶„ĀģŚąÜťáé„Āß„ĀĮ„ÄĀÁīĮÁ©ćŚąÜŚłÉťĖĘśēį„Āģ„É©„ÉČ„É≥=„Éč„ā≥„Éá„ā£„ɆŚĺģŚąÜ„Ā®ÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„Ā®„ĀģťĖĘšŅā„āíťĚěŚĹĘŚľŹÁöĄ„Āęśõł„ĀĄ„ĀüšĽ•šłč„ĀģŚľŹ„ĀĆÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„ĀģŚģöÁĺ©„Ā®„Āó„Ā¶ÁĒ®„ĀĄ„āČ„āĆ„āč„Äā dt „ĀĆÁĄ°ťôźŚįŹ„Āģśôā„ÄĀX „ĀĆŚĆļťĖďÔľąt, t + dtԾȄĀꌟę„Āĺ„āĆ„āčÁĘļÁéá„ĀĮ f(t)dt „ĀęÁ≠Č„Āó„ĀĄ„Äā ťõĘśē£ŚąÜŚłÉ„Ā®ťÄ£Á∂öŚąÜŚłÉ„Ā®„ĀģÁĶźŚźą„Éá„ā£„É©„ÉÉ„āĮ„Āģ„Éá„Éę„āŅťĖĘśēį„āíÁĒ®„ĀĄ„āč„Ā®„ÄĀ„Āā„āčÁ®ģ„ĀģťõĘśē£ŚěčÁĘļÁéጧȜēį„Āę„āą„Ā£„Ā¶ťÄ£Á∂öŚěčÁĘļÁéጧȜēį„Āä„āą„Ā≥ťõĘśē£ŚěčÁĘļÁéጧȜēį„ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„āíÁĶĪšłÄÁöĄ„Āꍰ®ÁŹĺ„Āô„āč„Āď„Ā®„ĀĆ„Āß„Āć„āč„ÄāŤ©¶„Āó„Āę„ÄĀ2„Ā§„ĀģŚÄ§„Āó„Āčśé°„āČ„Ā™„ĀĄťõĘśē£ŚěčÁĘļÁéጧȜēį„āíŤÄÉ„Āą„āč„Äāšĺč„Āą„Āį„É©„Éľ„Éá„Éě„ÉÉ„Éė„Éꌹ܌łÉ‚Äē„Āô„Ā™„āŹ„Ā°„ĀĚ„āĆ„Āě„āĆ 1/2 „ĀģÁĘļÁéá„Āß ‚ąí1 „Āĺ„Āü„ĀĮ 1 „ĀģŚÄ§„āíśé°„ā茹܌łÉ‚Äē„Āß„Āā„āč„Äā„Āď„ĀģŚ§Čśēį„ĀģÁĘļÁéá„ĀģŚĮÜŚļ¶„ĀĮ „Āß„Āā„āč„Äā„āą„ā䚳蹨ŚĆĖ„Āô„āč„Ā®„ÄĀťõĘśē£Ś§Čśēį„ĀĆ n ťÄö„āä„ĀģŚģüśēįŚÄ§„ā팏Ė„āäŚĺó„āčśôā„ÄĀ„ĀĚ„ĀģťõĘśē£ŚÄ§„āí x1, ‚Ķ, xn, „ĀĚ„ĀģÁĘļÁéá„āí p1, ‚Ķ, pn „Ā®„Āô„āč„Ā®ÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„ĀĮ „Ā®Ť°®Ť®ė„Āē„āĆ„āč„Äā „Āď„āĆ„ĀĮŚģüŤ≥™ÁöĄ„Āę„ÄĀťõĘśē£ŚěčÁĘļÁéጧȜēį„Ā®ťÄ£Á∂öŚěčÁĘļÁéጧȜēį„āíÁĶĪŚźą„Āó„Ā¶„ĀĄ„āč„Äāšĺč„Ā®„Āó„Ā¶„ÄĀšłäŤ®ė„ĀģŤ°®ÁŹĺ„Āč„āČ„ĀĮťÄ£Á∂öŚ§Čśēį„Ā®ŚźĆśßė„ĀęťõĘśē£Ś§Čśēį„Āę„Ā§„ĀĄ„Ā¶ÁĶĪŤ®ąŚ≠¶ÁöĄ„ÉĎ„É©„É°„Éľ„āŅÔľąŚĻ≥ŚĚá„ÄĀŚąÜśē£„ÄĀŚįĖŚļ¶„Ā™„Ā©ÔľČ„ā퍮ąÁģóŚŹĮŤÉĹ„Āß„Āā„āč„Äā „ÉĎ„É©„É°„Éľ„āŅŚĆĖÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„Āĺ„Āü„ĀĮÁĘļÁéáŤ≥™ťáŹťĖĘśēį„ā횼ĽśĄŹ„ĀģŚ™íšĽčŚ§Čśēį„Āß„ÉĎ„É©„É°„Éľ„āŅŚĆĖ„Āô„āč„Āď„Ā®„ĀĆ„Āó„Āį„Āó„Āį„Āā„āč„Äāšĺč„Āą„Āį„ÄĀś≠£Ť¶ŹŚąÜŚłÉ„ĀģŚĮÜŚļ¶„ĀĮŚĻ≥ŚĚá őľ „Āä„āą„Ā≥ŚąÜśē£ ŌÉ2 „āíÁĒ®„ĀĄ„Ā¶šłčŤ®ė„Āģ„āą„ĀÜ„Āꍰ®ÁŹĺ„Āß„Āć„āč„Äā „Āď„Āģ„Ā®„ĀćŚĮÜŚļ¶„ĀģśóŹ„ĀģŚģöÁĺ©Śüü„Ā®śóŹ„Āģ„ÉĎ„É©„É°„Éľ„āŅ„ĀģŚģöÁĺ©Śüü„Ā®„ĀģťĀē„ĀĄ„ĀęÁēôśĄŹ„Āô„āč„Āď„Ā®„ĀĆťá捶Ā„Āß„Āā„āč„Äā„ÉĎ„É©„É°„Éľ„āŅ„ĀģŚÄ§„ĀĆÁēį„Ā™„āč„Ā®„ÄĀŚźĆ„Āėś®ôśú¨Á©ļťĖďÔľąŚ§Čśēį„ĀĆŚŹĖ„āäŚĺó„āčŚÖ®„Ā¶„ĀģŚÄ§„ĀģťõÜŚźą„Āß„ÄĀŚźĆšłÄ„Āß„Āā„āčԾȄĀęŚĪě„Āô„āčÁēį„Ā™„āčÁĘļÁéጧȜēį„ĀģŚąÜŚłÉ„ā퍰®ÁŹĺ„Āô„āč„Āď„Ā®„Āę„Ā™„āč„Äā„ĀĚ„Āģś®ôśú¨Á©ļťĖď„ĀĮ„ÄĀ„ĀĚ„ĀģŚąÜŚłÉ„ĀģśóŹ„ĀĆÁ§ļ„Āó„Ā¶„ĀĄ„āčÁĘļÁéጧȜēį„ĀģśóŹ„ĀģŚģöÁĺ©Śüü„Āß„Āā„āč„Äāšłé„Āą„āČ„āĆ„Āü„ÉĎ„É©„É°„Éľ„āŅ„ĀģťõÜŚźą„ĀĮ„ÄĀ„ĀĚ„Āģ„ÉĎ„É©„É°„Éľ„āŅ„āíÁĒ®„ĀĄ„ĀüŚÖĪťÄö„ĀģťĖĘśēį„Ā®„Āó„Ā¶ÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„ā퍮ėŤŅį„Āß„Āć„āčÁĘļÁéጹ܌łÉśóŹ„ĀģŚÜÖ„Āģ1„Ā§„āíśĆá„Āô„ÄāÁĘļÁéጹ܌łÉ„ĀģŤ¶≥ÁāĻ„Āč„āČ„Āô„āč„Ā®„ÄĀ„ÉĎ„É©„É°„Éľ„āŅ„ĀĮŚģöśēį„Ā™„Āģ„Āß„ÄĀÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„ĀꌧȜēį„ā팟ę„Āĺ„Āö„ÉĎ„É©„É°„Éľ„āŅ„Āģ„ĀŅ„ā팟ę„āÄŚ†īŚźą„ÄĀ„ÉĎ„É©„É°„Éľ„āŅ„ĀĮŚąÜŚłÉ„Āģś≠£Ť¶ŹŚĆĖšŅāśēįÔľąŚģöÁĺ©ŚüüŚÖ®Śüü„Āß„ĀģÁĘļÁéá=1„Āę„Ā™„āčśßė„ĀꍙŅśēī„Āô„āčšŅāśēįԾȄĀģšłÄťÉ®„āíśąź„Āô„Äā„Āď„Āģś≠£Ť¶ŹŚĆĖšŅāśēį„ĀĮŚąÜŚłÉ„Āģ„āę„Éľ„Éć„ÉęÔľąŤčĪŤ™ěÁȹԾȌ§Ė„Āę„Āā„āč„Äā „ÉĎ„É©„É°„Éľ„āŅ„ĀĆŚģöśēį„Ā™„Āģ„Āß„ÄĀ„Āē„āČ„ĀęÁēį„Ā™„āč„ÉĎ„É©„É°„Éľ„āŅ„ĀߌÜć„ÉĎ„É©„É°„Éľ„āŅŚĆĖ„Āó„Ā¶śóŹ„Āģšł≠„ĀꚼĖ„ĀģÁĘļÁéጧȜēį„āíšĹćÁĹģšĽė„ĀĎ„āč„Āď„Ā®„ĀĮ„ÄĀŚćė„Āꌏ§„ĀĄ„ÉĎ„É©„É°„Éľ„āŅ„āíść®„Ā¶„Ā¶ŚľŹ„Āģšł≠„ĀęśĖį„Āó„ĀĄ„ÉĎ„É©„É°„Éľ„āŅ„āíÁĹģ„ĀŹ„Ā†„ĀĎ„ĀęťĀé„Āé„Ā™„ĀĄ„Äā„Āó„Āč„Āó„ÄĀÁĘļÁéáŚĮÜŚļ¶„ĀģŚģöÁĺ©Śüü„ā팧Ȝõī„Āô„āč„Āď„Ā®„Āę„ĀĮśÖéťáć„Āē„ĀĆŚŅÖŤ¶Ā„Āß„ÄĀšĹúś•≠ťáŹ„ĀĆŚ§ö„ĀŹ„Ā™„āč„ÄāšłčŤ®ė„Āģ#ŚĺďŚĪ쌧Ȝēį„Ā®Ś§ČśēįŚ§ČśŹõś¨Ą„ā팏āÁÖß„Äā Ś§öŚ§ČťáŹ„ĀęťĖĘ„Āô„āčÁĘļÁéáŚĮÜŚļ¶ťĖĘśēįŚźĆśôāÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį‚Üí„ÄĆŚźĆśôāŚąÜŚłÉ„Äć„āāŚŹāÁÖß
nŚÄč„ĀģťÄ£Á∂öŚěčÁĘļÁéጧȜēį X1, ‚Ķ, Xn „Āę„Ā§„ĀĄ„Ā¶„ÄĀŚźĆśôāÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„Ā®ŚĎľ„Āį„āĆ„āčÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„āíŚģöÁĺ©„Āô„āč„Āď„Ā®„ĀĆ„Āß„Āć„āč„Äā„Āď„ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„ĀĮ nś¨°ŚÖÉÁ©ļťĖď„ĀģŚģöÁĺ©Śüü D šł≠„Āģ n ŚÄč„ĀģŚ§Čśēį X1, ‚Ķ, Xn „āíÁĒ®„ĀĄ„Ā¶„ÄĀšłčŤ®ė„Āģ„āą„ĀÜ„Āęśõł„ĀŹ„Āď„Ā®„ĀĆ„Āß„Āć„āč„Äā „āā„Āó F (x1, ‚Ķ, xn) = Pr(X1 ‚ȧ x1, ‚Ķ, Xn ‚ȧ xn) „ĀĆ„Éô„āĮ„Éą„Éę (X1, ‚Ķ, Xn) „ĀģŚźĆśôāÁīĮÁ©ćŚąÜŚłÉťĖĘśēį„Ā™„āČ„Āį„ÄĀŚźĆśôāÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„āíŚĀŹŚĺģŚąÜ„Āߌįé„ĀŹ„Āď„Ā®„ĀĆ„Āß„Āć„āč„Äā ŚĎ®ŤĺļÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį‚Üí„ÄĆŚĎ®ŤĺļŚąÜŚłÉ„Äć„āāŚŹāÁÖß
i = 1, 2, ‚Ķ, n „Āģśôā„ÄĀfXi(xi) „ā팧Ȝēį Xi „Āģ„ĀŅ„ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„Ā®„Āô„āč„Äā„Āď„āĆ„ĀĮŚĎ®ŤĺļÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„Ā®ŚĎľ„Āį„āĆ„ÄĀÁĘļÁéጧȜēį X1, ‚Ķ, Xn „ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„Āč„āČ Xi šĽ•Ś§Ė„Āģ n ‚ąí 1 ŚÄč„ĀģŚ§Čśēį„āíťáćÁ©ćŚąÜ„Āô„āč„Āď„Ā®„ĀßśĪā„āĀ„āČ„āĆ„āč„Äā Áč¨Áę茟ƜôāÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„āíśßčśąź„Āô„āčťÄ£Á∂öŚěčÁĘļÁéጧȜēį X1, ‚Ķ, Xn „ĀĆ„ĀĄ„Āö„āĆ„āāÁč¨Áęč„Āß„Āā„āčśôā„ÄĀ „Āß„Āā„āč„Äā„ĀĚ„āĆ„Āě„āĆ„ĀģŚĎ®ŤĺļÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„ĀĮšłčŤ®ė„Āߍ°®„Āē„āĆ„āč„Äā šĺ蚼•šłč„Āę2Ś§Čśēį„Āß„ĀģŚüļśú¨ÁöĄ„Ā™šĺč„ā퍮ė„Āô„Äā2ś¨°ŚÖÉ„ĀģÁĘļÁéá„Éô„āĮ„Éą„Éę (X, Y) „āí „Ā®„Āô„āč„Ā®„ÄĀx, y „ĀĆŚÖĪ„Āęś≠£„Āß„Āā„āčÁ¨¨IŤĪ°ťôź„Āߌĺó„āČ„āĆ„Āü „ĀģÁĘļÁéá„ĀĮ „Āß„Āā„āč„Äā ŚĺďŚĪ쌧Ȝēį„Ā®Ś§ČśēįŚ§ČśŹõÁĘļÁéጧȜēį X „ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„ĀĆ fX(x) „Āß„Āā„āčśôā„ÄĀŚą•Ś§Čśēį„ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį Y = g(X) „ā퍮ąÁģó„Āô„āč„Āď„Ā®„ĀĆ„Āß„Āć„āč„ÄāÔľąŚ§ö„ĀŹ„ĀģŚ†īŚźą„ĀĮŚŅÖŤ¶Ā„Ā™„ĀĄ„ĀĆ„ÄāԾȄĀď„āĆ„ĀĮ„ÄĆŚ§ČśēįŚ§ČśŹõ„Äć„Ā®ŚĎľ„Āį„āĆ„ÄĀŚģüťöõťĚĘ„Āß„ĀĮśóĘÁü•„ĀģÔľąšłÄśßėŚąÜŚłÉÁ≠ČԾȚĻĪśēįÁĒüśąźŚô®„Āč„āČšĽĽśĄŹ„ĀģŚĹĘ„Āģ fg(X) = fY „āíŚįé„ĀćŚáļ„Āô„Āď„Ā®„ĀĆ„Āß„Āć„āč„Äā ťĖĘśēį g „ĀĆŚćėŤ™ŅŚÜôŚÉŹ„Āß„Āā„āčśôā„ÄĀ„ĀĚ„ĀģÁĶźśěúŚĺó„āČ„āĆ„āčÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„ĀĮ „Āß„Āā„āč„Äā„Āď„Āď„Āß g‚ąí1 „ĀĮťÄÜŚÜôŚÉŹ„Āß„Āā„āč„Äā „Āď„Āģ„Āď„Ā®„ĀĮŚĺģŚąÜÁĮĄŚõ≤„Āꌟę„Āĺ„āĆ„āčÁĘļÁéá„ĀĆŚ§ČśēįŚ§ČśŹõŚĺĆ„āāšłćŚ§Č„Āß„Āā„āč„Āď„Ā®„Āč„āČ„āāŚąÜ„Āč„āč„Äā„Ā§„Āĺ„āä„ÄĀ „Āĺ„Āü„ĀĮ „Āß„Āā„āč„ÄāšłÄśĖĻ„ÄĀŚćėŤ™ŅŚÜôŚÉŹ„Āß„Ā™„ĀĄÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį y „ĀĮ Ôľąn(y) „ĀĮg(x) = y „āíśļÄ„Āü„Āô x „ĀģŤß£„Āģśēį„ÄĀgk‚ąí1(y) „ĀĮ„ĀĚ„ĀģŤß£ÔľČ„Āß„Āā„āč„Äā „Āď„āĆ„ā퍶č„āč„Ā®„ÄĀśúüŚĺ֌ħ E[g(X)] „āíśĪā„āĀ„āč„Āü„āĀ„Āę„ĀĮśúÄŚąĚ„ĀęśĖį„Āü„Ā™ÁĘļÁéጧȜēį Y = g(X) „ĀģÁĘļÁéáŚĮÜŚļ¶ fg(X) „āíśĪā„āĀ„āčŚŅÖŤ¶Ā„ĀĆ„Āā„āč„Ā®śÄĚ„ĀĄ„Āü„ĀŹ„Ā™„āč„Äā„Āó„Āč„Āó„ÄĀ „ā퍮ąÁģó„Āô„āč„āą„āä„ĀĮ„āÄ„Āó„āć„ÄĀ „ā퍮ąÁģó„Āô„āčśĖĻ„ĀĆ„āą„ĀĄ„Äā X „Ā® g(X) „Āģšł°śĖĻ„ĀĆÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„āíśĆĀ„Ā§śôā„ÄĀ„Āā„āČ„āÜ„ā茆īŚźą„Āę2„Ā§„ĀģÁ©ćŚąÜŚÄ§„ĀĮÁ≠Č„Āó„ĀĄ„Äāg „ĀĆŚćėŚįĄ„Āß„Āā„āčŚŅÖŤ¶Ā„ĀĮ„Ā™„ĀĄ„ÄāŚČćŤÄÖ„āą„āäŚĺĆŤÄÖ„ĀģŤ®ąÁģó„ĀĆÁį°Śćė„Āß„Āā„ā茆īŚźą„ĀĆ„Āā„āč„Äā Ś§öŚ§ČťáŹšłäŤ®ė„ĀģŚľŹ„ĀĮ„ÄĀ1„Ā§„āą„āä„āāŚ§ö„ĀŹ„ĀģŚ§Čśēį„ĀęšĺĚŚ≠ė„Āô„ā茧ȜēįÔľąy „Ā®śõł„ĀŹÔľČ„Āꚳ蹨ŚĆĖ„Āß„Āć„āč„Äāy „ĀĆšĺĚŚ≠ė„Āô„ā茧Ȝēį„ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„āí f(x1, ‚Ķ, xn) „Ā®„Āô„āč„Ā®„ÄĀšĺĚŚ≠ėťĖĘšŅā„ĀĮ y = g(x1, ‚Ķ, xn) „Āߍ°®„Āē„āĆ„āč„Äā„Āď„Āģ„Ā®„ĀćŚĺó„āČ„āĆ„āčÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„ĀĮ[Ť¶ĀŚáļŚÖł] „Ā®„Ā™„āč„Äā„Āü„Ā†„ĀóÁ©ćŚąÜ„ĀĮś∑Ľ„ĀąŚ≠ó„ĀģśĖĻÁ®čŚľŹ„Āģ (n ‚ąí 1) ś¨°ŚÖÉ„ĀģŤß£ŚÖ®šĹď„āíśł°„āä„ÄĀŤ®ėŚŹ∑ dV „ĀĮŚģüťöõ„ĀģŤ®ąÁģó„Āę„ĀĮ„Āď„ĀģŤß£„Āģ„ÉĎ„É©„É°„Éľ„āŅŚĆĖ„ĀęÁĹģ„Ā朏õ„Āą„Ā™„ĀĎ„āĆ„Āį„Ā™„āČ„Ā™„ĀĄ„ÄāŚ§Čśēį x1, ‚Ķ, xn „ĀĮ„āā„Ā°„āć„āď„Āď„Āģ„ÉĎ„É©„É°„Éľ„āŅŚĆĖ„ĀģťĖĘśēį„Āß„Āā„āč„Äā „Āď„āĆ„Āč„āČ„āą„āäÁõīśĄüÁöĄ„Ā™Ť°®ÁŹĺ„ĀĆŚįé„Āč„āĆ„āč„Äāx „ā팟ƜôāÁĘļÁéáŚĮÜŚļ¶ f „Āģ n ś¨°ŚÖÉÁĘļÁéጧȜēį„Ā®„Āô„āč„ÄāH „āíŚÖ®ŚćėŚįĄ„ĀߌĺģŚąÜŚŹĮŤÉĹ„Ā™ťĖĘśēį„Ā®„Āó„Ā¶ y = H(x) „Āß„Āā„āč„Ā™„āČ„Āį„ÄĀy „ĀĮŚĮÜŚļ¶ g „āíśĆĀ„Ā§Ôľö „Āď„Āď„ĀߌĺģŚąÜ„ĀĮ H „ĀģťÄÜťĖĘśēį„Āģ„ɧ„ā≥„Éƌąó„Āģ y „Āę„Āä„ĀĎ„āčŚÄ§„Āß„Āā„āč„Äā Áč¨ÁęčśÄß„ā횼ģŚģö„Āó„Ā¶„Éá„Éę„āŅťĖĘśēį„āíÁĒ®„ĀĄ„āč„Ā®„ÄĀšĽ•šłč„Āģ„āą„ĀÜ„ĀꌟƄĀėÁĶźśěú„ĀĆŚĺó„āČ„āĆ„āč„Äā Áč¨Áęč„Ā™ÁĘļÁéጧȜēį Xi, i = 1, 2, ‚Ķn „ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„ĀĆ fXi(xi) „Āßšłé„Āą„āČ„āĆ„āčśôā„ÄĀY = G(X1, X2, ‚ĶXn) „ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„ā퍮ąÁģó„Āß„Āć„āč„Äāś¨°„ĀģŚľŹ„ĀĮ„ÄĀY „ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį fY(y) „Ā® fXi(xi) „āí„Éá„Éę„āŅťĖĘśēį„ĀßÁĶźŚźą„Āô„āč„āā„Āģ„Āß„Āā„āč„Äā Áč¨Áęč„Ā™ÁĘļÁéጧȜēį„ĀģŚíĆ„ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį‚Üí„ÄĆÁē≥„ĀŅŤĺľ„ĀŅ„Äć„āāŚŹāÁÖß
2„Ā§„ĀģÁč¨Áęč„Ā™ÁĘļÁéጧȜēį U „Ā® V „ĀĆ„ĀĚ„āĆ„Āě„āĆÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„āíśĆĀ„Ā§śôā„ÄĀŚíĆ U + V „ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„ĀĮšł°ÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„ĀģÁē≥„ĀŅŤĺľ„ĀŅ„Āߍ°®„Āē„āĆ„āč„Äā „Āď„ĀģťĖĘšŅā„ĀĮ„ÄĀNŚÄč„ĀģÁč¨Áęč„Ā™ÁĘļÁéጧȜēį U1, ‚Ķ, UN „ĀģŚíĆ„Āęśč°ŚľĶ„Āß„Āć„āč„Äā „Āď„āĆ„ĀĮšłčŤ®ė„ĀęÁ§ļ„ĀôÁč¨Áęč„Ā™ÁĘļÁéጧȜēį„ĀģŚēÜ„ĀģŚ†īŚźą„Ā®ŚźĆśßė„Āę„ÄĀ2ťÄö„āä„ĀģŚ§ČśēįŚ§ČśŹõ Y = U + V „Ā® Z = V „Āč„āČŚįé„Āč„āĆ„āč„Äā Áč¨Áęč„Ā™ÁĘļÁéጧȜēį„ĀģÁ©ć„Ā®ŚēÜ„ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį2„Ā§„ĀģÁč¨Áęč„Ā™ÁĘļÁéጧȜēį U „Ā® V „ĀĆ„ĀĚ„āĆ„Āě„āĆÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„āíśĆĀ„Ā§śôā„ÄĀÁ©ć UV „Ā®ŚēÜ U/V „ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„ā팧ȜēįŚ§ČśŹõ„Āę„āą„Ā£„Ā¶Ť®ąÁģó„Āô„āč„Āď„Ā®„ĀĆ„Āß„Āć„āč„Äā ŚēÜ„ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį2„Ā§„ĀģÁč¨Áęč„Ā™ÁĘļÁéጧȜēį U „Ā® V „ĀģŚēÜ Y = U/V „ĀĮ„ÄĀś¨°„Āģ„āą„ĀÜ„ĀꌧȜŹõ„Āē„āĆ„āč„Äā „Āď„Āģśôā„ÄĀŚźĆśôāÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį p(Y, Z) „ĀĮ U, V „āí Y, Z „ĀꌧȜēįŚ§ČśŹõ„Āô„āč„Āď„Ā®„Āߍ®ąÁģó„Āß„Āć„ÄĀY „ĀĮŚźĆśôāÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„Āč„āČ Z „āíŚĎ®ŤĺļŚĆĖ„Āô„āč„Āď„Ā®„ĀߌįéŚáļ„Āß„Āć„āč„Äā „ĀĚ„ĀģťÄÜŚ§ČśŹõ„ĀĮ„ÄĀ „Āß„Āā„āč„Äā „Āď„ĀģŚ§ČśŹõ„Āģ„ɧ„ā≥„Éƌąó „ĀĮ„ÄĀ „Āß„Āā„āč„Äā Śĺď„Ā£„Ā¶„ÄĀ „Ā®„Ā™„āč„Äā Y „ĀģŚąÜŚłÉ„ĀĮ Z „ĀģŚĎ®ŤĺļŚĆĖ„Āę„āą„Ā£„Ā¶„ÄĀ „Ā®Ť®ąÁģó„Āē„āĆ„āč„Äā „Āď„ĀģśČčś≥ē„Āß U, V „āí Y, Z „ĀꌧȜŹõ„Āô„āčśôā„Āꚳ挏Įś¨†„Ā™śĚ°šĽ∂„ĀĆŚÖ®ŚćėŚįĄ„Āß„Āā„āč„ÄāšłäŤ®ė„ĀģŚ§ČśŹõ„ĀĮ Z „ĀĆ V „ĀęÁõīśé•ťÄÜŚÜôŚÉŹ„Āē„āĆ„ÄĀšłé„Āą„āČ„āĆ„Āü V „Āę„Ā§„ĀĄ„Ā¶ U/V „ĀĆŚćėŤ™ŅŚÜôŚÉŹ„Āß„Āā„āč„Āģ„Āߜ̰šĽ∂„ĀęťĀ©Śźą„Āó„Ā¶„ĀĄ„āč„Äā„Āď„āĆ„ĀĮ„ÄĀŚíĆÔľöU + V, Ś∑ģÔľöU ‚ąí V„ÄĀÁ©ćÔľöUV „Āę„Āä„ĀĄ„Ā¶„āāŚźĆśßė„Āß„Āā„āč„Äā Áč¨Áęč„Ā™ÁĘļÁéጧȜēį„ĀģÁ©ć„Āę„Ā§„ĀĄ„Ā¶„āāŚÖ®„ĀŹŚźĆ„ĀėśČčś≥ē„Āߍ®ąÁģó„Āô„āč„Āď„Ā®„ĀĆ„Āß„Āć„āč„Äā šĺčÔľö2„Ā§„Āģś®ôśļĖś≠£Ť¶ŹŚąÜŚłÉ„ĀģśĮĒ„ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēįś®ôśļĖś≠£Ť¶ŹŚąÜŚłÉ„ĀęŚĺď„ĀÜÁĘļÁéጧȜēį U, V „Āę„Ā§„ĀĄ„Ā¶„ÄĀ„ĀĚ„ĀģśĮĒÔľąŚēÜԾȄĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„ĀĮś¨°„Āģ„āą„ĀÜ„ĀęśĪā„āĀ„āČ„āĆ„āč„Äā „Āĺ„Āö„ÄĀÁĘļÁéጧȜēį„ĀĮ„ĀĚ„āĆ„Āě„āĆšłčŤ®ė„ĀģÁĘļÁéáŚĮÜŚļ¶ťĖĘśēį„āíśĆĀ„Ā§„Äā „Āď„āĆ„āíŚÖą„ĀęŤŅį„ĀĻ„Āü„āą„ĀÜ„ĀꌧȜŹõ„Āô„āč„Äā „Āď„āĆ„Āč„āČ„ÄĀ „ĀĆŚįé„Āč„āĆ„āč„Äā„Āď„āĆ„ĀĮ„ÄĀś®ôśļĖ„ā≥„Éľ„ā∑„ÉľŚąÜŚłÉ„Āß„Āā„āč„Äā ťĖĘťÄ£ť†ÖÁõģ
ŚáļŚÖł
śĖáÁĆģ
Ś§ĖťÉ®„É™„É≥„āĮ
|
Portal di Ensiklopedia Dunia








![{\displaystyle \operatorname {E} [X]=\int _{-\infty }^{\infty }x\,f(x)\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91e3fa656d4fd0a4c5b754f25203e105efd15ef9)




![{\displaystyle f(x;\mu ,\sigma ^{2})={\frac {1}{\sigma {\sqrt {2\pi }}}}\exp {\biggl [}-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}{\biggr ]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95e4f8bda207562f7c90ef2f31b9e7dbf0bebdb1)











![{\displaystyle \operatorname {E} [g(X)]=\int _{-\infty }^{\infty }yf_{g(X)}(y)\,dy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/996bc41d8f620112c17234ca8f7b3f2593be87fd)
![{\displaystyle \operatorname {E} [g(X)]=\int _{-\infty }^{\infty }g(x)f_{X}(x)\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50fb3681bf7d2c3cff167c44eb62534ecf69d617)
















![{\displaystyle {\begin{aligned}p(Y)&=\int _{-\infty }^{\infty }p_{U}(YZ)\,p_{V}(Z)\,|Z|\,dZ\\&=\int _{-\infty }^{\infty }{\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}Y^{2}Z^{2}}{\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}Z^{2}}|Z|\,dZ\\&=\int _{-\infty }^{\infty }{\frac {1}{2\pi }}e^{-{\frac {1}{2}}(Y^{2}+1)Z^{2}}|Z|\,dZ\\&=2\int _{0}^{\infty }{\frac {1}{2\pi }}e^{-{\frac {1}{2}}(Y^{2}+1)Z^{2}}Z\,dZ\\&=\int _{0}^{\infty }{\frac {1}{\pi }}e^{-(Y^{2}+1)u}\,du&&u={\tfrac {1}{2}}Z^{2}\\&=\left.-{\frac {1}{\pi (Y^{2}+1)}}e^{-(Y^{2}+1)u}\right]_{u=0}^{\infty }\\&={\frac {1}{\pi (Y^{2}+1)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10770de156debb5b0ab958b3cf2018de6577e8a8)













