žąėŽ°† Í≥ľ ž°įŪē©Ž°† žóźžĄú, ŽęľŽĻĄžöįžä§ Ūē®žąė (M√∂biusŚáĹśēł, žėĀžĖī : M√∂bius function )ŽäĒ ž†ēžąėÍįÄ ž†úÍ≥Ī žĚłžąėÍįÄ žóÜŽäĒ ž†ēžąė žĚłžßÄ žó¨Ž∂Äžóź ŽĒįŽĚľ Ž∂ĄŽ•ėŪēėŽäĒ Í≥ĪžÖąž†Ā Ūē®žąė žĚīŽč§. ŽęľŽĻĄžöįžä§ Žįėž†Ą Í≥ĶžčĚ žóź žā¨žö©ŽźėŽ©į, Ž¶¨ŽßĆ ÍįÄžĄ§ Í≥ľŽŹĄ ÍĻäžĚÄ ÍīÄÍ≥ĄŽ•ľ ÍįĞߥŽč§. ÍłįŪėłŽäĒ
őľ
(
n
)
{\displaystyle \mu (n)}
ŽęľŽĻĄžöįžä§ Ūē®žąė
őľ
:
Z
+
‚Üí
{
‚ąí
1
,
0
,
+
1
}
{\displaystyle \mu \colon \mathbb {Z} ^{+}\to \{-1,0,+1\}}
ŽäĒ žĖĎžĚė ž†ēžąė
n
‚ąą
Z
+
{\displaystyle n\in \mathbb {Z} ^{+}}
{
‚ąí
1
,
0
,
1
}
{\displaystyle \{-1,0,1\}}
n
{\displaystyle n}
k
{\displaystyle k}
ž†úÍ≥Ī žĚłžąėÍįÄ žóÜŽäĒ ž†ēžąė ŽĚľŽ©ī
őľ
(
n
)
=
(
‚ąí
1
)
k
{\displaystyle \mu (n)=(-1)^{k}}
n
=
1
{\displaystyle n=1}
őľ
(
1
)
=
1
{\displaystyle \mu (1)=1}
n
{\displaystyle n}
ž†úÍ≥Ī žĚłžąėÍįÄ žóÜŽäĒ ž†ēžąė ÍįÄ žēĄŽčąŽĚľŽ©ī,
őľ
(
n
)
=
0
{\displaystyle \mu (n)=0}
ž¶Č,
n
{\displaystyle n}
žÜƞ̳žąė Ž∂ĄŪēī ÍįÄ
n
=
‚ąŹ
p
p
n
p
{\displaystyle n=\prod _{p}p^{n_{p}}}
ŽĚľŽ©ī, ŽęľŽĻĄžöįžä§ Ūē®žąėŽäĒ Žč§žĚĆÍ≥ľ ÍįôŽč§.
őľ
(
n
)
=
(
‚ąí
1
)
‚ąĎ
p
n
p
‚ąŹ
p
[
n
p
‚ȧ
1
]
{\displaystyle \mu (n)=(-1)^{\sum _{p}n_{p}}\prod _{p}[n_{p}\leq 1]}
žó¨ÍłįžĄú
[
‚čĮ
]
{\displaystyle [\cdots ]}
žēĄžĚīŽ≤Ąžä® ÍīĄŪėł (ž°įÍĪīžĚī žįłžĚīŽ©ī 1, žēĄŽčąŽ©ī 0)žĚīŽč§.
ŽęľŽĻĄžöįžä§ Ūē®žąė
őľ
(
n
)
{\displaystyle \mu (n)}
1žĚė žõźžčúž†Ā
n
{\displaystyle n}
žĚė Ūē©žĚīŽč§.
őľ
(
n
)
=
‚ąĎ
1
‚ȧ
k
‚ȧ
n
gcd
{
k
,
n
}
=
1
exp
‚Ā°
(
2
ŌÄ
i
k
/
n
)
{\displaystyle \mu (n)=\sum _{\scriptstyle 1\leq k\leq n \atop \scriptstyle \gcd\{k,n\}=1}\exp(2\pi ik/n)}
ž¶ĚŽ™Ö (ŪŹ¨Ūē®Žįįž†úžĚė žõźŽ¶¨žĚĄ ŪÜĶŪēú ž¶ĚŽ™Ö):
Žč§žĚĆÍ≥ľ ÍįôžĚÄ Ūē≠ŽďĪžčĚžĚī žĄĪŽ¶ĹŪēúŽč§.
‚ąĎ
k
=
1
n
exp
‚Ā°
(
2
ŌÄ
i
k
/
n
)
=
őī
n
,
1
=
{
1
n
=
1
0
n
>
1
{\displaystyle \sum _{k=1}^{n}\exp(2\pi ik/n)=\delta _{n,1}={\begin{cases}1&n=1\\0&n>1\end{cases}}}
ŪŹ¨Ūē®Žįįž†úžĚė žõźŽ¶¨ žóź ŽĒįŽĚľ, Žč§žĚĆžĚī žĄĪŽ¶ĹŪēúŽč§.
őľ
(
n
)
=
‚ąĎ
d
‚ą£
n
őľ
(
d
)
őī
n
/
d
,
1
=
‚ąĎ
d
‚ą£
n
őľ
(
d
)
‚ąĎ
k
=
1
n
/
d
exp
‚Ā°
(
2
ŌÄ
i
d
k
/
n
)
=
‚ąĎ
k
=
1
n
exp
‚Ā°
(
2
ŌÄ
i
k
/
n
)
‚ąí
‚ąĎ
p
‚ą£
n
‚ąĎ
k
=
1
n
/
p
exp
‚Ā°
(
2
ŌÄ
i
p
k
/
n
)
+
‚ąĎ
p
,
q
‚ą£
n
p
‚Ȇ
q
‚ąĎ
k
=
1
n
/
p
q
exp
‚Ā°
(
2
ŌÄ
i
p
q
k
/
n
)
‚ąí
‚čĮ
=
‚ąĎ
1
‚ȧ
k
‚ȧ
n
gcd
{
k
,
n
}
=
1
exp
‚Ā°
(
2
ŌÄ
i
k
/
n
)
{\displaystyle {\begin{aligned}\mu (n)&=\sum _{d\mid n}\mu (d)\delta _{n/d,1}\\&=\sum _{d\mid n}\mu (d)\sum _{k=1}^{n/d}\exp(2\pi idk/n)\\&=\sum _{k=1}^{n}\exp(2\pi ik/n)-\sum _{p\mid n}\sum _{k=1}^{n/p}\exp(2\pi ipk/n)+\sum _{\scriptstyle p,q\mid n \atop \scriptstyle p\neq q}\sum _{k=1}^{n/pq}\exp(2\pi ipqk/n)-\cdots \\&=\sum _{\scriptstyle 1\leq k\leq n \atop \scriptstyle \gcd\{k,n\}=1}\exp(2\pi ik/n)\end{aligned}}}
ž¶ĚŽ™Ö (ž§ĎÍĶ≠žĚłžĚė ŽāėŽ®łžßÄ ž†ēŽ¶¨Ž•ľ ŪÜĶŪēú ž¶ĚŽ™Ö):
žöįžĄ†, žöįŽ≥Ä
f
(
n
)
{\displaystyle f(n)}
n
{\displaystyle n}
Í≥ĪžÖąž†Ā Ūē®žąė žěĄžĚĄ Ž≥īžĚīžěź.
exp
‚Ā°
(
2
ŌÄ
i
)
=
1
{\displaystyle \exp(2\pi i)=1}
k
‚Č°
k
′
(
mod
n
)
{\displaystyle k\equiv k'{\pmod {n}}}
ŽĚľŽ©ī
exp
‚Ā°
(
2
ŌÄ
i
k
/
n
)
=
exp
‚Ā°
(
2
ŌÄ
i
k
′
/
n
)
{\displaystyle \exp(2\pi ik/n)=\exp(2\pi ik'/n)}
žĚīŽč§. ŽĒįŽĚľžĄú, žöįŽ≥ÄžĚė Ūē©žĚÄ Žč§žĚĆÍ≥ľ ÍįôžĚī Žč§žčú žďł žąė žěąŽč§.
f
(
n
)
=
‚ąĎ
k
‚ąą
(
Z
/
(
n
)
)
√ó
exp
‚Ā°
(
2
ŌÄ
i
k
/
n
)
{\displaystyle f(n)=\sum _{k\in (\mathbb {Z} /(n))^{\times }}\exp(2\pi ik/n)}
žĚīž†ú,
n
{\displaystyle n}
žÜƞ̳žąė Ž∂ĄŪēī ÍįÄ
n
=
p
1
a
1
‚čĮ
p
r
a
r
{\displaystyle n=p_{1}^{a_{1}}\cdots p_{r}^{a_{r}}}
ŽĚľÍ≥† Ūēėžěź. ž§ĎÍĶ≠žĚłžĚė ŽāėŽ®łžßÄ ž†ēŽ¶¨ žóź ŽĒįŽĚľ, ÍįĀ
i
‚ąą
{
1
,
…
,
r
}
{\displaystyle i\in \{1,\dots ,r\}}
e
i
‚Č°
1
(
mod
p
i
a
i
)
{\displaystyle e_{i}\equiv 1{\pmod {p_{i}^{a^{i}}}}}
e
i
‚Č°
0
(
mod
p
j
a
j
)
(
j
‚Ȇ
i
)
{\displaystyle e_{i}\equiv 0{\pmod {p_{j}^{a_{j}}}}\qquad (j\neq i)}
žĚł žú†žĚľŪēú
e
i
‚ąą
Z
/
(
n
)
{\displaystyle e_{i}\in \mathbb {Z} /(n)}
(
k
1
,
…
,
k
r
)
↦
k
1
e
1
+
‚čĮ
k
r
e
r
{\displaystyle (k_{1},\dots ,k_{r})\mapsto k_{1}e_{1}+\cdots k_{r}e_{r}}
žĚÄ ÍĶį ŽŹôŪėē žā¨žÉĀ
(
Z
/
(
p
1
a
1
)
)
√ó
√ó
‚čĮ
√ó
(
Z
/
(
p
r
a
r
)
)
√ó
‚Üí
(
Z
/
(
n
)
)
√ó
{\displaystyle (\mathbb {Z} /(p_{1}^{a_{1}}))^{\times }\times \cdots \times (\mathbb {Z} /(p_{r}^{a_{r}}))^{\times }\to (\mathbb {Z} /(n))^{\times }}
žĚĄ žĚīŽ£®Ž©į, ŪäĻŪěą žĚīŽäĒ ž†ĄŽč®žā¨ Ūē®žąė žĚīŽč§. Žßąžį¨ÍįÄžßÄŽ°ú,
k
i
↦
e
i
k
i
{\displaystyle k_{i}\mapsto e_{i}k_{i}}
ŽäĒ ÍĶįžĚė žěźÍłį ŽŹôŪėē žā¨žÉĀ
(
Z
/
(
p
i
a
i
)
)
√ó
‚Üí
(
Z
/
(
p
i
a
i
)
)
√ó
{\displaystyle (\mathbb {Z} /(p_{i}^{a_{i}}))^{\times }\to (\mathbb {Z} /(p_{i}^{a_{i}}))^{\times }}
žĚĄ žĚīŽ£®Ž©į, ŪäĻŪěą žĚīŽäĒ ž†ĄŽč®žā¨ Ūē®žąė žĚīŽč§. ŽĒįŽĚľžĄú,
f
(
n
)
=
‚ąĎ
k
1
‚ąą
(
Z
/
(
p
1
a
1
)
)
√ó
‚čĮ
‚ąĎ
k
1
‚ąą
(
Z
/
(
p
1
a
1
)
)
√ó
exp
‚Ā°
(
2
ŌÄ
i
(
k
1
e
1
+
‚čĮ
+
k
r
e
r
)
/
n
)
=
(
‚ąĎ
k
1
‚ąą
(
Z
/
(
p
1
a
1
)
)
√ó
exp
‚Ā°
(
2
ŌÄ
i
k
1
e
1
/
n
)
)
‚čĮ
(
‚ąĎ
k
1
‚ąą
(
Z
/
(
p
1
a
1
)
)
√ó
exp
‚Ā°
(
2
ŌÄ
i
k
r
e
r
/
n
)
)
=
(
‚ąĎ
k
1
‚ąą
(
Z
/
(
p
1
a
1
)
)
√ó
exp
‚Ā°
(
2
ŌÄ
i
k
1
/
n
)
)
‚čĮ
(
‚ąĎ
k
1
‚ąą
(
Z
/
(
p
1
a
1
)
)
√ó
exp
‚Ā°
(
2
ŌÄ
i
k
r
/
n
)
)
=
f
(
p
1
a
1
)
‚čĮ
f
(
p
r
a
4
)
{\displaystyle {\begin{aligned}f(n)&=\sum _{k_{1}\in (\mathbb {Z} /(p_{1}^{a_{1}}))^{\times }}\cdots \sum _{k_{1}\in (\mathbb {Z} /(p_{1}^{a_{1}}))^{\times }}\exp(2\pi i(k_{1}e_{1}+\cdots +k_{r}e_{r})/n)\\&=\left(\sum _{k_{1}\in (\mathbb {Z} /(p_{1}^{a_{1}}))^{\times }}\exp(2\pi ik_{1}e_{1}/n)\right)\cdots \left(\sum _{k_{1}\in (\mathbb {Z} /(p_{1}^{a_{1}}))^{\times }}\exp(2\pi ik_{r}e_{r}/n)\right)\\&=\left(\sum _{k_{1}\in (\mathbb {Z} /(p_{1}^{a_{1}}))^{\times }}\exp(2\pi ik_{1}/n)\right)\cdots \left(\sum _{k_{1}\in (\mathbb {Z} /(p_{1}^{a_{1}}))^{\times }}\exp(2\pi ik_{r}/n)\right)\\&=f(p_{1}^{a_{1}})\cdots f(p_{r}^{a_{4}})\end{aligned}}}
žĚīŽč§.
žĚīž†ú, žÜĆžąė
p
{\displaystyle p}
a
‚ąą
Z
+
{\displaystyle a\in \mathbb {Z} ^{+}}
f
(
p
a
)
=
őľ
(
p
a
)
{\displaystyle f(p^{a})=\mu (p^{a})}
f
(
p
a
)
=
‚ąĎ
1
‚ȧ
k
‚ȧ
p
a
gcd
{
k
,
p
}
=
1
exp
‚Ā°
(
2
ŌÄ
i
k
/
p
a
)
=
‚ąĎ
k
=
1
p
a
exp
‚Ā°
(
2
ŌÄ
i
k
/
p
a
)
‚ąí
‚ąĎ
k
=
1
p
a
‚ąí
1
exp
‚Ā°
(
2
ŌÄ
i
k
/
p
a
‚ąí
1
)
=
{
‚ąí
1
a
=
1
0
a
>
1
{\displaystyle {\begin{aligned}f(p^{a})&=\sum _{\scriptstyle 1\leq k\leq p^{a} \atop \scriptstyle \gcd\{k,p\}=1}\exp(2\pi ik/p^{a})\\&=\sum _{k=1}^{p^{a}}\exp(2\pi ik/p^{a})-\sum _{k=1}^{p^{a-1}}\exp(2\pi ik/p^{a-1})\\&={\begin{cases}-1&a=1\\0&a>1\end{cases}}\end{aligned}}}
őľ
{\displaystyle \mu }
Ž©ĒŽ•īŪÖźžä§ Ūē®žąė (MertensŚáĹśēł, žėĀžĖī : Mertens function )ŽäĒ ŽęľŽĻĄžöįžä§ Ūē®žąėžĚė Ž∂ÄŽ∂ĄŪē©žĚīŽč§. ž¶Č, Žč§žĚĆÍ≥ľ ÍįôžĚÄ Ūē®žąėžĚīŽč§.
M
:
Z
+
‚Üí
Z
{\displaystyle M\colon \mathbb {Z} ^{+}\to \mathbb {Z} }
M
(
n
)
=
‚ąĎ
k
=
1
n
őľ
(
k
)
{\displaystyle M(n)=\sum _{k=1}^{n}\mu (k)}
ŽęľŽĻĄžöįžä§ Ūē®žąėŽäĒ 1žĚė žõźžčúž†Ā
n
{\displaystyle n}
žĚė Ūē©žĚīŽĮÄŽ°ú, Ž©ĒŽ•īŪÖźžä§ Ūē®žąėŽ•ľ Žč§žĚĆÍ≥ľ ÍįôžĚī ž†ēžĚėŪē† žąėŽŹĄ žěąŽč§.
M
(
n
)
=
‚ąĎ
a
‚ąą
F
n
exp
‚Ā°
(
2
ŌÄ
i
a
)
{\displaystyle M(n)=\sum _{a\in {\mathcal {F}}_{n}}\exp(2\pi ia)}
žó¨ÍłįžĄú
F
n
{\displaystyle {\mathcal {F}}_{n}}
n
{\displaystyle n}
ŪéėŽ¶¨ žąėžóī žĚīŽč§.
ŽęľŽĻĄžöįžä§ Ūē®žąėŽäĒ Í≥ĪžÖąž†Ā Ūē®žąė žĚīŽč§. ž¶Č, žĄúŽ°úžÜĆ ž†ēžąėžóź ŽĆÄŪēėžó¨ Žč§žĚĆÍ≥ľ ÍįôŽč§.
őľ
(
a
b
)
=
őľ
(
a
)
őľ
(
b
)
(
gcd
{
a
,
b
}
=
1
)
{\displaystyle \mu (ab)=\mu (a)\mu (b)\qquad (\gcd\{a,b\}=1)}
ŽęľŽĻĄžöįžä§ Ūē®žąėŽäĒ ŽĒĒŽ¶¨ŪĀīŽ†ą Ūē©žĄĪÍ≥Ī žēĄŽěė žÉĀžąė Ūē®žąė 1žĚė žó≠žõźžĚīŽč§.
(
őľ
‚ąó
1
)
(
n
)
=
‚ąĎ
d
‚ą£
n
őľ
(
d
)
=
őī
n
,
1
=
{
1
n
=
1
0
n
>
1
{\displaystyle (\mu *1)(n)=\sum _{d\mid n}\mu (d)=\delta _{n,1}={\begin{cases}1&n=1\\0&n>1\end{cases}}}
žĚī žĄĪžßą ŽēĆŽ¨łžóź ŽęľŽĻĄžöįžä§ Ūē®žąėŽäĒ ŽęľŽĻĄžöįžä§ Žįėž†Ą Í≥ĶžčĚ žóź ŽďĪžě•ŪēúŽč§.
ŽęľŽĻĄžöįžä§ Ūē®žąėžĚė žÉĚžĄĪ Ūē®žąė ŽäĒ Žč§žĚĆÍ≥ľ ÍįôŽč§.
‚ąĎ
n
=
1
‚ąě
őľ
(
n
)
x
n
=
x
‚ąí
‚ąĎ
a
=
2
‚ąě
x
a
+
‚ąĎ
a
=
2
‚ąě
‚ąĎ
b
=
2
‚ąě
x
a
b
‚ąí
‚ąĎ
a
=
2
‚ąě
‚ąĎ
b
=
2
‚ąě
‚ąĎ
c
=
2
‚ąě
x
a
b
c
+
‚ąĎ
a
=
2
‚ąě
‚ąĎ
b
=
2
‚ąě
‚ąĎ
c
=
2
‚ąě
‚ąĎ
d
=
2
‚ąě
x
a
b
c
d
‚ąí
‚čĮ
{\displaystyle \sum _{n=1}^{\infty }\mu (n)x^{n}=x-\sum _{a=2}^{\infty }x^{a}+\sum _{a=2}^{\infty }\sum _{b=2}^{\infty }x^{ab}-\sum _{a=2}^{\infty }\sum _{b=2}^{\infty }\sum _{c=2}^{\infty }x^{abc}+\sum _{a=2}^{\infty }\sum _{b=2}^{\infty }\sum _{c=2}^{\infty }\sum _{d=2}^{\infty }x^{abcd}-\cdots }
ŽęľŽĻĄžöįžä§ Ūē®žąėžĚė ŽěĆŽ≤†Ž•īŪäł ÍłČžąė ŽäĒ Žč§žĚĆÍ≥ľ ÍįôŽč§.
‚ąĎ
n
=
1
‚ąě
őľ
(
n
)
q
n
1
‚ąí
q
n
=
q
{\displaystyle \sum _{n=1}^{\infty }{\frac {\mu (n)q^{n}}{1-q^{n}}}=q}
žĚīŽäĒ
|
q
|
<
1
{\displaystyle |q|<1}
ŽęľŽĻĄžöįžä§ Ūē®žąėžĚė ŽĒĒŽ¶¨ŪĀīŽ†ą ͳȞąė ŽäĒ Ž¶¨ŽßĆ ž†úŪÉÄ Ūē®žąė žĚė žó≠žąėžĚīŽč§.
‚ąĎ
n
=
1
‚ąě
őľ
(
n
)
n
s
=
1
ő∂
(
s
)
{\displaystyle \sum _{n=1}^{\infty }{\frac {\mu (n)}{n^{s}}}={\frac {1}{\zeta (s)}}}
Ž©ĒŽ•īŪÖźžä§ ž∂Ēžł°žĚÄ Ž©ĒŽ•īŪÖźžä§ Ūē®žąėžĚė Í∑łŽěėŪĒĄÍįÄ ŪŹ¨Ž¨ľžĄ† žÜćžóź Ž®łŽ¨īŽ•łŽč§ŽäĒ ž∂Ēžł°žĚīŽč§. žĚīŽäĒ žěĎžĚÄ žąėžóź ŽĆÄŪēīžĄú žĄĪŽ¶ĹŪēėžßÄŽßĆ, Žß§žöį ŪĀį žąėžóź ŽĆÄŪēėžó¨ žĄĪŽ¶ĹŪēėžßÄ žēäŽäĒŽč§. ŽęľŽĻĄžöįžä§ Ūē®žąėžĚė ÍįížĚī
{
¬Ī
1
,
0
}
{\displaystyle \{\pm 1,0\}}
|
M
(
n
)
|
‚ȧ
n
‚ąÄ
n
‚ąą
Z
+
{\displaystyle |M(n)|\leq n\qquad \forall n\in \mathbb {Z} ^{+}}
žĚīŽč§.
žÜĆžąė ž†ēŽ¶¨ žóź ŽĒįŽĚľ Žč§žĚĆžĚī žĄĪŽ¶ĹŪēúŽč§.
lim
n
‚Üí
‚ąě
1
n
M
(
n
)
=
0
{\displaystyle \lim _{n\to \infty }{\frac {1}{n}}M(n)=0}
ŽėźŪēú, Žč§žĚĆžĚī žĄĪŽ¶ĹŪēúŽč§.
lim
n
‚Üí
‚ąě
1
n
‚ąĎ
k
=
0
n
|
őľ
(
n
)
|
=
‚ąŹ
p
(
1
‚ąí
1
p
2
)
=
1
ő∂
(
2
)
=
6
ŌÄ
2
{\displaystyle \lim _{n\to \infty }{\frac {1}{n}}\sum _{k=0}^{n}|\mu (n)|=\prod _{p}\left(1-{{1} \over {p^{2}}}\right)={{1} \over {\zeta (2)}}={{6} \over {\pi ^{2}}}}
ž¶Č, ž†źÍ∑ľž†ĀžúľŽ°ú
3
/
ŌÄ
2
‚Čą
30.4
%
{\displaystyle 3/\pi ^{2}\approx 30.4\%}
3
/
ŌÄ
2
‚Čą
30.4
%
{\displaystyle 3/\pi ^{2}\approx 30.4\%}
1
‚ąí
6
/
ŌÄ
2
‚Čą
39.2
%
{\displaystyle 1-6/\pi ^{2}\approx 39.2\%}
Ž¶¨ŽßĆ ÍįÄžĄ§ žĚÄ Ž©ĒŽ•īŪÖźžä§ Ūē®žąėžóź ŽĆÄŪēú Žč§žĚĆ ž°įÍĪīÍ≥ľ ŽŹôžĻė žĚīŽč§.
M
(
n
)
=
O
(
x
1
/
2
+
ŌĶ
)
‚ąÄ
ŌĶ
‚ąą
R
+
{\displaystyle M(n)=O(x^{1/2+\epsilon })\qquad \forall \epsilon \in \mathbb {R} ^{+}}
Ž©ĒŽ•īŪÖźžä§ ž∂Ēžł° (Mertensśé®śł¨, žėĀžĖī : Mertens conjecture )žĚÄ
‚ąÄ
n
‚ąą
Z
+
:
|
M
(
n
)
|
‚ȧ
n
{\displaystyle \forall n\in \mathbb {Z} ^{+}\colon |M(n)|\leq {\sqrt {n}}}
[ 1] [ 2] :188‚Äď189
lim‚ÄÜinf
M
(
n
)
n
<
‚ąí
1.009
{\displaystyle \liminf {\frac {M(n)}{\sqrt {n}}}<-1.009}
lim‚ÄÜsup
M
(
n
)
n
>
1.06
{\displaystyle \limsup {\frac {M(n)}{\sqrt {n}}}>1.06}
Í∑łŽü¨Žāė Ž¶¨ŽßĆ ÍįÄžĄ§ žĚÄ ŪėĄžě¨ (2021ŽÖĄ) ŽĮłŪēīÍ≤į Ž¨łž†úžĚīŽč§. Ž©ĒŽ•īŪÖźžä§ ž∂Ēžł°Ž≥īŽč§ ŽćĒ žēĹŪēėžßÄŽßĆ Ž¶¨ŽßĆ ÍįÄžĄ§Ž≥īŽč§ ŽćĒ ÍįēŪēú Ž™Öž†ú
M
(
x
)
=
O
(
x
1
/
2
)
{\displaystyle M(x)=O(x^{1/2})}
žó≠žčú žēĄžßĀ Žįėž¶ĚŽźėžßÄ žēäžēėžúľŽāė, žĚīŽäĒ žēĄŽßą ÍĪįžßďžĚľ Í≤ÉžĚīŽĚľÍ≥† ž∂Ēžł°ŽźúŽč§.[ 1]
ŽęľŽĻĄžöįžä§ Ūē®žąėžóź ŽĆÄŪēėžó¨ Žč§žĚĆÍ≥ľ ÍįôžĚÄ ÍłČžąėÍįÄ ž°īžě¨ŪēúŽč§.
‚ąĎ
n
=
1
‚ąě
(
őľ
(
n
)
/
n
)
2
=
15
/
ŌÄ
2
{\displaystyle \sum _{n=1}^{\infty }(\mu (n)/n)^{2}=15/\pi ^{2}}
‚ąĎ
n
=
1
‚ąě
őľ
(
n
)
ln
‚Ā°
n
n
=
‚ąí
1
{\displaystyle \sum _{n=1}^{\infty }\mu (n){\frac {\ln n}{n}}=-1}
ž≤ėžĚĆ Ž™á ÍįúžĚė žĖĎžĚė ž†ēžąėžóź ŽĆÄŪēīžĄú ŽęľŽĻĄžöįžä§ Ūē®žąėžôÄ Ž©ĒŽ•īŪÖźžä§ Ūē®žąėžĚė ÍįížĚÄ Žč§žĚĆÍ≥ľ ÍįôŽč§. (OEIS žĚė žąėžóī A008683 ), (OEIS žĚė žąėžóī A002321 )
n
{\displaystyle n}
1
2
3
4
5
6
7
8
9
10
11
12
őľ
(
n
)
{\displaystyle \mu (n)}
1
‚ąí1
‚ąí1
0
‚ąí1
1
‚ąí1
0
0
1
‚ąí1
0
M
(
n
)
{\displaystyle M(n)}
1
0
‚ąí1
‚ąí1
‚ąí2
‚ąí1
‚ąí2
‚ąí2
‚ąí2
‚ąí1
‚ąí2
‚ąí2
ŽęľŽĻĄžöįžä§ Ūē®žąėžĚė ÍįížĚė Í∑łŽěėŪĒĄŽäĒ Žč§žĚĆÍ≥ľ ÍįôŽč§.
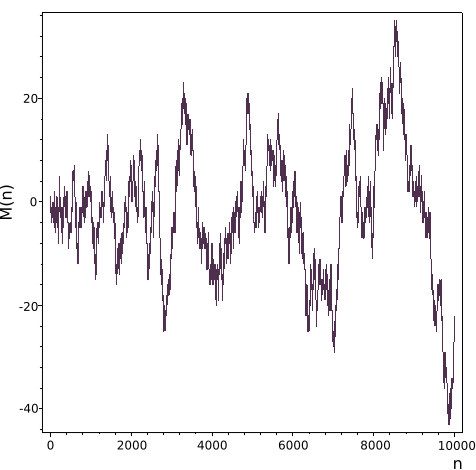
Ž©ĒŽ•īŪÖźžä§ Ūē®žąėžĚė 104 ÍĻĆžßÄžĚė ÍįížĚė Í∑łŽěėŪĒĄŽäĒ Žč§žĚĆÍ≥ľ ÍįôŽč§.
őľ
(
n
)
=
0
{\displaystyle \mu (n)=0}
n
{\displaystyle n}
ž†úÍ≥Ī žĚłžąėÍįÄ žóÜŽäĒ ž†ēžąė ÍįÄ žēĄŽčĆ žąė)žĚÄ Žč§žĚĆÍ≥ľ ÍįôŽč§.
4, 8, 9, 12, 16, 18, 20, 24, 25, 27, 28, 32, 36, 40, 44, 45, 48, 49, 50, 52, 54, 56, 60, 63, ‚Ķ (OEIS žĚė žąėžóī A013929 )
Ž†ąžė®ŪēėŽ•īŪäł žė§žĚľŽü¨ ŽäĒ 1748ŽÖĄ ž†ÄžĄú[ 3] [ 4] :99, Notes to ¬ß3.1 žĻīŽ•ľ ŪĒĄŽ¶¨ŽďúŽ¶¨Ūěą ÍįÄžöįžä§ ŽäĒ „Ääžāįžą† žóįÍĶ¨„Äč(ŽĚľŪčīžĖī : Disquisitiones Arithmeticae )[ 5] 1žĚė žõźžčú
n
{\displaystyle n}
žĚė Ūē©žĚī
őľ
(
n
)
{\displaystyle \mu (n)}
1831ŽÖĄžóź žēĄžöįÍĶ¨žä§Ūäł ŪéėŽ•īŽĒĒŽāúŪäł ŽęľŽĻĄžöįžä§ ŽäĒ ŽęľŽĻĄžöįžä§ Ūē®žąėŽ•ľ žĶúžīąŽ°ú Ž™Öžčúž†ĀžúľŽ°ú ŽŹĄžěÖŪēėžėÄŽč§.[ 6] [ 4] :99, Notes to ¬ß3.1 ŪĒĄŽěÄžł† Ž©ĒŽ•īŪÖźžä§ ÍįÄ žĶúžīąŽ°ú žė§ŽäėŽā† žā¨žö©ŽźėŽäĒ ÍłįŪėł őľŽ•ľ žā¨žö©ŪēėžėÄŽč§.[ 7] :53 [ 4] :99, Notes to ¬ß3.1
1885ŽÖĄ 7žõĒ 11žĚľžóź Ū܆Žßąžä§ žöĒžēĄŽĄąžä§ žä§ŪčłŪčįžĖīžä§ ŽäĒ žÉ§Ž•ľ žóźŽ•īŽĮłŪäł žóźÍ≤Ć Ž≥īŽāł ŪéłžßĞ󟞥ú Ž©ĒŽ•īŪÖźžä§ Ūē®žąėŽ•ľ žĶúžīąŽ°ú žā¨žö©ŪēėžėÄŽč§. (žĚī ŪéłžßÄŽäĒ 1905ŽÖĄžóź ž∂úŪĆźŽźėžóąŽč§.[ 8]
M
(
n
)
=
O
(
n
)
{\displaystyle M(n)=O({\sqrt {n}})}
|
M
(
n
)
|
‚ȧ
n
{\displaystyle |M(n)|\leq {\sqrt {n}}}
f
(
n
)
{\displaystyle f(n)}
g
(
n
)
{\displaystyle g(n)}
Í∑łŽü¨Žāė žä§ŪčłŪčįžĖīžä§ŽäĒ žĚī "ž¶ĚŽ™Ö"žĚĄ ž∂úŪĆźŪēėžßÄ žēäžēėŽč§.
1897ŽÖĄžóź ŪĒĄŽěÄžł† Ž©ĒŽ•īŪÖźžä§ ŽäĒ Ž©ĒŽ•īŪÖźžä§ Ūē®žąėŽ•ľ ŽŹÖžěźž†ĀžúľŽ°ú žě¨ŽįúÍ≤¨ŪēėžėÄÍ≥†, Ž©ĒŽ•īŪÖźžä§ ž∂Ēžł°žĚĄ žä§ŪčłŪčįžĖīžä§žôÄ ŽŹÖžěźž†ĀžúľŽ°ú ž∂Ēžł°ŪēėžėÄŽč§.[ 9]
1985ŽÖĄžóź žē§ŽďúŽ£® ŽßąžĚīŪĀī žė§Žď§Ž¶¨žä§žĹĒ(žėĀžĖī : Andrew Michael Odlyzko , 1949~)žôÄ Ū󧎕īŽßąŽČėžä§ žöĒŪēėŽĄąžä§ žöĒžĄúŪĒĄ ŪĄį Ž¶īŽü¨(ŽĄ§ŽćúŽěÄŽďúžĖī : Hermanus Johannes Joseph te Riele , 1947~)ŽäĒ Ž©ĒŽ•īŪÖźžä§ ž∂Ēžł°žĚī ÍĪįžßďžěĄžĚĄ ž¶ĚŽ™ÖŪēėžėÄŽč§.[ 1]
‚ÜĎ ÍįÄ Žāė Žč§ Odlyzko, A. M.; te Riele, H. J. J. (1985). ‚ÄúDisproof of the Mertens conjecture‚ÄĚ (PDF) . „ÄäJournal f√ľr die reine und angewandte Mathematik„Äč (žėĀžĖī) 357 : 138‚Äď160. doi :10.1515/crll.1985.357.138 . ISSN 0075-4102 . MR 783538 . Zbl 0544.10047 .
‚ÜĎ S√°ndor, J√≥zsef; Mitrinovińá, Dragoslav S.; Crstici, Borislav, ŪéłžßĎ. (2006). „ÄäHandbook of number theory I„Äč . Dordrecht: Springer. 187 ‚Äď189ž™Ĺ. ISBN 1-4020-4215-9 Zbl 1151.11300 . ‚ÜĎ Eulerus, Leonhardus (1748). „ÄäIntroductio in analysin infinitorum„Äč (ŽĚľŪčīžĖī). Ž°úžěĒ : Apud Marcum-Michaelem Bousquet & Socios. ‚ÜĎ ÍįÄ Žāė Žč§ Shapiro, Harold N. (1983). „ÄäIntroduction to the Theory of Numbers„Äč (žėĀžĖī). Wiley. ISBN 0-471-86737-3 ‚ÜĎ Gavss, Carolus Fridericus (1801). „ÄäDisqvisitiones arithmeticae„Äč (ŽĚľŪčīžĖī). ŽĚľžĚīŪĒĄžĻėŪěą : in commissis apvd Gerh. Fleischer, Jun. ‚ÜĎ M√∂bius, A. F. (1832). ‚Äú√úber eine besondere Art von Umkehrung der Reihen‚ÄĚ . „ÄäJournal f√ľr die reine und angewandte Mathematik„Äč (ŽŹÖžĚľžĖī) 1832 (9): 105-123. doi :10.1515/crll.1832.9.105 . ISSN 0075-4102 . Zbl 009.0333cj . ‚ÜĎ Mertens, F. (1874). ‚ÄúEin Beitrag zur analytischen Zahlentheorie‚ÄĚ . „ÄäJournal f√ľr die reine und angewandte Mathematik„Äč (ŽŹÖžĚľžĖī) 1874 (78): 46‚Äď62. doi :10.1515/crll.1874.78.46 . ISSN 0075-4102 . JFM 06.0116.01 . ‚ÜĎ ÍįÄ Žāė Stieltjes, T. J. (1905). „Äą79. Stieltjes a Hermite. Paris, 11 juillet 1885„ÄČ . B. Baillaud, H. Bourget. „ÄäCorrespondance d‚ÄôHermite et Stieltjes„Äč (ŪĒĄŽěϞ䧞Ėī). ŪĆĆŽ¶¨ : Gauthier-Villars. 160‚Äď164ž™Ĺ. ‚ÜĎ Mertens, F. (1897). ‚ÄúUeber eine zahlentheoretische Function‚ÄĚ. „ÄäSitzungsberichte der Kaiserlichen Akademie der Wissenschaften, Mathematisch-Naturwissenschaftliche Klasse, Abteilung 2a„Äč (ŽŹÖžĚľžĖī) 106 : 761‚Äď830. JFM 28.0177.01 .












![{\displaystyle \mu (n)=(-1)^{\sum _{p}n_{p}}\prod _{p}[n_{p}\leq 1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/625c61c055ae01d9a29facf78a0260009c96333f)
![{\displaystyle [\cdots ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51cc669ab2e6cf8641bcb1c0fa1c283d463b21e4)