표준 편차

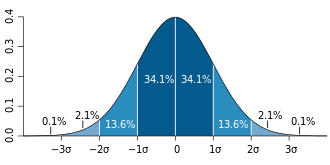
표준 편차(標準 偏差, 영어: standard deviation, SD)는 통계집단의 분산의 정도 또는 자료의 산포도를 나타내는 수치로, 분산의 음이 아닌 제곱근 즉, 분산을 제곱근한 것으로 정의된다. 표준편차가 작을수록 평균값에서 변량들의 거리가 가깝다.^[1] 통계학과 확률에서 주로 확률의 분포, 확률변수 혹은 측정된 인구나 중복집합에 적용된다. 관례에 따라 모집단은 그리스 문자로, 표본은 영어 알파벳으로 표기하는데, 모집단의 표준편차는 ${\displaystyle \sigma }$(시그마)로, 표본의 표준편차는 ${\displaystyle s}$(에스)로 나타낸다.^[2]

편차(deviation)는 관측값에서 평균 또는 중앙값을 뺀 것이다.

분산(variance)은 관측값에서 평균을 뺀 값을 제곱하고, 그것을 모두 더한 후 전체 개수로 나눠서 구한다. 즉, 차잇값의 제곱의 평균이다. 관측값에서 평균을 뺀 값인 편차를 모두 더하면 ${\displaystyle 0}$이 나오므로 제곱해서 더한다.

표준편차(standard deviation)는 분산을 제곱근한 것이다. 편차들(deviations)의 제곱합(SS, sum of square)에서 얻어진 값의 평균치인 분산의 성질로부터 다시 제곱근해서 원래 단위로 만들어줌으로써 얻게된다.

모표준편차(population standard deviation) ${\displaystyle \sigma }$는 모집단의 표준편차이다. 모분산 ${\displaystyle \sigma ^{2}}$에 제곱근을 씌워서 구한다.

표본표준편차(sample standard deviation) ${\displaystyle s}$는 표본의 표준편차이다. 표본분산 ${\displaystyle s^{2}}$에 제곱근을 씌워서 구한다.

확률변수 ${\displaystyle X}$의 기댓값 ${\displaystyle \operatorname {E} (X)}$를 ${\displaystyle \mu }$라 하자. 이 때 모집단 ${\displaystyle X}$의 표준편차 ${\displaystyle \sigma _{X}}$는 다음과 같이 정의한다.^[3]

${\displaystyle {\begin{aligned}\sigma &={\sqrt {\operatorname {E} \left((X-\mu )^{2}\right)}}\\&={\sqrt {\operatorname {E} \left(X^{2}\right)+\operatorname {E} (-2\mu X)+\operatorname {E} \left(\mu ^{2}\right)}}\\&={\sqrt {\operatorname {E} \left(X^{2}\right)-2\mu \operatorname {E} (X)+\mu ^{2}}}\\&={\sqrt {\operatorname {E} \left(X^{2}\right)-2\mu ^{2}+\mu ^{2}}}\\&={\sqrt {\operatorname {E} \left(X^{2}\right)-\mu ^{2}}}\\&={\sqrt {\operatorname {E} \left(X^{2}\right)-(\operatorname {E} (X))^{2}}}\end{aligned}}}$

유도과정에서 기댓값의 성질이 사용되었다. 표준편차는 분산의 제곱근과 같은 의미를 가진다.

경중률이 동일한 경우 표본 내의 어떤 변인 ${\displaystyle x}$가 가지는 모집단에서 표본(sample)의 표준편차의 추정치 ${\displaystyle s}$는 다음과 같다.

${\displaystyle s=\pm {\sqrt {\frac {\sum (x-{\overline {x}})^{2}}{n-1}}}=\pm {\sqrt {\frac {\sum \nu ^{2}}{n-1}}}}$

${\displaystyle s}$: 표본의 표준편차

${\displaystyle x}$: 변인

${\displaystyle {\overline {x}}}$: 표본의 평균

${\displaystyle n}$: 표본의 크기

${\displaystyle \nu }$: 잔차

분모를 ${\displaystyle n-1}$로 나누는 이유는 분산을 계산할 때 모평균이 아닌 표본평균을 사용했기 때문에 모집단의 편의 추정량(biased estimator)이 되므로, 분산이 불편 추정량(unbiased estimator)이 되도록 하기 위해서이다.^[4] ${\displaystyle n-1}$을 자유도(degree of freedom)라고 본다.^[5]

경중률을 ${\displaystyle w}$라 할 때, ${\displaystyle \sum w=n}$인 경우에는 표본표준편차 ${\displaystyle s}$를 다음과 같이 구한다.^[4]

${\displaystyle s=\pm {\sqrt {\frac {\sum w(x-{\overline {x}})^{2}}{n-1}}}=\pm {\sqrt {\frac {\sum w\nu ^{2}}{n-1}}}}$

위키미디어 공용에 표준 편차 주제와 관련된 미디어 분류가 있습니다.

• 편차
• 표준 점수
• 평균편차
• 68-95-99.7 규칙(경험적인 규칙)
• 표준오차
• 절대편차
• 공분산
• 변이 가설 (variability hypothesis)
• 분산

이 글은 통계학에 관한 토막글입니다. 여러분의 지식으로 알차게 문서를 완성해 갑시다.