Елемент (математика)

Елемент или член — некоја единица или предмет од каквишто се состои едно множество.

Ако запишеме A = {1, 2, 3, 4 }, ова значи дека елементите на множеството A се броевите 1, 2, 3 и 4. Множествата од елементи на A, на пр. {1, 2} се подмножества на A.

Самите множества можат да бидат елементи. На пример, имаме множество B = {1, 2, {3, 4}}. Елементите на B не се 1, 2, 3 и  4, туку B има само три елемента: 1, 2 и множеството {3, 4}.

Елемент на едно множество може да биде било што. На пример, C = { црвена, зелена, сина } е множеството чиишто елементи се боите црвена, зелена и сина. Множеството без ниеден елемент се нарекува празно множество (се запишува со „{}“ или „${\displaystyle \varnothing }$“).^[1]

Релацијата „е елемент на“ се нарекува и членство во множество и се означува со симболот  ∈. Запишувајќи вака:

${\displaystyle x\in A\,}$

велиме дека „x е елемент на A“. Истоветни изрази се: „x е член на A“, „x припаѓа на A“, „${\displaystyle x}$ е во A“ и „x лежи во A“. Во употреба се и изразите „A го содржи x“ и „A го вклучува x“, но некои автори ги користат со значење „x е подмножество на A“.^[2]

Наредбата за овој симбол во означувачкиот јазик LaTeX е „\in“.

Негацијата на членството во едно множество се означува со ∉.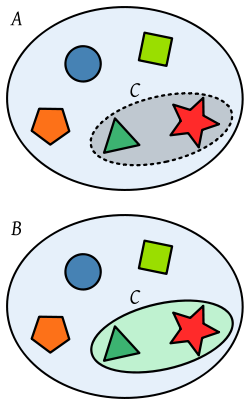

Бројот на елементи во дадено множество е својство наречено кардиналност (неформално речено, големина на множеството). Во горенаведениве примери, кардиналноста на множеството A изнесува 4, додека кардиналноста на множеството B и множеството C изнесува 3. Бесконечно множество е множество со бесконечен број на елементи, додека конечното множество има извесен (конечен) број на елементи. Горенаведените множества се примери за конечни множества. Пример за бесконечно множество е множеството на природни броеви, N = { 1, 2, 3, 4, ...}.

Земајќи ги гореопределените множества:

• 2 ∈ A
• {3,4} ∈ B
• {3,4} е член на B
• жолта ∉ C
• Кардиналноста на D = { 2, 4,  8, 10, 12 } е конечна и еднаква на 5.
• Кардиналноста на P = { 2, 3, 5, 7, 11, 13, ...} (простите броеви) е бесконечна, како што докажал Евклид.

• Paul R. Halmos 1960, Naive Set Theory, Springer-Verlag, NY, ISBN 0-387-90092-6.
• Patrick Suppes 1960, 1972, Axiomatic Set Theory, Dover Publications, Inc. NY, ISBN 0-486-61630-4.