–ě–Ņ–ł—Ā–Ĺ–į —Ā—ā–į—ā–ł—Ā—ā–ł–ļ–į - –Ę–ł–Ņ–ĺ–≤–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł–Ē. –Ę–ł–Ņ–ĺ–≤–ł –Ĺ–į –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł –ł –Ĺ–ł–≤–Ĺ–ĺ –≥—Ä—É–Ņ–ł—Ä–į—ö–Ķ–ė–ľ–į —á–Ķ—ā–ł—Ä–ł —ā—Ä–ł–Ņ–ĺ–≤–ł –Ĺ–į –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł1.
–Ě–ĺ–ľ–ł–Ĺ–į–Ľ–Ĺ–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł–Ę—É–ļ–į –ĺ–Ī–Ķ–Ľ–Ķ–∂–ł—ė–Ķ—ā–ĺ –Ķ —á–ł—Ā—ā–ĺ –ļ–≤–į–Ľ–ł—ā–į—ā–ł–≤–Ĺ–ĺ. –ú–ĺ–∂–Ĺ–ł—ā–Ķ –ł—Ā—Ö–ĺ–ī–ł —Ā–Ķ –∑–Ī–ĺ—Ä–ĺ–≤–ł-–ł–ľ–ł—ö–į –ł –ł—Ā—ā–ł—ā–Ķ —Ā–Ķ —Ā–į–ľ–ł—ā–Ķ –ļ–į—ā–Ķ–≥–ĺ—Ä–ł–ł, –ĺ–ī–Ĺ–ĺ—Ā–Ĺ–ĺ –ļ–Ľ–į—Ā–ł –Ņ—Ä–ł –≥—Ä—É–Ņ–ł—Ä–į—ö–Ķ. –°–ĺ –≤–į–ļ–≤–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł –Ĺ–Ķ –ľ–ĺ–∂–Ķ–ľ–Ķ –ī–į –Ņ—Ä–į–≤–ł–ľ–Ķ –Ĺ–ł–ļ–į–ļ–≤–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—á–ļ–ł –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł. –í–į–∂–Ĺ–ĺ: –Ě–ĺ–ľ–ł–Ĺ–į–Ľ–Ĺ–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł —Ā–Ķ–ļ–ĺ–≥–į—ą —Ā–Ķ –≥—Ä—É–Ņ–ł—Ä–į–į—ā.
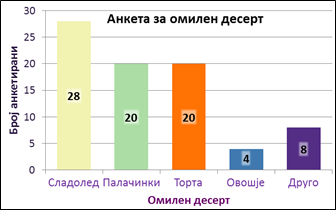
–ü—Ä–ł–ľ–Ķ—Ä –Ē-1: –ź–Ĺ–ļ–Ķ—ā–ł—Ä–į–Ĺ–ł —Ā–Ķ 80 –Ľ—É—ď–Ķ –∑–į –Ĺ–ł–≤–Ĺ–ł–ĺ—ā –ĺ–ľ–ł–Ľ–Ķ–Ĺ –ī–Ķ—Ā–Ķ—Ä—ā (–≤–ł–ī–ł –Ę–į–Ī–Ķ–Ľ–į 17).
–Ę–į–Ī–Ķ–Ľ–į 17: –†–Ķ–∑—É–Ľ—ā–į—ā–ł –ĺ–ī –į–Ĺ–ļ–Ķ—ā–į –†–Ķ—ą–Ķ–Ĺ–ł–Ķ: –ě–Ī–Ķ–Ľ–Ķ–∂—ė–Ķ—ā–ĺ –Ķ ‚Äě–ĺ–ľ–ł–Ľ–Ķ–Ĺ –ī–Ķ—Ā–Ķ—Ä—ā‚Äú –ł –ľ–ĺ–∂–Ĺ–ł—ā–Ķ –ł—Ā—Ö–ĺ–ī–ł —ā—É–ļ–į —Ā–Ķ {–°, –ü, –Ę, –ě, –Ē}, –ĺ–ī–Ĺ–ĺ—Ā–Ĺ–ĺ {–°–Ľ–į–ī–ĺ–Ľ–Ķ–ī, –ü–į–Ľ–į—á–ł–Ĺ–ļ–ł, –Ę–ĺ—Ä—ā–į, –ě–≤–ĺ—ą—ė–Ķ, –Ē—Ä—É–≥–ĺ}. –ą–į—Ā–Ĺ–ĺ –Ķ –ī–Ķ–ļ–į —Ā–Ķ –ł–ľ–ł—ö–į. –Ę–ł–Ķ —Ā–Ķ –ł —Ā–į–ľ–ł—ā–Ķ –ļ–Ľ–į—Ā–ł –Ņ—Ä–ł –≥—Ä—É–Ņ–ł—Ä–į—ö–Ķ. –ó–Ĺ–į—á–ł, –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł—ā–Ķ —Ā–Ķ –Ĺ–ĺ–ľ–ł–Ĺ–į–Ľ–Ĺ–ł –ł —ā—Ä–Ķ–Ī–į –ī–į —Ā–Ķ –≥—Ä—É–Ņ–ł—Ä–į–į—ā –Ņ–ĺ –ļ–Ľ–į—Ā–ł = –ł–ľ–ł—ö–į –Ĺ–į –ī–Ķ—Ā–Ķ—Ä—ā. –ą–į –Ĺ–į—ė–ī–Ķ–ľ–Ķ —á–Ķ—Ā—ā–ĺ—ā–į—ā–į –Ĺ–į —Ā–Ķ–ļ–ĺ—ė —ā–ł–Ņ –Ĺ–į –ī–Ķ—Ā–Ķ—Ä—ā (–Ņ—Ä–ĺ–≤–Ķ—Ä—É–≤–į—ė—ú–ł –ī–Ķ–ļ–į —á–Ķ—Ā—ā–ĺ—ā–ł—ā–Ķ —Ā–Ķ —Ā–ĺ–Ī–ł—Ä–į–į—ā –ī–ĺ N=80). –í–ĺ –Ę–į–Ī–Ķ–Ľ–į 18 –Ķ —Ā–ĺ–ĺ–ī–≤–Ķ—ā–Ĺ–į—ā–į —á–Ķ—Ā—ā–ĺ—ā–Ĺ–į —ā–į–Ī–Ķ–Ľ–į.
–Ę–į–Ī–Ķ–Ľ–į 18: –Ě–ĺ–ľ–ł–Ĺ–į–Ľ–Ĺ–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł ‚Äď –ĺ—Ä–≥–į–Ĺ–ł–∑–ł—Ä–į–Ĺ–ł –∑–į –ĺ–Ī—Ä–į–Ī–ĺ—ā–ļ–į –≤–ĺ —á–Ķ—Ā—ā–ĺ—ā–Ĺ–į —ā–į–Ī–Ķ–Ľ–į –ď–ł –Ņ—Ä–Ķ—ā—Ā—ā–į–≤–ł–ľ–Ķ –ĺ–≤–ł–Ķ –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł —Ā–ĺ —Ā—ā–ĺ–Ľ–Ī–Ķ—Ā—ā –ī–ł—ė–į–≥—Ä–į–ľ (–≤–ł–ī–ł –°–Ľ–ł–ļ–į 13).
–ö–Ľ–į—Ā–ł—ā–Ķ —ā—É–ļ–į —Ā–Ķ –ł–ľ–ł—ö–į –ł –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–ļ–ł –ī–į —Ā–Ķ —Ä–į–Ī–ĺ—ā–į—ā –Ĺ–ł—ą—ā–ĺ —Ā–ĺ –Ĺ–ł–≤. –ú–Ķ—ď—É—ā–ĺ–į, —á–Ķ—Ā—ā–ĺ—ā–ł—ā–Ķ —Ā–Ķ –Ī—Ä–ĺ–Ķ–≤–ł –ł –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ņ—Ä–Ķ—Ā–ľ–Ķ—ā–į –Ņ—Ä–ĺ—Ü–Ķ–Ĺ—ā–ĺ—ā –ļ–ĺ—ė –Ņ—Ä–ł–Ņ–į—ď–į –≤–ĺ —Ā–Ķ–ļ–ĺ—ė–į –ļ–Ľ–į—Ā–į, –ĺ–ī–Ĺ–ĺ—Ā–Ĺ–ĺ –ī–į —Ā–Ķ –Ņ—Ä–Ķ–ľ–Ķ—ā–į—ā —ā.–Ĺ. —Ä–Ķ–Ľ–į—ā–ł–≤–Ĺ–ł —á–Ķ—Ā—ā–ĺ—ā–ł. –†–Ķ–Ľ–į—ā–ł–≤–Ĺ–į —á–Ķ—Ā—ā–ĺ—ā–į = –Ņ—Ä–ĺ—Ü–Ķ–Ĺ—ā = f/N–ą–į –ī–Ķ–Ľ–ł–ľ–Ķ —á–Ķ—Ā—ā–ĺ—ā–į—ā–į —Ā–ĺ –≤–ļ—É–Ņ–Ĺ–ł–ĺ—ā –Ī—Ä–ĺ—ė –Ĺ–į —á–Ķ—Ā—ā–ĺ—ā–ł—ā–Ķ, —ā.–Ķ. —Ā–ĺ –≥–ĺ–Ľ–Ķ–ľ–ł–Ĺ–į—ā–į –Ĺ–į –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł N. –ü–ĺ—ā–ĺ–į, –ĺ–≤–ĺ—ė —Ä–Ķ–∑—É–Ľ—ā–į—ā –≥–ĺ –Ņ–ĺ–ľ–Ĺ–ĺ–∂–ł–ľ–Ķ —Ā–ĺ 100% –∑–į –ī–į –ī–ĺ–Ī–ł–ľ–Ķ –Ņ—Ä–ĺ—Ü–Ķ–Ĺ—ā. –í–ĺ –Ņ—Ä–ł–ľ–Ķ—Ä –Ē-1, –≤–ļ—É–Ņ–Ĺ–ł–ĺ—ā –Ī—Ä–ĺ—ė –Ĺ–į —á–Ķ—Ā—ā–ĺ—ā–ł—ā–Ķ –Ķ N=80. –ą–į –ī–Ķ–Ľ–ł–ľ–Ķ —Ā–Ķ–ļ–ĺ—ė–į —á–Ķ—Ā—ā–ĺ—ā–į —Ā–ĺ N=80 –∑–į –ī–į —ė–į –ī–ĺ–Ī–ł–Ķ–ľ–Ķ —Ä–Ķ–Ľ–į—ā–ł–≤–Ĺ–į —á–Ķ—Ā—ā–ĺ—ā–Ĺ–į —ā–į–Ī–Ķ–Ľ–į (–≤–ł–ī–ł –Ę–į–Ī–Ķ–Ľ–į 19 ).
–Ę–į–Ī–Ķ–Ľ–į 19: –†–Ķ–Ľ–į—ā–ł–≤–Ĺ–į —á–Ķ—Ā—ā–ĺ—ā–Ĺ–į —ā–į–Ī–Ķ–Ľ–į –†–Ķ–Ľ–į—ā–ł–≤–Ĺ–į —á–Ķ—Ā—ā–ĺ—ā–Ĺ–į —ā–į–Ī–Ķ–Ľ–į –ľ–ĺ–∂–Ķ –≥—Ä–į—Ą–ł—á–ļ–ł –ī–į —Ā–Ķ –Ņ—Ä–Ķ—ā—Ā—ā–į–≤–ł —Ā–ĺ —Ā—ā–ĺ–Ľ–Ī–Ķ—Ā—ā –ł–Ľ–ł —Ā–ĺ —Ā–Ķ–ļ—ā–ĺ—Ä—Ā–ļ–ł –ī–ł—ė–į–≥—Ä–į–ľ –ļ–į–ļ–ĺ –≤–ĺ –°–Ľ–ł–ļ–į 16 –ł –°–Ľ–ł–ļ–į 17. –ó–į–Ī–Ķ–Ľ–Ķ–∂–Ķ—ā–Ķ –≥–ł —Ä–į–∑–Ľ–ł–ļ–ł—ā–Ķ –Ņ–ĺ–ľ–Ķ—ď—É –ī–≤–į—ā–į —Ā—ā–ĺ–Ľ–Ī–Ķ—Ā—ā –ī–ł—ė–į–≥—Ä–į–ľ–ł –°–Ľ–ł–ļ–į 13 –ł –°–Ľ–ł–ļ–į 16. –°–Ķ–ļ—ā–ĺ—Ä—Ā–ļ–ł –ī–ł—ė–į–≥—Ä–į–ľ —Ā–Ķ–ļ–ĺ–≥–į—ą –Ķ —Ä–Ķ–Ľ–į—ā–ł–≤–Ĺ–į!
–ě—Ä–ī–ł–Ĺ–į–Ľ–Ĺ–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł–ö–į–ļ–ĺ –ļ–į—ė –Ĺ–ĺ–ľ–ł–Ĺ–į–Ľ–Ĺ–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł, –ĺ–Ī–Ķ–Ľ–Ķ–∂–ł—ė–Ķ—ā–ĺ –Ĺ–į –ĺ—Ä–ī–ł–Ĺ–į–Ľ–Ĺ–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł –Ķ —á–ł—Ā—ā–ĺ –ļ–≤–į–Ľ–ł—ā–į—ā–ł–≤–Ĺ–ĺ, –Ĺ–ĺ —Ā–Ķ –Ī—Ä–ĺ–Ķ–≤–ł-–ł–ľ–ł—ö–į. –Ě–į –Ņ—Ä–ł–ľ–Ķ—Ä ‚Äě–Ī—Ä–ĺ—ė –Ĺ–į —á–Ķ–≤–Ķ–Ľ‚Äú –ł–Ľ–ł ‚Äě–≥–ĺ–ī–ł–Ĺ–į –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī—Ā—ā–≤–ĺ‚Äú —Ā–Ķ –ĺ—Ä–ī–ł–Ĺ–į–Ľ–Ĺ–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł. –Ě–Ķ–ľ–į —Ā–ľ–ł—Ā–Ľ–į –ī–į —Ā–Ķ –Ņ—Ä–į–≤–ł –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į —Ā–ĺ –Ĺ–ł–≤. –ú–Ķ—ď—É—ā–ĺ–į, –ļ–į—ė –≤–į–ļ–≤–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł –Ņ—Ä–ł—Ä–ĺ–ī–Ĺ–ĺ –Ķ –ļ–Ľ–į—Ā–ł—ā–Ķ –ī–į —Ā–Ķ –Ņ–ĺ–ī—Ä–Ķ–ī–į—ā –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ł –Ņ–ĺ –Ĺ–ł–≤–Ĺ–į—ā–į –≤—Ä–Ķ–ī–Ĺ–ĺ—Ā—ā. –°–ĺ –ĺ–≤–į –ĺ—Ä–ī–ł–Ĺ–į–Ľ–Ĺ–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł —Ā–Ķ —Ä–į–∑–Ľ–ł–ļ—É–≤–į–į—ā –ĺ–ī ‚Äě—á–ł—Ā—ā–ł‚Äú –Ĺ–ĺ–ľ–ł–Ĺ–į–Ľ–Ĺ–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł, –ļ–į–ī–Ķ —ą—ā–ĺ —Ä–Ķ–ī–ĺ—Ā–Ľ–Ķ–ī–ĺ—ā –Ĺ–į –ļ–Ľ–į—Ā–ł—ā–Ķ –Ķ –Ĺ–į—ą–ł–ĺ—ā –ł–∑–Ī–ĺ—Ä. –ú–Ķ—ď—É—ā–ĺ–į, —ā–ĺ–į –Ķ –Ķ–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–į—ā–į —Ä–į–∑–Ľ–ł–ļ–į. –Ě–į –ł—Ā—ā–ł–ĺ—ā –Ĺ–į—á–ł–Ĺ —Ā–Ķ –ĺ–Ī—Ä–į–Ī–ĺ—ā—É–≤–į–į—ā, —ā.–Ķ. —Ā–ĺ –≥—Ä—É–Ņ–ł—Ä–į—ö–Ķ —Ā–ĺ —á–Ķ—Ā—ā–ĺ—ā–ł –ł–Ľ–ł —Ä–Ķ–Ľ–į—ā–ł–≤–Ĺ–ł —á–Ķ—Ā—ā–ĺ—ā–ł –ł —Ā–ĺ –ł—Ā—ā–ł –ī–ł—ė–į–≥—Ä–į–ľ–ł –≥—Ä–į—Ą–ł—á–ļ–ł —Ā–Ķ –Ņ—Ä–Ķ—ā—Ā—ā–į–≤—É–≤–į–į—ā (—Ā—ā–ĺ–Ľ–Ī–Ķ—Ā—ā –ł —Ā–Ķ–ļ—ā–ĺ—Ä—Ā–ļ–ł). –í–į–∂–Ĺ–ĺ: –ě—Ä–ī–ł–Ĺ–į–Ľ–Ĺ–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł —Ā–Ķ–ļ–ĺ–≥–į—ą —Ā–Ķ –≥—Ä—É–Ņ–ł—Ä–į–į—ā.
–ü—Ä–ł–ľ–Ķ—Ä –Ē-2: –Ě–į –ī–Ķ–Ĺ 20.02.2002 –≤–ĺ –Ķ–ī–Ĺ–į —Ą–į–Ī—Ä–ł–ļ–į –∑–į —á–Ķ–≤–Ľ–ł, –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –Ņ–į—Ä–ĺ–≤–ł –Ĺ–į –ľ–į—ą–ļ–ł —á–Ķ–≤–Ľ–ł –Ķ –ĺ–Ņ–ł—ą–į–Ĺ–ĺ –≤–ĺ –Ę–į–Ī–Ķ–Ľ–į 20. –Ē–į —Ā–Ķ –Ĺ–į–Ņ—Ä–į–≤–ł —Ā–ĺ–ĺ–ī–≤–Ķ—ā–Ĺ–į —Ä–Ķ–Ľ–į—ā–ł–≤–Ĺ–į —á–Ķ—Ā—ā–ĺ—ā–Ĺ–į —ā–į–Ī–Ķ–Ľ–į –ł —Ā–ĺ–ĺ–ī–≤–Ķ—ā–Ĺ–ł —Ā—ā–ĺ–Ľ–Ī–Ķ—Ā—ā –ī–ł—ė–į–≥—Ä–į–ľ–ł –∑–į –ī–į–ī–Ķ–Ĺ–į—ā–į –ł –Ĺ–į–Ņ—Ä–į–≤–Ķ–Ĺ–į—ā–į —ā–į–Ī–Ķ–Ľ–į.
–Ę–į–Ī–Ķ–Ľ–į 20: –ď—Ä—É–Ņ–ł—Ä–į–Ĺ–ł –ĺ—Ä–ī–ł–Ĺ–į–Ľ–Ĺ–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł –†–Ķ—ą–Ķ–Ĺ–ł–Ķ: –ě–Ī–Ķ–Ľ–Ķ–∂—ė–Ķ—ā–ĺ –Ķ ‚Äě–Ī—Ä–ĺ—ė –Ĺ–į —á–Ķ–≤–Ķ–Ľ‚Äú, –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł —Ā–Ķ –Ī—Ä–ĺ–Ķ–≤–ł –ł –ľ–ĺ–∂–Ĺ–ł—ā–Ķ –ł—Ā—Ö–ĺ–ī–ł, –ĺ–ī–Ĺ–ĺ—Ā–Ĺ–ĺ –ļ–Ľ–į—Ā–ł—ā–Ķ —Ā–Ķ {40,41,42,43,44,45,46,47}. –ü–ĺ–ī–į—ā–ĺ—Ü–ł—ā–Ķ —Ā–Ķ –ĺ–ī —ā–ł–Ņ –ĺ—Ä–ī–ł–Ĺ–į–Ľ–Ĺ–ł, —ā.–Ķ. –ł–ľ–į —Ā–ľ–ł—Ā–Ľ–į –ī–į –≥–ł —Ä–Ķ–ī–ł–ľ–Ķ –ļ–Ľ–į—Ā–ł—ā–Ķ –Ņ–ĺ –Ī—Ä–ĺ—ė –Ĺ–į —á–Ķ–≤–Ķ–Ľ, –Ĺ–ĺ –Ĺ–Ķ–ľ–į —Ā–ľ–ł—Ā–Ľ–į –ī–į —Ā–Ķ —Ā–ĺ–Ī–ł—Ä–į–į—ā –ī–≤–į –Ī—Ä–ĺ–Ķ–≤–ł –Ĺ–į —á–Ķ–≤–Ľ–ł –ł–Ľ–ł –ī–į —Ā–Ķ –Ī–į—Ä–į –Ĺ–ł–≤–Ĺ–į –į—Ä–ł—ā–ľ–Ķ—ā–ł—á–ļ–į —Ā—Ä–Ķ–ī–ł–Ĺ–į. –ď—Ä–į—Ą–ł—á–ļ–ĺ –Ņ—Ä–Ķ—ā—Ā—ā–į–≤—É–≤–į—ö–Ķ –Ķ —Ā–ĺ —Ā—ā–ĺ–Ľ–Ī–Ķ—Ā—ā –ī–ł—ė–į–≥—Ä–į–ľ. –ú–ĺ–∂–Ķ–≤–ľ–Ķ –ł —Ā–Ķ–ļ—ā–ĺ—Ä—Ā–ļ–ł, –Ĺ–ĺ –ľ–Ĺ–ĺ–≥—É —Ā–Ķ–ļ—ā–ĺ—Ä–ł —ú–Ķ –Ī–ł–ī–į—ā –ł –Ĺ–Ķ–ľ–į –ī–į –Ī–ł–ī–Ķ –ľ–Ĺ–ĺ–≥—É –Ņ—Ä–Ķ–≥–Ľ–Ķ–ī–Ĺ–ĺ. –ó–į—ā–ĺ–į, –ī–į–≤–į–ľ–Ķ —Ā—ā–į–Ĺ–ī–į—Ä–ī–Ķ–Ĺ —Ā—ā–ĺ–Ľ–Ī–Ķ—Ā—ā –ī–ł—ė–į–≥—Ä–į–ľ (–°–Ľ–ł–ļ–į 16 ) —Ā–ĺ –į–Ņ—Ā–ĺ–Ľ—É—ā–Ĺ–ł—ā–Ķ —á–Ķ—Ā—ā–ĺ—ā–ł (–Ī—Ä–ĺ—ė –Ņ–į—Ä–ĺ–≤–ł) –ł —Ä–Ķ–Ľ–į—ā–ł–≤–Ķ–Ĺ —Ā—ā–ĺ–Ľ–Ī–Ķ—Ā—ā –ī–ł—ė–į–≥—Ä–į–ľ (–°–Ľ–ł–ļ–į 17) —Ā–ĺ —Ä–Ķ–Ľ–į—ā–ł–≤–Ĺ–ł —á–Ķ—Ā—ā–ĺ—ā–ł (–Ņ—Ä–ĺ—Ü–Ķ–Ĺ—ā–ł).
–ö–ĺ–ľ–Ķ–Ĺ—ā–į—Ä –ĺ–ī —Ā—ā–į—ā–ł—Ā—ā–ł–ļ–į—ā–į: –ó–į–Ī–Ķ–Ľ–Ķ–∂–Ķ—ā–Ķ –ī–Ķ–ļ–į –≤–ĺ —Ä–Ķ–Ľ–į—ā–ł–≤–Ĺ–Ķ–Ĺ —Ā—ā–ĺ–Ľ–Ī–Ķ—Ā—ā –ī–ł—ė–į–≥—Ä–į–ľ –Ĺ–Ķ —Ā–Ķ –∑–Ĺ–į–Ķ –ļ–ĺ–Ľ–ļ—É –Ķ –≥–ĺ–Ľ–Ķ–ľ–ł–Ĺ–į—ā–į –Ĺ–į –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł—ā–Ķ N, —ā.–Ķ. –≤–ĺ –ĺ–≤–ĺ—ė –Ņ—Ä–ł–ľ–Ķ—Ä –Ĺ–Ķ —Ā–Ķ –∑–Ĺ–į–Ķ –ļ–ĺ–Ľ–ļ—É –Ņ–į—Ä–ĺ–≤–ł –Ī–ł–Ľ–Ķ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ķ–Ĺ–ł.
–Ď—Ä–ĺ—ė–Ĺ–ł-–ļ–Ľ–į—Ā–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł–ö–į–ļ–ĺ –Ņ—Ä–ł–ľ–Ķ—Ä –∑–į –Ī—Ä–ĺ—ė–Ĺ–ł-–ļ–Ľ–į—Ā–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł —Ā–Ķ —É—á–Ķ–Ĺ–ł—á–ļ–ł –ĺ—Ü–Ķ–Ĺ–ļ–ł (–≤–ł–ī–ł –Ņ–ĺ–ī–ĺ–Ľ—É –Ņ—Ä–ł–ľ–Ķ—Ä –Ē-3). –Ę—É–ļ–į –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł—ā–Ķ –ł–ľ–į–į—ā –ī–≤–Ķ –≤–į–∂–Ĺ–ł –ĺ—Ā–ĺ–Ī–ł–Ĺ–ł:
–°–ĺ —ā–ĺ–į —Ā–į–ľ–ł—ā–Ķ –Ī—Ä–ĺ–Ķ–≤–ł —Ā–Ķ —Ā–ľ–Ķ—ā–į–į—ā –∑–į –ļ–Ľ–į—Ā–ł –Ņ—Ä–ł –≥—Ä—É–Ņ–ł—Ä–į—ö–Ķ.
–ü—Ä–ł–ľ–Ķ—Ä –Ē-3: –ě—Ü–Ķ–Ĺ–ļ–ł—ā–Ķ –Ņ–ĺ –ł—Ā—ā–ĺ—Ä–ł—ė–į –Ĺ–į 35 —É—á–Ķ–Ĺ–ł—Ü–ł –≤–ĺ –Ķ–ī–Ķ–Ĺ –ļ–Ľ–į—Ā —Ā–Ķ –ī–į–ī–Ķ–Ĺ–ł –≤–ĺ –Ę–į–Ī–Ķ–Ľ–į 21. –ó–į –ł—Ā—ā–ł—ā–Ķ –ī–į —Ā–Ķ –Ĺ–į–Ņ—Ä–į–≤–ł —Ā–ĺ–ĺ–ī–≤–Ķ—ā–Ķ–Ĺ –ī–ł—ė–į–≥—Ä–į–ľ.
–Ę–į–Ī–Ķ–Ľ–į 21: –°—É—Ä–ĺ–≤–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł –ĺ–ī —ā–ł–Ņ –Ī—Ä–ĺ—ė–Ĺ–ł-–ļ–Ľ–į—Ā–ł –†–Ķ—ą–Ķ–Ĺ–ł–Ķ: –ě–Ī–Ķ–Ľ–Ķ–∂–ł—ė–Ķ—ā–ĺ –Ķ –ĺ—Ü–Ķ–Ĺ–ļ–į, –į –ľ–ĺ–∂–Ĺ–ł—ā–Ķ –ł—Ā—Ö–ĺ–ī–ł —Ā–Ķ: { 1, 2, 3, 4, 5}.
–ą–į—Ā–Ĺ–ĺ –Ķ –ī–Ķ–ļ–į —á–Ķ—Ā—ā–ĺ—ā–ł—ā–Ķ —Ā–Ķ –Ī–į—Ä–į—ā –Ī—Ä–ĺ–Ķ—ė—ú–ł ‚Äě–ö–ĺ–Ľ–ļ—É 5-–ļ–ł?‚Äú, ‚Äě–ö–ĺ–Ľ–ļ—É 4-–ļ–ł?‚Äú,... . –ó–Ĺ–į—á–ł –Ī—Ä–ĺ–Ķ–≤–ł—ā–Ķ —Ā–Ķ —Ā–į–ľ–ł—ā–Ķ –ļ–Ľ–į—Ā–ł (–≤–ł–ī–ł –Ę–į–Ī–Ķ–Ľ–į 22 –ł –Ę–į–Ī–Ķ–Ľ–į 23 ).
–Ę–į–Ī–Ķ–Ľ–į 22: –ď—Ä—É–Ņ–ł—Ä–į–Ĺ–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł –Ņ–ĺ –Ī—Ä–ĺ—ė–Ĺ–į-–ļ–Ľ–į—Ā–į
–Ę–į–Ī–Ķ–Ľ–į 23: –°–ĺ–ĺ–ī–≤–Ķ—ā–Ĺ–į —á–Ķ—Ā—ā–ĺ—ā–Ĺ–į —ā–į–Ī–Ķ–Ľ–į –ě–ī –ī—Ä—É–≥–į —Ā—ā—Ä–į–Ĺ–į, –ļ–Ľ–į—Ā–ł—ā–Ķ —Ā–Ķ –Ī—Ä–ĺ–Ķ–≤–ł –ł –ł–ľ–į —Ā–ľ–ł—Ā–Ľ–į –ī–į —Ā–Ķ –Ņ—Ä–į–≤–į—ā –ĺ–ī—Ä–Ķ–ī–Ķ–Ĺ–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—á–ļ–ł –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł —Ā–ĺ –Ĺ–ł–≤, —ā.–Ķ. –Ĺ–į –Ņ—Ä–ł–ľ–Ķ—Ä –ľ–ĺ–∂–Ķ–ľ–Ķ –ī–į –Ī–į—Ä–į–ľ–Ķ ‚Äě–Ņ—Ä–ĺ—Ā–Ķ—á–Ĺ–į—ā–į –ĺ—Ü–Ķ–Ĺ–ļ–į‚Äú. –í–į–ļ–≤–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł –ľ–ĺ–∂–į—ā –ī–į —Ā–Ķ –Ņ—Ä–Ķ—ā—Ā—ā–į–≤–į—ā —Ā–ĺ —Ā—ā–ĺ–Ľ–Ī–Ķ—Ā—ā –ī–ł—ė–į–≥—Ä–į–ľ (–≤–ł–ī–ł –°–Ľ–ł–ļ–į 18) –ł–Ľ–ł —Ā–ĺ —Ā–Ķ–ļ—ā–ĺ—Ä—Ā–ļ–ł –ī–ł—ė–į–≥—Ä–į–ľ (–≤–ł–ī–ł –°–Ľ–ł–ļ–į 19). –í–į–∂–Ĺ–ĺ: –°–ĺ –≥—Ä—É–Ņ–ł—Ä–į—ö–Ķ –Ĺ–į –Ĺ–ĺ–ľ–ł–Ĺ–į–Ľ–Ĺ–ł, –ĺ—Ä–ī–ł–Ĺ–į–Ľ–Ĺ–ł –ł–Ľ–ł –Ī—Ä–ĺ—ė–Ĺ–ł-–ļ–Ľ–į—Ā–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł, –Ĺ–ł–ļ–į–ļ–≤–ł –ł–Ĺ—Ą–ĺ—Ä–ľ–į—Ü–ł–ł –Ĺ–Ķ —Ā–Ķ –≥—É–Ī–į—ā. –ě–≤–į –Ĺ–Ķ –≤–į–∂–ł –Ņ—Ä–ł –Ī—Ä–ĺ—ė–Ĺ–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł!
–Ē–ł—ė–į–≥—Ä–į–ľ–ł —Ā–ĺ —Ā—ā–ĺ–Ľ–Ī–ĺ–≤–ł ‚Äď –°—ā–ĺ–Ľ–Ī–Ķ—Ā—ā –ī–ł—ė–į–≥—Ä–į–ľ –ł–Ľ–ł –•–ł—Ā—ā–ĺ–≥—Ä–į–ľ?
–Ď—Ä–ĺ—ė–Ĺ–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł–Ę—É–ļ–į –ľ–ĺ–∂–Ĺ–ł—ā–Ķ –ł—Ā—Ö–ĺ–ī–ł —Ā–Ķ —Ä–į–∑–Ĺ–ĺ-—Ä–į–∑–Ĺ–ł –Ī—Ä–ĺ–Ķ–≤–ł. –ě–≤–į –∑–Ĺ–į—á–ł –ī–Ķ–ļ–į –ł–ľ–į –Ņ–ĺ–≤–Ķ—ú–Ķ –ĺ–ī 10 –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł —Ā–ĺ –Ņ–ĺ–≤–Ķ—ú–Ķ –ĺ–ī 10 —Ä–į–∑–Ľ–ł—á–Ĺ–ł –≤—Ä–Ķ–ī–Ĺ–ĺ—Ā—ā–ł. –ú–ĺ–∂–į—ā –ī–į —Ā–Ķ –Ņ–ĺ–≤—ā–ĺ—Ä—É–≤–į–į—ā –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł—ā–Ķ, –Ĺ–ĺ –Ņ–ĺ–≤–Ķ—ú–Ķ—ā–ĺ —Ā–Ķ —Ä–į–∑–Ľ–ł—á–Ĺ–ł. –Ę–į–ļ–≤–ł –ĺ–Ī–ł—á–Ĺ–ĺ –≥–ł –Ņ—Ä–ĺ–≥–Ľ–į—Ā–ł–ľ–Ķ –∑–į –Ī—Ä–ĺ—ė–Ĺ–ł2, –į –Ĺ–Ķ –Ī—Ä–ĺ—ė–Ĺ–ł-–ļ–Ľ–į—Ā–ł, –Ī–ł–ī–Ķ—ė—ú–ł –≤–į–ļ–≤–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł –Ĺ–į—ė—á–Ķ—Ā—ā–ĺ —Ā–Ķ –≥—Ä—É–Ņ–ł—Ä–į–į—ā –≤–ĺ –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł. –£–Ņ–į—ā—Ā—ā–≤–ĺ –∑–į –≥—Ä—É–Ņ–ł—Ä–į—ö–Ķ –Ĺ–į –Ī—Ä–ĺ—ė–Ĺ–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł –≤–ĺ –Ķ–ī–Ĺ–į–ļ–≤–ĺ–ī–ĺ–Ľ–∂–Ĺ–ł –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł
–ó–į–Ī–Ķ–Ľ–Ķ—ą–ļ–ł:
–ü—Ä–ł–ľ–Ķ—Ä –Ē-4: –ď–Ķ–Ĺ–Ķ—Ä–ł—Ä–į–Ĺ–ł —Ā–Ķ 100 –Ī—Ä–ĺ–Ķ–≤–ł –Ņ–ĺ–ľ–Ķ—ď—É 0 –ł 1 –Ĺ–į —Ā–Ľ—É—á–į–Ķ–Ĺ –Ĺ–į—á–ł–Ĺ –≤–ĺ –ď–Ķ–ĺ–≥–Ķ–Ī—Ä–į —Ā–ĺ random() –ł –∑–į–ĺ–ļ—Ä—É–∂–Ķ–Ĺ–ł —Ā–Ķ –Ĺ–į —ā—Ä–ł –ī–Ķ—Ü–ł–ľ–į–Ľ–ł (–≤–ł–ī–ł –Ę–į–Ī–Ķ–Ľ–į 24). –ė—Ā—ā–ł—ā–Ķ –ī–į —Ā–Ķ –Ņ–ĺ–ī–Ķ–Ľ–į—ā –Ĺ–į 5 –ł –Ĺ–į 10 –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł –ł –ī–į —Ā–Ķ –ī–į–ī–į–į—ā —Ā–ĺ–ĺ–ī–≤–Ķ—ā–Ĺ–ł—ā–Ķ —Ö–ł—Ā—ā–ĺ–≥—Ä–į–ľ–ł.
–Ę–į–Ī–Ķ–Ľ–į 24 : –°—É—Ä–ĺ–≤–ł –Ī—Ä–ĺ—ė–Ĺ–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł –†–Ķ—ą–Ķ–Ĺ–ł–Ķ: –®—ā–ĺ –∑–į–Ī–Ķ–Ľ–Ķ–∂–ł–ľ–Ķ –≤–ĺ –ĺ–≤–ĺ—ė –Ņ—Ä–ł–ľ–Ķ—Ä?
–ď–Ľ–Ķ–ī–į—ė—ú–ł —ė–į —ā–ĺ—á–ļ–į 2 –Ņ–ĺ–≥–ĺ—Ä–Ķ, –Ī–ł —ā—Ä–Ķ–Ī–į–Ľ–ĺ –ī–į –Ĺ–ł –Ķ —ė–į—Ā–Ĺ–ĺ –ī–Ķ–ļ–į –Ĺ–į—ė–ī–ĺ–Ī—Ä–ĺ –Ķ –ī–į –≥–ĺ –≥–Ľ–Ķ–ī–į–ľ–Ķ –≥–Ľ–į–≤–Ĺ–ł–ĺ—ā –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ –ļ–į–ļ–ĺ [0,1], –į –Ĺ–Ķ [0.111, 0.993] –ł —ā–ĺ–į –∑–į –Ĺ–Ķ–ļ–ĺ–Ľ–ļ—É –Ņ—Ä–ł—á–ł–Ĺ–ł:
–ó–Ĺ–į—á–ł, –≥–Ľ–į–≤–Ĺ–ł–ĺ—ā –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ –≥–ĺ –∑–Ķ–ľ–Ķ–ľ–Ķ [0,1]. –í–ĺ –Ę–į–Ī–Ķ–Ľ–į 25 –ī–į–ī–Ķ–Ĺ–ł —Ā–Ķ –ī–≤–Ķ –≥—Ä—É–Ņ–ł—Ä–į—ö–į –Ķ–ī–Ĺ–į —Ā–ĺ n=5 –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł –ł –Ķ–ī–Ĺ–į —Ā–ĺ n=10 –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł –ļ–ĺ—Ä–ł—Ā—ā–Ķ—ė—ú–ł –≥–ĺ ‚Äě–Ľ–Ķ–≤–ł–ĺ—ā –ī–ĺ–≥–ĺ–≤–ĺ—Ä –∑–į –≥—Ä–į–Ĺ–ł—Ü–ł—ā–Ķ‚Äú (left endpoint convention).
–Ę–į–Ī–Ķ–Ľ–į 25 : –ď—Ä—É–Ņ–ł—Ä–į—ö–Ķ –Ĺ–į –Ī—Ä–ĺ—ė–Ĺ–ł –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł –≤–ĺ 5 –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł (–Ľ–Ķ–≤–ĺ) –ł –≤–ĺ 10 –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł (–ī–Ķ—Ā–Ĺ–ĺ) –ď—Ä–į—Ą–ł—á–ļ–ĺ –Ņ—Ä–Ķ—ā—Ā—ā–į–≤—É–≤–į—ö–Ķ –Ĺ–į –≥—Ä—É–Ņ–ł—Ä–į–Ĺ–ł—ā–Ķ –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł —Ā–ĺ —Ā–ĺ–ĺ–ī–≤–Ķ—ā–Ĺ–ł—ā–Ķ —Ä–Ķ–Ľ–į—ā–ł–≤–Ĺ–ł —Ö–ł—Ā—ā–ĺ–≥—Ä–į–ľ–ł –Ķ –ī–į–ī–Ķ–Ĺ–ł –≤–ĺ –°–Ľ–ł–ļ–į 22 –ł –°–Ľ–ł–ļ–į 23 . –ü–ĺ—Ā–Ķ–Ī–Ĺ–ĺ –Ĺ–Ķ –≥–ł –Ĺ–į–Ņ—Ä–į–≤–ł–≤–ľ–Ķ —Ä–Ķ–Ľ–į—ā–ł–≤–Ĺ–ł —á–Ķ—Ā—ā–ĺ—ā–Ĺ–ł —ā–į–Ī–Ķ–Ľ–ł –Ī–ł–ī–Ķ—ė—ú–ł —Ā–Ķ —Ä–į–Ī–ĺ—ā–ł –∑–į 100 –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł (–∑–Ĺ–į—á–ł —á–Ķ—Ā—ā–ĺ—ā–ł—ā–Ķ —Ā–Ķ –ł —Ā–į–ľ–ł ‚Äě—Ä–Ķ–Ľ–į—ā–ł–≤–Ĺ–ł‚Äú3).
–ě–ī —Ā—ā–į—ā–ł—Ā—ā–ł—á–Ĺ–į –≥–Ľ–Ķ–ī–Ĺ–į —ā–ĺ—á–ļ–į, –Ņ–ĺ–≤–Ķ—ú–Ķ –ł–Ĺ—Ą–ĺ—Ä–ľ–į—Ü–ł–ł —Ā–Ķ –ł–∑–≥—É–Ī–Ķ–Ĺ–ł –Ņ—Ä–ł –≥—Ä—É–Ņ–ł—Ä–į—ö–Ķ –Ĺ–į 5 –ĺ–ī —Ā–ĺ –≥—Ä—É–Ņ–ł—Ä–į—ö–Ķ –Ĺ–į 10 –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł. –ó–į–Ī–Ķ–Ľ–Ķ—ą–ļ–ł –≤–ĺ –ĺ–ī–Ĺ–ĺ—Ā –Ĺ–į –≥—Ä—É–Ņ—Ä–ł–į—ö–Ķ:
1 –í–ĺ –Ĺ–į–Ņ—Ä–Ķ–ī–Ĺ–į —Ā—ā–į—ā–ł—Ā—ā–ł–ļ–į[–ľ—Ä—ā–≤–į –≤—Ä—Ā–ļ–į] —ā–ł–Ņ–ĺ–≤–ł—ā–Ķ —Ā–ĺ –Ņ–ĺ–ī–Ķ–Ľ—É–≤–į–į—ā: –Ĺ–ĺ–ľ–ł–Ĺ–į–Ľ–Ĺ–ł, –ĺ—Ä–ī–ł–Ĺ–į–Ľ–Ĺ–ł, –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–Ĺ–ł –ł –ĺ–ī–Ĺ–ĺ—Ā–Ĺ–ł. –ú–Ķ—ď—É—ā–ĺ–į, —ā–į–ļ–≤–į –Ņ–ĺ–ī–Ķ–Ľ–Ī–į –Ĺ–Ķ –Ĺ–ł –Ņ–ĺ–ľ–į–≥–į –ľ–Ĺ–ĺ–≥—É –≤–ĺ –ĺ–Ņ–ł—Ā–Ĺ–į —Ā—ā–į—ā–ł—Ā—ā–ł–ļ–į. 2 –í–Ķ–Ľ–ł–ľ–Ķ ‚Äě–Ņ—Ä–ĺ–≥–Ľ–į—Ā–ł–ľ–Ķ‚Äú –Ī–ł–ī–Ķ—ė—ú–ł —Ā–Ķ–Ņ–į–ļ –∑–į–≤–ł—Ā–ł –ĺ–ī —Ā–ł—ā—É–į—ā—Ü–ł—ė–į—ā–į. –ü—Ä–ł –ĺ–≥—Ä–ĺ–ľ–Ķ–Ĺ –Ī—Ä–ĺ—ė –Ĺ–į –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł –ļ–į–ļ–ĺ –Ĺ–į –Ņ—Ä–ł–ľ–Ķ—Ä —Ä–Ķ–∑—É–Ľ—ā–į—ā–ł—ā–Ķ –ĺ–ī TOFEL –ł—Ā–Ņ–ł—ā –∑–į –Ņ–ĺ–∑–Ĺ–į–≤–į—ö–Ķ –Ĺ–į –į–Ĺ–≥–Ľ–ł—Ā–ļ–ł —ė–į–∑–ł–ļ –Ĺ–į –Ĺ–ł–≤–ĺ—ā–ĺ –Ĺ–į —Ā–≤–Ķ—ā–ĺ—ā, –ļ–į–ī–Ķ —ą—ā–ĺ —Ā–Ķ–Ņ–į–ļ —Ā–ł—ā–Ķ —Ä–Ķ–∑—É–Ľ–į—ā–ł —Ā–Ķ –ĺ–ī –Ī—Ä–ĺ–Ķ–≤–ł—ā–Ķ 1,2,...,100, –ł—Ā—ā–ł—ā–Ķ –ľ–ĺ–∂–į—ā –ī–į —Ā–Ķ —Ā–ľ–Ķ—ā–į–į—ā –∑–į –Ī—Ä–ĺ—ė–Ĺ–ł-–ļ–Ľ–į—Ā–ł. 3 –ě–≤–į –∑–Ĺ–į—á–ł –ī–Ķ–ļ–į –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł—ā–Ķ –Ī–ł —ā—Ä–Ķ–Ī–į–Ľ–ĺ –ī–į –Ī–ł–ī–į—ā —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł —Ä–Ķ–Ľ–į—ā–ł–≤–Ĺ–ĺ —É–Ĺ–ł—Ą–ĺ—Ä–ľ–Ĺ–ĺ (—Ä–į–≤–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ) –Ĺ–ł–∑ –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ĺ—ā [0,1]. –ú–Ķ—ď—É—ā–ĺ–į, —ā—É–ļ–į —Ā–Ķ —Ā–į–ľ–ĺ 100 –Ī—Ä–ĺ–Ķ–≤–ł —ā–į–ļ–į –ī–į –Ĺ–Ķ–ľ–į –ī–į –Ī–ł–ī–Ķ ‚Äě–ľ–Ĺ–ĺ–≥—É‚Äú —Ä–į–ľ–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ. –Ę—Ä–Ķ–Ī–į –ľ–Ĺ–ĺ–≥—É, –ľ–Ĺ–ĺ–≥—É, –ľ–Ĺ–ĺ–≥—É –Ņ–ĺ–ī–į—ā–ĺ—Ü–ł –∑–į —Ä–į–ľ–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ. (–°–ĺ–ĺ–ī–≤–Ķ—ā–Ĺ–į—ā–į –ļ–ĺ–ľ–į–Ĺ–ī–į –≤–ĺ –ēxcel –Ķ Rand().)
–õ–ł—ā–Ķ—Ä–į—ā—É—Ä–į–Ē—Ä—É–≥–ł —Ä–Ķ—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–ł |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia