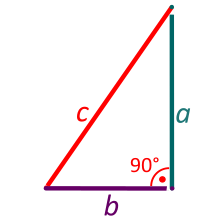
Правоаголен триаголник

Правоаголен триаголник
Правоаголен триаголник има прав агол
Рабови и темиња	3
Плоштина	½·a·b
Обем	a+b+c
Својства	прав агол испакнат

${\displaystyle a^{2}+b^{2}=c^{2}}$

Во долунаведените формули точката означува множење, т.е. ½ · b · h = ½ × b × h

Периметарот е збир на должините на трите страни

${\displaystyle L=a+b+c}$

Плоштина е:

• Плоштина на триаголник е една половина од основата помножена со висината, а бидејќи страната а е висината на основата b кај правоаголен триаголник имаме:

${\displaystyle P={\tfrac {1}{2}}\cdot a\cdot b}$.

Пример: Нека е даден правоаголен триаголник со катета a=5 cm и хипотенуза c=13 cm. Според Питагоровата теорема

${\displaystyle a^{2}+b^{2}=c^{2}\Rightarrow (5cm)^{2}+b^{2}=(13cm)^{2}\Rightarrow 25cm^{2}+b^{2}=169cm^{2}}$

${\displaystyle b^{2}=169cm^{2}-25cm^{2}\Rightarrow b^{2}=144cm^{2}\Rightarrow b={\sqrt {144cm^{2}}}\Rightarrow b=12cm}$

Пример: Нека е даден триаголник со катети а = b = 10mm. Според Питагоровата теорема

${\displaystyle a^{2}+b^{2}=c^{2}\Rightarrow (10mm)^{2}+(10mm)^{2}=c^{2}\Rightarrow 100mm^{2}+100mm^{2}=c^{2}}$

${\displaystyle 200mm^{2}=c^{2}\Rightarrow c^{2}=200mm^{2}\Rightarrow c={\sqrt {200mm^{2}}}\Rightarrow c=10{\sqrt {2}}\approx 14,14mm}$

Тригонометријата е гранка на математиката во која се разгледуваат своjствата на слични правоаголни триаголници. Два триаголници се слични ако имаат два пара на еднакви внатрешни агли. Во тој случај, автоматски и третиот пар агли се еднакви бидејќи збирот на аглите во триаголник е 180°. Значи, два правоаголни триаголници се слични ако еден пар од останатите два (остри) агли се еднакви. Ако два триаголници се слични, тогаш односот на кој било пар на страни е ист - тоа е дефиницијата за сличност. Затоа тригонометриските функции кои ги опишуваат односите на различните комбинации на страните на триаголникот зависат само од еден агол.

• Како и секој триаголник, правоаголниот триаголник е тетивен многуаголник, т.е. има впишана кружница (види триаголник).

Поставка: Центарот на впишаната кружница е пресекот на симетралите на внатрешни агли, а полупречникот r на впишаната кружница на правоаголен триаголник е:

${\displaystyle r={\frac {2P}{L}}={\frac {2\cdot {\tfrac {1}{2}}ab}{a+b+c}}={\frac {ab}{a+b+c}}}$

Впишана кружница на правоаголен триаголник; центарот е во пресекот на аголните симетрали.	Опишана кружница како последица од Талесовата теорема.	Опишана кружница на правоаголен триаголник; центарот е во средината Mc на хипотенузата c.

Талесова теорема гласи: Секој периферен агол над пречникот на кружница е прав агол.

Поставка: (Последица од Талесова теорема) Средината, т.е. средната точка на хипотенузата c на правоаголен триаголник е центарот на својата опишана кружница, а полупречникот на кружницата е половината од хипотенузата c:

${\displaystyle R={\frac {c}{2}}}$

Забелешка: Опишана кружница зависи само од хипотенузата, т.е. секој правоаголен триаголник со истата хипотенуза ја има истата опишана кружница.

Тежиштето e заеднички пресек на тежишните линии.	Инверзната Талесова теорема: Ако должината на тежишната линија CMc e c/2 тогаш ΔABC e правоаголен триаголник.

Во геометријата, тежишна линија на триаголник е отсечка која поврзува теме со средната точка на спротивната страна. Друг термин за тежишна линија е медијана.

• Теорема: Нека CM_c е тежнишната линија до најдолгата страна c=AB на триаголникот ΔABC. Должината на CM_c е еднаква на ^c/₂ ако и само ако ΔABC е правоаголен триаголник.^[4] (Доколку триаголник нема најдолга страна, тој не е правоаголен.)

Доказ: Талесовата теорема („ако“) и инверзната Талесова теорема („само ако“).^[5]

• Триаголник
• Питагорова теорема, Косинусова теорема
• Рамностран триаголник, Рамнокрак триаголник
• Складност на триаголници, Сличност на триаголници
• Талесова теорема

• Стојановска, Л. (2010). „Правоаголен триаголник“. Архивирано од изворникот на 2013-12-17. Посетено на 1 декември 2013. интерактивен
• Milanoff (2012). „Питагорова тройка 345“ (бугарски). Посетено на 1 декември 2013.^{[мртва врска]} интерактивен</ref>
• „Right Angle“. Math Open Reference. 2009. Посетено на 1 декември 2013. интерактивен