–Р–≤—В–Њ–Ї–Њ—А—А–µ–ї—П—Ж–Є–Њ–љ–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П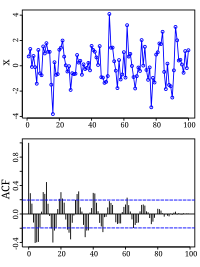 –Р–≤—В–Њ–Ї–Њ—А—А–µ–ї—П—Ж–Є–Њ–љ–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П (–Р–Ъ–§) вАФ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В—М –≤–Ј–∞–Є–Љ–Њ—Б–≤—П–Ј–Є –Љ–µ–ґ–і—Г —Д—Г–љ–Ї—Ж–Є–µ–є (—Б–Є–≥–љ–∞–ї–Њ–Љ) –Є –µ—С —Б–і–≤–Є–љ—Г—В–Њ–є –њ–Њ –∞—А–≥—Г–Љ–µ–љ—В—Г —Д—Г–љ–Ї—Ж–Є–Є –Ї–Њ–њ–Є–µ–є –Њ—В –≤–µ–ї–Є—З–Є–љ—Л —Б–і–≤–Є–≥–∞. –Ф–ї—П –і–µ—В–µ—А–Љ–Є–љ–Є—А–Њ–≤–∞–љ–љ—Л—Е —Б–Є–≥–љ–∞–ї–Њ–≤ –∞–≤—В–Њ–Ї–Њ—А—А–µ–ї—П—Ж–Є–Њ–љ–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П (–Р–Ъ–§) —Б–Є–≥–љ–∞–ї–∞ –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П –Є–љ—В–µ–≥—А–∞–ї–Њ–Љ: –Є –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В —Б–≤—П–Ј—М —Б–Є–≥–љ–∞–ї–∞ (—Д—Г–љ–Ї—Ж–Є–Є ) —Б –Ї–Њ–њ–Є–µ–є —Б–∞–Љ–Њ–≥–Њ —Б–µ–±—П, —Б–Љ–µ—Й—С–љ–љ–Њ–≥–Њ –љ–∞ –≤–µ–ї–Є—З–Є–љ—Г . –Ч–≤—С–Ј–і–Њ—З–Ї–∞ –Њ–Ј–љ–∞—З–∞–µ—В –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–Њ–µ —Б–Њ–њ—А—П–ґ–µ–љ–Є–µ. –Ф–ї—П —Б–ї—Г—З–∞–є–љ—Л—Е –њ—А–Њ—Ж–µ—Б—Б–Њ–≤ –Р–Ъ–§ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ –Є–Љ–µ–µ—В –≤–Є–і[1][2]:
–Ґ–∞–Ї–ґ–µ –≤ –ї–Є—В–µ—А–∞—В—Г—А–µ –Р–Ъ–§ —Б–ї—Г—З–∞–є–љ–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ –Њ–њ—А–µ–і–µ–ї—П—О—В –њ–Њ —Д–Њ—А–Љ—Г–ї–µ: –Т –љ–µ–Ї–Њ—В–Њ—А—Л—Е –Є—Б—В–Њ—З–љ–Є–Ї–∞—Е —Н—В—Г —Д—Г–љ–Ї—Ж–Є—О –љ–∞–Ј—Л–≤–∞—О—В –∞–≤—В–Њ–Ї–Њ–≤–∞—А–Є–∞—Ж–Є–Њ–љ–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–є[3]. –Х—Б–ї–Є –Є—Б—Е–Њ–і–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П —Б—В—А–Њ–≥–Њ –њ–µ—А–Є–Њ–і–Є—З–µ—Б–Ї–∞—П, —В–Њ –љ–∞ –≥—А–∞—Д–Є–Ї–µ –∞–≤—В–Њ–Ї–Њ—А—А–µ–ї—П—Ж–Є–Њ–љ–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є —В–Њ–ґ–µ –±—Г–і–µ—В —Б—В—А–Њ–≥–Њ –њ–µ—А–Є–Њ–і–Є—З–µ—Б–Ї–∞—П —Д—Г–љ–Ї—Ж–Є—П. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –Є–Ј —Н—В–Њ–≥–Њ –≥—А–∞—Д–Є–Ї–∞ –Љ–Њ–ґ–љ–Њ —Б—Г–і–Є—В—М –Њ –њ–µ—А–Є–Њ–і–Є—З–љ–Њ—Б—В–Є –Є—Б—Е–Њ–і–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є, –∞, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –Є –Њ –µ—С —З–∞—Б—В–Њ—В–љ—Л—Е —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–∞—Е. –Р–≤—В–Њ–Ї–Њ—А—А–µ–ї—П—Ж–Є–Њ–љ–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П –њ—А–Є–Љ–µ–љ—П–µ—В—Б—П –і–ї—П –∞–љ–∞–ї–Є–Ј–∞ —Б–ї–Њ–ґ–љ—Л—Е –Ї–Њ–ї–µ–±–∞–љ–Є–є, –љ–∞–њ—А–Є–Љ–µ—А, —Н–ї–µ–Ї—В—А–Њ—Н–љ—Ж–µ—Д–∞–ї–Њ–≥—А–∞–Љ–Љ—Л —З–µ–ї–Њ–≤–µ–Ї–∞. –Я—А–Є–Љ–µ–љ–µ–љ–Є–µ –≤ —В–µ—Е–љ–Є–Ї–µ–Ъ–Њ—А—А–µ–ї—П—Ж–Є–Њ–љ–љ—Л–µ —Б–≤–Њ–є—Б—В–≤–∞ –Ї–Њ–і–Њ–≤—Л—Е –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В–µ–є, –Є—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Л—Е –≤ —И–Є—А–Њ–Ї–Њ–њ–Њ–ї–Њ—Б–љ—Л—Е —Б–Є—Б—В–µ–Љ–∞—Е, –Ј–∞–≤–Є—Б—П—В –Њ—В —В–Є–њ–∞ –Ї–Њ–і–Њ–≤–Њ–є –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В–Є, –µ—С –і–ї–Є–љ—Л, —З–∞—Б—В–Њ—В—Л —Б–ї–µ–і–Њ–≤–∞–љ–Є—П –µ—С —Б–Є–Љ–≤–Њ–ї–Њ–≤ –Є –Њ—В –µ—С –њ–Њ—Б–Є–Љ–≤–Њ–ї—М–љ–Њ–є —Б—В—А—Г–Ї—В—Г—А—Л. –Ш–Ј—Г—З–µ–љ–Є–µ –∞–≤—В–Њ–Ї–Њ—А—А–µ–ї—П—Ж–Є–Њ–љ–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –Є–≥—А–∞–µ—В –≤–∞–ґ–љ—Г—О —А–Њ–ї—М –њ—А–Є –≤—Л–±–Њ—А–µ –Ї–Њ–і–Њ–≤—Л—Е –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В–µ–є —Б —В–Њ—З–Ї–Є –Ј—А–µ–љ–Є—П –љ–∞–Є–Љ–µ–љ—М—И–µ–є –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є —Г—Б—В–∞–љ–Њ–≤–ї–µ–љ–Є—П –ї–Њ–ґ–љ–Њ–є —Б–Є–љ—Е—А–Њ–љ–Є–Ј–∞—Ж–Є–Є. –Ф—А—Г–≥–Є–µ –њ—А–Є–Љ–µ–љ–µ–љ–Є—П–Р–≤—В–Њ–Ї–Њ—А—А–µ–ї—П—Ж–Є–Њ–љ–љ–∞—П —Д—Г–љ–Ї—Ж–Є—П –Є–≥—А–∞–µ—В –≤–∞–ґ–љ—Г—О —А–Њ–ї—М –≤ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–Љ –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є–Є –Є –∞–љ–∞–ї–Є–Ј–µ –≤—А–µ–Љ–µ–љ–љ—Л—Е —А—П–і–Њ–≤, –њ–Њ–Ї–∞–Ј—Л–≤–∞—П —Е–∞—А–∞–Ї—В–µ—А–љ—Л–µ –≤—А–µ–Љ–µ–љ–∞ –і–ї—П –Є—Б—Б–ї–µ–і—Г–µ–Љ—Л—Е –њ—А–Њ—Ж–µ—Б—Б–Њ–≤[4]. –Т —З–∞—Б—В–љ–Њ—Б—В–Є, —Ж–Є–Ї–ї–∞–Љ –≤ –њ–Њ–≤–µ–і–µ–љ–Є–Є –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Є—Е —Б–Є—Б—В–µ–Љ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—В –Љ–∞–Ї—Б–Є–Љ—Г–Љ—Л –∞–≤—В–Њ–Ї–Њ—А—А–µ–ї—П—Ж–Є–Њ–љ–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –љ–µ–Ї–Њ—В–Њ—А–Њ–≥–Њ —Е–∞—А–∞–Ї—В–µ—А–љ–Њ–≥–Њ –њ–∞—А–∞–Љ–µ—В—А–∞. –°–Љ. —В–∞–Ї–ґ–µ
–Я—А–Є–Љ–µ—З–∞–љ–Є—П
–°—Б—Л–ї–Ї–Є |
Portal di Ensiklopedia Dunia





![{\displaystyle B(t,t-\tau )=\mathbb {E} [X(t)X^{*}(t-\tau )]=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }x_{1}x_{2}^{*}f_{2}(x_{1},t;x_{2},t-\tau )dx_{1}dx_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/757570312ef664f0a4adda263d5a3a91883646d4)








![{\displaystyle {\begin{aligned}B(t,t-\tau )=\mathbb {E} [(X(t)-\mathbb {E} [X(t)])(X^{*}(t-\tau )-\mathbb {E} [X^{*}(t-\tau )])]=\\=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }(x_{1}-\mathbb {E} [X(t)])(x_{2}^{*}-\mathbb {E} [X^{*}(t-\tau )])f_{2}(x_{1},t;x_{2},t-\tau )dx_{1}dx_{2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee3ea1b73d6c0081e721a01eeb515ea094a37000)













