–ö–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ (—ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—Ź) –ö–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –≤ —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł–ł ‚ÄĒ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –Ĺ–į–Ī–ĺ—Ä–ĺ–≤ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ –∑–į–ī–į–Ĺ–Ĺ–ĺ–≥–ĺ —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į. –í—č–ī–Ķ–Ľ—Ź—é—ā –ī–≤–į —ā–ł–Ņ–į –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ—č—Ö –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤: –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ —É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ—č—Ö –Ĺ–į–Ī–ĺ—Ä–ĺ–≤ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ –ī–į–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –ł –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –Ĺ–Ķ—É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ—č—Ö –Ĺ–į–Ī–ĺ—Ä–ĺ–≤ –Ķ–≥–ĺ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ, –≥–ī–Ķ . –í–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ–ü–ĺ–Ĺ—Ź—ā–ł–Ķ –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –Ķ—Ā—ā–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –≤–ĺ–∑–Ĺ–ł–ļ–į–Ķ—ā –≤–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–Ķ –ĺ–Ī–Ľ–į—Ā—ā–Ķ–Ļ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–ł –ł –Ķ—Ď –Ņ—Ä–ł–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ļ. –ö–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ—č–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–Ķ–Ļ, —ā–į–ļ–ł—Ö –ļ–į–ļ –Ķ–≤–ļ–Ľ–ł–ī–ĺ–≤–į –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā—Ć –ł —Ā—Ą–Ķ—Ä–į , —ā–Ķ—Ā–Ĺ–ĺ —Ā–≤—Ź–∑–į–Ĺ—č —Ā —ā–Ķ–ĺ—Ä–ł–Ķ–Ļ –ļ–ĺ—Ā –ł –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į–ľ–ł –ľ–ĺ–ī—É–Ľ–Ķ–Ļ. –ö—Ä–ĺ–ľ–Ķ —ā–ĺ–≥–ĺ, –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ—č–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –ľ–Ĺ–ĺ–≥–ĺ–ĺ–Ī—Ä–į–∑–ł–Ļ –≤–ĺ–∑–Ĺ–ł–ļ–į—é—ā –≤ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö –∑–į–ī–į—á–į—Ö –į–Ľ–≥–Ķ–Ī—Ä–į–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł–ł –ł –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ—č –ī–Ľ—Ź –≥–ĺ–ľ–ĺ—ā–ĺ–Ņ–ł—á–Ķ—Ā–ļ–ĺ–Ļ –į–Ņ–Ņ—Ä–ĺ–ļ—Ā–ł–ľ–į—Ü–ł–ł –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤ –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ—č—Ö –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ļ. –®–ł—Ä–ĺ–ļ–ł–Ķ –Ņ—Ä–ł–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –ī–ĺ–Ņ—É—Ā–ļ–į–Ķ—ā –∑–į–ī–į—á–į –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź –≥–ĺ–ľ–ĺ—ā–ĺ–Ņ–ł—á–Ķ—Ā–ļ–ł—Ö —ā–ł–Ņ–ĺ–≤ –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ—č—Ö –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –Ĺ–į–Ī–ĺ—Ä–ĺ–≤ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ –Ķ–≤–ļ–Ľ–ł–ī–ĺ–≤–į –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ķ—Ā—ā–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–ľ –ļ–ĺ–Ĺ—ā–Ķ–ļ—Ā—ā–ĺ–ľ –≥—Ä–į–≤–ł—ā–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–Ļ –∑–į–ī–į—á–ł —ā–Ķ–Ľ. –Ę–į–ļ, —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł–Ķ –Ņ–Ķ—Ä–ł–ĺ–ī–ł—á–Ķ—Ā–ļ–ł—Ö —Ä–Ķ—ą–Ķ–Ĺ–ł–Ļ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–Ķ–Ļ –≥–į–ľ–ł–Ľ—Ć—ā–ĺ–Ĺ–ĺ–≤–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ—č –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–ĺ –Ņ—É—ā—Ď–ľ –ł–∑—É—á–Ķ–Ĺ–ł—Ź –ļ–į—ā–Ķ–≥–ĺ—Ä–ł–ł –õ—é—Ā—ā–Ķ—Ä–Ĺ–ł–ļ–į ‚ÄĒ –®–Ĺ–ł—Ä–Ķ–Ľ—Ć–ľ–į–Ĺ–į –ł —Ä—Ź–ī–į –ü—É–į–Ĺ–ļ–į—Ä–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –Ņ–Ķ—ā–Ķ–Ľ—Ć [1]. –ö–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ—č–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –≤–ĺ–∑–Ĺ–ł–ļ–į—é—ā –≤ –∑–į–ī–į—á–į—Ö, –ł–∑–≤–Ķ—Ā—ā–Ĺ—č—Ö –Ņ–ĺ–ī –ĺ–Ī—Č–ł–ľ –ł–ľ–Ķ–Ĺ–Ķ–ľ ¬ę–Ę—Ä–ł–Ĺ–į–ī—Ü–į—ā–į—Ź –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–į –ď–ł–Ľ—Ć–Ī–Ķ—Ä—ā–į¬Ľ, –į –ł–ľ–Ķ–Ĺ–Ĺ–ĺ, –≤ –∑–į–ī–į—á–Ķ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł—Ź (–ľ–Ĺ–ĺ–≥–ĺ–∑–Ĺ–į—á–Ĺ—č—Ö) –į–Ľ–≥–Ķ–Ī—Ä–į–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ –ĺ—ā –Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ł—Ö –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č—Ö –≤ –≤–ł–ī–Ķ –ļ–ĺ–ľ–Ņ–ĺ–∑–ł—Ü–ł–ł —Ą—É–Ĺ–ļ—Ü–ł–Ļ –ľ–Ķ–Ĺ—Ć—ą–Ķ–≥–ĺ —á–ł—Ā–Ľ–į –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č—Ö[2]. –ö–Ľ–į—Ā—Ā–ł—á–Ķ—Ā–ļ–ł–ľ –Ņ—Ä–ł–ľ–Ķ—Ä–ĺ–ľ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į –≤ –ī–į–Ĺ–Ĺ–ĺ–ľ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–ł —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ –ĺ —ā–ĺ–ľ, —á—ā–ĺ –Ņ—Ä–ł —Ą—É–Ĺ–ļ—Ü–ł—Ź, —Ā–ĺ–Ņ–ĺ—Ā—ā–į–≤–Ľ—Ź—é—Č–į—Ź –Ĺ–į–Ī–ĺ—Ä—É –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ—č—Ö —á–ł—Ā–Ķ–Ľ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –ł–∑ –ļ–ĺ—Ä–Ĺ–Ķ–Ļ –ľ–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ–į
–Ĺ–Ķ –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–į –≤ –≤–ł–ī–Ķ –ļ–ĺ–ľ–Ņ–ĺ–∑–ł—Ü–ł–ł —Ą—É–Ĺ–ļ—Ü–ł–Ļ –ľ–Ķ–Ĺ—Ć—ą–Ķ–≥–ĺ —á–Ķ–ľ —á–ł—Ā–Ľ–į –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č—Ö[3]. –í 1970 –≥–ĺ–ī—É –í–Ľ–į–ī–ł–ľ–ł—Ä –ė–≥–ĺ—Ä–Ķ–≤–ł—á –ź—Ä–Ĺ–ĺ–Ľ—Ć–ī –Ņ—Ä–Ķ–ī–Ľ–ĺ–∂–ł–Ľ –Ņ–ĺ–ī—Ö–ĺ–ī –ļ —ć—ā–ĺ–Ļ –∑–į–ī–į—á–Ķ, –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–Ĺ—č–Ļ –Ĺ–į –Ņ–ĺ–ī—Ā—á—Ď—ā–Ķ –≥—Ä—É–Ņ–Ņ –ļ–ĺ–≥–ĺ–ľ–ĺ–Ľ–ĺ–≥–ł–Ļ[–į–Ĺ–≥–Ľ.] –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł , –ł –ī–ĺ–ļ–į–∑–į–Ľ –ī–į–Ĺ–Ĺ–ĺ–Ķ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ –≤ —Ā–Ľ—É—á–į–Ķ, –Ķ—Ā–Ľ–ł —á–ł—Ā–Ľ–ĺ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ā—ā–Ķ–Ņ–Ķ–Ĺ—Ć—é –ī–≤–ĺ–Ļ–ļ–ł[4]. –†–ĺ–ī—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–ľ –ļ –ī–į–Ĺ–Ĺ–ĺ–ľ—É —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ķ—Ā—ā–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–Ķ –≤–ĺ–∑–Ĺ–ł–ļ–Ĺ–ĺ–≤–Ķ–Ĺ–ł–Ķ –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ—č—Ö –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤ –≤ —ā–Ķ–ĺ—Ä–ł–ł –Ĺ–į–ļ—Ä—č—ā–ł–Ļ. –Ę–į–ļ, –ļ–į–∂–ī–ĺ–Ķ -–Ľ–ł—Ā—ā–Ĺ–ĺ–Ķ –Ĺ–į–ļ—Ä—č—ā–ł–Ķ –∑–į–ī–į—Ď—ā –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ–ĺ–Ķ –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ , —Ā–ĺ–Ņ–ĺ—Ā—ā–į–≤–Ľ—Ź—é—Č–Ķ–Ķ —ā–ĺ—á–ļ–Ķ –Ķ—Ď –Ņ–ĺ–Ľ–Ĺ—č–Ļ –Ņ—Ä–ĺ–ĺ–Ī—Ä–į–∑ . –Ē–į–Ĺ–Ĺ–ĺ–Ķ –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –ł–Ĺ–ī—É—Ü–ł—Ä—É–Ķ—ā –≥–ĺ–ľ–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ —Ą—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ—Ć–Ĺ—č—Ö –≥—Ä—É–Ņ–Ņ
–≥–ī–Ķ ‚ÄĒ —ā–į–ļ –Ĺ–į–∑—č–≤–į–Ķ–ľ–į—Ź –≥—Ä—É–Ņ–Ņ–į –ļ–ĺ—Ā —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į . –≠—ā–ĺ—ā –≥–ĺ–ľ–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≤–į–∂–Ĺ—č–ľ –ł–Ĺ–≤–į—Ä–ł–į–Ĺ—ā–ĺ–ľ –Ĺ–į–ļ—Ä—č—ā–ł—Ź [5]. –ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ–ö–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ —É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ—č—Ö –Ĺ–į–Ī–ĺ—Ä–ĺ–≤ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į ‚ÄĒ —ć—ā–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ -–ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā–Ĺ—č—Ö –ļ–ĺ—Ä—ā–Ķ–∂–Ķ–Ļ –Ņ–ĺ–Ņ–į—Ä–Ĺ–ĺ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ĺ–≤ –ł–∑ , —ā–ĺ –Ķ—Ā—ā—Ć –Ņ–ĺ–ī–ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ[6]
–ī–Ķ–ļ–į—Ä—ā–ĺ–≤–ĺ–Ļ —Ā—ā–Ķ–Ņ–Ķ–Ĺ–ł , —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į–Ķ–ľ–ĺ–Ķ —Ā —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł–Ķ–Ļ, –ł–Ĺ–ī—É—Ü–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ļ —Ā —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł–ł –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—Ź –Ĺ–į . –Ę–į–ļ–∂–Ķ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—é—ā—Ā—Ź –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź [7], [8] –ł [1]. –ö–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –Ĺ–Ķ—É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ—č—Ö –Ĺ–į–Ī–ĺ—Ä–ĺ–≤ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į ‚ÄĒ —ć—ā–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –Ķ–≥–ĺ -—ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–Ĺ—č—Ö –Ņ–ĺ–ī–ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤[9]. –ė–Ĺ—č–ľ–ł —Ā–Ľ–ĺ–≤–į–ľ–ł, —ć—ā–ĺ —Ą–į–ļ—ā–ĺ—Ä–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –Ņ–ĺ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—é, –Ņ—Ä–ł –ļ–ĺ—ā–ĺ—Ä–ĺ–ľ –ī–≤–į –ļ–ĺ—Ä—ā–Ķ–∂–į —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ—č, –Ķ—Ā–Ľ–ł –ĺ–ī–ł–Ĺ –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ –ł–∑ –ī—Ä—É–≥–ĺ–≥–ĺ –Ņ–Ķ—Ä–Ķ—Ā—ā–į–Ĺ–ĺ–≤–ļ–ĺ–Ļ –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā. –Ę–į–ļ–∂–Ķ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—é—ā—Ā—Ź –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź [7], [10] –ł [11]. –í –≤—č—Ä–ĺ–∂–ī–Ķ–Ĺ–Ĺ–ĺ–ľ —Ā–Ľ—É—á–į–Ķ –ł–ľ–Ķ—é—ā—Ā—Ź —Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–į . –í –Ľ–ł—ā–Ķ—Ä–į—ā—É—Ä–Ķ —ā–į–ļ–∂–Ķ –≤—Ā—ā—Ä–Ķ—á–į—é—ā—Ā—Ź —Ā–Ľ–Ķ–ī—É—é—Č–ł–Ķ –ľ–ĺ–ī–ł—Ą–ł–ļ–į—Ü–ł–ł –Ņ—Ä–Ķ–ī—č–ī—É—Č–ł—Ö –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—Ü–ł–Ļ. –ü—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –ļ–ĺ–Ĺ–Ķ—á–Ĺ—č—Ö —É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ—č—Ö –Ĺ–į–Ī–ĺ—Ä–ĺ–≤ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į ‚ÄĒ —ć—ā–ĺ –ī–ł–∑—ä—é–Ĺ–ļ—ā–Ĺ–ĺ–Ķ –ĺ–Ī—ä–Ķ–ī–ł–Ĺ–Ķ–Ĺ–ł–Ķ
–ü—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –ļ–ĺ–Ĺ–Ķ—á–Ĺ—č—Ö –Ņ–ĺ–ī–ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤ —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į ‚ÄĒ —ć—ā–ĺ –ī–ł–∑—ä—é–Ĺ–ļ—ā–Ĺ–ĺ–Ķ –ĺ–Ī—ä–Ķ–ī–ł–Ĺ–Ķ–Ĺ–ł–Ķ
–°–≤–ĺ–Ļ—Ā—ā–≤–į–ö–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ—č–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ—č—Ö —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ł—Ö –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤ –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ—č. –í —Ā–Ľ—É—á–į–Ķ, –Ķ—Ā–Ľ–ł —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ł–ľ –ľ–Ĺ–ĺ–≥–ĺ–ĺ–Ī—Ä–į–∑–ł–Ķ–ľ (–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ, —Ā –Ĺ–Ķ–Ņ—É—Ā—ā—č–ľ –ļ—Ä–į–Ķ–ľ) —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł , –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –ł —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –ľ–Ĺ–ĺ–≥–ĺ–ĺ–Ī—Ä–į–∑–ł—Ź–ľ–ł —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł . –ö—Ä–ĺ–ľ–Ķ —ā–ĺ–≥–ĺ, –Ķ—Ā–Ľ–ł —Ā–≤—Ź–∑–Ĺ–ĺ –ł , —ā–ĺ –ĺ–Ī–į –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –ł —Ā–≤—Ź–∑–Ĺ—č[6]. –ö–į–Ĺ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–į—Ź –Ņ—Ä–ĺ–Ķ–ļ—Ü–ł—Ź —Ā–ĺ–≤–Ņ–į–ī–į–Ķ—ā —Ā –ļ–į–Ĺ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–ĺ–Ļ –Ņ—Ä–ĺ–Ķ–ļ—Ü–ł–Ķ–Ļ –Ĺ–į —Ą–į–ļ—ā–ĺ—Ä–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –Ņ–ĺ —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–ľ—É –ī–Ķ–Ļ—Ā—ā–≤–ł—é —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ—č:
–ü–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É –ī–į–Ĺ–Ĺ–ĺ–Ķ –ī–Ķ–Ļ—Ā—ā–≤–ł–Ķ –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ–ĺ –ł –≤–Ņ–ĺ–Ľ–Ĺ–Ķ —Ä–į–∑—Ä—č–≤–Ĺ–ĺ, –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ĺ–į–ļ—Ä—č—ā–ł–Ķ–ľ, –Ņ—Ä–ł—á–Ķ–ľ —Ä–Ķ–≥—É–Ľ—Ź—Ä–Ĺ—č–ľ. –ß–ł—Ā–Ľ–ĺ –Ķ–≥–ĺ –Ľ–ł—Ā—ā–ĺ–≤ —Ä–į–≤–Ĺ–ĺ –Ņ–ĺ—Ä—Ź–ī–ļ—É –≥—Ä—É–Ņ–Ņ—č , —ā–ĺ –Ķ—Ā—ā—Ć . –ē–≤–ļ–Ľ–ł–ī–ĺ–≤—č –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į–ö–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ—č–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—č—Ö –Ķ–≤–ļ–Ľ–ł–ī–ĺ–≤—č—Ö –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤ –ľ–ĺ–∂–Ĺ–ĺ –ĺ–Ņ–ł—Ā–į—ā—Ć –≤ —Ā–Ľ–Ķ–ī—É—é—Č–ł—Ö —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ—č—Ö —ā–Ķ—Ä–ľ–ł–Ĺ–į—Ö. –ü—Ä—Ź–ľ–į—Ź–í–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–į—Ź –Ņ—Ä—Ź–ľ–į—Ź –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ–į –Ķ–ī–ł–Ĺ–ł—á–Ĺ–ĺ–ľ—É –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ—É , –Ņ–ĺ—ć—ā–ĺ–ľ—É –ī–Ľ—Ź –ł–∑—É—á–Ķ–Ĺ–ł—Ź —Ā—ā—Ä—É–ļ—ā—É—Ä—č –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ—č—Ö –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤ –Ņ—Ä—Ź–ľ–ĺ–Ļ –ī–ĺ—Ā—ā–į—ā–ĺ—á–Ĺ–ĺ —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—ā—Ć –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ—č–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į —ā–į–ļ–ĺ–≥–ĺ –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–į. –ě–Ĺ–ł, –≤ —Ā–≤–ĺ—é –ĺ—á–Ķ—Ä–Ķ–ī—Ć, –ī–ĺ–Ņ—É—Ā–ļ–į—é—ā —Ā–Ľ–Ķ–ī—É—é—Č–ł–Ķ –ĺ–Ņ–ł—Ā–į–Ĺ–ł—Ź.  –ö–į–∂–ī—č–Ļ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –Ĺ–Ķ—É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ—č—Ö –Ĺ–į–Ī–ĺ—Ä–ĺ–≤ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–į –∑–į–ī–į—Ď—ā—Ā—Ź —ā–į–ļ–ĺ–Ļ –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā—Ć—é –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č—Ö —á–ł—Ā–Ķ–Ľ, —á—ā–ĺ
–Ě–Ķ–Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –ł–∑ –Ķ–≥–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź —Ā–Ľ–Ķ–ī—É–Ķ—ā, —á—ā–ĺ —ā–į–ļ–į—Ź –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā—Ć —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É–Ķ—ā –≤–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ–Ķ–Ļ —ā–ĺ—á–ļ–Ķ —Ā–ł–ľ–Ņ–Ľ–Ķ–ļ—Ā–į —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł , –Ņ—Ä–ł—á–Ķ–ľ –ī–į–Ĺ–Ĺ–į—Ź –ļ–ĺ–ī–ł—Ä–ĺ–≤–ļ–į –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ–ĺ –∑–į–≤–ł—Ā–ł—ā –ĺ—ā –ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–Ļ –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł. –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ–ĺ –≤–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ–ĺ—Ā—ā–ł -–ľ–Ķ—Ä–Ĺ–ĺ–≥–ĺ —Ā–ł–ľ–Ņ–Ľ–Ķ–ļ—Ā–į[12]. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ–ĺ –≤–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ–ĺ—Ā—ā–ł —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į, –į –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ ‚ÄĒ –≤–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ–ĺ—Ā—ā–ł —ā–Ķ—ā—Ä–į—ć–ī—Ä–į. –ö–į–∂–ī—č–Ļ –Ĺ–Ķ—É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ—č–Ļ –Ĺ–į–Ī–ĺ—Ä —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ –Ķ–ī–ł–Ĺ–ł—á–Ĺ–ĺ–≥–ĺ –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–į –ľ–ĺ–∂–Ĺ–ĺ —É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–ł—ā—Ć —Ä–ĺ–≤–Ĺ–ĺ —Ā–Ņ–ĺ—Ā–ĺ–Ī–į–ľ–ł. –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ–ĺ –ī–ł–∑—ä—é–Ĺ–ļ—ā–Ĺ–ĺ–ľ—É –ĺ–Ī—ä–Ķ–ī–ł–Ĺ–Ķ–Ĺ–ł—é –ļ–ĺ–Ņ–ł–Ļ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į . –í —á–į—Ā—ā–Ĺ–ĺ—Ā—ā–ł, –ļ–į–∂–ī–į—Ź –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā–į —Ā–≤—Ź–∑–Ĺ–ĺ—Ā—ā–ł –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤ –ł —Ā—ā—Ź–≥–ł–≤–į–Ķ–ľ–į. –Ď–ĺ–Ľ–Ķ–Ķ —ā–ĺ–≥–ĺ, –≤ –ĺ–Ī–ĺ–ł—Ö —Ā–Ľ—É—á–į—Ź—Ö –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–Ļ, –≤ –ļ–ĺ—ā–ĺ—Ä—č—Ö —Ā–ĺ—Ā–Ķ–ī–Ĺ–ł–Ķ —ā–ĺ—á–ļ–ł (–≤–ľ–Ķ—Ā—ā–Ķ —Ā —ā–ĺ—á–ļ–į–ľ–ł –ł ) —Ä–į–≤–Ĺ–ĺ—É–ī–į–Ľ–Ķ–Ĺ—č –ī—Ä—É–≥ –ĺ—ā –ī—Ä—É–≥–į, —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ī–Ķ—Ą–ĺ—Ä–ľ–į—Ü–ł–ĺ–Ĺ–Ĺ—č–ľ —Ä–Ķ—ā—Ä–į–ļ—ā–ĺ–ľ –ĺ–Ī—ä–Ķ–ľ–Ľ—é—Č–Ķ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į: –ļ–į–∂–ī—č–Ļ ¬ę–Ĺ–Ķ—Ä–ĺ–≤–Ĺ—č–Ļ¬Ľ –Ĺ–į–Ī–ĺ—Ä –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –ī–Ķ—Ą–ĺ—Ä–ľ–ł—Ä–ĺ–≤–į–Ĺ –≤ ¬ę—Ä–ĺ–≤–Ĺ—č–Ļ¬Ľ –Ņ—É—ā—Ď–ľ —Ä–į–≤–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ–≥–ĺ —Ä–į—Ā—ā–į–Ľ–ļ–ł–≤–į–Ĺ–ł—Ź –ł–Ľ–ł —Ā–Ī–Ľ–ł–∂–Ķ–Ĺ–ł—Ź –Ķ–≥–ĺ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ĺ–≤. –ü–į—Ä—č —ā–ĺ—á–Ķ–ļ –≤ –Ķ–≤–ļ–Ľ–ł–ī–ĺ–≤—č—Ö –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į—Ö–ü–į—Ä–į —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ –Ĺ–į –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł –ĺ–ī–Ĺ–ĺ–∑–Ĺ–į—á–Ĺ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–Ķ—Ä–≤–ĺ–Ļ —ā–ĺ—á–ļ–ĺ–Ļ –ł –≤–Ķ–ļ—ā–ĺ—Ä–ĺ–ľ , –ĺ—ā–≤–Ķ—á–į—é—Č–Ķ–ľ –∑–į —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ –≤—ā–ĺ—Ä–ĺ–Ļ —ā–ĺ—á–ļ–ł –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ņ–Ķ—Ä–≤–ĺ–Ļ. –Ē–į–Ĺ–Ĺ–į—Ź –ļ–ĺ–ī–ł—Ä–ĺ–≤–ļ–į –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ–ĺ –∑–į–≤–ł—Ā–ł—ā –ĺ—ā –ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–Ļ –Ņ–į—Ä—č —ā–ĺ—á–Ķ–ļ. –°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ —ā–į–ļ–ł—Ö —ā–ĺ—á–Ķ–ļ –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ–ĺ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—é –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł –ł –Ņ—Ä–ĺ–ļ–ĺ–Ľ–ĺ—ā–ĺ–Ļ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł:
–Ē–į–Ĺ–Ĺ—č–Ļ –Ņ–ĺ–ī—Ö–ĺ–ī –ĺ–Ī–ĺ–Ī—Č–į–Ķ—ā—Ā—Ź –Ĺ–į –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ–ĺ–Ķ –Ķ–≤–ļ–Ľ–ł–ī–ĺ–≤–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ . –ź –ł–ľ–Ķ–Ĺ–Ĺ–ĺ, –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ —É—Ā—ā–į–Ĺ–į–≤–Ľ–ł–≤–į–Ķ—ā –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ
–í –ĺ–Ī—Č–Ķ–ľ —Ā–Ľ—É—á–į–Ķ –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ —É—Ā—ā–į–Ĺ–į–≤–Ľ–ł–≤–į–Ķ—ā –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ[13]
 –ü–ĺ—Ö–ĺ–∂—É—é –ļ–ĺ–ī–ł—Ä–ĺ–≤–ļ—É –ī–ĺ–Ņ—É—Ā–ļ–į–Ķ—ā –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –ī–≤—É—Ö—ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–Ĺ—č—Ö –Ņ–ĺ–ī–ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤ –Ķ–≤–ļ–Ľ–ł–ī–ĺ–≤–į –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į . –Ę–į–ļ, –Ņ–ĺ–ī–ĺ–Ī–Ĺ—č–Ķ –Ņ–ĺ–ī–ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–į –ĺ–ī–Ĺ–ĺ–∑–Ĺ–į—á–Ĺ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—é—ā—Ā—Ź —Ā–≤–ĺ–ł–ľ —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –ľ–į—Ā—Ā , —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ–ľ –ł –Ņ—Ä—Ź–ľ–ĺ–Ļ, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–Ķ–Ļ —á–Ķ—Ä–Ķ–∑ —ć—ā–ł —ā–ĺ—á–ļ–ł, –ļ–ĺ—ā–ĺ—Ä–į—Ź –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ–Ķ–ļ—ā–ł–≤–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į[–į–Ĺ–≥–Ľ.] —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł . –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ,
–í —á–į—Ā—ā–Ĺ–ĺ—Ā—ā–ł, –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –ł –≥–ĺ–ľ–ĺ—ā–ĺ–Ņ–ł—á–Ķ—Ā–ļ–ł —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ—č, —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ, –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į–ľ –ł . –ü–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā—Ć–ö–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –Ĺ–Ķ—É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ—č—Ö –Ĺ–į–Ī–ĺ—Ä–ĺ–≤ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł –ī–ĺ–Ņ—É—Ā–ļ–į–Ķ—ā —Ā–Ľ–Ķ–ī—É—é—Č—É—é[14] –ł–Ĺ—ā–Ķ—Ä–Ņ—Ä–Ķ—ā–į—Ü–ł—é –≤ —ā–Ķ—Ä–ľ–ł–Ĺ–į—Ö –ľ–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ–ĺ–≤ –Ī–Ķ–∑ –ļ—Ä–į—ā–Ĺ—č—Ö –ļ–ĺ—Ä–Ĺ–Ķ–Ļ, –Ņ—Ä–Ķ–ī–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ—É—é –í–Ľ–į–ī–ł–ľ–ł—Ä–ĺ–ľ –ė–≥–ĺ—Ä–Ķ–≤–ł—á–Ķ–ľ –ź—Ä–Ĺ–ĺ–Ľ—Ć–ī–ĺ–ľ –≤ –Ķ–≥–ĺ —Ä–į–Ī–ĺ—ā–Ķ 1970 –≥–ĺ–ī–į[15]. –ě—ā–ĺ–∂–ī–Ķ—Ā—ā–≤–ł–ľ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā—Ć —Ā –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ–Ļ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā—Ć—é . –ú–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –≤—Ā–Ķ—Ö –Ņ—Ä–ł–≤–Ķ–ī—Ď–Ĺ–Ĺ—č—Ö –ľ–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ–ĺ–≤ —Ā—ā–Ķ–Ņ–Ķ–Ĺ–ł –ĺ–ī–Ĺ–ĺ–Ļ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ–Ļ –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ, —ā–ĺ –Ķ—Ā—ā—Ć –ľ–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ–ĺ–≤ –≤–ł–ī–į
–≥–ī–Ķ , –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –ĺ—ā–ĺ–∂–ī–Ķ—Ā—ā–≤–Ľ–Ķ–Ĺ–ĺ —Ā –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ–ľ . –°–ĺ–≥–Ľ–į—Ā–Ĺ–ĺ –ĺ—Ā–Ĺ–ĺ–≤–Ĺ–ĺ–Ļ —ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ –į–Ľ–≥–Ķ–Ī—Ä—č, —Ā–ĺ–Ņ–ĺ—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł–Ķ –Ĺ–į–Ī–ĺ—Ä—É –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ—č—Ö —á–ł—Ā–Ķ–Ľ –ľ–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ–į –∑–į–ī–į—Ď—ā —Ā—é—Ä—ä–Ķ–ļ—ā–ł–≤–Ĺ–ĺ–Ķ –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—Ź –≤ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ —ā–į–ļ–ł—Ö –ľ–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ–ĺ–≤. –í —ā–Ķ—Ä–ľ–ł–Ĺ–į—Ö –Ņ—Ä–Ķ–ī—č–ī—É—Č–Ķ–≥–ĺ –ĺ—ā–ĺ–∂–ī–Ķ—Ā—ā–≤–Ľ–Ķ–Ĺ–ł—Ź –ĺ–Ĺ–ĺ –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –∑–į–ī–į–Ĺ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–ĺ–Ļ
–≥–ī–Ķ ‚ÄĒ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ–ĺ–≥–ĺ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –ľ–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ–į —Ā—ā–Ķ–Ņ–Ķ–Ĺ–ł –ĺ—ā –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č—Ö –Ĺ–į –ļ–ĺ—Ä—ā–Ķ–∂–Ķ . –ě–Ī—Ä–į–∑–ĺ–ľ —Ā—É–∂–Ķ–Ĺ–ł—Ź —ć—ā–ĺ–≥–ĺ –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł—Ź –Ĺ–į –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –ľ–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ–ĺ–≤ –Ī–Ķ–∑ –ļ—Ä–į—ā–Ĺ—č—Ö –ļ–ĺ—Ä–Ĺ–Ķ–Ļ. –Ē–į–Ĺ–Ĺ–ĺ–Ķ —Ā—É–∂–Ķ–Ĺ–ł–Ķ –ł–Ĺ–ī—É—Ü–ł—Ä—É–Ķ—ā –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ –ľ–Ķ–∂–ī—É –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ—č–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ–ľ –ł –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ–ľ –Ņ—Ä–ł–≤–Ķ–ī—Ď–Ĺ–Ĺ—č—Ö –ľ–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ–ĺ–≤ —Ā—ā–Ķ–Ņ–Ķ–Ĺ–ł –Ī–Ķ–∑ –ļ—Ä–į—ā–Ĺ—č—Ö –ļ–ĺ—Ä–Ĺ–Ķ–Ļ –ĺ–ī–Ĺ–ĺ–Ļ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ–Ļ –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ. –ė–∑—É—á–Ķ–Ĺ–ł–Ķ —Ā–≤–ĺ–Ļ—Ā—ā–≤ –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ–į, –ĺ–Ī—Ä–į—ā–Ĺ–ĺ–≥–ĺ –ļ —É–ļ–į–∑–į–Ĺ–Ĺ–ĺ–ľ—É –≤—č—ą–Ķ, —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ĺ–ī–Ĺ–ĺ–Ļ –ł–∑ –ĺ—Ā–Ĺ–ĺ–≤–Ĺ—č—Ö —ā–Ķ–ľ –≤ –ļ–Ľ–į—Ā—Ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ā–Ķ–ĺ—Ä–ł–ł –ď–į–Ľ—É–į[13]. –Ę—Ä–ĺ–Ļ–ļ–ł —ā–ĺ—á–Ķ–ļ –Ĺ–į –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł –ö–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ —ā—Ä—Ď—Ö—ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–Ĺ—č—Ö –Ņ–ĺ–ī–ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ–Ļ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł –ł –≤–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ–ĺ—Ā—ā—Ć –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł—Ź —É–∑–Ľ–į —ā—Ä–ł–Ľ–ł—Ā—ā–Ĺ–ł–ļ–į –≥–ĺ–ľ–ĺ—ā–ĺ–Ņ–ł—á–Ķ—Ā–ļ–ł —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ—č. –Ē–į–Ĺ–Ĺ–į—Ź –≥–ĺ–ľ–ĺ—ā–ĺ–Ņ–ł—á–Ķ—Ā–ļ–į—Ź —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ–ĺ—Ā—ā—Ć –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć —É—Ā—ā–į–Ĺ–ĺ–≤–Ľ–Ķ–Ĺ–į —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ[16]. –ö–į–ļ –ĺ—ā–ľ–Ķ—á–Ķ–Ĺ–ĺ –≤—č—ą–Ķ, –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤—É –ļ—É–Ī–ł—á–Ķ—Ā–ļ–ł—Ö –Ņ—Ä–ł–≤–Ķ–ī—Ď–Ĺ–Ĺ—č—Ö –ľ–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ–ĺ–≤ –ĺ–ī–Ĺ–ĺ–Ļ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ–Ļ –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ, –Ĺ–Ķ –ł–ľ–Ķ—é—Č–ł—Ö –ļ—Ä–į—ā–Ĺ—č—Ö –ļ–ĺ—Ä–Ĺ–Ķ–Ļ: –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ł —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É–Ķ—ā –ľ–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ
–ü–ĺ–ī–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –ľ–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ–ĺ–≤ –≤–ł–ī–į , –≥–ī–Ķ , —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ī–Ķ—Ą–ĺ—Ä–ľ–į—Ü–ł–ĺ–Ĺ–Ĺ—č–ľ —Ä–Ķ—ā—Ä–į–ļ—ā–ĺ–ľ –ĺ–Ī—ä–Ķ–ľ–Ľ—é—Č–Ķ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –ľ–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ–ĺ–≤. –ź –ł–ľ–Ķ–Ĺ–Ĺ–ĺ, –ł—Ā–ļ–ĺ–ľ–į—Ź –ī–Ķ—Ą–ĺ—Ä–ľ–į—Ü–ł—Ź –ľ–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ–ĺ–≤ –Ņ–Ķ—Ä–Ķ–Ĺ–ĺ—Ā–ł—ā —Ü–Ķ–Ĺ—ā—Ä –ľ–į—Ā—Ā –ł—Ö –ļ–ĺ—Ä–Ĺ–Ķ–Ļ –≤ –Ĺ–į—á–į–Ľ–ĺ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –ł –∑–į–ī–į—Ď—ā—Ā—Ź —Ą–ĺ—Ä–ľ—É–Ľ–ĺ–Ļ
–ú–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ –≤–ł–ī–į –Ĺ–Ķ –ł–ľ–Ķ–Ķ—ā –ļ—Ä–į—ā–Ĺ—č—Ö –ļ–ĺ—Ä–Ĺ–Ķ–Ļ —ā–ĺ–≥–ī–į –ł —ā–ĺ–Ľ—Ć–ļ–ĺ —ā–ĺ–≥–ī–į, –ļ–ĺ–≥–ī–į –Ķ–≥–ĺ –ī–ł—Ā–ļ—Ä–ł–ľ–ł–Ĺ–į–Ĺ—ā –Ĺ–Ķ —Ä–į–≤–Ķ–Ĺ –Ĺ—É–Ľ—é. –ü–ĺ—ć—ā–ĺ–ľ—É –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ —ā–į–ļ–ł—Ö –ľ–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ–ĺ–≤ –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ–ĺ –Ņ–ĺ–ī–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤—É –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į . –Ē–į–Ľ–Ķ–Ķ, –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ī–Ķ—Ą–ĺ—Ä–ľ–į—Ü–ł–ĺ–Ĺ–Ĺ—č–ľ —Ä–Ķ—ā—Ä–į–ļ—ā–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į . –ź –ł–ľ–Ķ–Ĺ–Ĺ–ĺ, –ł—Ā–ļ–ĺ–ľ–į—Ź —Ä–Ķ—ā—Ä–į–ļ—Ü–ł—Ź –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ ¬ę–Ņ–ĺ–ī–ļ—Ä—É—á–Ķ–Ŗŗɗ鬼 —Ä–į–ī–ł–į–Ľ—Ć–Ĺ—É—é –Ņ—Ä–ĺ–Ķ–ļ—Ü–ł—é –≤–ł–ī–į , –≥–ī–Ķ ‚ÄĒ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ–į—Ź –ļ–ĺ–Ĺ—Ā—ā–į–Ĺ—ā–į[17]. –ü–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –≤—č—Ā–Ķ–ļ–į–Ķ—ā –≤ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–Ļ —Ā—Ą–Ķ—Ä–Ķ —É–∑–Ķ–Ľ —ā—Ä–ł–Ľ–ł—Ā—ā–Ĺ–ł–ļ[18], –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ —Ā–ĺ–≤–Ņ–į–ī–į–Ķ—ā —Ā–ĺ –≤–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ–ĺ—Ā—ā—Ć—é –Ķ–≥–ĺ –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł—Ź. –°—Ą–Ķ—Ä—č  –ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć–ö–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –ī–ĺ–Ņ—É—Ā–ļ–į–Ķ—ā —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ķ –ĺ–Ņ–ł—Ā–į–Ĺ–ł–Ķ –≤ —ā–Ķ—Ä–ľ–ł–Ĺ–į—Ö –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–į. –í–≤–Ķ–ī—Ď–ľ –Ĺ–į –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č, –ĺ—ā–ĺ–∂–ī–Ķ—Ā—ā–≤–ł–≤ –Ķ—Ď —Ā–ĺ —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ĺ–ĺ–Ļ –Ķ–ī–ł–Ĺ–ł—á–Ĺ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć—é –Ĺ–į –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ–Ļ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł. –Ę–ĺ–≥–ī–į –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –ĺ—Ā—É—Č–Ķ—Ā—ā–≤–Ľ—Ź–Ķ—ā –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ . –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ —É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ—č—Ö –Ĺ–į–Ī–ĺ—Ä–ĺ–≤ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ–ĺ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—é –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –ł –ī–ł–∑—ä—é–Ĺ–ļ—ā–Ĺ–ĺ–≥–ĺ –ĺ–Ī—ä–Ķ–ī–ł–Ĺ–Ķ–Ĺ–ł—Ź –ļ–ĺ–Ņ–ł–Ļ –ĺ—ā–ļ—Ä—č—ā—č—Ö —Ā–ł–ľ–Ņ–Ľ–Ķ–ļ—Ā–ĺ–≤ —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł . –í —á–į—Ā—ā–Ĺ–ĺ—Ā—ā–ł, –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –≥–ĺ–ľ–ĺ—ā–ĺ–Ņ–ł—á–Ķ—Ā–ļ–ł —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ–ĺ –ī–ł–∑—ä—é–Ĺ–ļ—ā–Ĺ–ĺ–ľ—É –ĺ–Ī—ä–Ķ–ī–ł–Ĺ–Ķ–Ĺ–ł—é –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–Ķ–Ļ. –Ę–ĺ—á–Ĺ–Ķ–Ķ, –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ĺ —Ā–Ľ—É—á–į—é –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–į, –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–Ļ, —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ—č—Ö –≤ —Ą–ĺ—Ä–ľ–Ķ –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ľ–Ĺ–ĺ–≥–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į, —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ī–Ķ—Ą–ĺ—Ä–ľ–į—Ü–ł–ĺ–Ĺ–Ĺ—č–ľ —Ä–Ķ—ā—Ä–į–ļ—ā–ĺ–ľ –ĺ–Ī—ä–Ķ–ľ–Ľ—é—Č–Ķ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į. –ź–Ĺ–į–Ľ–ĺ–≥–ł—á–Ĺ—č–Ķ —Ä–į—Ā—Ā—É–∂–ī–Ķ–Ĺ–ł—Ź –Ņ–ĺ–ļ–į–∑—č–≤–į—é—ā, —á—ā–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–Ļ, —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ—č—Ö –≤ —Ą–ĺ—Ä–ľ–Ķ –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ľ–Ĺ–ĺ–≥–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į, —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ī–Ķ—Ą–ĺ—Ä–ľ–į—Ü–ł–ĺ–Ĺ–Ĺ—č–ľ —Ä–Ķ—ā—Ä–į–ļ—ā–ĺ–ľ –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į . –≠—ā–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ–ĺ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, –ł —ā–Ķ–ľ —Ā–į–ľ—č–ľ, –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –≥–ĺ–ľ–ĺ—ā–ĺ–Ņ–ł—á–Ķ—Ā–ļ–ł —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ–ĺ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł. –ü–į—Ä—č —ā–ĺ—á–Ķ–ļ –Ĺ–į —Ā—Ą–Ķ—Ä–į—Ö–ö–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –Ņ–į—Ä —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ –Ĺ–į –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ā–ĺ–≤–Ņ–į–ī–į–Ķ—ā —Ā –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł–Ķ–ľ –Ņ—Ä–ĺ—Ā—ā–ĺ–Ļ –∑–į–ľ–ļ–Ĺ—É—ā–ĺ–Ļ –ļ—Ä–ł–≤–ĺ–Ļ –ī–ĺ —ā–ĺ—Ä–į . –ė–ľ–Ķ–Ķ—ā—Ā—Ź —ā–į–ļ–∂–Ķ —Ā–Ľ–Ķ–ī—É—é—Č–į—Ź –Ĺ–į–≥–Ľ—Ź–ī–Ĺ–į—Ź –ļ–ĺ–ī–ł—Ä–ĺ–≤–ļ–į —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ĺ–≤ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į . –Ē–Ľ—Ź —Ā—ā–Ķ—Ä–Ķ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–į—Ź –Ņ—Ä–ĺ–Ķ–ļ—Ü–ł—Ź –ĺ—Ā—É—Č–Ķ—Ā—ā–≤–Ľ—Ź–Ķ—ā –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ . –Ę–ĺ—á–Ĺ–Ķ–Ķ, –≤ —Ā–Ľ—É—á–į–Ķ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ —Ā–ĺ–Ņ–ĺ—Ā—ā–į–≤–ł—ā—Ć —ā–ĺ—á–ļ–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—É –Ĺ–į –ī—É–≥–Ķ , –Ņ—Ä–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ–ĺ–Ļ –≤ –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–ľ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–ł –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł. –Ē–į–Ĺ–Ĺ–į—Ź –ļ–ĺ–ī–ł—Ä–ĺ–≤–ļ–į –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ–į –ł —É—Ā—ā–į–Ĺ–į–≤–Ľ–ł–≤–į–Ķ—ā –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –Ņ–į—Ä —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ –Ĺ–į –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ā –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ—č–ľ —Ü–ł–Ľ–ł–Ĺ–ī—Ä–ĺ–ľ. –Ē–į–Ĺ–Ĺ—č–Ļ –Ņ–ĺ–ī—Ö–ĺ–ī —á–į—Ā—ā–ł—á–Ĺ–ĺ –ĺ–Ī–ĺ–Ī—Č–į–Ķ—ā—Ā—Ź –Ĺ–į –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ—É—é —Ā—Ą–Ķ—Ä—É . –Ē–Ľ—Ź —Ā—ā–Ķ—Ä–Ķ–ĺ–≥—Ä–į—Ą–ł—á–Ķ—Ā–ļ–į—Ź –Ņ—Ä–ĺ–Ķ–ļ—Ü–ł—Ź –ĺ—Ā—É—Č–Ķ—Ā—ā–≤–Ľ—Ź–Ķ—ā –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ . –ě–ī–Ĺ–į–ļ–ĺ –≤ –ĺ–Ī—Č–Ķ–ľ —Ā–Ľ—É—á–į–Ķ –ľ–ĺ–∂–Ķ—ā –Ĺ–Ķ –Ī—č—ā—Ć –Ķ—Ā—ā–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —Ā–Ņ–ĺ—Ā–ĺ–Ī–į —Ā–ĺ–Ņ–ĺ—Ā—ā–į–≤–ł—ā—Ć –Ņ–ĺ–ī–ĺ–Ī–Ĺ—É—é –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—É –ļ–į–∂–ī–ĺ–Ļ —ā–ĺ—á–ļ–Ķ —ā–į–ļ, —á—ā–ĺ–Ī—č –ļ–ĺ–ī–ł—Ä–ĺ–≤–ļ–į –ĺ—Ā—É—Č–Ķ—Ā—ā–≤–Ľ—Ź–Ľ–į –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤ –ł . –í –ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł, –ĺ–Ĺ–į –ĺ—Ā—É—Č–Ķ—Ā—ā–≤–Ľ—Ź–Ķ—ā –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ –ľ–Ķ–∂–ī—É –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ—č–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ–ľ –Ņ–į—Ä —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ –Ĺ–į —Ā—Ą–Ķ—Ä–Ķ –ł –Ķ–≥–ĺ –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ—č–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ–ľ —Ā—Ą–Ķ—Ä—č . –ö—Ä–ĺ–ľ–Ķ —ā–ĺ–≥–ĺ, –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ
–∑–į–ī–į–Ĺ–Ĺ–ĺ–Ķ —Ą–ĺ—Ä–ľ—É–Ľ–ĺ–Ļ , —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≥–ĺ–ľ–ĺ—ā–ĺ–Ņ–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ–ĺ—Ā—ā—Ć—é[19]. –ü—Ä–Ķ–Ņ—Ź—ā—Ā—ā–≤–ł–Ķ–ľ –ļ –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ–ĺ—Ā—ā–ł –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤ –ł —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ĺ–Ķ–Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ł–∑—É–Ķ–ľ–ĺ—Ā—ā—Ć —Ā—Ą–Ķ—Ä—č , –ł–ľ–Ķ—é—Č–į—Ź –ľ–Ķ—Ā—ā–ĺ –Ņ—Ä–ł .  –ö–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –ī–≤—É—Ö—ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–Ĺ—č—Ö –Ņ–ĺ–ī–ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–ĺ –ł–∑ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ. –ü—Ä–Ķ–ī—Ā—ā–į–≤–ł–ľ —ā–ĺ—Ä –≤ –≤–ł–ī–Ķ —Ą–į–ļ—ā–ĺ—Ä–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –ļ–≤–į–ī—Ä–į—ā–į –Ņ–ĺ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—é –ł , –≥–ī–Ķ . –Ę–ĺ–≥–ī–į –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –Ņ–ĺ–Ľ—É—á–į–Ķ—ā—Ā—Ź –ł–∑ –ī–į–Ĺ–Ĺ–ĺ–≥–ĺ —Ą–į–ļ—ā–ĺ—Ä–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į —É–ī–į–Ľ–Ķ–Ĺ–ł–Ķ–ľ –ī–ł–į–≥–ĺ–Ĺ–į–Ľ–ł . –ß—ā–ĺ–Ī—č –Ņ–ĺ–Ľ—É—á–ł—ā—Ć –ł—Ā–ļ–ĺ–ľ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ , —ā—Ä–Ķ–Ī—É–Ķ—ā—Ā—Ź –ĺ—ā–ĺ–∂–ī–Ķ—Ā—ā–≤–ł—ā—Ć —ā–ĺ—á–ļ–ł –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į, —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ĺ—č–Ķ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ī–į–Ĺ–Ĺ–ĺ–Ļ –ī–ł–į–≥–ĺ–Ĺ–į–Ľ–ł: . –ü–ĺ–ī–ĺ–Ī–Ĺ–ĺ–Ķ –ĺ—ā–ĺ–∂–ī–Ķ—Ā—ā–≤–Ľ–Ķ–Ĺ–ł–Ķ —Ä–į–≤–Ĺ–ĺ—Ā–ł–Ľ—Ć–Ĺ–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł—é –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –≤ –≤–ł–ī–Ķ —Ą–į–ļ—ā–ĺ—Ä–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į —Ā –≤—č—Ä–Ķ–∑–į–Ĺ–Ĺ–ĺ–Ļ –≥–ł–Ņ–ĺ—ā–Ķ–Ĺ—É–∑–ĺ–Ļ –Ņ–ĺ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—é , –≥–ī–Ķ . –Ę–į–ļ–ĺ–Ķ —Ą–į–ļ—ā–ĺ—Ä–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ–ĺ –≤–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ–ĺ—Ā—ā–ł –Ľ–Ķ–Ĺ—ā—č –ú—Ď–Ī–ł—É—Ā–į.  –í –ĺ–Ī—Č–Ķ–ľ —Ā–Ľ—É—á–į–Ķ —Ā—Ą–Ķ—Ä—č –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –ī–ĺ–Ņ—É—Ā–ļ–į–Ķ—ā —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ķ –ĺ–Ņ–ł—Ā–į–Ĺ–ł–Ķ. –ü–ĺ–ī–ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ —ć—ā–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į, —Ā–ĺ—Ā—ā–ĺ—Ź—Č–Ķ–Ķ –ł–∑ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ĺ–≤ –≤–ł–ī–į , –≥–ī–Ķ , –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ–ĺ –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–ľ—É –Ņ—Ä–ĺ–Ķ–ļ—ā–ł–≤–Ĺ–ĺ–ľ—É –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤—É : –Ņ–į—Ä–Ķ –ī–ł–į–ľ–Ķ—ā—Ä–į–Ľ—Ć–Ĺ–ĺ –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ –Ĺ–į —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É–Ķ—ā –Ņ—Ä—Ź–ľ–į—Ź –≤ . –Ē–į–Ĺ–Ĺ–ĺ–Ķ –Ņ–ĺ–ī–ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ī–Ķ—Ą–ĺ—Ä–ľ–į—Ü–ł–ĺ–Ĺ–Ĺ—č–ľ —Ä–Ķ—ā—Ä–į–ļ—ā–ĺ–ľ –ĺ–Ī—ä–Ķ–ľ–Ľ—é—Č–Ķ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į : –ļ–į–∂–ī–į—Ź –Ĺ–Ķ–į–Ĺ—ā–ł–Ņ–ĺ–ī–į–Ľ—Ć–Ĺ–į—Ź –Ņ–į—Ä–į –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć —Ä–į–≤–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ –ī–Ķ—Ą–ĺ—Ä–ľ–ł—Ä–ĺ–≤–į–Ĺ–į –≤ –į–Ĺ—ā–ł–Ņ–ĺ–ī–į–Ľ—Ć–Ĺ—É—é –Ņ—É—ā—Ď–ľ —Ä–į—Ā—ā–į–Ľ–ļ–ł–≤–į–Ĺ–ł—Ź —ā–ĺ—á–Ķ–ļ –ł –≤–ī–ĺ–Ľ—Ć –Ķ–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–Ļ —Ā–ĺ–ī–Ķ—Ä–∂–į—Č–Ķ–Ļ –ł—Ö –Ī–ĺ–Ľ—Ć—ą–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ā—Ą–Ķ—Ä—č . –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –≤ —Ā–Ľ—É—á–į–Ķ –ł—Ā–ļ–ĺ–ľ–ĺ–Ķ –Ņ—Ä–ĺ–Ķ–ļ—ā–ł–≤–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –≤–ļ–Ľ–į–ī—č–≤–į–Ķ—ā—Ā—Ź –Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–ĺ–ľ –≤—č—ą–Ķ–ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–≥–ĺ –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ–į –≤–ĺ –≤–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ–ĺ—Ā—ā—Ć –Ľ–Ķ–Ĺ—ā—č –ú—Ď–Ī–ł—É—Ā–į –≤ –≤–ł–ī–Ķ –Ķ—Ď —Ā–Ķ—Ä–ī—Ü–Ķ–≤–ł–Ĺ—č (–ł–Ľ–ł —Ā—Ä–Ķ–ī–Ĺ–Ķ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł), –į –ī–Ķ—Ą–ĺ—Ä–ľ–į—Ü–ł–ĺ–Ĺ–Ĺ–į—Ź —Ä–Ķ—ā—Ä–į–ļ—Ü–ł—Ź —Ā—ā—Ź–≥–ł–≤–į–Ķ—ā –ļ–į–∂–ī—č–Ļ –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—č–Ļ —Ā–Ķ—Ä–ī—Ü–Ķ–≤–ł–Ĺ–Ķ –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ –Ľ–Ķ–Ĺ—ā—č –ú—Ď–Ī–ł—É—Ā–į –≤ —ā–ĺ—á–ļ—É. –°–į–ľ–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ–ĺ —ā–ĺ—ā–į–Ľ—Ć–Ĺ–ĺ–ľ—É –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤—É -–ľ–Ķ—Ä–Ĺ–ĺ–≥–ĺ –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ĺ–≥–ĺ —Ä–į—Ā—Ā–Ľ–ĺ–Ķ–Ĺ–ł—Ź –Ĺ–į–ī , –≥–ī–Ķ —Ā–ł–ľ–≤–ĺ–Ľ –ĺ–Ī–ĺ–∑–Ĺ–į—á–į–Ķ—ā –ĺ–ī–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ–Ķ —ā–į–≤—ā–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–Ķ —Ä–į—Ā—Ā–Ľ–ĺ–Ķ–Ĺ–ł–Ķ –Ĺ–į–ī , –į —Ā–ł–ľ–≤–ĺ–Ľ ‚ÄĒ –Ķ–≥–ĺ –ĺ—Ä—ā–ĺ–≥–ĺ–Ĺ–į–Ľ—Ć–Ĺ–ĺ–Ķ –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł–Ķ[20]. –Ę—Ä–ĺ–Ļ–ļ–ł —ā–ĺ—á–Ķ–ļ –Ĺ–į —Ā—Ą–Ķ—Ä–į—Ö–ö–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –ī–ĺ–Ņ—É—Ā–ļ–į–Ķ—ā —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ķ –ĺ–Ņ–ł—Ā–į–Ĺ–ł–Ķ. –ě—ā–ĺ–∂–ī–Ķ—Ā—ā–≤–ł–ľ —Ā—Ą–Ķ—Ä—É —Ā –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ—č–ľ –Ņ—Ä–ĺ–Ķ–ļ—ā–ł–≤–Ĺ—č–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ–ľ[–į–Ĺ–≥–Ľ.] —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł –ĺ–ī–ł–Ĺ, —ā–ĺ –Ķ—Ā—ā—Ć —Ā–ĺ —Ā—Ą–Ķ—Ä–ĺ–Ļ –†–ł–ľ–į–Ĺ–į . –Ę–ĺ–≥–ī–į –ī–Ľ—Ź –Ľ—é–Ī–ĺ–Ļ —ā—Ä–ĺ–Ļ–ļ–ł –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ —É—Ā—ā–į–Ĺ–į–≤–Ľ–ł–≤–į–Ķ—ā –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ –ľ–Ķ–∂–ī—É –Ņ—Ä–ĺ–Ķ–ļ—ā–ł–≤–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–ĺ–Ļ –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł–Ļ –ú—Ď–Ī–ł—É—Ā–į –ł –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ—č–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ–ľ —ā—Ä–ĺ–Ķ–ļ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ —Ā—Ą–Ķ—Ä—č[21]. –í –ĺ–Ī—Č–Ķ–ľ —Ā–Ľ—É—á–į–Ķ –ī–Ľ—Ź –Ľ—é–Ī–ĺ–Ļ —ā—Ä–ĺ–Ļ–ļ–ł –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ —É—Ā—ā–į–Ĺ–į–≤–Ľ–ł–≤–į–Ķ—ā –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ[19][22]
–ü—Ä–ĺ–Ķ–ļ—ā–ł–≤–Ĺ–į—Ź —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ–į—Ź —É–Ĺ–ł—ā–į—Ä–Ĺ–į—Ź –≥—Ä—É–Ņ–Ņ–į[–į–Ĺ–≥–Ľ.] —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ľ–į–ļ—Ā–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–Ļ –ļ–ĺ–ľ–Ņ–į–ļ—ā–Ĺ–ĺ–Ļ –Ņ–ĺ–ī–≥—Ä—É–Ņ–Ņ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ—č –ł, —Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, –Ķ—Ď –ī–Ķ—Ą–ĺ—Ä–ľ–į—Ü–ł–ĺ–Ĺ–Ĺ—č–ľ —Ä–Ķ—ā—Ä–į–ļ—ā–ĺ–ľ[19]. –ü–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É –ĺ–Ĺ–į –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ–į —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ–ĺ–Ļ –ĺ—Ä—ā–ĺ–≥–ĺ–Ĺ–į–Ľ—Ć–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–Ķ –ł –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ–į —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ—É –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–ľ—É –Ņ—Ä–ĺ–Ķ–ļ—ā–ł–≤–Ĺ–ĺ–ľ—É –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤—É , –ľ–ĺ–∂–Ĺ–ĺ –∑–į–ļ–Ľ—é—á–ł—ā—Ć, —á—ā–ĺ –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –≥–ĺ–ľ–ĺ—ā–ĺ–Ņ–ł—á–Ķ—Ā–ļ–ł —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ–ĺ –ī–į–Ĺ–Ĺ—č–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į–ľ[23]. –ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ—Ź—Ź –≥–ĺ–ľ–ĺ—ā–ĺ–Ņ–ł—á–Ķ—Ā–ļ–į—Ź —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ–ĺ—Ā—ā—Ć —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ –ĺ–Ī–ĺ–Ī—Č–į–Ķ—ā—Ā—Ź –Ĺ–į –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ—É—é —Ā—Ą–Ķ—Ä—É [24]. –ě—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –∑–į–ī–į—Ď—ā –≤–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –Ķ–ī–ł–Ĺ–ł—á–Ĺ—č—Ö –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –≤–Ķ–ļ—ā–ĺ—Ä–ĺ–≤[–į–Ĺ–≥–Ľ.] —Ā—Ą–Ķ—Ä—č –≤ –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ, –≥–ī–Ķ —Ā–ł–ľ–≤–ĺ–Ľ –ĺ–Ī–ĺ–∑–Ĺ–į—á–į–Ķ—ā —ć–ļ—Ā–Ņ–ĺ–Ĺ–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ–ĺ–Ķ –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ. –ě–Ī—Ä–į–∑ —ć—ā–ĺ–≥–ĺ –≤–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ī–Ķ—Ą–ĺ—Ä–ľ–į—Ü–ł–ĺ–Ĺ–Ĺ—č–ľ —Ä–Ķ—ā—Ä–į–ļ—ā–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į [19]. –ü—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ–ĺ –ľ–Ĺ–ĺ–≥–ĺ–ĺ–Ī—Ä–į–∑–ł—é –®—ā–ł—Ą–Ķ–Ľ—Ź[–į–Ĺ–≥–Ľ.] –ĺ—Ä—ā–ĺ–Ĺ–ĺ—Ä–ľ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—č—Ö -—Ä–Ķ–Ņ–Ķ—Ä–ĺ–≤ –≤ . –í —Ā–Ľ—É—á–į–Ķ –ł–ľ–Ķ–Ķ—ā—Ā—Ź –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ . –†–ĺ–Ľ—Ć –≤ —ā–Ķ–ĺ—Ä–ł–ł –ļ–ĺ—Ā –ö–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ—č–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź—é—ā —Ā–ĺ–Ī–ĺ–Ļ –Ķ—Ā—ā–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—É—é —Ā—Ä–Ķ–ī—É –ī–Ľ—Ź –ł–∑—É—á–Ķ–Ĺ–ł—Ź –ł —Ä–į–∑–≤–ł—ā–ł—Ź —ā–Ķ–ĺ—Ä–ł–ł –ļ–ĺ—Ā. –°–≤—Ź–∑—Ć —Ā –ļ–ĺ—Ā–į–ľ–ł —Ā–ĺ—Ā—ā–ĺ–ł—ā –≤ —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–ľ[25]. –ü—É—Ā—ā—Ć ‚ÄĒ —Ā–ĺ–≤–ĺ–ļ—É–Ņ–Ĺ–ĺ—Ā—ā—Ć –ł–∑ –Ņ—É—ā–Ķ–Ļ –Ņ–ĺ–Ņ–į—Ä–Ĺ–ĺ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö –≤ –ļ–į–∂–ī—č–Ļ –ľ–ĺ–ľ–Ķ–Ĺ—ā –≤—Ä–Ķ–ľ–Ķ–Ĺ–ł —ā–ĺ—á–Ķ–ļ –≤ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ , —ā–ĺ –Ķ—Ā—ā—Ć –Ņ—É—ā–Ķ–Ļ, –ī–Ľ—Ź –ļ–ĺ—ā–ĺ—Ä—č—Ö –≤—č–Ņ–ĺ–Ľ–Ĺ—Ź—é—ā—Ā—Ź —É—Ā–Ľ–ĺ–≤–ł—Ź –Ņ—Ä–ł –≤—Ā–Ķ—Ö –ł . –Ę–į–ļ–į—Ź —Ā–ĺ–≤–ĺ–ļ—É–Ņ–Ĺ–ĺ—Ā—ā—Ć –Ķ—Ā—ā–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ –∑–į–ī–į—Ď—ā –Ņ—É—ā—Ć –≤ –ļ–į–∂–ī–ĺ–ľ –ł–∑ –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ—č—Ö –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤ –ł , –ł–Ľ–ł, –ł–Ĺ—č–ľ–ł —Ā–Ľ–ĺ–≤–į–ľ–ł, –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ–ĺ–Ķ —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–ĺ –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–Ļ —ā–ĺ—á–Ķ–ļ –≤ . –ó–į–ī–į–Ĺ–Ĺ—č–Ļ —ā–į–ļ –Ņ—É—ā—Ć –∑–į–ľ–ļ–Ĺ—É—ā, —ā–ĺ –Ķ—Ā—ā—Ć —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–Ķ—ā–Ľ–Ķ–Ļ, –Ķ—Ā–Ľ–ł –Ķ–≥–ĺ –ļ–ĺ–Ĺ–Ķ—á–Ĺ–į—Ź –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł—Ź —Ā–ĺ–≤–Ņ–į–ī–į–Ķ—ā —Ā –Ĺ–į—á–į–Ľ—Ć–Ĺ–ĺ–Ļ. –í —Ā–Ľ—É—á–į–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į —ć—ā–ĺ –ĺ–∑–Ĺ–į—á–į–Ķ—ā —Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–ĺ —ā–ĺ—á–Ķ–ļ –ī–Ľ—Ź –≤—Ā–Ķ—Ö , –į –≤ —Ā–Ľ—É—á–į–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į ‚ÄĒ —Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤
–ü—É—Ā—ā—Ć —ā–Ķ–Ņ–Ķ—Ä—Ć . –ē—Ā–Ľ–ł –Ņ–ĺ–ī–ĺ–Ī–Ĺ–į—Ź —Ā–ĺ–≤–ĺ–ļ—É–Ņ–Ĺ–ĺ—Ā—ā—Ć –Ņ—É—ā–Ķ–Ļ –∑–į–ī–į—Ď—ā –Ņ–Ķ—ā–Ľ—é –≤ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ , —ā–ĺ –ĺ–Ĺ–į –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā –Ĺ–į–Ī–ĺ—Ä –ļ—Ä–ł–≤—č—Ö
–∑–į–ī–į–Ĺ–Ĺ—č–Ļ —Ą–ĺ—Ä–ľ—É–Ľ–ĺ–Ļ , –ļ–ĺ—ā–ĺ—Ä—č–Ļ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ—É—é –ļ–ĺ—Ā—É –ł–∑ –Ĺ–ł—ā–Ķ–Ļ. –ź –Ķ—Ā–Ľ–ł –Ņ—É—ā–ł –∑–į–ī–į—é—ā –Ņ–Ķ—ā–Ľ—é –≤ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ , —ā–ĺ –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ–į—Ź –ļ–ĺ—Ā–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ļ—Ä–į—ą–Ķ–Ĺ–ĺ–Ļ, —ā–ĺ –Ķ—Ā—ā—Ć –ļ–ĺ–Ĺ–Ķ—Ü –ļ–į–∂–ī–ĺ–Ļ –Ķ—Ď –Ĺ–ł—ā–ł –Ĺ–į—Ö–ĺ–ī–ł—ā—Ā—Ź –Ĺ–į —ā–ĺ–ľ –∂–Ķ —É—Ä–ĺ–≤–Ĺ–Ķ, —á—ā–ĺ –ł –Ĺ–į—á–į–Ľ–ĺ. –í –ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł —Ą—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ—Ć–Ĺ–į—Ź –≥—Ä—É–Ņ–Ņ–į –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –Ĺ–Ķ—É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ—č—Ö –Ĺ–į–Ī–ĺ—Ä–ĺ–≤ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ –ł–∑–ĺ–ľ–ĺ—Ä—Ą–Ĺ–į –≥—Ä—É–Ņ–Ņ–Ķ –ļ–ĺ—Ā [9], –į —Ą—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ—Ć–Ĺ–į—Ź –≥—Ä—É–Ņ–Ņ–į –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į —É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ—č—Ö –Ĺ–į–Ī–ĺ—Ä–ĺ–≤ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ –ł–∑–ĺ–ľ–ĺ—Ä—Ą–Ĺ–į –≥—Ä—É–Ņ–Ņ–Ķ –ļ—Ä–į—ą–Ķ–Ĺ—č—Ö –ļ–ĺ—Ā [25]. –ď—Ä—É–Ņ–Ņ–į –ļ–ĺ—Ā —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į–ď—Ä—É–Ņ–Ņ–ĺ–Ļ –ļ–ĺ—Ā –ł –≥—Ä—É–Ņ–Ņ–ĺ–Ļ –ļ—Ä–į—ą–Ķ–Ĺ—č—Ö –ļ–ĺ—Ā –ł–∑ –Ĺ–ł—ā–Ķ–Ļ —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –Ĺ–į–∑—č–≤–į—é—ā—Ā—Ź[6], —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ, –≥—Ä—É–Ņ–Ņ—č
–Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, —ā–į–ļ –ļ–į–ļ
–ł–ľ–Ķ—é—ā—Ā—Ź —Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–į
–ė–Ĺ—č–ľ–ł —Ā–Ľ–ĺ–≤–į–ľ–ł, –≥—Ä—É–Ņ–Ņ—č –ļ–ĺ—Ā –ĺ–Ī–ĺ–Ī—Č–į—é—ā —Ą—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ—Ć–Ĺ—É—é –≥—Ä—É–Ņ–Ņ—É. –ö—Ä–ĺ–ľ–Ķ —ā–ĺ–≥–ĺ, –≥—Ä—É–Ņ–Ņ—č –ļ–ĺ—Ā –Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā–Ķ–Ļ —ā–Ķ—Ā–Ĺ–ĺ —Ā–≤—Ź–∑–į–Ĺ—č —Ā –ł—Ö –≥—Ä—É–Ņ–Ņ–į–ľ–ł –ļ–Ľ–į—Ā—Ā–ĺ–≤ –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ļ. –ö–į–∂–ī–ĺ–ľ—É —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā—É –ľ–ĺ–∂–Ĺ–ĺ —Ā–ĺ–Ņ–ĺ—Ā—ā–į–≤–ł—ā—Ć —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ—č, –į –ł–ľ–Ķ–Ĺ–Ĺ–ĺ, –Ņ–Ķ—Ä–Ķ—Ā—ā–į–Ĺ–ĺ–≤–ļ—É –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–Ķ–≥–ĺ —É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –ļ–ĺ—Ä—ā–Ķ–∂–į. –ė–Ĺ—č–ľ–ł —Ā–Ľ–ĺ–≤–į–ľ–ł, —ć—ā–į –Ņ–Ķ—Ä–Ķ—Ā—ā–į–Ĺ–ĺ–≤–ļ–į –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź –Ľ–ł—Ā—ā–ĺ–ľ, —Ā–ĺ–ī–Ķ—Ä–∂–į—Č–Ķ–ľ –ļ–ĺ–Ĺ–Ķ—Ü –Ņ–ĺ–ī–Ĺ—Ź—ā–ł—Ź –Ņ–Ķ—ā–Ľ–ł –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ĺ–į–ļ—Ä—č—ā–ł—Ź
–§—É–Ĺ–ļ—Ü–ł—Ź —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≥–ĺ–ľ–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ–ĺ–ľ –ł –∑–į–ī–į—Ď—ā –ļ–ĺ—Ä–ĺ—ā–ļ—É—é —ā–ĺ—á–Ĺ—É—é –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā—Ć
–ü—Ä–ł–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź–≠–Ľ–Ķ–ļ—ā—Ä–ĺ—Ā—ā–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ–ö–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ—č–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ—č –ī–Ľ—Ź –≥–ĺ–ľ–ĺ—ā–ĺ–Ņ–ł—á–Ķ—Ā–ļ–ĺ–Ļ –į–Ņ–Ņ—Ä–ĺ–ļ—Ā–ł–ľ–į—Ü–ł–ł –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į —Ā–ĺ—Ö—Ä–į–Ĺ—Ź—é—Č–ł—Ö –ĺ—ā–ľ–Ķ—á–Ķ–Ĺ–Ĺ—č–Ķ —ā–ĺ—á–ļ–ł –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ—č—Ö –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ļ —Ā—Ą–Ķ—Ä—č –≤ —Ā–Ķ–Ī—Ź, —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į–Ķ–ľ–ĺ–≥–ĺ —Ā –ļ–ĺ–ľ–Ņ–į–ļ—ā–Ĺ–ĺ-–ĺ—ā–ļ—Ä—č—ā–ĺ–Ļ —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł–Ķ–Ļ. –ė–Ĺ—ā–Ķ—Ä–Ķ—Ā –ļ –ł–∑—É—á–Ķ–Ĺ–ł—é –≥–ĺ–ľ–ĺ—ā–ĺ–Ņ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —ā–ł–Ņ–į –ī–į–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –≤—č–∑–≤–į–Ĺ —ā–Ķ–ľ, —á—ā–ĺ, —Ā–ĺ–≥–Ľ–į—Ā–Ĺ–ĺ –ī–≤–ĺ–Ļ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ—Ā—ā–ł –≠–ļ–ľ–į–Ĺ–Ĺ–į ‚ÄĒ –•–ł–Ľ—ā–ĺ–Ĺ–į[–į–Ĺ–≥–Ľ.], –ĺ–Ĺ–ĺ –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ–ĺ —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–ľ—É –ł—ā–Ķ—Ä–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–ľ—É –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤—É –Ņ–Ķ—ā–Ķ–Ľ—Ć:
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –Ķ–≥–ĺ –≥–ĺ–ľ–ĺ—ā–ĺ–Ņ–ł—á–Ķ—Ā–ļ–ł–Ķ –≥—Ä—É–Ņ–Ņ—č –ł–∑–ĺ–ľ–ĺ—Ä—Ą–Ĺ—č –≥–ĺ–ľ–ĺ—ā–ĺ–Ņ–ł—á–Ķ—Ā–ļ–ł–ľ –≥—Ä—É–Ņ–Ņ–į–ľ —Ā—Ą–Ķ—Ä—č :
–ö–Ľ–į—Ā—Ā–ł—á–Ķ—Ā–ļ–ł–Ļ –Ņ–ĺ–ī—Ö–ĺ–ī –ļ –į–Ņ–Ņ—Ä–ĺ–ļ—Ā–ł–ľ–į—Ü–ł–ł —Ā–ĺ—Ā—ā–ĺ–ł—ā –≤ —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–ľ[26]. 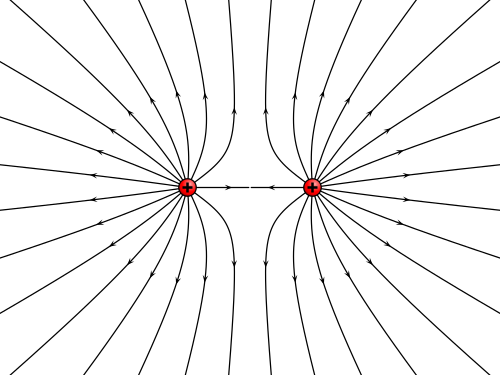 –°–ĺ–Ņ–ĺ—Ā—ā–į–≤–ł–ľ –ļ–į–∂–ī–ĺ–ľ—É –ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–ľ—É –Ņ–ĺ–ī–ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤—É –ł–∑ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ĺ–≤ —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ķ –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ–ĺ–Ķ –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –ł–∑ —Ā—Ą–Ķ—Ä—č –≤ —Ā–Ķ–Ī—Ź. –ü—É—Ā—ā—Ć ‚ÄĒ –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ĺ–Ķ –Ņ–ĺ–Ľ–Ķ, –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź—é—Č–Ķ–Ķ —Ā–ĺ–Ī–ĺ–Ļ —ć–Ľ–Ķ–ļ—ā—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ķ –Ņ–ĺ–Ľ–Ķ, –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ–ĺ–Ķ –Ņ—É—ā—Ď–ľ —Ä–į–∑–ľ–Ķ—Č–Ķ–Ĺ–ł—Ź –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –∑–į—Ä—Ź–∂–Ķ–Ĺ–Ĺ–ĺ–Ļ —á–į—Ā—ā–ł—Ü—č –≤ –ļ–į–∂–ī—É—é —ā–ĺ—á–ļ—É . –Ē–į–Ĺ–Ĺ–ĺ–Ķ –≤–Ķ–ļ—ā–ĺ—Ä–Ĺ–ĺ–Ķ –Ņ–ĺ–Ľ–Ķ –ľ–ĺ–∂–Ĺ–ĺ –ī–ĺ–ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā—Ć –ī–ĺ –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ–ĺ–≥–ĺ –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł—Ź –ĺ–ī–Ĺ–ĺ—ā–ĺ—á–Ķ—á–Ĺ—č—Ö –ļ–ĺ–ľ–Ņ–į–ļ—ā–ł—Ą–ł–ļ–į—Ü–ł–Ļ –Ņ—Ä–į–≤–ł–Ľ–į–ľ–ł –ł , –≥–ī–Ķ . –ö–ĺ–ľ–Ņ–ĺ–∑–ł—Ü–ł—Ź —Ā –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ–ĺ–ľ –∑–į–ī–į—Ď—ā –ł—Ā–ļ–ĺ–ľ–ĺ–Ķ –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ–ĺ–Ķ –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –ł–∑ —Ā—Ą–Ķ—Ä—č –≤ —Ā–Ķ–Ī—Ź. –ē–≥–ĺ —Ā—ā–Ķ–Ņ–Ķ–Ĺ—Ć —Ä–į–≤–Ĺ–į . –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ –∑–į–ī–į–Ĺ–Ĺ–ĺ–Ķ —Ā–ĺ–Ņ–ĺ—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ–ĺ–Ķ –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –ł–∑ –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –Ĺ–Ķ—É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ—č—Ö –Ĺ–į–Ī–ĺ—Ä–ĺ–≤ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —ā–ĺ—á–Ķ–ļ –≤ –Ņ–ĺ–ī–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ—č—Ö –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ļ , —Ā–ĺ—Ā—ā–ĺ—Ź—Č–Ķ–Ķ –ł–∑ –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ļ —Ā—ā–Ķ–Ņ–Ķ–Ĺ–ł , –Ņ–Ķ—Ä–Ķ–≤–ĺ–ī—Ź—Č–ł—Ö –ĺ—ā–ľ–Ķ—á–Ķ–Ĺ–Ĺ—É—é —ā–ĺ—á–ļ—É —Ā–Ľ–Ķ–≤–į –≤ –ĺ—ā–ľ–Ķ—á–Ķ–Ĺ–Ĺ—É—é —ā–ĺ—á–ļ—É —Ā–Ņ—Ä–į–≤–į. –ě–Ĺ–ĺ –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź —ć–Ľ–Ķ–ļ—ā—Ä–ĺ—Ā—ā–į—ā–ł—á–Ķ—Ā–ļ–ł–ľ –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ–ľ[27] –ł –∑–į–ī–į—Ď—ā –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –ł–∑ –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –ļ–ĺ–Ĺ–Ķ—á–Ĺ—č—Ö –Ņ–ĺ–ī–ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤. –≠–Ľ–Ķ–ļ—ā—Ä–ĺ—Ā—ā–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā—Ā—Ź –ī–Ľ—Ź –≥–ĺ–ľ–ĺ—ā–ĺ–Ņ–ł—á–Ķ—Ā–ļ–ĺ–Ļ –į–Ņ–Ņ—Ä–ĺ–ļ—Ā–ł–ľ–į—Ü–ł–ł –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į . –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –≤ –Ņ—Ä–ĺ—Ā—ā–Ķ–Ļ—ą–Ķ–ľ —Ā–Ľ—É—á–į–Ķ –ĺ–Ĺ–ĺ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ā–Ľ–į–Ī–ĺ–Ļ –≥–ĺ–ľ–ĺ—ā–ĺ–Ņ–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ–ĺ—Ā—ā—Ć—é. –Ę–ĺ—á–Ĺ–Ķ–Ķ, –ļ–į–∂–ī–į—Ź –ļ–ĺ–ľ–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā–į –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į —Ā—ā—Ź–≥–ł–≤–į–Ķ–ľ–į: –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ļ –≤–ł–ī–į , –≥–ī–Ķ , —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ķ–≥–ĺ –ī–Ķ—Ą–ĺ—Ä–ľ–į—Ü–ł–ĺ–Ĺ–Ĺ—č–ľ —Ä–Ķ—ā—Ä–į–ļ—ā–ĺ–ľ[28]. –ü—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ —ā–į–ļ–∂–Ķ —Ā—ā—Ź–≥–ł–≤–į–Ķ–ľ–ĺ –ł –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ–ĺ –≤–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ–ĺ—Ā—ā–ł —Ā–ł–ľ–Ņ–Ľ–Ķ–ļ—Ā–į —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł . –í –ĺ–Ī—Č–Ķ–ľ —Ā–Ľ—É—á–į–Ķ –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –ł–Ĺ–ī—É—Ü–ł—Ä—É–Ķ—ā –ł–∑–ĺ–ľ–ĺ—Ä—Ą–ł–∑–ľ –≥—Ä—É–Ņ–Ņ –≥–ĺ–ľ–ĺ–Ľ–ĺ–≥–ł–Ļ –≤ —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł [28]. –í —Ā–Ľ—É—á–į–Ķ –ī–į–Ĺ–Ĺ—č–Ļ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā —Ā–≤–ł–ī–Ķ—ā–Ķ–Ľ—Ć—Ā—ā–≤—É–Ķ—ā –ĺ —Ā–≤—Ź–∑–ł –ľ–Ķ–∂–ī—É –≥–ĺ–ľ–ĺ—ā–ĺ–Ņ–ł—á–Ķ—Ā–ļ–ł–ľ–ł —Ā–≤–ĺ–Ļ—Ā—ā–≤–į–ľ–ł –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ—č—Ö –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤ –ł –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į . –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –ĺ–Ĺ –Ņ—Ä–Ķ–ī–ĺ—Ā—ā–į–≤–Ľ—Ź–Ķ—ā –Ņ–ĺ–ī—Ö–ĺ–ī –ļ –≤—č—á–ł—Ā–Ľ–Ķ–Ĺ–ł—é –≥—Ä—É–Ņ–Ņ—č
–ü–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –į—Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–ľ, –≤—Ā–Ķ –Ķ–≥–ĺ –≥–ĺ–ľ–ĺ—ā–ĺ–Ņ–ł—á–Ķ—Ā–ļ–ł–Ķ —Ā–≤–ĺ–Ļ—Ā—ā–≤–į –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć –ĺ–Ņ–ł—Ā–į–Ĺ—č –≤ —ā–Ķ—Ä–ľ–ł–Ĺ–į—Ö –Ķ–≥–ĺ —Ą—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ—Ć–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ—č, –ł–∑–ĺ–ľ–ĺ—Ä—Ą–Ĺ–ĺ–Ļ –≥—Ä—É–Ņ–Ņ–Ķ –ļ–ĺ—Ā. –Ē–į–Ĺ–Ĺ—č–Ļ —Ą–į–ļ—ā —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ļ–ĺ—Ā–≤–Ķ–Ĺ–Ĺ—č–ľ –Ņ–ĺ–ī—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ–ľ –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ–Ļ —Ā–≤—Ź–∑–ł –ľ–Ķ–∂–ī—É –≥—Ä—É–Ņ–Ņ–į–ľ–ł –ļ–ĺ—Ā –ł –≥–ĺ–ľ–ĺ—ā–ĺ–Ņ–ł—á–Ķ—Ā–ļ–ł–ľ–ł –≥—Ä—É–Ņ–Ņ–į–ľ–ł –ī–≤—É–ľ–Ķ—Ä–Ĺ–ĺ–Ļ —Ā—Ą–Ķ—Ä—č[29]. –í–į—Ä–ł–į—Ü–ł–ł –ł –ĺ–Ī–ĺ–Ī—Č–Ķ–Ĺ–ł—Ź–í—č—ą–Ķ–ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ—č–Ķ –ļ–ĺ–Ĺ—Ā—ā—Ä—É–ļ—Ü–ł–ł –ī–ĺ–Ņ—É—Ā–ļ–į—é—ā —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ķ –ĺ–Ī–ĺ–Ī—Č–Ķ–Ĺ–ł–Ķ. –ü—É—Ā—ā—Ć –ł ‚ÄĒ —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ł–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į. –ü—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –ļ–ĺ–Ĺ—Ą–ł–≥—É—Ä–į—Ü–ł–Ļ –≤ ‚ÄĒ —ć—ā–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –≤—Ā–Ķ—Ö —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ł—Ö –≤–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ļ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į –≤ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ . –Ē–į–Ĺ–Ĺ–ĺ–Ķ –Ņ–ĺ–ī–ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–į –≤—Ā–Ķ—Ö –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ—č—Ö –ĺ—ā–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ļ –ł–∑ –≤ —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į–Ķ—ā—Ā—Ź —Ā —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł–Ķ–Ļ, –ł–Ĺ–ī—É—Ü–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ļ —Ā –ļ–ĺ–ľ–Ņ–į–ļ—ā–Ĺ–ĺ-–ĺ—ā–ļ—Ä—č—ā–ĺ–Ļ —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł–ł. –ē—Ā–Ľ–ł —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ļ–ĺ–Ĺ–Ķ—á–Ĺ—č–ľ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ–ľ –ľ–ĺ—Č–Ĺ–ĺ—Ā—ā–ł —Ā –ī–ł—Ā–ļ—Ä–Ķ—ā–Ĺ–ĺ–Ļ —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł–Ķ–Ļ, —ā–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ –≥–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤—É . –ź–Ĺ–į–Ľ–ĺ–≥–ł—á–Ĺ–ĺ –ľ–ĺ–∂–Ĺ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā—Ć –ĺ–Ī–ĺ–Ī—Č–Ķ–Ĺ–ł–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į . –°–ľ. —ā–į–ļ–∂–Ķ
–ü—Ä–ł–ľ–Ķ—á–į–Ĺ–ł—Ź
–õ–ł—ā–Ķ—Ä–į—ā—É—Ä–į
–°—Ā—č–Ľ–ļ–ł
|
Portal di Ensiklopedia Dunia




































































































































![{\displaystyle [0,1]\times [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92f35a051af39d8299688d7c4a63e39ee5f95c8b)


![{\displaystyle x,y\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a89411f493700e4c95ef285820b357955faf5ba7)
![{\displaystyle \{(x,x)|x\in [0,1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b639576993420395759925d3c40e7d5a3c54a736)

![{\displaystyle \{(x,y)\mid x\in [0,1],\,y\in [0,x)\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c541480ba06ddd6a9eaf12a6c555aa7a514a3e3e)

![{\displaystyle x\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64a15936df283add394ab909aa7a5e24e7fb6bb2)
































![{\displaystyle s_{1},s_{2},\ldots ,s_{n}\colon [0,1]\to M}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d52eb9a8298803a50c48cd3ebbe7ef0b894bd912)


![{\displaystyle t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a5c18739ff04858eecc8fec2f53912c348e0e5)





![{\displaystyle [0,1]\times \{1,2,\ldots ,n\}\to \mathbb {R} ^{2}\times [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0349bf3e1729255412ea864b8b4e82e3b911c4b)

























































