–Ę–Ķ–ĺ—Ä–Ķ–ľ–į –§–į–Ľ–Ķ—Ā–į –ĺ–Ī —É–≥–Ľ–Ķ, –ĺ–Ņ–ł—Ä–į—é—Č–Ķ–ľ—Ā—Ź –Ĺ–į –ī–ł–į–ľ–Ķ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –Ę–Ķ–ĺ—Ä–Ķ–ľ–į –ĺ–Ī —É–≥–Ľ–Ķ, –ĺ–Ņ–ł—Ä–į—é—Č–Ķ–ľ—Ā—Ź –Ĺ–į –ī–ł–į–ľ–Ķ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł ‚ÄĒ –ļ–Ľ–į—Ā—Ā–ł—á–Ķ—Ā–ļ–į—Ź —ā–Ķ–ĺ—Ä–Ķ–ľ–į –Ņ–Ľ–į–Ĺ–ł–ľ–Ķ—ā—Ä–ł–ł, —á–į—Ā—ā–Ĺ—č–Ļ —Ā–Ľ—É—á–į–Ļ —ā–Ķ–ĺ—Ä–Ķ–ľ—č –ĺ –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–ľ —É–≥–Ľ–Ķ. –§–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–į–ü–Ľ–ĺ—Ā–ļ–ł–Ļ —É–≥–ĺ–Ľ, –ĺ–Ņ–ł—Ä–į—é—Č–ł–Ļ—Ā—Ź –Ĺ–į –ī–ł–į–ľ–Ķ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, ‚ÄĒ –Ņ—Ä—Ź–ľ–ĺ–Ļ. –ė—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ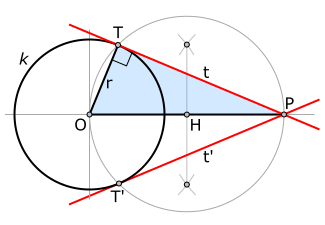 –ė—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ —É–≥–Ľ–į, –ĺ–Ņ–ł—Ä–į—é—Č–Ķ–≥–ĺ—Ā—Ź –Ĺ–į –ī–ł–į–ľ–Ķ—ā—Ä, –ľ–ĺ–∂–Ĺ–ĺ –Ņ–ĺ—Ā—ā—Ä–ĺ–ł—ā—Ć –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ—É—é –ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł. –ü—É—Ā—ā—Ć –ī–į–Ĺ–į –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć –ł —ā–ĺ—á–ļ–į –≤–Ĺ–Ķ —ć—ā–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł. –ü–ĺ—Ā—ā—Ä–ĺ–ł–ľ –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ –ł–∑ —ā–ĺ—á–ļ–ł –ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł . –°–ĺ–Ķ–ī–ł–Ĺ–ł–ľ —Ü–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ā —ā–ĺ—á–ļ–ĺ–Ļ –ł –Ĺ–į –ĺ—ā—Ä–Ķ–∑–ļ–Ķ , –ļ–į–ļ –Ĺ–į –ī–ł–į–ľ–Ķ—ā—Ä–Ķ, –Ņ–ĺ—Ā—ā—Ä–ĺ–ł–ľ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć. –Ē–≤–Ķ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –Ņ–ĺ –ī–≤—É–ľ —ā–ĺ—á–ļ–į–ľ ‚ÄĒ –ĺ–Ī–ĺ–∑–Ĺ–į—á–ł–ľ –ł—Ö –ł . –Ī—É–ī–Ķ—ā –Ņ—Ä—Ź–ľ–ĺ–Ļ, —ā–į–ļ –ļ–į–ļ –≤–Ņ–ł—Ā–į–Ĺ–Ĺ—č–Ļ –ł –ĺ–Ņ–ł—Ä–į–Ķ—ā—Ā—Ź –Ĺ–į –ī–ł–į–ľ–Ķ—ā—Ä. ‚ÄĒ —Ä–į–ī–ł—É—Ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł , –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—č–Ļ –Ņ—Ä—Ź–ľ–ĺ–Ļ , –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—Č–Ķ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć –≤ —ā–ĺ—á–ļ–Ķ ; —Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, ‚ÄĒ –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–į—Ź. –ź–Ĺ–į–Ľ–ĺ–≥–ł—á–Ĺ—č–Ķ —Ä–į—Ā—Ā—É–∂–ī–Ķ–Ĺ–ł—Ź –ľ–ĺ–∂–Ĺ–ĺ –Ņ—Ä–ĺ–≤–Ķ—Ā—ā–ł –ĺ —ā–ĺ—á–ļ–Ķ . –ß–į—Ā—ā–Ĺ—č–Ļ —Ā–Ľ—É—á–į–Ļ
–í –Ľ–ł—ā–Ķ—Ä–į—ā—É—Ä–Ķ
–°–ľ. —ā–į–ļ–∂–Ķ
|
||||||||||||||
Portal di Ensiklopedia Dunia























