Алгебра

А́лгебра (от араб. اَلْجَبْرُ‎^[1] аль-джабр — «восстановление (разрозненных) частей^[2], восстановление равенства, уравнение^[3], восполнение^[4]») — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики; в этом разделе числа и другие математические объекты обозначаются буквами и другими символами, что позволяет записывать и исследовать их свойства в самом общем виде. Слово «алгебра» также употребляется в общей алгебре в названиях различных алгебраических систем. В более широком смысле под «алгеброй» понимают раздел математики, посвящённый изучению операций над элементами множеств произвольной природы, обобщающий обычные операции сложения и умножения чисел^[5].

Алгебра как раздел математики традиционно включает следующие категории.

• Элементарная алгебра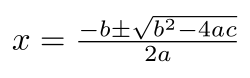, которая изучает свойства операций с вещественными числами. В ней постоянные и переменные обозначаются буквенными символами. Элементарная алгебра содержит правила преобразования алгебраических выражений и уравнений с использованием этих символов. Обычно преподаётся в школе под названием алгебра^[6].
• Общая алгебра, иногда называемая современной алгеброй или абстрактной алгеброй, где аксиоматизируются и изучаются максимально общие алгебраические структуры, такие, как группы, кольца и поля.
• Универсальная алгебра, в которой изучаются свойства, общие для всех алгебраических структур (считается подразделом общей алгебры).
• Линейная алгебра, в которой изучаются свойства векторных пространств (включая матрицы).
• Алгебраическая комбинаторика, в которой методы абстрактной алгебры используются для изучения вопросов комбинаторики.

Элементарная алгебра — раздел алгебры, который изучает самые базовые понятия. Обычно изучается после изучения основных понятий арифметики. В арифметике изучаются числа и простейшие (+, −, ×, ÷) действия с ними. В алгебре числа заменяются на переменные (${\displaystyle a,b,c,x,y}$ и так далее). Такой подход полезен, потому что:

• Позволяет получить общее представление законов арифметики (например, ${\displaystyle a+b=b+a}$ для любых ${\displaystyle a}$ и ${\displaystyle b}$), что является первым шагом к систематическому изучению свойств действительных чисел.
• Позволяет ввести понятие «неизвестного», сформулировать уравнения и изучать способы их решения. (Для примера, «Найти число x, такое что ${\displaystyle 3x+1=10}$» или, в более общем случае, «Найти число x, такое, что ${\displaystyle ax+b=c}$». Это приводит к выводу, что нахождение значения переменной кроется не в природе чисел из уравнения, а в операциях между ними.)
• Позволяет сформулировать понятие функции. (Для примера, «Если вы продали ${\displaystyle x}$ билетов, то ваша прибыль составит ${\displaystyle 3x-10}$ рублей, или ${\displaystyle f(x)=3x-10}$, где ${\displaystyle f}$ — функция, и ${\displaystyle x}$ — число, от которого зависит функция»)

Линейная алгебра — часть алгебры, изучающая векторы, векторные, или линейные пространства, линейные отображения и системы линейных уравнений. К линейной алгебре также относят теорию определителей, теорию матриц, теорию форм (например, квадратичных), теорию инвариантов (частично), тензорное исчисление (частично)^[7]. Современная линейная алгебра делает акцент на изучении векторных пространств^[8].

Линейное, или векторное пространство ${\displaystyle V\left(F\right)}$ над полем ${\displaystyle F}$ — это упорядоченная четвёрка ${\displaystyle (V,F,+,\cdot )}$, где

${\displaystyle V}$ — непустое множество элементов произвольной природы, которые называются векторами;

${\displaystyle F}$ — (алгебраическое) поле, элементы которого называются скалярами;

${\displaystyle +\colon V\times V\to V}$ — операция сложения векторов, сопоставляющая каждой паре элементов ${\displaystyle \mathbf {x} ,\mathbf {y} }$ множества ${\displaystyle V}$ единственный элемент множества ${\displaystyle V}$, обозначаемый ${\displaystyle \mathbf {x} +\mathbf {y} }$;

${\displaystyle \cdot \colon F\times V\to V}$ — операция умножения векторов на скаляры, сопоставляющая каждому элементу ${\displaystyle \lambda }$ поля ${\displaystyle \in F}$ и каждому элементу ${\displaystyle \mathbf {x} }$ множества ${\displaystyle V}$ единственный элемент множества ${\displaystyle V}$, обозначаемый ${\displaystyle \lambda \mathbf {x} }$;

причём заданные операции удовлетворяют следующим аксиомам — аксиомам линейного (векторного) пространства:

1. ${\displaystyle \mathbf {x} +\mathbf {y} =\mathbf {y} +\mathbf {x} }$, для любых ${\displaystyle \mathbf {x} ,\mathbf {y} \in V}$ (коммутативность сложения);
2. ${\displaystyle \mathbf {x} +(\mathbf {y} +\mathbf {z} )=(\mathbf {x} +\mathbf {y} )+\mathbf {z} }$, для любых ${\displaystyle \mathbf {x} ,\mathbf {y} ,\mathbf {z} \in V}$ (ассоциативность сложения);
3. существует такой элемент ${\displaystyle \theta \in V}$, что ${\displaystyle \mathbf {x} +\theta =\mathbf {x} }$ для любого ${\displaystyle \mathbf {x} \in V}$ (существование нейтрального элемента относительно сложения), в частности ${\displaystyle V}$ не пусто;
4. для любого ${\displaystyle \mathbf {x} \in V}$ существует такой элемент ${\displaystyle -\mathbf {x} \in V}$, что ${\displaystyle \mathbf {x} +(-\mathbf {x} )=\theta }$ (существование противоположного элемента относительно сложения).
5. ${\displaystyle \alpha (\beta \mathbf {x} )=(\alpha \beta )\mathbf {x} }$ (ассоциативность умножения на скаляр);
6. ${\displaystyle 1\cdot \mathbf {x} =\mathbf {x} }$ (унитарность: умножение на нейтральный (по умножению) элемент поля F сохраняет вектор).
7. ${\displaystyle (\alpha +\beta )\mathbf {x} =\alpha \mathbf {x} +\beta \mathbf {x} }$ (дистрибутивность умножения на вектор относительно сложения скаляров);
8. ${\displaystyle \alpha (\mathbf {x} +\mathbf {y} )=\alpha \mathbf {x} +\alpha \mathbf {y} }$(дистрибутивность умножения на скаляр относительно сложения векторов).

Евклидовы пространства, аффинные пространства, а также многие другие пространства, изучаемые в геометрии, определяются на основе векторного пространства. Автоморфизмы векторного пространства над полем образуют группу относительно умножения, изоморфную группе невырожденных квадратных матриц, что связывает линейную алгебру с теорией групп, в частности, с теорией линейных представлений групп^[8].

Переход от используемых в линейной алгебре n-мерных векторных пространств к бесконечномерным линейным пространствам нашёл своё отражение в некоторых разделах функционального анализа^[7]. Другим естественным обобщением является использование не поля, а произвольного кольца. Для модуля над произвольным кольцом не выполняются основные теоремы линейной алгебры. Общие свойства векторных пространств над полем и модулей над кольцом изучаются в алгебраической К-теории^[8].

Общая алгебра занимается изучением различных алгебраических систем. В ней рассматриваются свойства операций над объектами независимо от собственно природы объектов^[5]. Она включает в себя в первую очередь теории групп и колец. Общие свойства, характерные для обоих видов алгебраических систем, привели к рассмотрению новых алгебраических систем: решёток, категорий, универсальных алгебр, моделей, полугрупп и квазигрупп. Упорядоченные и топологические алгебры, частично упорядоченные и топологические группы и кольца, также относятся к общей алгебре^[9].

Точная граница общей алгебры не определена. К ней можно также отнести теорию полей, конечных групп, конечномерных алгебр Ли^[9].

Непустое множество ${\displaystyle G}$ с заданной на нём бинарной операцией ${\displaystyle *\,\colon G\times G\to G}$ называется группой ${\displaystyle (G,*)}$, если выполнены следующие аксиомы:

1. ассоциативность: ${\displaystyle \forall (a,b,c\in G):(a*b)*c=a*(b*c)}$;
2. наличие нейтрального элемента: ${\displaystyle \exists e\in G\quad \forall a\in G:(e*a=a*e=a)}$;
3. наличие обратного элемента: ${\displaystyle \forall a\in G\quad \exists a^{-1}\in G:(a*a^{-1}=a^{-1}*a=e)}$

Понятие группы возникло в результате формального описания симметрии и эквивалентности геометрических объектов. В теории Галуа, которая и дала начало понятию группы, группы используются для описания симметрии уравнений, корнями которых являются корни некоторого полиномиального уравнения. Группы повсеместно используются в математике и естественных науках, часто для обнаружения внутренней симметрии объектов (группы автоморфизмов). Почти все структуры общей алгебры — частные случаи групп.

Кольцо — множество R, на котором заданы две бинарные операции: + и × (называемые сложение и умножение), со следующими свойствами:

1. ${\displaystyle \forall a,b\in R\left(a+b=b+a\right)}$ — коммутативность сложения;
2. ${\displaystyle \forall a,b,c\in R\left(a+(b+c))=((a+b)+c\right)}$ — ассоциативность сложения;
3. ${\displaystyle \exists 0\in R\;\forall a\in R\left(a+0=0+a=a\right)}$ — существование нейтрального элемента относительно сложения;
4. ${\displaystyle \forall a\in R\;\exists b\in R\left(a+b=b+a=0\right)}$ — существование противоположного элемента относительно сложения;
5. ${\displaystyle \forall a,b,c\in R\;(a\times b)\times c=a\times (b\times c)}$ — ассоциативность умножения (некоторые авторы не требуют выполнения этой аксиомы^[10])
6. ${\displaystyle \forall a,b,c\in R\left\{{\begin{matrix}a\times (b+c)=a\times b+a\times c\\(b+c)\times a=b\times a+c\times a\end{matrix}}\right.}$ — дистрибутивность.

Универсальная алгебра является специальным разделом общей алгебры, который занимается изучением характерных для всех алгебраических систем свойств. Алгебраическая система представляет собой произвольное непустое множество с заданным (возможно, бесконечным) набором конечноарных операций над ним и конечноарных отношений: ${\displaystyle {\mathfrak {A}}=\langle A,F,R\rangle }$, ${\displaystyle F=\langle f_{1}:A^{n_{1}}\to A,\dots f_{i}:A^{n_{i}}\to A,\dots \rangle }$, ${\displaystyle R=\langle r_{1}\subseteq A^{m_{1}},\dots r_{i}\subseteq A^{m_{i}},\dots \rangle }$. Множество ${\displaystyle A}$ в этом случае называется носителем (или основным множеством) системы, набор функциональных и предикатных символов с их арностями ${\displaystyle \langle F,R,\langle n_{1},\dots n_{i},\dots \rangle ,\langle m_{1}\dots m_{i},\dots \rangle \rangle }$ — её сигнатурой. Система с пустым множеством отношений называется универсальной алгеброй (в контексте предмета — чаще просто алгеброй), а с пустым множеством операций — моделью или системой отношений, реляционной системой.

В терминах универсальной алгебры, например, кольцо — это универсальная алгебра ${\displaystyle \left(R,+,\times \right)}$, такая, что алгебра ${\displaystyle \left(R,+\right)}$ — абелева группа, и операция ${\displaystyle +}$ дистрибутивна слева и справа относительно ${\displaystyle \times }$. Кольцо называется ассоциативным, если мультипликативный группоид является полугруппой.

Раздел рассматривает как собственно универсальные алгебры, так и сопутствующие структуры: моноид всех эндоморфизмов ${\displaystyle \mathbf {End} {\mathfrak {A}}}$, группа всех автоморфизмов ${\displaystyle \mathbf {Aut} {\mathfrak {A}}}$, решётки всех подалгебр ${\displaystyle \mathbf {Sub} {\mathfrak {A}}}$ и всех конгруэнций ${\displaystyle \mathbf {Con} {\mathfrak {A}}}$^[11].

Универсальная алгебра находится на стыке логики и алгебры^[9].

Истоки алгебры уходят к временам глубокой древности. Арифметические действия над натуральными числами и дробями — простейшие алгебраические операции — встречаются в ранних математических текстах^[6]. Ещё в 1650 году до н. э. египетские писцы могли решать отвлечённые уравнения первой степени и простейшие уравнения второй степени, к ним относятся задачи 26 и 33 из папируса Ринда и задача 6 из Московского папируса (так называемые задачи на «аха»). Предполагается, что решение задач было основано на правиле ложного положения^[12]. Это же правило, правда, крайне редко, использовали вавилоняне^[13].

Вавилонские математики умели решать квадратные уравнения. Они имели дело только с положительными коэффициентами и корнями уравнения, так как не знали отрицательных чисел. По разным реконструкциям в Вавилоне знали либо правило для квадрата суммы, либо правило для произведения суммы и разности, вместе с тем метод вычисления корня полностью соответствует современной формуле. Встречаются и уравнения третьей степени^[14]. Кроме того, в Вавилоне была введена особая терминология, использовались шумерские клинописные знаки для обозначения первого неизвестного («длины»), второго неизвестного («ширины»), третьего неизвестного («глубины»), а также различных производных величин («поля» как произведения «длины» и «ширины», «объёма» как произведения «длины», «ширины» и «глубины»), которые можно считать математическими символами, так как в обычной речи уже использовался аккадский язык. Несмотря на явное геометрическое происхождение задач и терминов, использовались они отвлечённо, в частности, «площадь» и «длина» считались однородными^[13]. Для решения квадратных уравнений было необходимо уметь осуществлять различные тождественные алгебраические преобразования, оперировать неизвестными величинами. Таким образом был выделен целый класс задач, для решения которых необходимо пользоваться алгебраическими приёмами^[14].

За 2000 лет до нашего времени китайские учёные решали уравнения первой степени и их системы, а также квадратные уравнения (см. Математика в девяти книгах). Они уже знали отрицательные и иррациональные числа. Поскольку в китайском языке каждый символ обозначает понятие, то сокращений не было. Наряду с индийскими и исламскими математиками, китайские математики открыли «треугольник Паскаля» задолго до европейцев^[15].

После того как была открыта несоизмеримость стороны и диагонали квадрата, греческая математика переживала кризис, разрешению которого способствовал выбор геометрии как основы математики и определение алгебраических операций для геометрических величин. Геометрической алгебре посвящена вторая книга «Начал» Евклида, работы Архимеда и Аполлония. С использованием отрезков, прямоугольников и параллелепипедов были определены сложение и вычитание, произведение (построенный на двух отрезках прямоугольник). Такое представление позволило доказать дистрибутивный закон умножения относительно сложения, тождество для квадрата суммы. Алгебра первоначально была основана на планиметрии и приспособлена в первую очередь для решения квадратных уравнений^[16]. Вместе с тем к алгебраическим уравнениям сводятся сформулированные пифагорейцами задачи об удвоении куба и трисекции угла, построение правильных многоугольников^[17]. Решение кубических уравнений получило своё развитие в работах Архимеда (сочинения «О шаре и цилиндре» и «О коноидах и сфероидах»), который исследовал в общем виде уравнение ${\displaystyle x^{3}+ax+b=0}$. Отдельные задачи решались с помощью конических сечений^[18].

Неожиданный переход к алгебре, основанной на арифметике, произошёл в работах Диофанта, который ввёл буквенные обозначения: неизвестное число он назвал «число», вторую степень неизвестного — «квадрат», третью — «куб», четвёртую — «квадрато-квадрат», пятую — «квадрато-куб», шестую — «кубо-куб». Также он ввёл обозначения для отрицательных степеней, свободного члена, отрицательного числа (или вычитания) и знака равенства. Диофант знал и использовал правило переноса вычитаемого из одной части уравнения в другую и правило сокращения равных членов^[19]. Исследуя уравнения третьей и четвёртой степеней, Диофант для нахождения рациональной точки на кривой использует такие методы геометрической алгебры, как провести касательную в рациональной точке кривой или провести прямую через две рациональные точки. В X веке «Арифметика» Диофанта, в которой он изложил свои методы, была переведена на арабский язык, а в XVI веке достигла Западной Европы, оказав влияние на работы Ферма и Виета. Идеи Диофанта можно заметить также в работах Эйлера, Якоби, Пуанкаре и других математиков вплоть до начала XX века. В настоящее время проблемы Диофанта принято относить к алгебраической геометрии^[20].

Термин «алгебра» взят из сочинения среднеазиатского учёного аль-Хорезми «Китаб аль-джебр ва-ль-мукабала» (ок. 825 года). Слово «аль-джабр» при этом означало операцию переноса вычитаемых из одной части уравнения в другую с противоположным знаком, и его буквальный смысл — «восполнение», «взвешивание»^[4]. Арабские математики рассматривали члены уравнений как массы гирь на весах, которые надо было перенести на другую чашу весов, чтобы уравновесить весы (перенос членов из правой части уравнения в левую с противоположным знаком и наоборот); или как одинаковые гири на обеих чашах, которые можно было убрать с обоих чаш без нарушения равновесия (сокращение членов уравнения). «Аль-мукабала» означало отбрасывание в обеих частях равенства равных членов (противоположение). «Аль-джабр» при переводе на латинский язык превратилось в «algebra», а аль-мукабала была отброшена: так появилось название «алгебра». Аль-Хорезми разработал системный подход к решению линейных и квадратных уравнений, заложив основу этой математической дисциплины.

В X–XI веках алгебру расширили Абу Камил и аль-Караджи, введя иррациональные числа, систематизировав операции с многочленами и заложив основы математической индукции. XII век ознаменовался работами Омара Хайяма, который развил геометрическое решение кубических уравнений и дал первое определение алгебры как науки. Аль-Самуал ввёл правила умножения одночленов любых целых степеней и правила деления многочленов, а Шараф ад-Дин Ат-Туси использовал понятия функции и дискриминанта кубического уравнения. Постепенно алгебра перешла от словесных описаний к символическому выражению, что стало важным шагом в её развитии.

Перевод труда аль-Хорезми на латинский язык способствовал распространению алгебры в Европе и её дальнейшему совершенствованию. В XVI веке в Европе были открыты способы решения уравнений 3 и 4 степеней. Распространение получили отрицательные и комплексные числа. В XIX веке было доказано, что любое уравнение 5 степени и выше нельзя решить алгебраическим способом. Вплоть до второй половины XX века практическое применение алгебры ограничивалось, в основном, решением алгебраических уравнений и систем уравнений с несколькими переменными.

Во второй половине XX века началось бурное развитие ряда новых отраслей техники. Появились электронно-вычислительные машины, устройства для хранения, переработки и передачи информации, системы наблюдения типа радара. Проектирование новых видов техники и их использование немыслимо без применения современной алгебры. Так, электронно-вычислительные машины устроены по принципу конечных автоматов. Для проектирования электронно-вычислительных машин и электронных схем используются методы булевой алгебры. Современные языки программирования для ЭВМ основаны на принципах теории алгоритмов. Теория множеств используется в системах компьютерного поиска и хранения информации. Теория категорий используется в задачах распознавания образов, определении семантики языков программирования, и других практических задачах. Кодирование и декодирование информации производится методами теории групп. Теория рекуррентных последовательностей используется в работе радаров. Экономические расчёты невозможны без использования теории графов. Математическое моделирование широко использует все разделы алгебры.

Титул «отца алгебры» часто приписывают аль-Хорезми^[21][22][23]. Среди прочих, эту точку зрения поддерживают такие историки математики, как Соломон Гандз^[24], Карл Бенджамин Бойер^[25] и Бартель Леендерт ван дер Варден^[26]. Впрочем, иногда данное звание приписывают и Диофанту. Его сторонники указывают, что уравнения, изложенные в «Арифметике», используют некоторые символьные обозначения, тогда как в «Китаб аль-джебр ва-ль-мукабала» уравнения и их решения передаются исключительно словами^[27]. Однако историк математики Курт Фогель^[англ.] однозначно выступает против того, чтобы Диофант носил этот титул^[28], поскольку его арифметика была не намного более алгебраической, чем математика древних вавилонян^[29].

Сторонники аль-Хорезми указывают на тот факт, что он дал исчерпывающее и систематическое объяснение алгебраического решения квадратных уравнений с положительными корнями^[30]. Он был первым, кто преподавал алгебру в элементарной форме ради самой этой дисциплины, в то время как Диофант в первую очередь занимался теорией чисел^[24]. Другие его сторонники добавляют, что в отличие от вавилонских табличек и от «Арифметики» Диофанта его алгебра больше не была связана с рядом задач, которые нужно решить, но с изложением, которое начинается с примитивных терминов, комбинации которых должны дать все возможные виды уравнений, отныне явно становящихся истинным объектом исследования^[31]. Виктор Джозеф Кац^[англ.] также считает «Китаб аль-джебр ва-ль-мукабала» первым настоящим текстом по алгебре, сохранившимся до наших дней^[32].

• Gandz, Solomon (1936), The sources of al-Khwarizmi's algebra, Osiris
• История математики: в 3 т / под редакцией А. П. Юшкевича. — М.: Наука, 1970. — Т. I: С древнейших времён до начала Нового времени.
• Никифоровский В. А. Из истории алгебры XVI-XVII вв. — М.: Наука, 1979. — С. 174—204. — 208 с. — (История науки и техники).
• Boyer, Carl B. (1991), A History of Mathematics (2nd ed.), John Wiley & Sons, Inc., ISBN 978-0-471-54397-8
• Derbyshire, John (2006), Unknown Quantity: A Real And Imaginary History of Algebra, Washington, DC: Joseph Henry Press, ISBN 978-0-309-09657-7

	В Викисловаре есть статья «алгебра»

• Алгебра в каталоге ссылок Curlie (dmoz)
• Информация на начало XX века: Алгебра // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.