Хәрәкәтсез хисап системасына (зәңгәр сәгатенә) карата хәрәкәт итүче (әйләнүче) хисап системасында (кызыл сәгате) вакыт әкренрәк бара Вакытның релятивистик әкренәүе - Махсус чагыштырмалылык теориясендә кинематик эффект буенча хәрәкәтләнә торган җисемдә хәрәкәтсез хисап системасына карата барлык физик күренешләр әкренрәк баралар.
Иярчендә урнашкан сәгатьләр бер көндә җирдәгенекедән 38 микросекундада әкренрәк бара Вакытның релятивистик әкренәүенә күрә Җирнең атмосферасы югары катламнарында хасил булган кыска вакыт яшәүче элементар кисәкчекләр Җирнең өслегенә җитәләр.
Әлеге күренеш вакытның гравитацион әкренәюе белән иярчен навигация системаларында (мәсәлән GPS ) исәпкә алына: иярчендә урнашкан сәгатьләр бер көндә 38 микросекундада әкренрәк бара.
Вакытның релятивистик әкренәүенең мөһим мисалы - игезәкләр парадоксы .
Лоренц рәвешүзгәртүләреннән вакытның релятивистик әкренәүе чыгарыла:
Δ
t
=
Δ
t
0
1
−
v
2
/
c
2
{\displaystyle \Delta t={\frac {\Delta t_{0}}{\sqrt {1-v^{2}/c^{2}}}}}
биредә:
Δ
t
{\displaystyle \Delta t}
Δ
t
0
{\displaystyle \Delta t_{0}}
v
{\displaystyle v}
c
{\displaystyle c}
вакуумда яктылык тизлеге .Тигезләмәнең төгәллеге күп тапкыр уңай тикшерелгән.
Шулай ук озынлыкның релятивистик кыскаруы чыгарыла.
Вакытның релятивистик әкренәюе һәм озынлыкның релятивистик кыскаруының төп сәбәбе - баштарак пастулатланган, ә соңрак исбатланган төрле хисап системаларында вакуумда яктылык тизлегенең үзгәрмәүчәнлеге (даимилеге).
Нәкъ әлеге мәсләктән вакытның релятивистик әкренәюе чыгарыла. Яктылык сәгате схемасы ярдәмендә әлеге эффект күзәтелә:
Яктылык сәгате хисап системасында көзгедән көзгегә хәрәкәт вакыты:
Δ
t
0
=
L
/
c
{\displaystyle \textstyle \Delta t_{0}=L/c}
Әгәр яктылык сәгәте
v
{\displaystyle \textstyle v}
хәрәкәтсез күзәтүчегә карата яктылык гипотенуза буйлап бара, Пифагор теоремасы буенча:
(
c
Δ
t
)
2
=
(
c
Δ
t
0
)
2
+
(
v
Δ
t
)
2
.
{\displaystyle (c\,\Delta t)^{2}=(c\,\Delta t_{0})^{2}+(v\,\Delta t)^{2}.}
Шуннан Вакытның релятивистик әкренәюе чыгарыла.
Яки:
Δ
t
=
2
L
c
.
{\displaystyle \Delta t={\frac {2L}{c}}.}
Δ
t
′
=
2
D
c
.
{\displaystyle \Delta t'={\frac {2D}{c}}.}
D
=
(
1
2
v
Δ
t
′
)
2
+
L
2
.
{\displaystyle D={\sqrt {\left({\frac {1}{2}}v\Delta t'\right)^{2}+L^{2}}}.}
Δ
t
′
=
1
c
(
v
Δ
t
′
)
2
+
(
2
L
)
2
(
Δ
t
′
)
2
=
v
2
c
2
(
Δ
t
′
)
2
+
(
2
L
c
)
2
(
1
−
v
2
c
2
)
(
Δ
t
′
)
2
=
(
2
L
c
)
2
(
Δ
t
′
)
2
=
(
2
L
c
)
2
1
−
v
2
c
2
Δ
t
′
=
2
L
c
1
−
v
2
c
2
{\displaystyle {\begin{aligned}\Delta t'&={\frac {1}{c}}{\sqrt {\left(v\Delta t'\right)^{2}+\left(2L\right)^{2}}}\\\left(\Delta t'\right)^{2}&={\frac {v^{2}}{c^{2}}}(\Delta t')^{2}+\left({\frac {2L}{c}}\right)^{2}\\\left(1-{\frac {v^{2}}{c^{2}}}\right)\left(\Delta t'\right)^{2}&=\left({\frac {2L}{c}}\right)^{2}\\\left(\Delta t'\right)^{2}&={\frac {\left({\frac {2L}{c}}\right)^{2}}{1-{\frac {v^{2}}{c^{2}}}}}\\[3pt]\Delta t'&={\frac {\frac {2L}{c}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}\\\end{aligned}}}
Δ
t
′
=
Δ
t
1
−
v
2
c
2
{\displaystyle \Delta t'={\frac {\Delta t}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}
Алмаш тизлекле җисем өчен вакытның әкренәюе интеграл ярдәмендә исәпләнә:
Δ
t
0
=
∫
t
1
t
2
1
−
v
2
(
τ
)
/
c
2
d
τ
.
{\displaystyle \Delta t_{0}=\int \limits _{t_{1}}^{t_{2}}{\sqrt {1-\mathbf {v} ^{2}(\tau )/c^{2}}}\,d\tau .}
Интеграл юл буйлап алына.
Δ
t
0
{\displaystyle \textstyle \Delta t_{0}}
үз вакыты дип йөртелә.
Вакытның әкренәюе тик тизлек белән билгеләнә, тизләнеш йогынты ясамый.
CERN Storage-Ring тизләткечендә мюоннар тизлеге
v
=
0,999
4
c
{\displaystyle \textstyle v=0{,}9994\,c}
1
/
1
−
(
v
/
c
)
2
≈
29
{\displaystyle \textstyle 1/{\sqrt {1-(v/c)^{2}}}\approx 29}
a
∼
10
18
⋅
g
{\displaystyle \textstyle a\sim 10^{18}\cdot g}
g
=
9
,
8
{\displaystyle \textstyle g=9{,}8}
ирекле төшү тизләнеше )
Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 8-е, стереотипное. — М.: Физматлит, 2006. — 534 с. — («Теоретическая физика», том II). — ISBN 5-9221-0056-4
Bailey J. et al. — Measurements of relativistic time dilatation for positive and negative muons in circular orbit, Nature, v.268, p. 301-305 (1977)
Я.П. Терлецкий. Парадоксы Теории Относительности. — М.: Наука, 1966. — С. 40 – 42.
Х.Х. Ыйглайне. В мире больших скоростей. — M.: Наука, 1966. — С. 100-105. 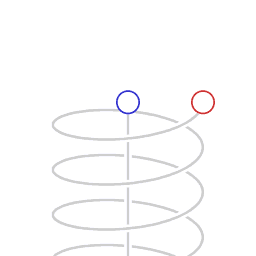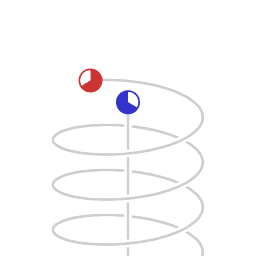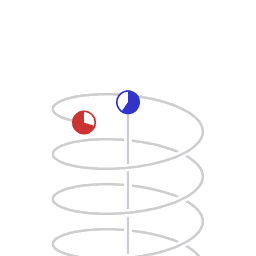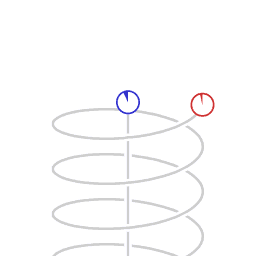













![{\displaystyle {\begin{aligned}\Delta t'&={\frac {1}{c}}{\sqrt {\left(v\Delta t'\right)^{2}+\left(2L\right)^{2}}}\\\left(\Delta t'\right)^{2}&={\frac {v^{2}}{c^{2}}}(\Delta t')^{2}+\left({\frac {2L}{c}}\right)^{2}\\\left(1-{\frac {v^{2}}{c^{2}}}\right)\left(\Delta t'\right)^{2}&=\left({\frac {2L}{c}}\right)^{2}\\\left(\Delta t'\right)^{2}&={\frac {\left({\frac {2L}{c}}\right)^{2}}{1-{\frac {v^{2}}{c^{2}}}}}\\[3pt]\Delta t'&={\frac {\frac {2L}{c}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a029598f84178773b6a9a9e855dd6096e30374ff)




















