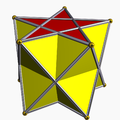
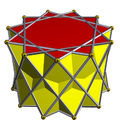
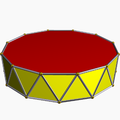
Призматичний однорідний многогранник Призмати́чний однорі́дний многогранник — однорідний многогранник з діедричною симетрією[en]. Вони утворюють два нескінченних сімейства: однорідні призми та однорідні антипризми. Всі вони мають вершини на двох паралельних площинах, а тому всі є призматоїдами. Вершинна конфігурація та групи симетріїОскільки вони є ізогональними (вершинно-транзитивними), їхнє розташування вершин[en] однозначно відповідає групам симетрії . Різниця між призматичними та антипризматичними групами симетрії полягає в тому, що Dph має ребра, які зв'язують вершини на двох площинах, перпендикулярні цим площинам, що задає площину симетрії, паралельну многокутникам, тоді як Dpd має ребра, що схрещуються, що дає обертову симетрію. Кожне тіло має p площин відбитків, які містять p-кратні осі многокутників. Група симетрії Dph містить центральну симетрію тоді й лише тоді, коли p парне, тоді як Dpd містить центральну симетрію тоді й лише тоді, коли p непарне. СписокІснують:
Якщо p/q є цілим числом, тобто. q = 1, призма або антипризма опукла. (Дріб завжди вважається нескоротним.) Антипризма з p/q < 2 є самоперетинною або виродженою, її вершинна фігура схожа на краватку-метелика. З p/q ≤ 3/2 однорідних антипризм не існує, оскільки їхня вершинна фігура порушила б нерівність трикутника. МалюнкиЗауваження: тетраедр, куб і октаедр перераховані нижче як такі, що мають діедричну симетрію (як діагональна антипризма, квадратна призма і трикутна антипризма відповідно), хоча, при однорідному розфарбовуванні, тетраедр також має симетрію тетраедричну, а куб і октаедр мають октаедричну.
Див. такожПриміткиЛітература
Посилання |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia