Соленоїдне векторне поле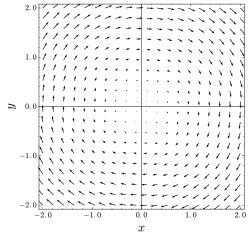

У векторному численні соленоїдне векторне поле (також відоме як нести́сливе векторне поле або бездивергентне векторне поле ) — це векторне поле v з нульовою дивергенцією в усіх точках поля:

${\displaystyle \nabla \cdot \mathbf {v} =0.\,}$

Фундаментальна теорема векторного числення стверджує, що будь-яке векторне поле можна виразити як суму безвихорового і соленоїдного полів. Умова нульової дивергенції задовольняється, коли векторне поле v має векторний потенціал, оскільки визначення векторного потенціалу A як:

${\displaystyle \mathbf {v} =\nabla \times \mathbf {A} }$

автоматично дає тотожність:

${\displaystyle \nabla \cdot \mathbf {v} =\nabla \cdot (\nabla \times \mathbf {A} )=0.}$

Обернене твердження також правильне: для будь-якого соленоїдного поля v існує векторний потенціал A такий, що ${\displaystyle \mathbf {v} =\nabla \times \mathbf {A} .}$ (Строго кажучи, це виконується лише за деяких технічних умов на v, див. теорема розкладання Гельмгольца.)

Формула Остроградського дає тотожне інтегральне визначення соленоїдного поля; а саме, що для всякої замкненої поверхні, загальний потік крізь поверхню має дорівнювати нулю:

${\displaystyle \;\;\mathbf {v} \cdot \,d\mathbf {S} =0,}$

де ${\displaystyle d\mathbf {S} =\mathbf {n} \cdot S}$, а ${\displaystyle \mathbf {n} }$ — зовнішня нормаль для кожного елемента поверхні.

Соленоїдний походить від грецького слова соленоїд (σωληνοειδές - sōlēnoeidēs), що означає трубоподібний.

• магнітне поле B є соленоїдним (див. Рівняння Максвелла);
• поле швидкості нести́сливої рідини є соленоїдним (випливає з ${\displaystyle {\frac {\partial \rho }{\partial t}}=0}$);
• Електричне поле в областях, де відсутні джерела (заряди). Для соленоїдності поля E необхідна умова (або взаємна компенсація) вільних і зв'язаних зарядів.
• Поле вектора густини струму соленоїдальне за умови відсутності зміни густини заряду із часом (тоді соленоїдальність струму випливає з рівняння неперервності).

• Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2025. — 2391 с.(укр.)

• Weisstein, Eric W. Соленоїдне векторне поле(англ.) на сайті Wolfram MathWorld.