Термодинамічна бета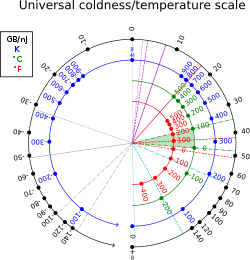

У статистичній термодинаміці термодинамічна бета, також відома як холодність,^[1] є величиною, оберненою до термодинамічної температури системи:$${\displaystyle \beta ={\frac {1}{k_{\rm {B}}T}}}$$ (де T — температура, а k_B — стала Больцмана).^[2]

Термодинамічна бета має розмірність, обернену до енергії (в одиницях СІ, обернений джоуль, ${\displaystyle [\beta ]={\textrm {J}}^{-1}}$). У нетеплових одиницях її також можна вимірювати в байтах на джоуль або, що зручніше, в гігабайтах на наноджоуль;^[3] 1 K⁻¹ еквівалентний приблизно 13 062 гігабайтам на наноджоуль; при кімнатній температурі: T = 300 K, β ≈ 44 ГБ/нДж ≈ 39 еВ⁻¹ ≈ 2.4×10²⁰ Дж⁻¹. Коефіцієнт перетворення: 1 ГБ/нДж = ${\displaystyle 8\ln 2\times 10^{18}}$ Дж⁻¹.

Термодинамічна бета, по суті, є сполучною ланкою між теорією інформації та статистичною механікою в інтерпретації фізичної системи через її ентропію і термодинамікою, пов'язаною з її енергією. Вона виражає реакцію ентропії на збільшення енергії. Якщо до системи додається невелика кількість енергії, то β описує ступінь рандомізації системи.

Через статистичне визначення температури як функції ентропії, функцію холодності можна обчислити в мікроканонічному ансамблі за формулою

${\displaystyle \beta ={\frac {1}{k_{\rm {B}}T}}\,={\frac {1}{k_{\rm {B}}}}\left({\frac {\partial S}{\partial E}}\right)_{V,N}}$

(тобто часткова похідна ентропії S за енергією E при постійному об'ємі V і числі частинок N).

Хоча β повністю еквівалентна температурі за концептуальним змістом, вона зазвичай вважається більш фундаментальною величиною, ніж температура, через явище від'ємної температури, при якій β неперервна при переході через нуль, тоді як T має сингулярність.^[4]

Крім того, у β є перевага в тому, що її причинно-наслідковий зв'язок легше зрозуміти: якщо до системи додається невелика кількість тепла, β представляє збільшення ентропії, поділене на збільшення тепла. Температуру складно інтерпретувати в тому ж сенсі, оскільки неможливо "додати ентропію" до системи інакше, як опосередковано, змінюючи інші величини, такі як температура, об'єм або число частинок.

З точки зору статистики, β — це числова величина, що пов'язує дві макроскопічні системи в рівновазі. Точне формулювання наступне. Розглянемо дві системи, 1 і 2, що перебувають у тепловому контакті, з відповідними енергіями E₁ і E₂. Припустимо, що E₁ + E₂ = деяка постійна E. Кількість мікростанів кожної системи позначимо Ω₁ і Ω₂. У рамках наших припущень Ω_i залежить тільки від E_i. Ми також припускаємо, що будь-який мікростан системи 1, сумісний з E₁, може співіснувати з будь-яким мікростаном системи 2, сумісним з E₂. Таким чином, кількість мікростанів для об'єднаної системи дорівнює

${\displaystyle \Omega =\Omega _{1}(E_{1})\Omega _{2}(E_{2})=\Omega _{1}(E_{1})\Omega _{2}(E-E_{1}).\,}$

Ми виведемо β з основного постулату статистичної механіки:

Коли об'єднана система досягає рівноваги, число Ω максимізується.

(Іншими словами, система природним чином прагне до максимального числа мікростанів.) Отже, в рівновазі:

${\displaystyle {\frac {d}{dE_{1}}}\Omega =\Omega _{2}(E_{2}){\frac {d}{dE_{1}}}\Omega _{1}(E_{1})+\Omega _{1}(E_{1}){\frac {d}{dE_{2}}}\Omega _{2}(E_{2})\cdot {\frac {dE_{2}}{dE_{1}}}=0.}$

Але E₁ + E₂ = E має на увазі

${\displaystyle {\frac {dE_{2}}{dE_{1}}}=-1.}$

Отже

${\displaystyle \Omega _{2}(E_{2}){\frac {d}{dE_{1}}}\Omega _{1}(E_{1})-\Omega _{1}(E_{1}){\frac {d}{dE_{2}}}\Omega _{2}(E_{2})=0}$

тобто

${\displaystyle {\frac {d}{dE_{1}}}\ln \Omega _{1}={\frac {d}{dE_{2}}}\ln \Omega _{2}\quad {\mbox{в рівновазі.}}}$

Вищенаведене співвідношення мотивує визначення β:

${\displaystyle \beta ={\frac {d\ln \Omega }{dE}}.}$

Коли дві системи перебувають у рівновазі, вони мають однакову термодинамічну температуру T. Тому інтуїтивно можна очікувати, що β (визначена через мікростани) якимось чином пов'язана з T. Цей зв'язок забезпечується основним постулатом Больцмана, записаним як

${\displaystyle S=k_{\rm {B}}\ln \Omega ,}$

де k_B — стала Больцмана, S — класична термодинамічна ентропія, а Ω — число мікростанів. Таким чином,

${\displaystyle d\ln \Omega ={\frac {1}{k_{\rm {B}}}}dS.}$

Підставляючи у визначення β зі статистичного визначення вище, отримуємо

${\displaystyle \beta ={\frac {1}{k_{\rm {B}}}}{\frac {dS}{dE}}.}$

Порівнюючи з термодинамічною формулою

${\displaystyle {\frac {dS}{dE}}={\frac {1}{T}},}$

маємо

${\displaystyle \beta ={\frac {1}{k_{\rm {B}}T}}={\frac {1}{\tau }}}$

де ${\displaystyle \tau }$ називається фундаментальною температурою системи і має розмірність енергії.

Термодинамічна бета була спочатку введена в 1971 році (як Kältefunktion «функція холодності») Інго Мюллером, одним із прихильників школи думки раціональної термодинаміки,^[5][6] на основі більш ранніх пропозицій про функцію «оберненої температури».^{[1][7][первинне джерело]}

Розподіл Больцмана

Канонічний ансамбль

Модель Ізинга