еә§жЁҷйҷҚдёӢжі• пјҲгҒ–гҒІгӮҮгҒҶгҒ“гҒҶгҒӢгҒ»гҒҶгҖҒиӢұ : Coordinate descent пјүгҒЁгҒҜгҖҒй–ўж•° гҒ®жҘөеҖӨгӮ’йҖҗж¬Ўеә§жЁҷж–№еҗ‘гҒ«жңҖе°ҸеҢ–гҒ—гҒҰжұӮгӮҒгӮӢжңҖйҒ©еҢ–гӮўгғ«гӮҙгғӘгӮәгғ гҒ®дёҖзЁ®гҖӮеҗ„еҸҚеҫ©гҒ«гҒҠгҒ„гҒҰеә§жЁҷйҷҚдёӢжі•гҒҜеә§жЁҷйҒёжҠһиҰҸеүҮгҒ«еҫ“гҒЈгҒҰеә§жЁҷ гҒӮгӮӢгҒ„гҒҜеә§жЁҷгғ–гғӯгғғгӮҜгӮ’жұәе®ҡгҒ—гҖҒйҒёжҠһгҒ•гӮҢгҒҰгҒ„гҒӘгҒ„еә§жЁҷгӮ„еә§жЁҷгғ–гғӯгғғгӮҜгӮ’еӣәе®ҡгҒ—гҒҹгҒҫгҒҫгҒқгҒ®еә§жЁҷи¶…е№ійқўдёҠгҒ§еҺіеҜҶгҒӮгӮӢгҒ„гҒҜиҝ‘дјјзҡ„гҒ«жңҖе°ҸеҢ–гҒҷгӮӢгҖӮеә§жЁҷж–№еҗ‘гҒ«зӣҙз·ҡжҺўзҙў гӮ’иЎҢгҒҶгҒ“гҒЁгҒ§зҸҫеңЁгҒ®еҸҚеҫ©зӮ№гҒ«гҒҠгҒ‘гӮӢйҒ©еҲҮгҒӘгӮ№гғҶгғғгғ—гӮөгӮӨгӮәгӮ’жұӮгӮҒгӮӢгҒ“гҒЁгҒҢгҒ§гҒҚгӮӢгҖӮеә§жЁҷйҷҚдёӢжі•гҒҜеҫ®еҲҶеҸҜиғҪгғ»еҫ®еҲҶдёҚеҸҜиғҪгҒӘй–ўж•°дёЎиҖ…гҒЁгӮӮгҒ«йҒ©з”ЁгҒ§гҒҚгӮӢи§Јжі•гҒ§гҒӮгӮӢгҖӮ
еә§жЁҷйҷҚдёӢжі•гҒҜеҗ„еҸҚеҫ©гҒ«гҒҠгҒ„гҒҰдёҖгҒӨгҒ®пјҲгҒӮгӮӢгҒ„гҒҜе°‘ж•°гҒ®пјүеӨүж•°гҒ®жңҖйҒ©еҢ–е•ҸйЎҢгӮ’и§ЈгҒҸгӮҲгҒҶгҒ«гҖҒеӨүж•°гҒ®еҗ„ж–№еҗ‘гҒ«й Ҷз•ӘгҒ«жңҖе°ҸеҢ–гҒҷгӮӢгҒ“гҒЁгҒ§еӨҡеӨүж•°й–ўж•°
F
(
x
)
{\displaystyle F(\mathbf {x} )}
[ 1]
x
0
=
(
x
1
0
,
вҖҰ
,
x
n
0
)
{\displaystyle \mathbf {x} ^{0}=(x_{1}^{0},\ldots ,x_{n}^{0})}
k
+
1
{\displaystyle k+1}
x
k
+
1
{\displaystyle \mathbf {x} ^{k+1}}
x
k
{\displaystyle \mathbf {x} ^{k}}
x
i
k
+
1
=
a
r
g
m
i
n
y
вҲҲ
R
f
(
x
1
k
+
1
,
вҖҰ
,
x
i
вҲ’
1
k
+
1
,
y
,
x
i
+
1
k
,
вҖҰ
,
x
n
k
)
{\displaystyle x_{i}^{k+1}={\underset {y\in \mathbb {R} }{\operatorname {arg\,min} }}\;f(x_{1}^{k+1},\dots ,x_{i-1}^{k+1},y,x_{i+1}^{k},\dots ,x_{n}^{k})}
[ 2] гҒҹгҒ гҒ—гҖҒеӨүж•°
x
i
{\displaystyle x_{i}}
x
{\displaystyle \mathbf {x} }
n
{\displaystyle n}
i
{\displaystyle i}
гҒҷгҒӘгӮҸгҒЎгҖҒй–ўж•°
F
{\displaystyle F}
x
0
{\displaystyle \mathbf {x} ^{0}}
x
0
,
x
1
,
x
2
,
вҖҰ
{\displaystyle \mathbf {x} ^{0},\mathbf {x} ^{1},\mathbf {x} ^{2},\dots }
еҗ„еҸҚеҫ©гҒ«гҒҠгҒ„гҒҰзӣҙз·ҡжҺўзҙў гӮ’иЎҢгҒҶгҒ“гҒЁгҒ§д»ҘдёӢгҒ®жҖ§иіӘгҒҢе°ҺгҒӢгӮҢгӮӢ:
F
(
x
0
)
вүҘ
F
(
x
1
)
вүҘ
F
(
x
2
)
вүҘ
вҖҰ
.
{\displaystyle F(\mathbf {x} ^{0})\geq F(\mathbf {x} ^{1})\geq F(\mathbf {x} ^{2})\geq \dots .}
гҒ“гҒ®зӮ№еҲ—гҒҜжңҖжҖҘйҷҚдёӢжі•гҒЁеҗҢж§ҳгҒ«жҘөеҖӨгҒёгҒ®еҸҺжқҹжҖ§гӮ’жҢҒгҒӨгҒ“гҒЁгҒҢзҹҘгӮүгӮҢгҒҰгҒ„гӮӢгҖӮзӣҙз·ҡжҺўзҙў гҒ«гӮҲгӮӢеә§жЁҷж–№еҗ‘гҒёгҒ®жҺўзҙўгҒҢдёҖйҖҡгӮҠе·ЎеӣһгҒ—гҒҹеҫҢгҒ§гӮӮзӣ®зҡ„й–ўж•°гҒ®ж”№е–„гҒҢгҒӘгҒ„е ҙеҗҲгҒҜжҘөеҖӨгҒёеҸҺжқҹгҒ—гҒҹгҒЁгҒҝгҒӘгҒӣгӮӢгҖӮ
дёҠиЁҳгҒ®жүӢз¶ҡгҒҚгҒ«гӮҲгӮӢеҗ„еҸҚеҫ©гҒҜд»ҘдёӢгҒ®гӮҲгҒҶгҒ«иЎЁгҒ•гӮҢгӮӢгҖӮ
йҖЈз¶ҡзҡ„еҫ®еҲҶеҸҜиғҪ й–ўж•° F гҒ§гҒ®еә§жЁҷйҷҚдёӢжі•гҒҜд»ҘдёӢгҒ®жүӢз¶ҡгҒҚгӮ’иЎҢгҒҶ[ 1]
еҲқжңҹгғҷгӮҜгғҲгғ« x
еҸҺжқҹгҒӮгӮӢгҒ„гҒҜеҸҚеҫ©гҒ®дёҠйҷҗеӣһж•°гҒ«йҒ”гҒҷгӮӢгҒҫгҒ§д»ҘдёӢгӮ’еҸҚеҫ©:
1 гҒӢгӮү n гҒ§гҒ®ж·»еӯ— i гӮ’йҒёжҠһгҒҷгӮӢгҖӮгӮ№гғҶгғғгғ—гӮөгӮӨгӮә Оұ гӮ’йҒёжҠһгҒҷгӮӢгҖӮ
xi гӮ’ xi вҲ’ Оұ вҲӮF / вҲӮxi x )
гӮ№гғҶгғғгғ—гӮөгӮӨгӮәгҒ®йҒёжҠһж–№жі•гҒҜгҒ„гҒҸгҒӨгҒӢзҹҘгӮүгӮҢгҒҰгҒҠгӮҠгҖҒеҺіеҜҶгҒ« f (xi ) = F (x )xi гӮ’еӣәе®ҡгҒ—гҒҹдёҠгҒ§ F гҒ®жңҖе°ҸеҢ–пјүгҖҒгҒӮгӮӢгҒ„гҒҜеҸӨе…ёзҡ„гҒӘзӣҙз·ҡжҺўзҙўгҒ§гҒ®йҒёжҠһеҹәжә–гҒ«еҫ“гҒЈгҒҹж–№жі•гҒҢжҢҷгҒ’гӮүгӮҢгӮӢ[ 1]
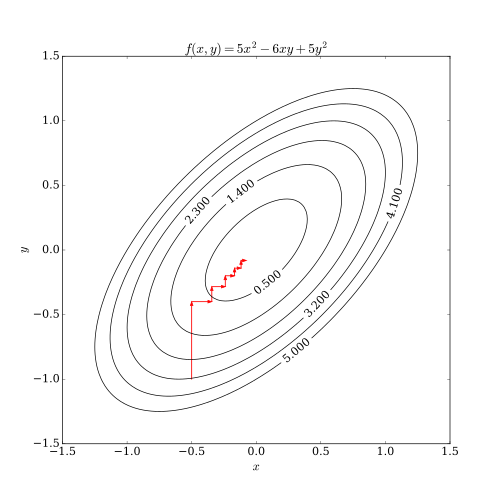
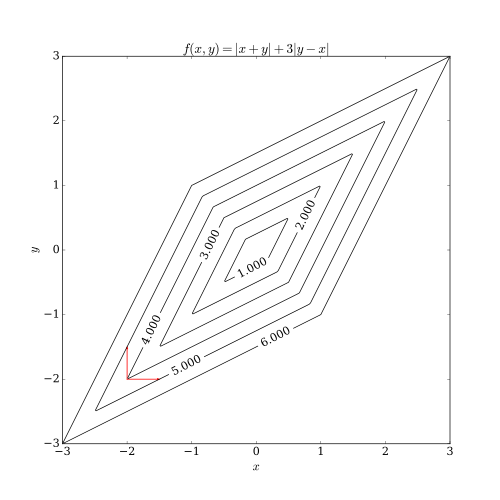
еә§жЁҷйҷҚдёӢжі•гҒҜдәҢгҒӨгҒ®е•ҸйЎҢгӮ’жҠұгҒҲгҒҰгҒ„гӮӢгҖӮдёҖгҒӨзӣ®гҒҜзӣ®зҡ„й–ўж•°гҒҢж»‘гӮүгҒӢгҒӘй–ўж•° гҒ§гҒӘгҒ„е ҙеҗҲгҒ§гҒӮгӮӢгҖӮдёӢиЁҳгҒ®еӣігҒ§гҒҜзӣ®зҡ„й–ўж•°гҒ®зӯүй«ҳз·ҡгҒҢж»‘гӮүгҒӢгҒ§гҒӘгҒ„е ҙеҗҲгҒ«гҒӨгҒ„гҒҰгҖҒеә§жЁҷйҷҚдёӢжі•гҒ®еҗ„еҸҚеҫ©гҒ«гҒҠгҒ„гҒҰеҒңз•ҷзӮ№гҒ§гҒӘгҒ„зӮ№гҒҢжұӮгҒҫгҒЈгҒҰгҒ—гҒҫгҒҶдҫӢгӮ’жҢҷгҒ’гҒҰгҒ„гӮӢгҖӮжңҖе°ҸеҢ–е•ҸйЎҢгҒ«еҜҫгҒ—гҒҰеә§жЁҷйҷҚдёӢжі•гҒ«гҒҠгҒ„гҒҰзҸҫеңЁгҒ®еҸҚеҫ©гҒҢзӮ№ (вҲ’2, вҲ’2) гҒ§гҒӮгӮӢгҒЁгҒҷгӮӢгҒЁгҖҒж¬ЎгҒ®жҺўзҙўж–№еҗ‘гҒЁгҒ—гҒҰиөӨгҒ„зҹўеҚ°гҒ®ж–№еҗ‘гҒ«йҖІгӮҖгҒ“гҒЁгҒҢиҖғгҒҲгӮүгӮҢгӮӢгҒҢгҖҒгҒ©гҒЎгӮүгҒ®ж–№еҗ‘гҒ«йҖІгӮҖгҒ“гҒЁгӮ’иҖғгҒҲгҒҰгӮӮгҖҒгҒ“гҒ®е ҙеҗҲзӣ®зҡ„й–ўж•°гҒҜеў—еӨ§гҒ—гҒҰгҒ—гҒҫгҒҶгҖӮгҒ“гҒ®е ҙеҗҲеә§жЁҷж–№еҗ‘гҒ«йҖІгҒҫгҒҡгҖҒдәҢгҒӨгҒ®жҺўзҙўж–№еҗ‘гӮ’дҪөгҒӣгҒҹж–№еҗ‘гҒ«ж–№еҗ‘гҒ«йҖІгӮҖгҒ“гҒЁгҒ§зӣ®зҡ„й–ўж•°гҒҜж”№е–„гҒ•гӮҢгӮӢгҖӮдёӢиЁҳгҒ®еӣігҒ§гҒҜжңҖйҒ©и§ЈгҒ«еҸҺжқҹгҒ—гҒӘгҒ„дҫӢгӮ’зҙ№д»ӢгҒ—гҒҹгҒҢгҖҒгҒӮгӮӢжқЎд»¶гҒ®дёӢгҒ§гҒҜеҸҺжқҹжҖ§гӮ’зӨәгҒҷгҒ“гҒЁгҒҢгҒ§гҒҚгӮӢ[ 3]
дәҢгҒӨзӣ®гҒ®е•ҸйЎҢзӮ№гҒЁгҒ—гҒҰеә§жЁҷйҷҚдёӢжі•гҒ®дёҰеҲ—еҢ–гҒҢеӣ°йӣЈгҒ§гҒӮгӮӢгҒ“гҒЁгҒҢжҢҷгҒ’гӮүгӮҢгӮӢгҖӮеә§жЁҷйҷҚдёӢжі•гҒ§гҒҜеҗ„еә§жЁҷж–№еҗ‘гҒ«й Ҷз•ӘгҒ«жҺўзҙўгҒ—гҖҒзӣ®зҡ„й–ўж•°гӮ’ж”№е–„гҒҷгӮӢгҒ“гҒЁгҒӢгӮүгҖҒеӨ§иҰҸжЁЎгҒӘдёҰеҲ—еҢ–гҒҜйӣЈгҒ—гҒ„гҒЁгҒ•гӮҢгӮӢгҖӮиҝ‘е№ҙгҒ®з ”究гҒ§еә§жЁҷйҷҚдёӢжі•гҒҜеҗ„еә§жЁҷж–№еҗ‘гҒёгҒ®зӣ®зҡ„й–ўж•°гҒ®еӨүеҢ–гӮ’з·©е’ҢгҒҷгӮӢгҒ“гҒЁгҒ«гӮҲгҒЈгҒҰеӨ§иҰҸжЁЎгҒӘдёҰеҲ—еҢ–гӮ’еҸҜиғҪгҒ«гҒҷгӮӢжүӢжі•гҒҢжҸҗжЎҲгҒ•гӮҢгҒҰгҒ„гӮӢ[ 4] [ 5] [ 6]
еә§жЁҷйҷҚдёӢжі•гҒҜеҚҳзҙ”гҒӘжүӢз¶ҡгҒҚгҒ§е®ҢзөҗгҒҷгӮӢгҒ“гҒЁгҒӢгӮүе®ҹз”ЁйқўгҒ«гҒҠгҒ„гҒҰгҒҜдәәж°—гҒ®гҒӮгӮӢи§Јжі•гҒЁгҒӘгҒЈгҒҰгҒ„гӮӢгҒҢгҖҒжңҖйҒ©еҢ–зҗҶи«–гҒ«й–ўгҒҷгӮӢз ”з©¶иҖ…гҒ®й–“гҒ§гҒҜгӮҲгӮҠиӨҮйӣ‘гҒӘи§Јжі•гӮ’жіЁзӣ®гҒҷгӮӢгҒ“гҒЁгҒҢеӨҡгҒ„гҒ“гҒЁгҒӢгӮүгҖҒгҒ»гҒЁгӮ“гҒ©з ”究гҒ•гӮҢгҒӘгҒ„и§Јжі•гҒЁгҒӘгҒЈгҒҰгҒ„гӮӢ[ 1] [ 7] [ 8] [ 9] [ 10] ж©ҹжў°еӯҰзҝ’ гҒ«гҒҠгҒ‘гӮӢеӨ§иҰҸжЁЎжңҖйҒ©еҢ–е•ҸйЎҢгҒ«еҜҫгҒҷгӮӢеҝңз”ЁгҒ«гҒҠгҒ„гҒҰгӮӮжіЁзӣ®гҒ•гӮҢгӮӢгӮҲгҒҶгҒ«гҒӘгӮҠгҖҒзү№гҒ«гӮөгғқгғјгғҲгғҷгӮҜгӮҝгғјгғһгӮ·гғі гҒ®иЁ“з·ҙжҷӮгӮ„йқһиІ еҖӨиЎҢеҲ—еӣ еӯҗеҲҶи§Ј гҒ«гҒҠгҒ„гҒҰеә§жЁҷйҷҚдёӢжі•гӮ’йҒ©з”ЁгҒ—гҒҹйҡӣгҒ«гҖҒд»–гҒ®и§Јжі•д»ҘдёҠгҒ®е„ӘдҪҚжҖ§гҒҢзӨәгҒ•гӮҢгҒҰгҒ„гӮӢ[ 11] [ 12] [ 13]
^ a b c d Wright, Stephen J. (2015). вҖңCoordinate descent algorithmsвҖқ. Mathematical Programming 151 (1): 3вҖ“34. arXiv :1502.04759 . doi :10.1007/s10107-015-0892-3 .
^ вҖңCoordinate descent вҖқ. Optimization 10-725 / 36-725 . Carnegie Mellon University (2012е№ҙз§Ӣ). 2025е№ҙ3жңҲ10ж—Ҙй–ІиҰ§гҖӮ ^ Spall, J. C. (2012). вҖңCyclic Seesaw Process for Optimization and IdentificationвҖқ. Journal of Optimization Theory and Applications 154 (1): 187вҖ“208. doi :10.1007/s10957-012-0001-1 . ^ Zheng, J.; Saquib, S. S.; Sauer, K.; Bouman, C. A. (2000-10-01). вҖңParallelizable Bayesian tomography algorithms with rapid, guaranteed convergenceвҖқ. IEEE Transactions on Image Processing 9 (10): 1745вҖ“1759. Bibcode : 2000ITIP....9.1745Z . doi :10.1109/83.869186 . ISSN 1057-7149 . PMID 18262913 . ^ Fessler, J. A.; Ficaro, E. P.; Clinthorne, N. H.; Lange, K. (1997-04-01). вҖңGrouped-coordinate ascent algorithms for penalized-likelihood transmission image reconstructionвҖқ. IEEE Transactions on Medical Imaging 16 (2): 166вҖ“175. doi :10.1109/42.563662 . hdl :2027.42/86021 ISSN 0278-0062 . PMID 9101326 . ^ Wang, Xiao; Sabne, Amit; Kisner, Sherman; Raghunathan, Anand; Bouman, Charles; Midkiff, Samuel (2016-01-01). вҖңHigh performance model based image reconstructionвҖқ . Proceedings of the 21st ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming . PPoPP '16. New York, NY, USA: ACM. pp. 2:1вҖ“2:12. doi :10.1145/2851141.2851163 . ISBN 9781450340922 . https://zenodo.org/record/895136 ^ Sauer, Ken; Bouman, Charles (1993-02). вҖңA Local Update Strategy for Iterative Reconstruction from ProjectionsвҖқ . IEEE Transactions on Signal Processing 41 (2): 534вҖ“548. Bibcode : 1993ITSP...41..534S . doi :10.1109/78.193196 . https://engineering.purdue.edu/~bouman/publications/orig-pdf/sp2.pdf . ^ Yu, Zhou; Thibault, Jean-Baptiste; Bouman, Charles; Sauer, Ken; Hsieh, Jiang (2011-01). вҖңFast Model-Based X-ray CT Reconstruction Using Spatially Non-Homogeneous ICD OptimizationвҖқ . IEEE Transactions on Image Processing 20 (1): 161вҖ“175. Bibcode : 2011ITIP...20..161Y . doi :10.1109/TIP.2010.2058811 . PMID 20643609 . https://engineering.purdue.edu/~bouman/publications/orig-pdf/tip28.pdf . ^ Thibault, Jean-Baptiste; Sauer, Ken; Bouman, Charles; Hsieh, Jiang (2007-11). вҖңA Three-Dimensional Statistical Approach to Improved Image Quality for Multi-Slice Helical CTвҖқ . Medical Physics 34 (11): 4526вҖ“4544. Bibcode : 2007MedPh..34.4526T . doi :10.1118/1.2789499 . PMID 18072519 . https://engineering.purdue.edu/~bouman/publications/orig-pdf/medphys1.pdf . ^ Canutescu, AA; Dunbrack, RL (2003). вҖңCyclic coordinate descent: A robotics algorithm for protein loop closure.вҖқ . Protein Science 12 (5): 963вҖ“72. doi :10.1110/ps.0242703 . PMC 2323867 . PMID 12717019 . https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2323867/ . ^ Hsieh, C. J.; Chang, K. W.; Lin, C. J.; Keerthi, S. S.; Sundararajan, S. (2008). вҖңA dual coordinate descent method for large-scale linear SVMвҖқ . Proceedings of the 25th international conference on Machine learning - ICML '08 . pp. 408. doi :10.1145/1390156.1390208 . ISBN 9781605582054 . http://ntu.csie.org/~cjlin/papers/cddual.pdf ^ Hsieh, C. J.; Dhillon, I. S. (2011). Fast coordinate descent methods with variable selection for non-negative matrix factorization (PDF) . Proceedings of the 17th ACM SIGKDD international conference on Knowledge discovery and data mining - KDD '11. p. 1064. doi :10.1145/2020408.2020577 . ISBN 9781450308137 ^ Nesterov, Yurii (2012). вҖңEfficiency of coordinate descent methods on huge-scale optimization problemsвҖқ . SIAM J. Optim. 22 (2): 341вҖ“362. doi :10.1137/100802001 . http://www.ulouvain.be/cps/ucl/doc/core/documents/coredp2010_2web.pdf .
Bezdek, J. C.; Hathaway, R. J.; Howard, R. E.; Wilson, C. A.; Windham, M. P. (1987), вҖңLocal convergence analysis of a grouped variable version of coordinate descentвҖқ, Journal of Optimization Theory and Applications (Kluwer Academic/Plenum Publishers) 54 (3): pp. 471вҖ“477, doi :10.1007/BF00940196 Bertsekas, Dimitri P. (1999). Nonlinear Programming, Second Edition Athena Scientific, Belmont, Massachusetts. ISBN 1-886529-00-0 .
Luo, Zhiquan; Tseng, P. (1992), вҖңOn the convergence of the coordinate descent method for convex differentiable minimizationвҖқ, Journal of Optimization Theory and Applications (Kluwer Academic/Plenum Publishers) 72 (1): pp. 7вҖ“35, doi :10.1007/BF00939948 , hdl :1721.1/3164 Wu, TongTong; Lange, Kenneth (2008), вҖңCoordinate descent algorithms for Lasso penalized regressionвҖқ, The Annals of Applied Statistics (Institute of Mathematical Statistics) 2 (1): pp. 224вҖ“244, arXiv :0803.3876 , doi :10.1214/07-AOAS147 Richtarik, Peter; Takac, Martin (2011-04), вҖңIteration complexity of randomized block-coordinate descent methods for minimizing a composite functionвҖқ, Mathematical Programming (Springer) 144 (1вҖ“2): pp. 1вҖ“38, arXiv :1107.2848 , doi :10.1007/s10107-012-0614-z Richtarik, Peter; Takac, Martin (2012-12), вҖңParallel coordinate descent methods for big data optimizationвҖқ, ArXiv:1212.0873 , arXiv :1212.0873